例谈基于数学核心素养的课堂教学设计——以“基本不等式”为例

金 兰

(浙江省诸暨荣怀学校 浙江 诸暨 311800)

1.背景介绍

必修教材对基本不等式的研究，都是从背景引入、抽象提炼、证明方法、几何意义、变式引申、拓展应用等六个方面进行展开的，既有逻辑推理，又有直观的几何解释，使学生充分运用数形结合的思想方法，进一步培养其抽象概括能力和推理论证能力.是高考经久不衰的热点问题。

2.辨析、认清基本不等式的特征与功能

3.探究、理解基本不等式成立的条件

“一正二定三相等”是教学经验的沉淀，既总结了影响基本不等式成立的三个条件，又概括了应用基本不等式的三个步骤，它们是一个和谐的整体，缺一不可．

3.1 “一正”，基本不等式成立的基础基本不等式的研究对象是两个非负数，即a≥0，b≥0，这是基本不等式成立的基础．

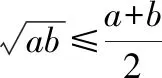
3.3 “三相等”，基本不等式成立的保证。“一正二定”是使用基本不等式的两个重要条件，但如果没有“相等”来做最后保证，只能说是一种形式．因此，“一正二定三相等”是一个和谐的整体，缺一不可，相等就是参与不等式的各个部分相等．

例1：判断下列不等式是否正确

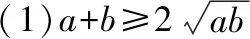
(2)a2+b2>2ab解析：错误；直接举出反例当a=b=0时

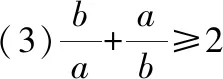
例2:求下列式子的最值

(1)若正数x,y满足x+y=6，求xy的最大值

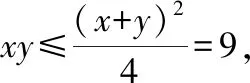
(2)当实数满足a+b=2,则3a+3b的最小值

(3)x>0,y>0, 满足x+4y=40，则lgx+lgy的最大值

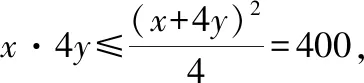
当且仅当时取到最大值2

4.合理构造，创设使用基本不等式的情境

基本不等式的价值在于它的工具性，可以用它来求解许多和最值有关的问题． 然而这些问题往往不是以基本不等式的形式明显地呈现在学生面前的，而是需要经过转化才露出其庐山真面目． 这就要求合理构造，创设使用基本不等式的情境，对学生配凑技能和化归意识都有较高要求．

4.1 用整体代换的方法构造基本不等式。

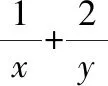
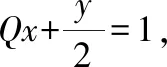
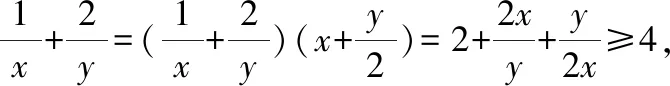
“1 的整体代换”在此类问题中可大显身手；用配凑、换元、消元等方法构造基本不等式

分析：令2x+1=a,y+2=b,则a>0,b>0,a+b=6

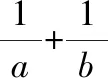
例3的第(2)题对学生来说难度较大，但如果学生能够从本质上理解基本不等式适用于相等关系下双变量的最值问题，就可以大胆换元构造，将陌生问题化归为熟悉模型．

例4:基本不等式在函数中的应用

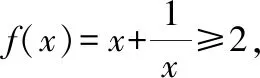
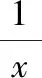
即x=±1时取“=”

解析：基本不等式中，参与不等式的两个变量必须是正数，否则要合理转化为正数．本题定义域为{x|x≠0}，这里习惯性认为x>0,而丢失了x<0的情形.

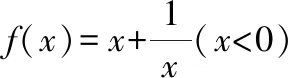
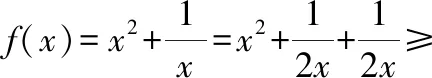
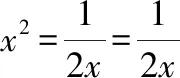
基本不等式应用要反复训练，不断强化。教师要引导学生认真辨析基本不等式的形状和结构特征，探求合适的方法建立不等式，关注不等式成立的条件，体验用不等式解决最值问题的过程，对基本不等式的应用不能只停留在简单的表面，教学中要重视结构特征，让基本不等式在创造与拓展中发挥功能，从而不断提升数学素养。