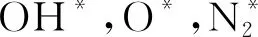水中介质阻挡放电空气等离子体的放电特性
2019-06-03周玉超岑祥旗孙兆杰彭新志
周玉超,洪 义,岑祥旗,孙 韬,孙兆杰,彭新志
(大连民族大学 物理与材料工程学院,辽宁 大连 116600)
近年来,介质阻挡放电等离子体技术作为一种行之有效的高级氧化技术,在水中有机污染物的降解方面受到了国内外的广泛关注[1-3]. 介质阻挡放电相比于电晕放电、火花放电、弧光放电具有放电稳定、均匀、弥散,电子密度和能量高,电极寿命长以及避免回路漏电等优点[2]. 介质阻挡放电过程中产生的紫外光、冲击波、高能电子、活性粒子(如OH*,O*,H*,H2O2,O3)能够使水中有机污染物发生断键、开环、取代等一系列反应,使其变成小分子安全物质,乃至最终将其去除[4]. 目前,已报道的水中介质阻挡放电处理有机污染物装置的特点是等离子体产生在浸没于水中的反应器内部,并且活性粒子需要通过一定距离的传输后,再以鼓泡/曝气的形式与水中有机污染物反应[5-7]. 在这种条件下,大部分的活性粒子由于辐射寿命非常短暂(只有几十ns),因此与水中有机污染物反应之前早已消失,这将降低处理效率.
基于上述原因,本文采用针-板式电极结构在水中直接产生了介质阻挡放电空气等离子体,并对其进行了电气特性和光谱诊断,确定了相应的电气参量和等离子体参量.
1 实验装置
图1为针-板式水中介质阻挡放电等离子体发生装置的结构. 装置的高压电极为外径2 mm、内径1.8 mm、长250 mm的不锈钢钢管,并与频率为8 kHz的交流高压电源相连. 为了预先产生种子电荷和防止高压电极与水接触,把高压电极插入到外径3 mm、内径2 mm、长200 mm的石英玻璃管,并且高压电极放电端距石英玻璃管开放端的距离为3 mm. 低压电极为长40 mm、宽50 mm、厚0.3 mm的铜箔,其上方覆盖着长50 mm、宽50 mm、厚1 mm 的石英玻璃板. 石英玻璃板与外径32 mm、内径30 mm、高70 mm的圆柱形石英玻璃管组成盛水的石英容器. 放电采用的水为自来水,高压电极放置在距石英玻璃板10 mm的位置.
工作气体空气由高压电极进入,并利用质量流量计控制其流量为2 L/min. 电源采用幅值为0~20 kV、频率为8 kHz的交流电源. 利用Textronix P6015A高压探头测量电源输出电压,通过测量与接地电极串联的20 Ω电阻上的电压得到输出电流,通过与接地电极串联1 μF电容得到李萨如图形,并记录在Tektronix MDO3012示波器上. 由光谱仪(Acton Research Spectrapro-2500i)选择300 mm-1光栅(300~900 nm)、2 400 mm-1光栅(OH:306~312 nm,Hα:656.3 nm)以及狭缝宽度20 μm采集特征发射光谱. 光纤探头固定在距石英玻璃板和圆柱形石英玻璃分别3 mm和2 mm处. 由佳能数码相机EOS 5D Mark Ⅲ拍照得到放电照片(图2).
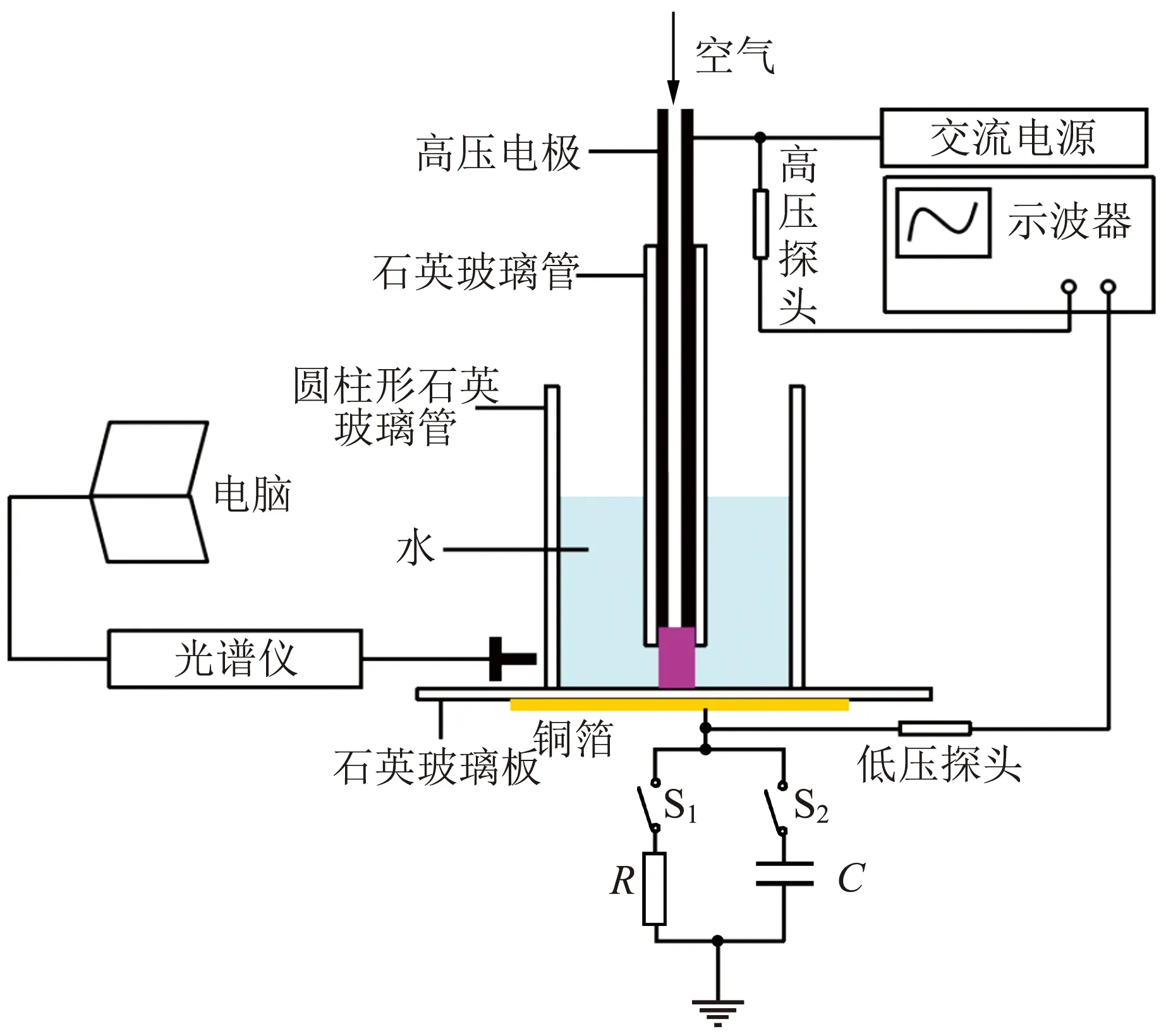
图1 针-板式水中介质阻挡放电等离子体发生装置的结构

图2 峰值电压为13.5 kV时的放电照片
2 结果与讨论
2.1 电气特性诊断
图3为针-板式水中介质阻挡放电空气等离子体装置的等效电路图,Cd表示高压电极与接地电极之间的介质电容,Cp和Rp分别表示空气等离子体的气隙电容和等效电阻,Utot(t)为施加在等离子体装置上的工作电压,Itot(t)为通过等离子体装置的总电流,Idc(t)为通过高压电极和接地电极之间气隙的传导电流,Idp(t)为通过石英玻璃板介质的位移电流.
根据基尔霍夫定律,从图3中可得到
(1)
Itot(t)=Idp(t)+Idc(t).
(2)
从式(1)中可以看出,只要确定介质电容Cd,就可根据测量得到的电压波形计算出任意工作电压所对应的位移电流Idp(t),通过式(2)由测量的总电流减去位移电流可得到传导电流Idc(t). 实验中发现,当峰值电压为2.5 kV时,装置没有出现放电现象,因此示波器记录的电流为位移电流,把位移电流代入到式(1)即可计算出介质电容Cd值.
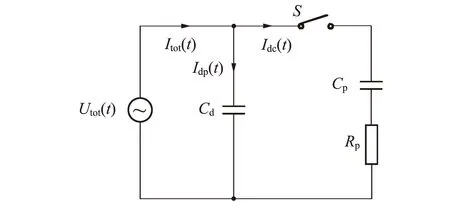
图3 空气等离子体装置的等效电路
图4给出了峰值电压为2.5 kV时的电压和电流波形. 从图4中可以看出,电流波形为正弦波形,并且波形上没有出现电流脉冲,说明峰值电压为2.5 kV时电极间没有发生放电现象,因此测量得到的电流为位移电流.
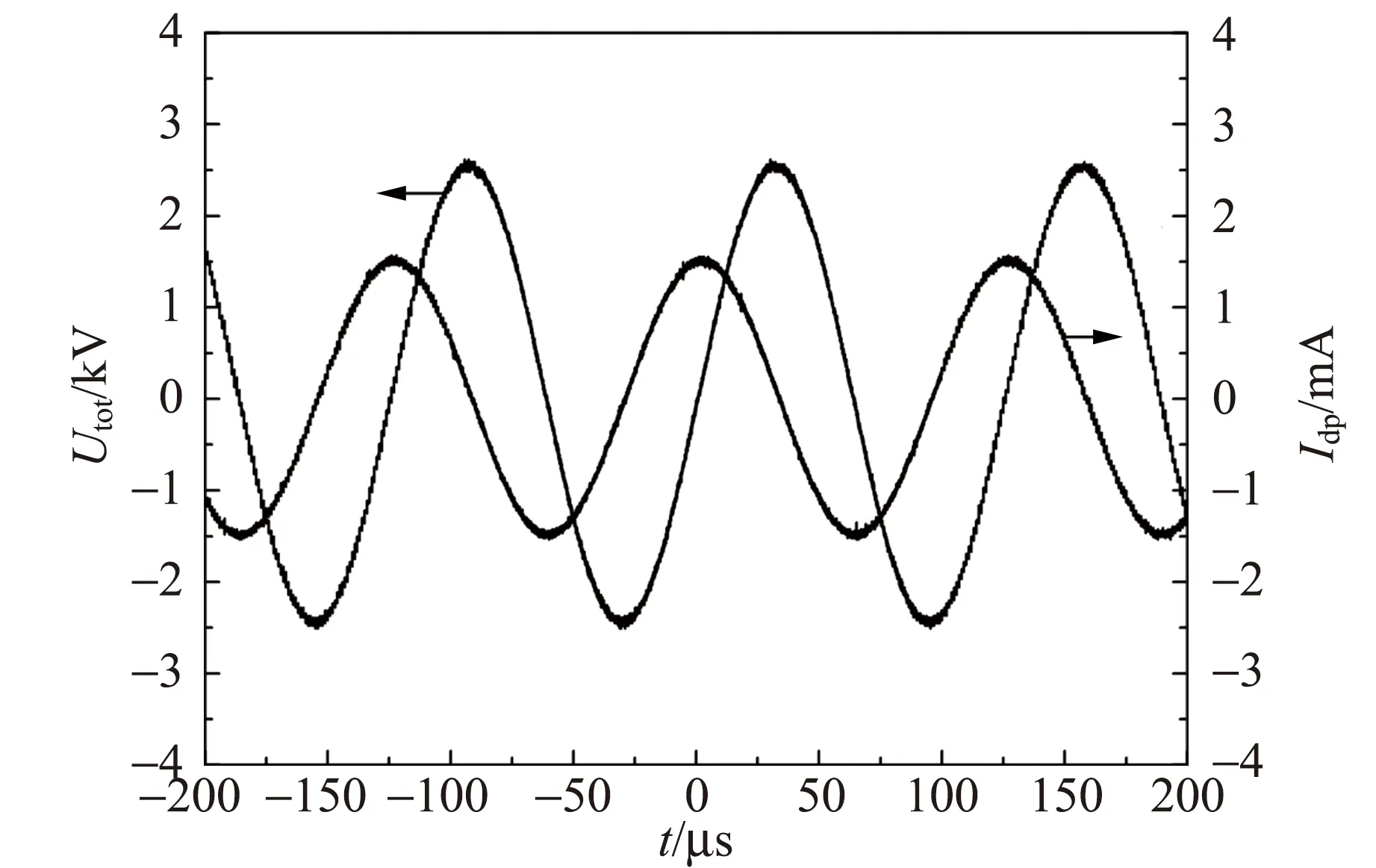
图4 峰值电压为2.5 kV时的工作电压和位移电流波形
图5给出了3个放电周期内介质电容Cd值的变化.
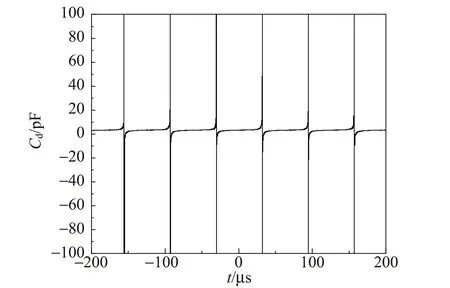
图5 3个放电周期内介质电容Cd值的变化
从图5中可以看出,介质电容Cd值在每半个放电周期出现2个极大值,这是因为分母过零点导致的. 除去极大值,并对介质电容Cd取平均,其值为3.29 pF.
图6~7给出了峰值电压为13.5 kV时的工作电压、总电流、传导电流以及位移电流的波形. 可以看出,每半个放电周期传导电流波形上出现了大量的电流脉冲,说明放电过程中电极间出现了大量的微放电通道,并且与已报道的大气压介质阻挡放电的典型电压-电流波形一致[8]. 位移电流远小于传导电流,说明放电过程中注入的功率大部分用于产生空气等离子体. 总电流的正负峰值分别为232.52 mA和-51.20 mA,而传导电流的正负峰值分别为224.05 mA和-43.56 mA.
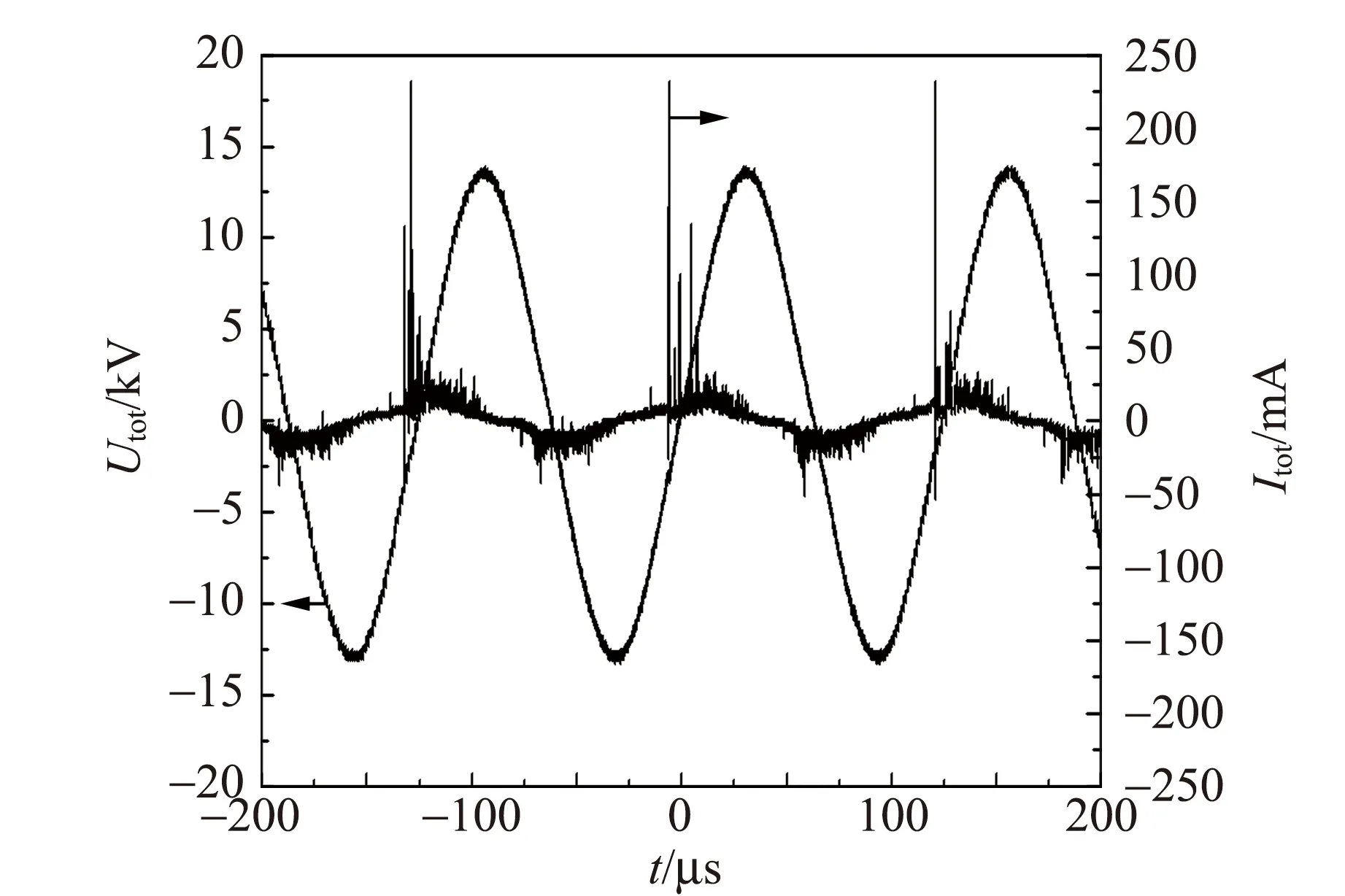
图6 峰值电压为13.5 kV时工作电压和总电流的波形
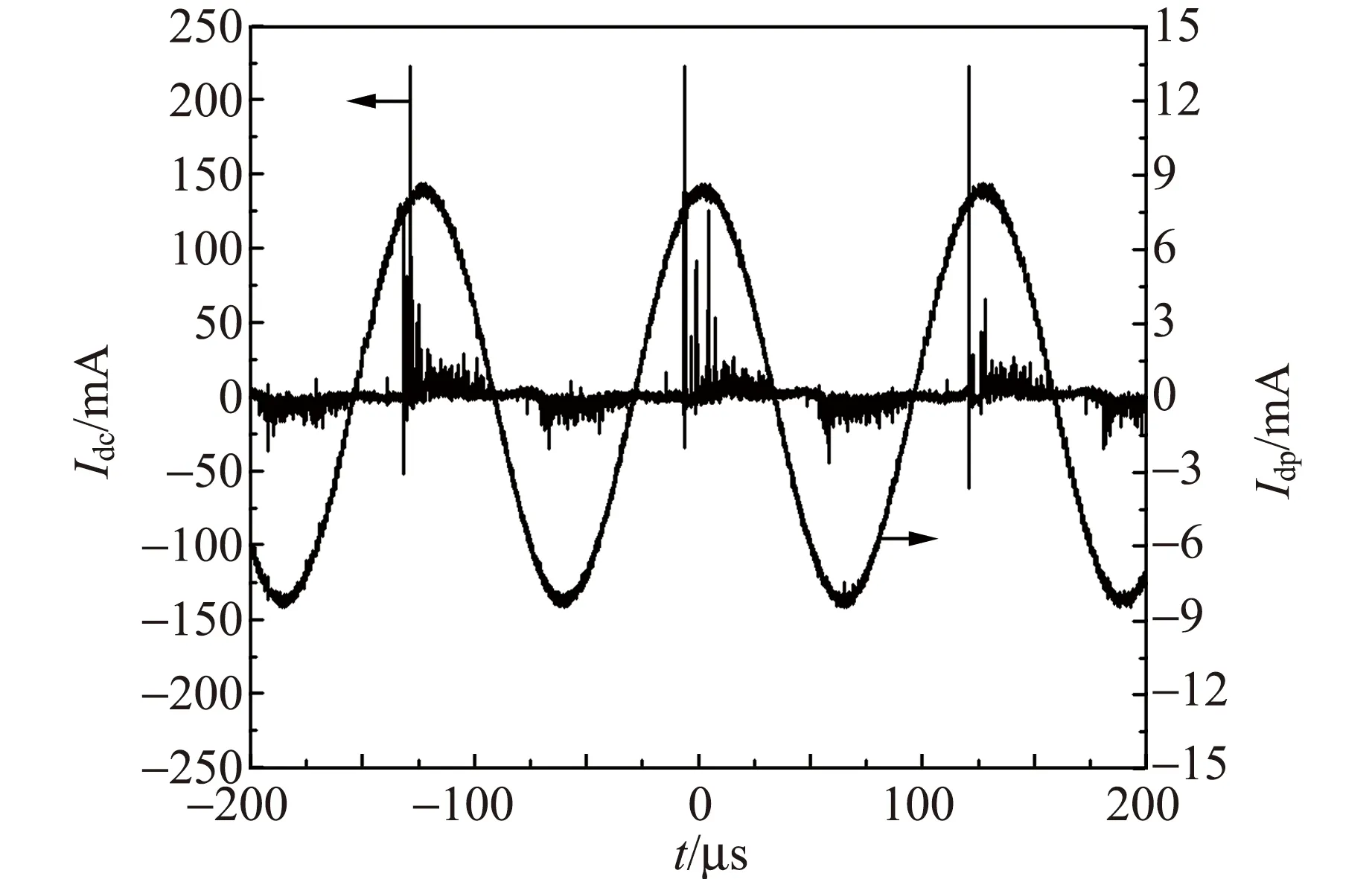
图7 峰值电压为13.5 kV时传导电流和位移电流的波形
图8给出了放电过程中的有效功率随峰值电压的变化. 通过求李萨如图形的面积计算得到有效功率. 从图8可以看出,有效功率随峰值电压的增大,几乎线性地增大. 当峰值电压从12 kV增大到15 kV时,有效功率从16.22 W增大到了29.28 W.

图8 有效功率随峰值电压的变化
2.2 等离子体参量诊断
图9给出了峰值电压为12.5 kV时250~900 nm波长范围的发射光谱.

(a)250~550 nm
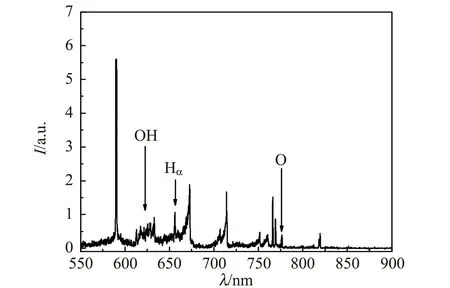
(b)550~900 nm图9 峰值电压为12.5 kV时的发射光谱
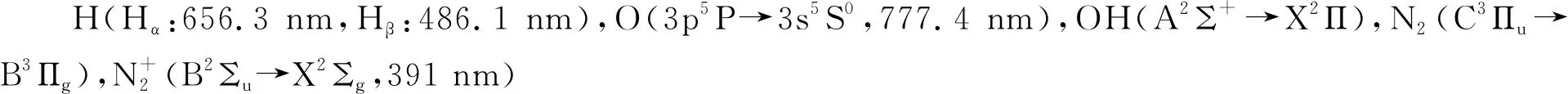
图10为气体温度随峰值电压的变化,从图10可看出,当峰值电压从12 kV增大到15 kV时,气体温度从728 K增大到了843 K.

图10 气体温度随峰值电压的变化
图11为OH(A2Σ+→X2Π,Δν=0)从306~312 nm跃迁产生分子谱带的实验测量光谱和理论模拟光谱,由图11进行比较确定气体温度[9].

图11 OH谱带的实验测量光谱和理论模拟光谱
图12为电子密度随峰值电压的变化,图13为峰值电压为14 kV时的Hα谱线的佛克托线型拟合. Hα谱线的线型展宽是由多普勒展宽(ΔλD)和仪器展宽(Δλinst)引起的高斯线型展宽(ΔλG)、由斯塔克展宽(ΔλS)和范德瓦尔斯展宽(ΔλV)引起的洛伦兹线型展宽ΔλL的卷积,即佛克托线型展宽. 因此,斯塔克展宽[10]可以从Hα谱线的佛克托线型展宽中分离出其他展宽得到,并利用
(3)
可得到电子密度ne.
在大气压等离子体中,原子发射谱线的斯塔克展宽是由于电子与激发态原子之间发生碰撞,导致原子的激发态能级产生展宽和位移(斯塔克效应)引起的. 从式(3)中可以看出,电子密度越大,Hα谱线的斯塔克展宽越大. 利用He-Ne激光器(625.3 nm)校正光谱仪,通过高斯函数拟合得到仪器展宽(Δλinst),其值为0.06 nm.
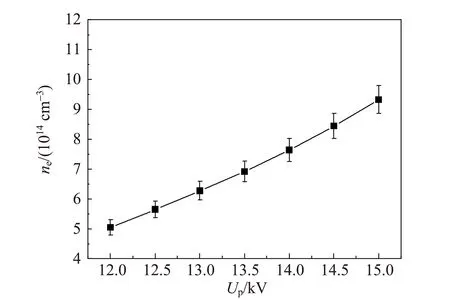
图12 电子密度随峰值电压的变化
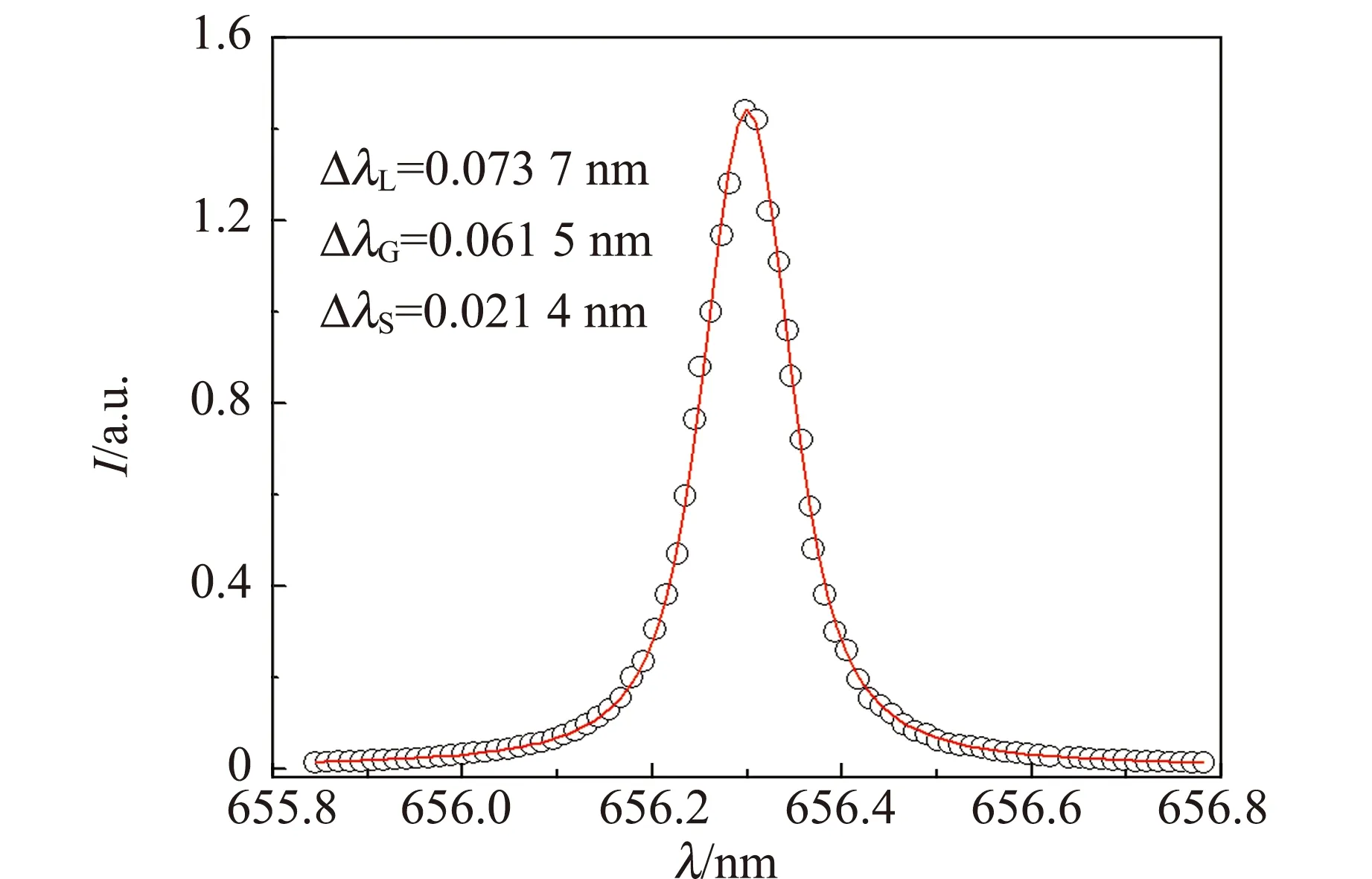
图13 峰值电压为14 kV时Hα谱线的佛克托线型拟合
多普勒展宽[8]由
(4)
计算得到,式中Tg为气体温度(从图10中得到),M为氢原子质量,λ0为Hα谱线的波长.
范德瓦尔斯展宽[8]可由
ΔλV=5.736/Tg0.7
(5)
得到.
从图12中可以看出,电子密度随峰值电压几乎是线性地增大,并且当峰值电压从12 kV增大到15 kV时,电子密度从 5.05×1014cm-3增大到了9.33×1014cm-3.
3 结 论