法布里-珀罗干涉仪测平板玻璃折射率的方法研究
2019-06-03严琪琪许怀哲
严琪琪,唐 芳,沈 嵘,许怀哲,李 华
(北京航空航天大学 物理科学与核能工程学院,北京 100083)
法布里-珀罗(Fabry-Perot,F-P)干涉仪是利用分振幅的多光束干涉原理而设计的精密测量仪器,光束经该仪器所形成的干涉图样和双光束干涉形成的干涉图样相比,干涉条纹更加清晰明锐,分辨率更高,所以它在光谱的精细结构[1]、精确测量光波波长[2-3]和激光谐振腔的研究[4]等方面都有重要的应用. 光学玻璃的折射率是保证其所在光学系统成像质量的基础,准确测量光学玻璃的折射率在其各自研究领域都具有现实的应用意义[5].
光学玻璃折射率的测量方法主要有测角法[6-10]和干涉法[11-16]. 测角法对被测光学玻璃的形状有较严格的要求,一般用来测量棱镜折射率;而干涉法的应用相对较灵活,它主要集中在测量平板玻璃的折射率上. 目前,对平板玻璃折射率的测量方法主要有迈克耳孙干涉法[14-16]和分光仪形成的多光束干涉法[12-13],然而用分光仪测量平板玻璃的折射率时,干涉条纹的可见度很难保证,且干涉级次越高干涉条纹越暗,甚至不能从望远镜中观察到.
本文根据F-P干涉仪的干涉原理,提出了原理简单、操作简便、测量准确的测平板透明材料折射率的多光束干涉实验方法,并对在F-P干涉仪中插入平板玻璃前、后所产生的相邻干涉亮纹直径平方的差值进行了理论分析. 实验测量结果和理论分析完全吻合;而且该理论分析结果也能够有效地解释迈克耳孙干涉仪测折射率时的异常现象研究[16]中观察到的当在迈克耳孙干涉仪的1个臂上插入平板玻璃后,平板玻璃似乎会导致其所在光路光程变小的“反直观”现象.
1 F-P干涉仪的结构及其干涉原理
1.1 F-P干涉仪的结构
F-P干涉仪的核心是由2块内表面相互平行的平面玻璃板或石英板组成的,且在其相对的2个面上都镀有平整度很高的高反射率的反射膜. 一般为了消除两平板相背平面上反射光的影响,平行板的外表面会有很小的楔角,其结构如图1所示.
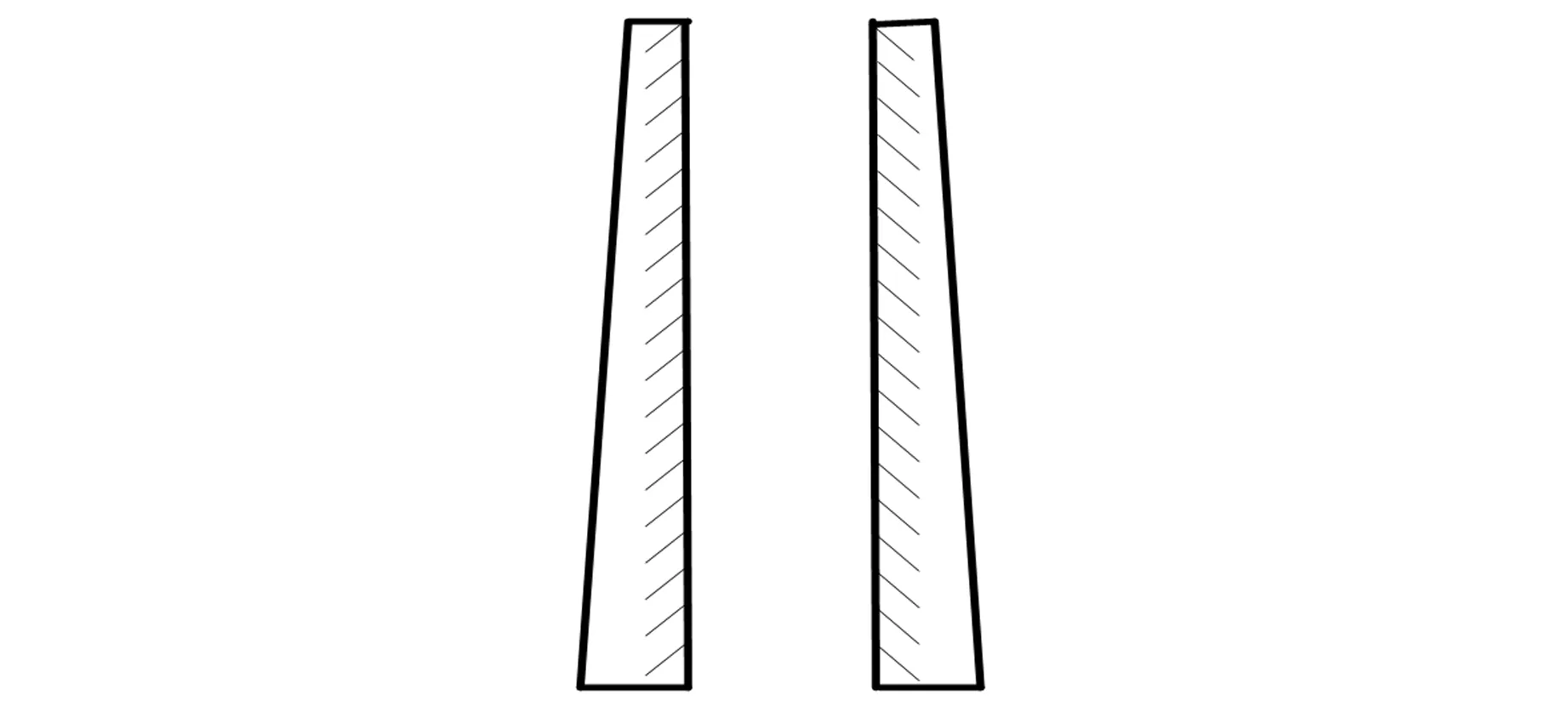
图1 F-P干涉仪的核心部件
1.2 F-P干涉仪的干涉原理及光程分析
F-P干涉仪的干涉原理如图2所示. 自扩展光源上任一点发出的光束入射到镀有高反射率反射膜的平面上后,光就在两者之间多次往返反射,最后构成多束平行的透射光和多束平行的反射光. 在这2组光中,相邻2束光之间的光程差都相等,但振幅在不断衰减. 以其中1组透射光进行分析,这组平行光经会聚透镜后,在其后焦面上可产生形状为同心圆的等倾干涉条纹,倾角相同的光线对应的干涉条纹的干涉级数相同.
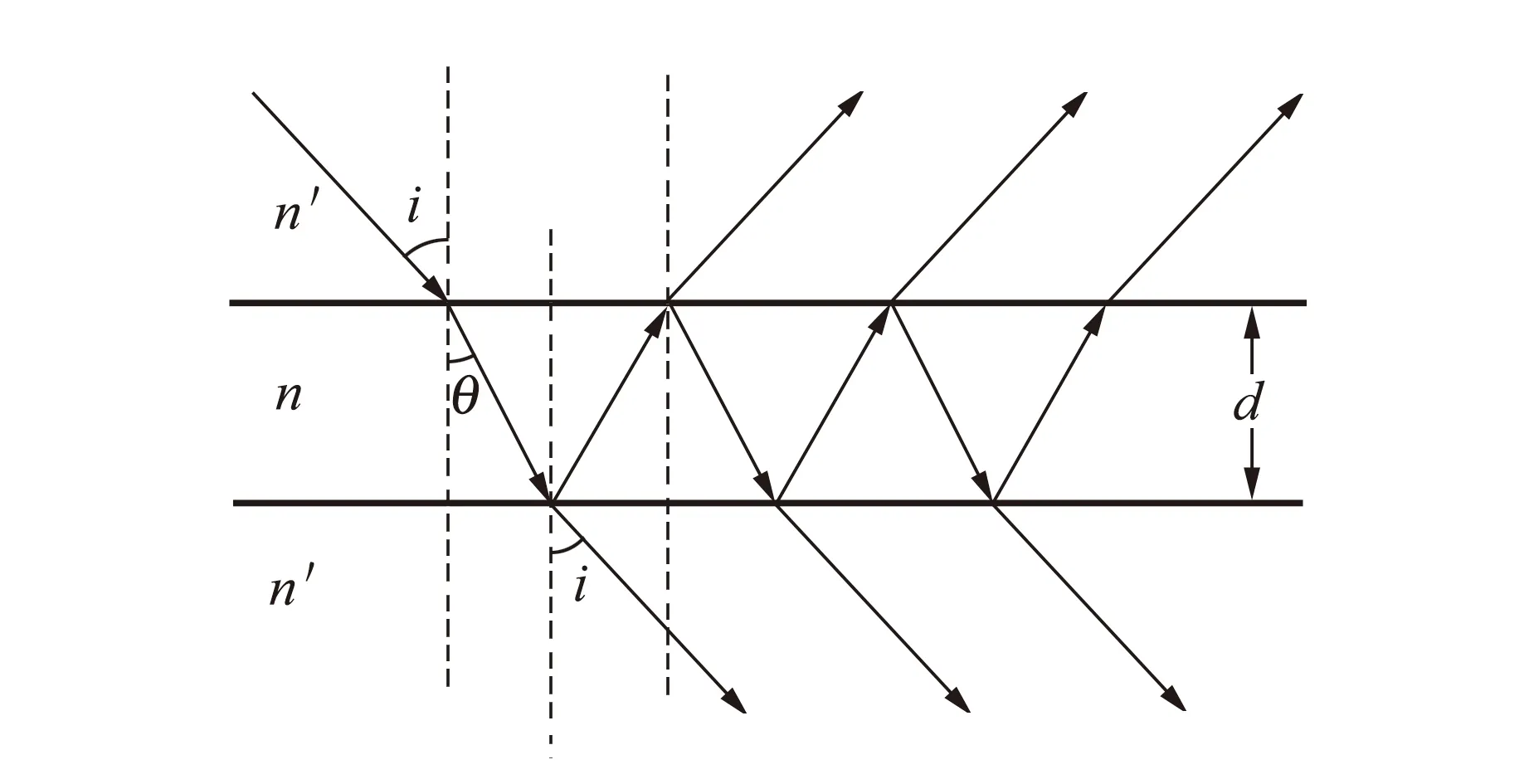
图2 表面平行的介质层中光的反射和折射
设F-P干涉仪外部介质折射率为n′,内部介质折射率为n且n>n′,光线入射角为i,进入内部介质的折射角为θ,两平行板间的间距为d,则透射光中相邻两光束之间的光程差ΔL为
ΔL=2ndcosθ.
(1)
由光的干涉可知,干涉为亮纹时,
2ndcosθk=(k+e)λ,
(2)
其中,λ为入射光波长,k为等倾干涉条纹最里面亮纹的整数序,e<1为中心不完整干涉亮纹的小数序.
当光线垂直入射时,θk=0,则有
2nd=(k+e)λ.
(3)
设从中心数起,第p个干涉亮纹的角半径为θp,干涉序为kp,则有
2ndcosθp=kpλ=(k-p+1)λ.
(4)
若θp很小,则有
(5)
若用焦距为f的凸透镜测量等倾干涉圆环的直径Dp,则有
(6)
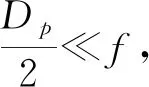
(7)
由折射定律,可知
(8)
由式(3)~(8)可得从中心数起,第p个干涉亮纹直径的平方为
(9)
由式(9)可得相邻两干涉亮纹直径平方的差应为
(10)
1.3 插入平板玻璃后的光程变化分析
保持1.2部分的干涉装置不变,把厚度为t、折射率为n1的平板玻璃平行地插入到两反射面之间,光线进入平板玻璃的折射角为θ′. 其透射光的光路如图3所示,则透射光中相邻两光束之间的光程差ΔL′为
ΔL′=2n(d-t)cosθ+2n1tcosθ′.
(11)
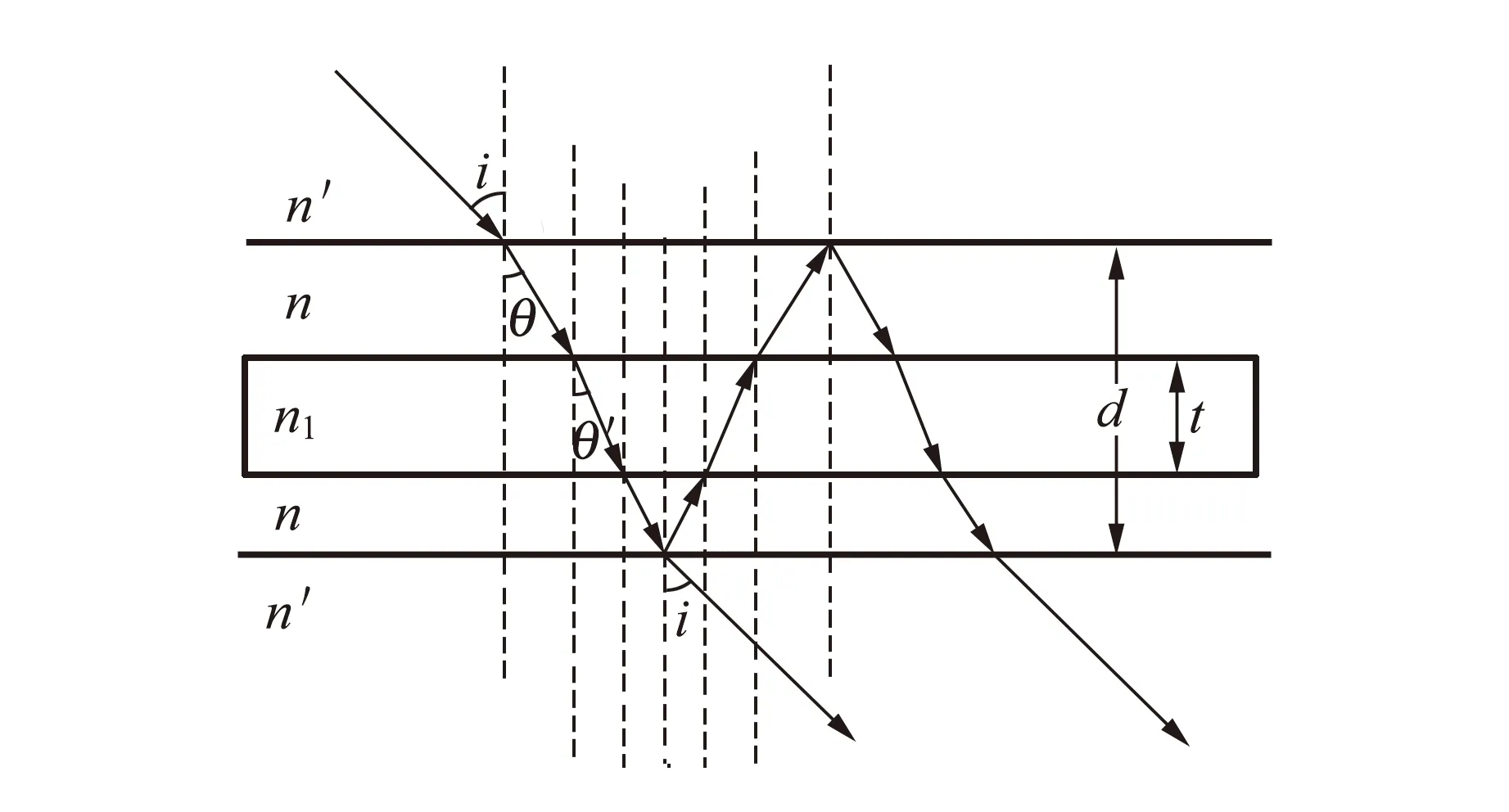
图3 插入平板玻璃后的相邻2束透射光的光路图
采用1.2部分的分析方法,可得插入平板玻璃后, 从中心数起第q个干涉亮纹直径的平方为
(12)
由式(12)可得插入平板玻璃后相邻两干涉亮纹直径的平方差应为
(13)
对比式(10)和式(13)可以看出,若F-P干涉仪放置在空气中,即n=n′=1,则当在两反射面间平行地插入平板玻璃(n1>1)后,相邻两干涉亮纹直径的平方差将会变大. 根据插入平板玻璃前、后相邻干涉亮纹直径的平方差的变化即可得出该平板玻璃折射率n1的值.
2 实验设计及数据测量处理
2.1 实验光路的设计
由式(10)和式(13)可知,在n=n′=1、入射光波长λ、透镜焦距f和平板玻璃厚度t已知的情况下,可以首先通过移测显微镜测出干涉亮纹的直径,进而得到两反射面之间的间距d;保持间距d不变,平行插入平板玻璃,再次通过移测显微镜测出此时干涉亮纹的直径,即可得到所要测平板玻璃的折射率n1. 其测量光路如图4所示.

图4 干涉亮纹直径测量光路图
2.2 实验数据测量及处理
实验中所用激光波长λ=632.8 nm,透镜焦距f=150 mm,平板玻璃厚度t=1.956 mm,空气折射率n=n′=1.
当放置在空气中的F-P干涉仪中间没插入待测平板玻璃时,干涉亮纹直径的测量数据如表1所示,其中x为移测显微镜示数,D为干涉圆环的直径.

表1 无玻璃放入时,干涉亮纹直径的测量数据
由于干涉条纹的确切序数k′无法知道,可令k′=k-i,i是为测量方便规定的干涉条纹序,则
(14)
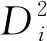
保持F-P干涉仪d不变,中间插入待测平板玻璃时干涉亮纹直径的测量数据如表2所示,表中,x为移测显微镜示数,D为干涉圆环的直径.

表2 平板玻璃放入后,干涉亮纹直径的测量数据
采用与未放入平板玻璃时相同的数据处理方法,可得线性相关系数r=0.999 93→1,
(15)
因t=1.956 mm,d=5.189 2 mm,由式(15)可得n1=1.494.
通过观察实验现象可以发现,当在置于空气中的F-P干涉仪2个反射面中间插入平板玻璃后,相邻2条干涉亮纹之间的间距变大了,如图5所示,两图中的十字叉丝均放置在从中心向右数第6条干涉条纹所在的位置. 该实验现象与理论分析所得插入平板玻璃后相邻干涉条纹直径平方的差值和所插入介质折射率之间关系的表达式(13)相吻合.
为验证理论分析的正确性,分别对不同厚度的平板玻璃进行多次测量,均可得到n1→1.5的结果,同时可观察到与图5(a)和(b)对比变化趋势相同的实验现象. 由此可见,利用上述分析方法和实验装置测平板玻璃的折射率切实可行.

(a)未插入玻璃时

(b)插入玻璃后图5 干涉图样
3 结束语
通过理论分析给出了适用于F-P干涉仪来实现分振幅多光束干涉的相邻干涉条纹直径平方的差值为一定值的普适公式. 实验数据的测量结果和理论分析得到的普适公式相吻合,且该理论分析结果也能够有效地解释迈克耳孙干涉仪测折射率时的异常现象研究[16]中观察到的所谓“异常”现象.
