舰炮供弹系统动力学仿真分析

葛胜利

(中国船舶重工集团公司第七一三研究所，河南 郑州 450015)

0 引 言

传统舰炮设计理论对舰炮的运动和受力进行分析时，多基于“平面、对称及静平衡”3个基本假设[1]。因此，在对舰炮进行建模与分析时，虽然引入了多种经验系数，但仿真结果与实际仍有较大差异。出现上述现象的原因在于，传统的分析方法实际上是准静态的分析方法，而舰炮实际工作时，是一个受冲击的过程，应采用多体系统动力学的方法进行分析。随着现代火炮设计理论与方法的发展，基于虚拟样机技术的设计越来越受到重视，是未来火炮设计理论与方法的发展趋势。例如美国TACOM公司提出利用虚拟样机技术支持3 200多种武器系统的研制，依据武器系统的虚拟样机可以在物理样机制造之前，全面掌握武器潜在的各种问题，提出设计变更和设计反馈，减少设计失误和实物试验验证次数。

虚拟样机技术是一种新型的产品设计和过程开发的方法，虚拟样机模型包含了产品全寿命周期设计的信息，包括物理样机的几何信息、材料信息和供仿真分析的数学模型信息，这种模型实际上是一种设计、分析一体化的模型，可用来分析和评估系统的性能，为物理样机的设计和制造提供参考依据。虚拟样机开发过程如图1所示。

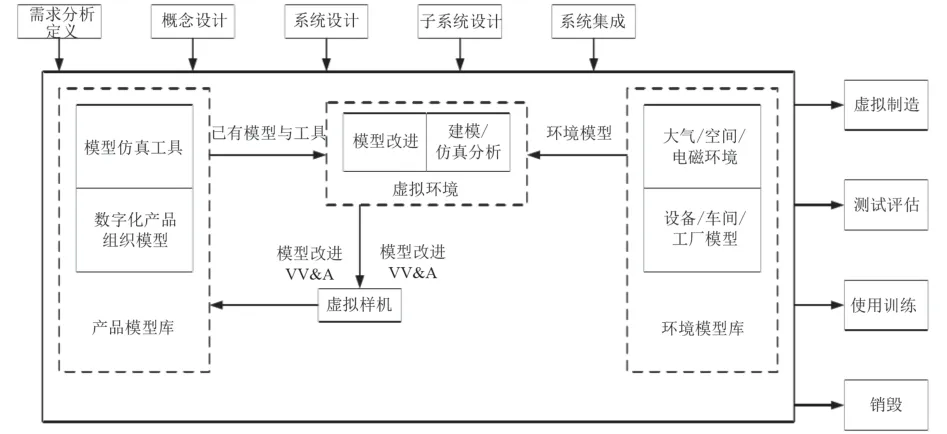
图1 虚拟样机开发过程Fig.1 Virtual prototype development process

建立一个全面反映舰炮的工作过程并准确描述各零部件运动和受力的动力学模型，是解决舰炮仿真问题的重要步骤。虚拟样机技术是将机械系统作为一个整体进行考虑，外部影响通过作用力和驱动约束等元素施加于系统，可以准确地分析系统内部构件之间的关系与作用[2]。本文探讨了虚拟样机技术在某舰炮供弹系统设计中的应用，通过在PRO/E环境下建立的三维参数化模型，在ADAMS中建立供弹系统的虚拟样机模型，并进行动力学仿真研究，得到主要传动件的动力学数据。然后利用已经建立的弹鼓运动阻力参数检测装置对供弹系统样机进行了试验，通过该装置的数据采集系统，输出射击状态下弹鼓运动速度、输入扭矩等参数曲线，其变化趋势及最终状态与仿真计算数据基本吻合，充分证明了计算结果的可信性。

1 供弹系统工作原理

某型舰炮的弹鼓式无链供弹系统是1套大容量、能够连续快速供弹、结构紧凑并具有多弹种更换功能的系统平台，其机械结构简图如图2所示。

供弹系统动力由自动机提供，经过齿轮箱中4级齿轮和太阳轮运动传递至行星轮，行星轮的公转带动内鼓旋转将炮弹从内鼓输出，经齿轮箱各级拨弹轮输入炮膛。

图2 供弹系统结构简图Fig.2 Schematic diagram of the structure of a projectile supply system

2 建立供弹系统虚拟样机模型

本文利用PRO/E软件建立模型，根据供弹系统机械结构，建立三维模型。在PRO/E中装配时，要检查装配模型的干涉情况，以减小仿真分析时，由模型初始状态所引起的误差。弹药传递过程中存在复杂的接触碰撞关系，仿真不但要求得到机构的运动规律，还要能够得到运动过程中零件间的相互作用，以更好的模拟零件的真实工作状态。对于建好的三维模型，首先需要对模型进行校核，检查装配模型是否存在干涉，若存在需对模型进行局部修改或者重新装配，其次在建立动力学模型过程中需对模型进行适当的简化处理，如一些不影响仿真结果的零件（如螺栓、螺母等）和一些不关心的部件（如机箱），可直接删除，这样可以降低求解资源、节省计算时间。

该模型全面反映了机构的几何特征，包括各部分的尺寸、各几何体之间的连接关系和装配关系。

建立模型的步骤如下：

1）在PRO/E中装配好三维实体模型后，将模型导入ADAMS中；

2）在ADAMS中设置重力在-Y方向，并设置每个部件的密度，使其具有转动惯量[4]。

3）机架以及不参加运动的部件和大地建立固定副，齿轮添加转动副。两齿之间添加接触副，接触参数设置为：k=1.1×10E9，e=1.5，δ=45，C=0.01。设置转动副和接触副摩擦系数；并通过软件检查机构自由度验证动力学模型的可解性，对模型中的过约束进行修改。添加完约束必须进行机构检查（model verify），必须确保没有过约束，否则仿真会产生不可预料的结果。特别对于封闭机构（如曲柄滑块机构），ADAMS一定会产生过约束，此时要用基本约束副代替旋转副或滑动副。

4）根据实际试验中自动机射速，在输入轴上施加转速驱动。模拟转速曲线如图3所示。

将实验得到的每2发弹发射间隔转换为星形体的转速，将转速添加在底部曲柄连杆机构的大锥齿轮上，从而给整个机构提供动力。由于实验中每两发弹发射间隔时间是变化的，故需将转速数据导入到ADAMS中，用AKIMA插值拟合发进行拟合，得到曲线，并将转速曲线加载到锥齿轮上，由锥齿轮带动星形体运动，同时锥齿轮与五齿齿轮啮合，带动拨弹轴运动，从而给拨弹轮传递动力。供弹系统的虚拟样机模型如图4所示。

图3 模拟转速曲线Fig.3 Simulated rotational speed curve

图4 弹鼓虚拟样机模型Fig.4 Virtual prototype model of missile and drum

5）仿真计算

建好虚拟样机模型后，选择求解器并确定分析时间及步长，即可进行仿真计算。

3 动力学仿真分析

本文主要分析舰炮发射过程中，从启动到运行平稳这个阶段，考虑了弹鼓中不装弹空载和装满弹满载2种情况。内鼓转动速度决定了供弹系统的供弹速度，进而影响自动机发射率。这段时间内弹鼓旋转角速度和角加速度变化情况如图5和图6所示。

整个过程处于加速阶段，因此齿轮上的作用力较大。运动经由齿轮箱最后一级齿轮与太阳轮的啮合传入弹鼓，此处处于传动链的中间位置。本文采集此处的啮合力曲线如图7所示。

图5 2种情况下弹鼓角速度Fig.5 Projectile angular velocity in two cases

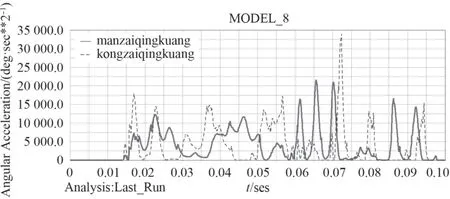
图6 2种情况下弹鼓角加速度Fig.6 The acceleration of the blast angle in two cases

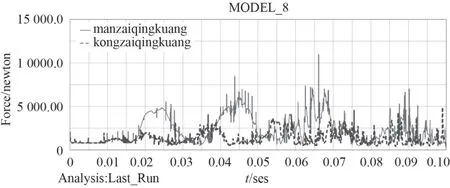
图7 啮合力曲线Fig.7 Meshing force curve

供弹系统启动加速过程中，扭转力矩迅速增大，随着启动过程结束，供弹系统旋转速率稳定，扭转力矩经历正弦式波动后逐渐趋于平缓，最后围绕一个较小值在小范围内正弦波动。如图8所示。

图8 弹鼓启动力矩Fig.8 Start torque of a drum

图5中弹鼓角速度增加基本一致，但满载情况下上升较为平缓，空载情况下曲线出现尖点拐点。从图6中可以看出，空载情况下的弹鼓角加速度变化剧烈，满载情况下较为稳定，同时印证空载情况下受力波动较大。空载时，角加速度最大值出现在0.072 s附近，满载时在0.06—0.07 s内连续出现3次峰值。此时啮合力在7 000 N附近波动，并在0.066 s出现最大值。在0.095 s后，角加速度趋于0，角速度达到最大值，运行趋于平稳。由图7可以看出，空载情况下，受力波动较大，这时轮齿受到较严重的冲击。在速度达到最大值并将稳定运行时，啮合力仍以较大幅度波动，末端反而出现一个最大受力。满载情况下，受力波动较小，但是受力较大，最大值接近11 000 N。在速度达到最大值并稳定运行时，受力逐渐减小趋于稳定。由图8可以看出弹鼓启动力矩最大值为125 N·m，射速稳定后输入扭矩25 N·m。

4 试验验证

弹鼓运动阻力检测装置主要用于研制内能源转管自动机带动弹鼓供弹系统的能源匹配试验、弹鼓运动阻力矩检验和可靠性试验，可以进行模拟试验和动态特性的测试，确定弹鼓供弹系统的阻力距特性、供弹的可靠性以及其他特性，为该产品的检验提供试验数据和技术参数。弹鼓运动阻力检测装置主要由弹鼓阻力矩及运动状态测试系统、弹鼓运动控制系统、炮弹运动及加速度存储测试系统、数据采集及分析系统等4部分组成，如图9所示。

图9 弹鼓运动阻力检测装置Fig.9 Resistance detection device for drums and drums

按照4 200发/min射速设置试验装置状态，弹鼓运动角速度曲线如图10所示，输入扭矩曲线如图11所示。

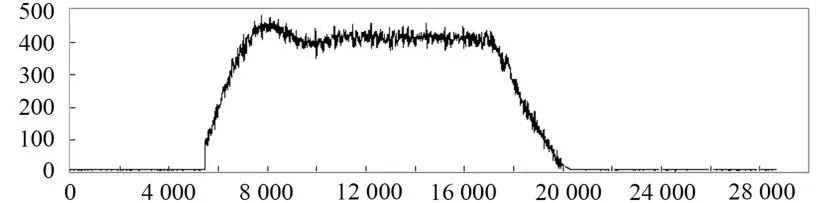
图10 弹鼓运动角速度Fig.10 Angular velocity of projectile and drum motion

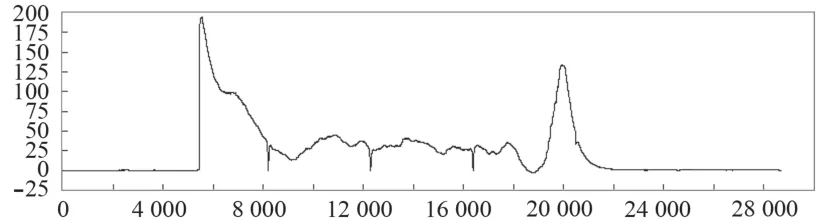
图11 输入扭矩Fig.11 Input torque

试验过程模拟了满载情况下，该型舰炮射击时供弹系统动力学参数，由于仿真计算步数限制，得到的弹鼓运动角速度曲线较短，没有显示出稳定状态，但其基本趋势及最大值等数据与试验数据一致。试验过程中，在停射时输入扭矩会有一个突然增大的波峰，这是由于紧急制动造成的，其变化趋势与仿真计算结果也基本一致。

5 结 语

在射击起始阶段，空载情况下的供弹系统齿轮啮合力波动较大，产生较大的加速度，因此振动较大；满载情况下的齿轮啮合力大，加速过程相对空载时较平稳。通过模拟射击试验，试验数据与仿真计算数据基本一致。根据以上供弹系统动力学分析结果，可以为供弹系统的强度校核、结构优化提供较为可靠的分析依据。