在深度学习中培育推理素养——《分数的基本性质》教学案例与思考

朱荣武（特级教师）

【教学内容】

苏教版五年级下册第66、67页。

【教学片断与思考】

一、推理素养培育，现状如何？

推理，是人们工作和生活必备的素养与能力。但在笔者所见的一线教学中，推理能力培养仍然像“空中花园”，美丽而又虚无缥缈。人们一边承认和赞叹培育推理素养的价值和作用，一边又将其培养任务束之高阁，致使培养目标落空。推理素养的培育不仅要有观念上的认知认同，还要有前瞻性的培育路径架构，更要有务实的教学引领和精准的思维引领。要依据教学内容，建立课时、学期、学年的推理素养培育目标体系，要在教学中通过推理思维的具体分析来设计和组织数学活动，让学生在推理思维的亲历中获得方法、体验与经验，从而切实发展推理素养。

二、深度学习，深在何处？

深，不等于难、不在于多。深应深在对知识原理的理解上，深在对数学思想方法的感知感悟上，深在思维过程的“更清晰、更深入、更全面、更合理”上。分数基本性质的发现过程主要是一个合情推理的过程，既要让学生经历“现象——发现——猜想”的归纳推理思维过程，还要让学生经历“从商不变规律到分数基本性质”的这种由此及彼的类比推理过程。在此过程中，既要让学生体会“发现”的乐趣，还要让学生拥有对“发现”负责的态度和改变或修正“发现”的勇气以及理智。同时，依据对大量类似现象的观察、比较、抽象、概括，进而发现并提出猜想，更是深度思维的行进过程。

三、发现分数基本性质的内在思维线索是什么？

从商不变的规律到小数的性质再到分数的基本性质，这些规律都是“从变中把握不变”的发现思维结果。让学生从熟悉的旧知入手，再一次体会并应用这一思维方法去发现新的规律，思维方法的再现和迁移不仅能将学生带到“最近发展区”，而且能有效激发学生的认知动机，为新的发现活动铺设一条思维路径，让探究发现之路“有法可依”“有杖可拄”。

四、猜想要教吗？

从数学思维的活动过程看，人们依据对现象的思考、质疑，发现有规律存在并尝试用语言来描述，这即是发现问题的过程，对发现的问题进行物化整理得到一个结论性的内容即提出问题，这一结论性的内容就是一个有待验证的数学命题。这样，猜想也就诞生了，猜想的提出是思维创新的结果，具有十分重要的教育价值。儿童天生有猜想的冲动，但在数学学习过程中，猜想动机需要教师激发、猜想过程需要教师引领、猜想方法需要教师教授。诚如波利亚所言：我不相信有十拿九稳的方法，用它可以学会猜测……有效地应用合情推理是一种实际技能，并且像任何其他实际技能一样，要通过模仿和练习来学会它。探索发现分数的基本性质时，教师要尽可能地引领学生经历“原生态的”发现思维过程，鼓励和引导学生展开观察比较、质疑反思、抽象概括等思维活动，感受猜想过程，积累猜想经验，在猜想活动中学会猜想。

基于以上思考，我在教学中进行了如下尝试。

●教学片断一：

问题一：观察这几组式子“6÷2→60÷20 和36÷18→6÷3”，你发现什么变了？是怎样变的？什么没变？

问题二：0.1=（）写出一组等式，看看什么变了？是怎样变的？什么没变？

（学生独立研究后，开始全班交流问题）

生：我发现每组式子中被除数和除数都变了，商都没变。

生：第一组式子中被除数和除数同时乘10，第二组式子中被除数和除数同时除以6。

生：我想到了商不变的规律——被除数和除数同时乘或除以一个相同的数（0 除外），商不变。

师：是啊！商不变的规律就是从大量除法式子的变与不变的研究中归纳发现的。第二个问题呢？

生：0.1=0.10=0.100=0.1000=0.10000……可以写出无数个。

生：这里虽然小数末尾的0的个数逐个增多，但小数的大小是不变的。

生：我想到的是小数的性质——小数的末尾添上0 或去掉0，小数的大小不变。

师：是的。小数的性质也是从大量变与不变的例子中研究发现的。看来，研究数学现象的变化特点，从变中把握不变，是发现规律的重要方法和途径。

【思考：从数学学习论的角度看，小数的性质和商不变的规律都是数学抽象和概括共同作用的结果。学习者从“6÷2=60÷20、0.1=0.10=0.100”等特例入手，基于感性认识，通过分析和舍弃，抽出共同点撇开差异点，得到具体事物的简单本质性的认识，然后把这些简单本质性的认识联系起来，通过归纳逻辑推广到同类事物，从而形成一种普遍性的认识。在这一认知过程中，认知发现的思维起点和线索都是“于变中把握不变”，学生在学习小数的性质和商不变规律的时候已经在不经意间应用到了这一思维方法，对此已经有了较为深刻的体验，积累了相关思维经验。本节课通过两个研究问题再一次唤醒这一思维方法和经验，并让学生在对这两个规律发现过程和方法的比较、归纳中获得“研究数学现象的变化特点，从变中把握不变，是发现规律的重要方法和途径”这一方法性认知，思维方法、经验的再现和重组，优化了学生的认知结构和方法系统，让思维水平再一次得到了切实提升。这些，为本节课的学习奠定了坚实的方法基础。】

●教学片断二：

师：这两个圆前后什么变了？什么没变？

生：这里平均分的份数变了，从3 份变到6 份再变到9 份，圆的大小没变。

生：涂色部分的大小也没变。

师：比较这些分数，你有什么发现？

生：它们是相等的。

师：相等？这怎么可能？它们的分子和分母都不一样啊？

生：虽然它们的分子分母不同，但表示涂色部分的大小是一样的。

生：是的，涂色部分的大小始终是没变的。

生：无数个。

（学生在《学习单》上先研究再交流展示）

生：从左往右看，这里分子分母都乘了2、4，反过来都除以了2、4。结果还是相等的。

师：比较这三组分数的分子分母的变化特点，说一说它们都是怎么变的？

生：分子分母要乘都乘，要除都除。

生：乘的数都一样，除的数也都一样。

生：如果乘或除的数不一样的话，分数的大小就变了。

生：那个数必须是同一个数才行，如果是不同的数，结果就不一样了。

师：也就是说同时乘的数是一个小数，分数的大小也不变。

师：通过刚才的研究，你们能说说自己有什么发现吗？

生：在分数里分子分母变了，但分数仍可以相等。

生：分子分母同时乘一个数，或者同时除以一个数，大小不变。

生：这个数必须是同一个数。生：而且不能是0。

师：为什么不能是0？

生：因为0 不能做除数，也不能做分母。

师：是的。大家能不能把这个发现总结的更简洁一些？

……

【思考：猜想的生成总是源自对特例的观察，人们对特例相似性的归纳总结便初步得出了一个猜想。然后在好奇心的驱使下，人们会不断地寻找相关例证来证实或证否已有猜想，若进一步的例证能够证实已有猜想，则猜想的可信度进一步得到强化，思维进一步清晰，内容进一步明朗。在此基础上通过数学语言予以总结描述，这样就得到了一个明确陈述的一般命题，对命题的进一步例证直至证明，猜想才可以成为真理。这即是归纳推理的一般过程。在儿童的世界里，尤其是在课堂学习的环境下，儿童的思维尚达不到这样的自觉，仍需要教师的引领和引导。本节课，我以归纳推理的思维过程为线索，以切实经历归纳推理的思维过程为目标，带领学生经历了“建立特例——观察——比较——概括——引发联想——初步得出猜想——再次研究特例——强化猜想——归纳总结”等思维过程，不仅发现了数学知识，更积累了“归纳——猜想”的数学活动经验，进一步增强了发现问题、提出问题的能力。】

●教学片断三：

师：同学们真是厉害！从两组相等的分数中得到了一个数学发现，为了稳妥起见，咱们再找一个例子来验证一下吧。

（呈现下图）

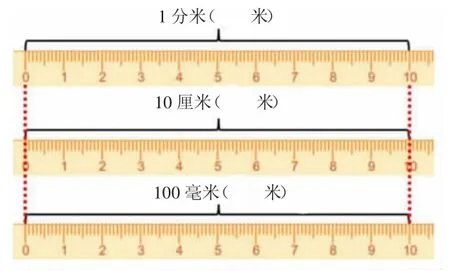
师：从中你发现“变与不变”了吗？

生：我发现它们的长度是不变的，单位变了，数也变了。

生：这三个分数是相等的。

师：这个例子能说明刚才的发现是对的吗？

生：能！分子分母同时乘或除以了10、100。

师：现在你们确信这个发现是对的吗？

生：确信！

师：为什么底气这么足？

生：因为我们刚刚研究过了。

生：因为分数的分子和分母是同时乘或除以一个相同的数，0除外。

生：因为这些分数的分子分母变了，但是涂色部分的大小是不变的，所以始终相等。

师：是的，同学们说的有道理。但是数学家和你们的想法不一样，他们认为虽然在这三组分数中是这样，但是分数有无数个，得保证所有的分数都有这样的特点才行，你们觉得有道理吗？

生：有道理。如果有的分数不是这样，那这个发现就不对了。

师：是啊！那怎么办呢？

生：那就一直研究下去。

生：那不行，这样你一辈子也研究不完的。

生：那怎么办？

师：这时候，就需要想办法“证明”了。今天老师就带领大家做一次“证明”好不好？大家还记得除法的商不变规律吧，分数和除法是有联系的，你能用商不变的规律来解释说明分数的基本性质吗？

（学生展开说理活动）

【思考：一个数学发现（猜想）是否正确，还需要验证，这一点学生是理解并认同的，这说明五年级的学生已经具备了一定的科学态度和理性精神。但这种态度和精神尚有局限性，其一他们认为验证就是继续举例，方法欠缺；其二他们认为只要再找到若干正例即可说明发现是对的，严谨性不足。于是在以1 分米的长度为例验证后，我和学生展开进一步的对话，并以数学家的想法让学生知道：验证，还有很多工作要做。这种“理智上的诚实”品质是需要结合具体的学习活动来培养的。在学生思维受阻之时，及时引出“证明”这一逻辑论证方式，尽管学生尚不理解证明的真正内涵，但至少可以知道：“证明”是一种有效而且必要的方法过程。用商不变规律来解释说明，这本质上是一个类比推理的过程，虽算不上严格意义的证明，却以儿童可接受的方式经历了“证明”过程，并对类比推理的思维过程和方法有了深刻的体验。】