把握整体摆脱定势借助题组形成策略——以两类解决问题的调查和分析为例

吴巧娜

解决问题是小学数学教学的重要内容，其中两步计算解决问题种类繁多。在基本的“加减乘除”四种关系式中，可以组合成“加加、加减、乘除、除加”等16 种复合关系。而每种复合关系，还可以细化成多种类型。张天孝教授为国内从20 世纪50年代末至今的所有通用教材中的应用题做了几千张卡片，进行分析、比较、研究后得出：两步复合应用题从数量关系来看，大致有93 种题型。笔者所在的团队对照这93 种题型，找出了人教版中所有的两步计算应用题，进行了初步的整理，形成了一份93 题的样卷。对8 个学校（城区、乡镇各4 个）共641 名四年级学生进行了第一次测试调查，结果统计后发现：错误主要集中在“比多比少”“倍数问题”这两类问题当中。

这两类解决问题的起始教学都在第一学段，那么第一学段的学生解决这些问题又会是怎样的情况？第二次调查测试由此展开：这次调查对象是三年级共158 名学生，从中挑选了两类问题当中典型的20 道错题，统计后发现：三年级的得分率竟然反超了四年级。本文试着对这两类解决问题的检测情况进行分析，结合教材编排、教学方式寻找错因，以期获得相应的解决策略。

比多比少典型错题展示错题 得分率 错误展示 错因分析四年级 三年级一班和二班共有78 个学生，一班40 个学生，二班比三班少4 个学生，三班有多少个学生？75.9% 80.5%78-40=38 个38-4=34 个梨有34 个，苹果18个，橙子31 个，橙子比梨和苹果个数的差多多少个？24.7% 56.2%34+8=52（个）52-31=21（个）少、和、差等关键词产生了强烈的思维定势。学生对关键词孤立地理解，而没有去深究它们之间的数量关系。

71.7% 70.3%倍数问题商店运来一批红糖，卖出20 千克，卖出的是剩下的4 倍。这批红糖一共有多少千克？20×4=80 千克80+20=100 千克参加合唱队的人数是舞蹈队的3 倍，参加合唱队有75 人，参加器乐队的人数比舞蹈队少8 人。参加器乐队的有多少人？55.6% 67.5%3×75=225 人225-8=217 人把“一倍数”当成“几倍数”，而当题中的信息表述顺序颠倒时，这个错误就更明显了。

【教学过程】

一、教材梳理

对于这两类解决问题，人教版教材的教学布局如何？第一学段的教学对于第二学段的学习又会有怎样的影响？仔细翻阅教材，发现人教版中关于两步计算解决问题集中编排在三年级，统计了这5 册的教材编排分布与题量设置情况：

三年级上册19 题，以“乘除”和“除乘”为主，解决的是归一、归总问题。

三年级下册31 题，以“乘乘”和“除除”为主，解决的是连乘和连除问题。

四年级上册7 题，编排零散，题量较少。

比多比少 倍数问题内容 相差数 求比一个数多几或少几 倍的认识册数 一年级下册 二年级上册 三年级上册题量（包括例题、练习和总复习） 9 题 10 题 8 题没有编排 A 与B相差几个？A 有15 个，A 比B 少4 个或A 比B 多4 个，求B 有多少？求一倍数的问题

通过对教材编排情况的梳理，笔者发现：教材编排较散、题量不足、题型欠缺、问题过于单一、缺乏逆向思维的引导、关键词引起的思维定势，都是导致学生解决问题能力不足的主要原因，三、四年级成绩反超也有迹可循。

二、原因诊断

1.教学中的关键词机械强化，缺乏联想。

在学习解决问题的初期，教材其实一直都在给学生进行关键词的强化，譬如在学习用加法解决问题时，一般都有“加、和、一共、……比……多”等明确指向加法策略的关键词。同样在学习减法解决问题时，也有“吃掉、还剩、卖出、……比……少”等明确指向减法策略的关键词，特别是“多和少”，学生的脑海中这两个关键字应该是最根深蒂固的了。而低段教材中解决问题解答方式都与关键词的字面指向意思相同，这就使学生不断地在进行强化，逐渐把关键词“多、少”优化为解决问题的首选策略，成为一种思维定势，而忽略数量之间的关系分析与思考，对问题解决往往表现出一种机械的策略重复。

要想让学生从一个关键词马上联想到一个数量关系，脑海中有这类问题的清晰表象，譬如：“少——相差数——大数-小数=相差数——（）比（）多或少”，这种从一个字到一组关系的思维，是需要不断的积累的。而教材的题量不足、题型欠缺，如果我们按部就班根据教材进行教学，那么学生的这种思维反应是无法建立的。

2.教学中的问题过于单一，缺乏整体。

人教版现在对解决问题已经没有专门的单元编排，而是以基本的数学思想方法为主线来选择和安排教学内容，往往以计算伴随着应用相融合的形式编排，穿插在不同的单元之中。而且题型比较单一，只有基本题型，缺少变式练习和逆向练习。解决问题的整体性不强，这在一定程度上削弱了学生对“问题”的敏感性和数量关系的分析能力。

对于解决问题的呈现，教材中不可能对每种题型都面面俱到，但是必要的题型还是需要涉及的，如：倍的认识中求一倍数的题型。因为只有整体呈现，才能帮助学生在学习中建立完整的问题模型。

三、对症下药，形成策略

◆策略一：落实整体思想，摆脱思维定势。

怎样做才能既揭示出问题自身的规律，又不至于使它成为一种思维定势呢？

给关键词建立关联、开展关系训练。引导学生转换思考角度，从整体上把握，全面观察数量之间的关系，找到问题的关键所在，可以回归到计算教学的原点，从两数之间关系结构的表征着手。

譬如：一年级下册有一类求“原来”的解决问题，是学习难点。我们可以把原来、新买、现在这三个关键词通过数的组成和分解建立关联，有了这样一个联系，学生就能更清楚地分析这类解决问题的结构。对解决问题的特点进行提炼和概括，学生的关注点不再锁定于表示加减暗示的关键字，而是回到数量之间的关系分析与思考，关注量与量之间的联系，从而避免因关键词误用而带来的解题错误。同时利用适当的题组训练，对这三个关系进行一定的训练，建立通过事情发展顺序的分析，明确“原来”与总数和部分数的关联，从而避免仅仅依靠对关键词的判断盲目选择算法，继而提高学生根据问题结构来选择算法的能力。

◆策略二：借助题组训练，加强逆向思维。

从心理学的角度来说，学生都习惯于顺向思考，遇到逆向思考的问题，思维就容易受阻。对于一些运用逆思维解答的数学问题，需要通过适当的题组训练，加强学生的逆向思维，提高学生根据问题结构来选择算法的能力。

以倍数问题为例，可以通过图文对比、图文转换的题组练习，逐步建立求一倍数的模型。同时注重借助线段图表征数量关系，再通过一个数量的修改，又变化出另一组题。这样两组题型对比分析，极力让学生找准一倍数，直观地将线段图与数量关系进行架构，逐渐建立关于“倍”的完整的问题模型。

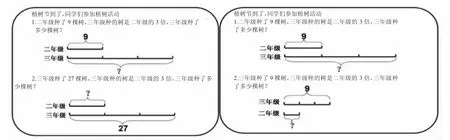
任何一个顺向问题都可以变为逆向问题，通过可逆性的变化，问题可以变成条件，条件又可以转化为问题，这样可以得到一组习题。在题组的解答过程中，积累从关键词到一组关系的思维反应，才能更好地构建两步计算解决问题的完整模型。

解决问题虽然已经不再自成体系，而是以基本的数学思想方法为主线来选择和安排教学内容，往往以计算伴随着应用相融合的形式编排，更加关注问题的发现与提出、学生解决问题策略的多样化和综合能力的发展。所以，作为一线教师的我们，只有透过教材，审视教材，注重对每一个独立问题的分析和策略的提炼，引导学生将看似独立的若干问题构建成一类问题原型。这样学生在解决问题时就不会表现出机械的策略重复，而是能跨越表象看本质，通过多元表征得到多样的解题策略，并将多种解题策略归于同一类问题解决策略的结构中，形成完整的问题结构，达到解决一些问题到解决一类问题的目的，提高学生思维的变通性，让学生在解决问题这条路上走得更顺、更远。