聚焦概念本质促进数学理解——《比的认识》教学设计与评析

韩淑萍 邵 虹

比是一个重要的数学概念，而学生理解比的意义往往比较困难。教材呈现了丰富的生活情境，通过解决“长方形的长与宽之间有什么关系？”的数学问题，揭示可以用长与宽这两个数的比刻画长方形的形状特征，由此引出同类量的比。教材又通过飞船运行路程与时间的比较，引出非同类量的比，从而抽象出比的意义：两个数的比表示两个数相除。掌握比的概念和意义，为以后进一步学习圆周率、百分数、统计以及比例奠定基础。此外，比和分数、除法有密切的联系，两个整数相除（除数不等于0）可以用分数表示它们的商，也可以用两个数的比表示，两个数的比又可以用分数的形式呈现。因此，借助比的认识，发展学生对分数和除法的认识，沟通知识之间的内在联系，能从量与量的关系角度认识比，提高学生灵活运用知识解决问题的能力。

【教学过程】

一、创设情境，体会学习“比”的必要性

1.博物馆要选五名志愿者当解说员，根据组委会的要求，每一位志愿者需要交五张大小不同的照片。淘气同学上交了五张照片，结果有两张照片被退回，导致他没能实现当志愿者的愿望，究竟是什么原因呢？（课件出示五张照片）

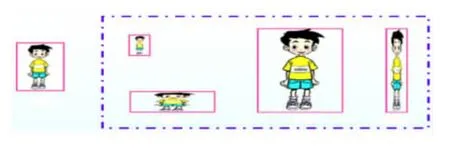
师：哪几张照片被退回？又是哪几张照片与A比较像？

生：照片C 太扁了，照片E 变窄了，照片B、D和A 比较像。

师：这仅仅是我们观察得出来的结论，有时并不能说明问题的本质，同学们能用数学的知识来解释照片B、D 和A 比较像的秘密吗？

生：需要这些照片的长、宽的数据。

师：得到这些长方形的长和宽，有什么意义呢？

生：我们可以求它们之间的倍数关系。

师：看来，这些照片像不像，与每张照片的长、宽之间的“关系”有密切的联系。这种研究的方法非常有价值！

2.把这五张照片搬到方格纸上来研究（每个小方格的边长为1 厘米），出示方格图：

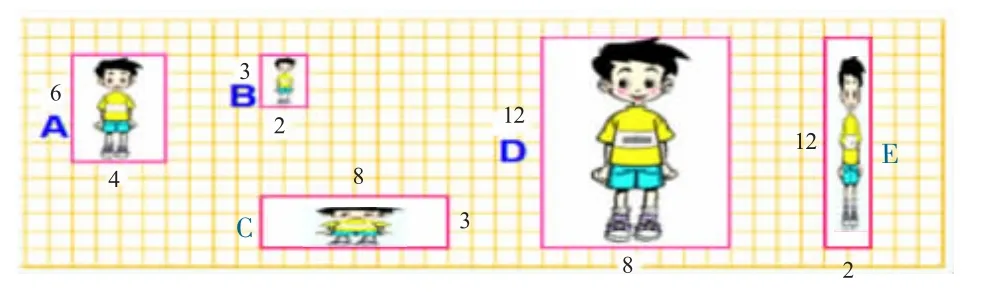
师：这些照片都是长方形，它们的长和宽之间有什么关系？边观察、边测量，并将研究结果填写在表格中。（学生同桌两人为一组，对照片A、B、C、D、E的长与宽分别进行测量与计算，填写表格并汇报）

照片（长方形） 长 宽 长是宽的几倍 宽是长的几分之几A 6 4 6÷4=1.5 4÷6=2 3 B 3 2 3÷2=1.5 2÷3=2 3 C 8 3 8÷3≈2.7 3÷8=3 8 D 12 8 12÷8=1.5 8÷12=2 3 E 12 2 12÷2=6 2÷12=1 6

师：现在请大家仔细观察表格中的数据，你发现了什么？

生：照片A、B、D 中，虽然长和宽的长度各不相同，但是长除以宽都是1.5 倍。反过来，宽都是长的

生：我知道照片C、E 和照片A 不像的原因了。它们的长除以宽得到的倍数都不一样，没有按比例放大或者缩小。

师：同学们说得非常棒！A、B、D 三张照片之所以像是因为各自的长都是宽的1.5 倍，宽都是长的看来照片像不像与它们长宽之间的倍数关系有关。

【评析：比的概念比较抽象，如何让学生理解概念并认同概念产生的价值呢？教师首先创设“淘气同学落选原因探究”的生活情境，通过比较照片像不像的活动，引导学生把对比的关注点落到对长方形长和宽两个量上。当学生模糊地感觉到需要知道照片的长、宽数据时，教师又因势利导借助方格纸测量并探究长与宽之间的倍数关系。在对两个量关系描述的基础上，认可比的价值，认识到学习比的必要性。教师设计的表格，不仅呈现了像与不像两类照片的长、宽关系，还从“长是宽的几倍”“宽是长的几分之几”两个维度进行关系比较，为后面探究比与除法、分数的关系奠定基础。】

二、聚焦本质，理解比的意义

1.理解同类量的比。

师：“长是宽的几倍？宽是长的几分之几？”都是用来表示两个量之间的倍数关系，有时我们也把两个数量之间的关系说成：长和宽的比是6∶4，宽与长的比是4∶6。其实在人体上存在很多这样的倍数关系：

（1）成年人的头长与身长的比约是1∶7。

（2）两手平伸的长度和自己身高的比约是1∶1。

（3）握紧拳头，绕拳头一周的长和自己脚长的比约是1:1。

（4）人的心脏大小与拳头大小的比约是1∶1。

（5）成年人腿长与头长的比约是4∶1。

（6）成年男子的肩宽与头长的比约是2∶1。

【评析：比表示的是两个数之间的关系，而数量之间的关系有很多，比表示的是怎样一种关系呢？教师这样的设计尊重了比这一概念的形成和发展。比的概念是由比较两个同类量之间的倍数关系而产生，而后再推广到两个不同类量的比。因此，初学比的概念时，借助于生活常识和已有知识基础，从固定的倍数关系引出，体现了比的发展过程，为学生理解比的意义提供了强有力的支持。】

2.理解非同类量的比。

马拉松比赛，李明跑40 千米用了2 小时，陈浩用3 小时跑了45 千米。

师：能用比来说一说它们之间的关系吗？生：李明和陈浩跑的路程比是40∶45。

生：李明和陈浩跑的时间比是2∶3。

师：谁跑得更快呢？

生：可以用路程除以时间，比较他们的速度。

生：李明的速度为40÷2=20（千米/时），陈浩的速度为45÷3=15（千米/时），所以李明速度更快一些。

师：除了可以用“路程÷时间”来表示速度，我们也可以用比来表示路程和时间的关系：李明路程和时间的比是40∶2，陈浩路程和时间的比是45∶3。

【评析：比既可以表示同类量的关系，也可以表示非同类量之间的关系。如何沟通两者间的内在联系，将知识的发生、发展梳理成连贯的脉络呢？教师巧妙地设计了一个行程问题，分别呈现路程、时间、比谁更快等信息和问题，将同类量的比拓展成非同类量的比。让学生意识到用比不仅可以表示李明和陈浩的路程比和时间比，还可以表示出路程与时间的比。由此，学生对比的意义理解更深刻与全面。】

3.认识比及各部分的名称。

师：什么叫做比？请自学课本48、49 页有关比的知识。

（1）出示自学提纲。

①什么叫做比？②比的读法和写法。③比各部分的名称叫什么？④怎样求比值？

（学生汇报比的意义，教师板书：两个数相除又叫做两个数的比。分析关键词：相除、比）

师：能举一个例子吗？

生：6÷4 就可以写成6∶4。

（2）选择几个表格中的除法算式，改写成比的形式，并说一说前项、后项和比值。

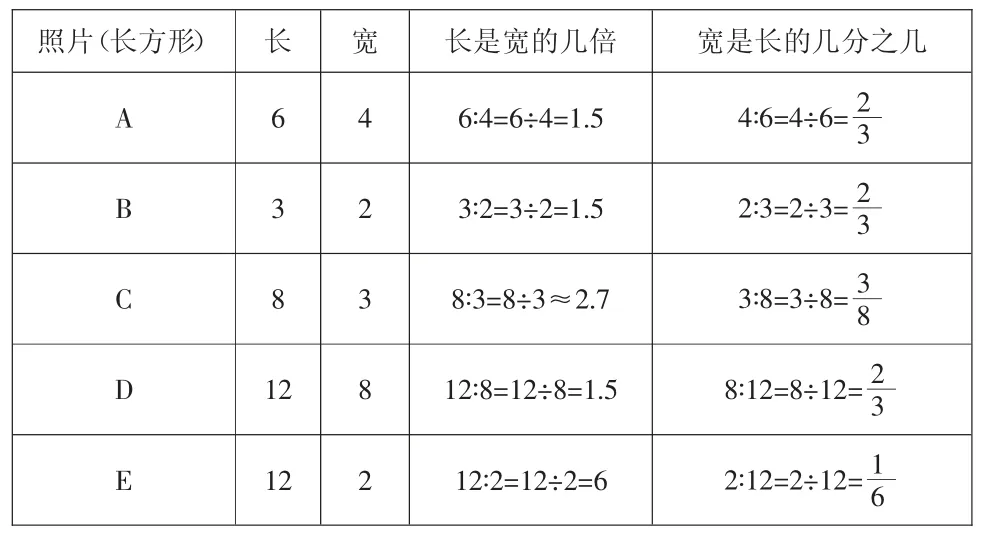
照片（长方形） 长 宽 长是宽的几倍 宽是长的几分之几A 6 4 6∶4=6÷4=1.5 4∶6=4÷6=2 3 B 3 2 3∶2=3÷2=1.5 2∶3=2÷3=2 3 C 8 3 8∶3=8÷3≈2.7 3∶8=3÷8=3 8 D 12 8 12∶8=12÷8=1.5 8∶12=8÷12=2 3 E 12 2 12∶2=12÷2=6 2∶12=2÷12=1 6

比值通常用分数表示，也可以用小数或整数表示。

师：6∶4=1.5，3∶2=1.5，12∶8=1.5，看来比还有这样的特点，前项和后项可以不断发生变化，但是倍数关系不变，这就是照片A、B、D 相似的原因了吧。

（3）小知识：“∶”号的由来。

师：比号的来源有一个故事，大家来了解一下。

莱布尼茨是数学史上最伟大的符号学者之一，堪称符号大师。他认为，因为两个数相除又叫做这两个数的比，所以比号和除号有一种亲缘关系。而比号与除号又不能共用，所以把“÷”中的小横线去掉，于是“∶”就成了比号。

【评析：在教学了可以用比来表示两个同类量和非同类量的基础上，直接抽象出比的意义：两个数的比表示两个数相除。这一意义是认识比各部分的名称、求比值的直接保证。对于正确认、读、写比和认识各部分名称的内容，教师采用了自学课本的方式，在引导学生改写表格中的除法算式时，渗透了比与分数和除法之间的内在联系。】

三、探索发现，比与除法、分数之间的关系。

1.比、除法、分数之间的联系。

师：通过学习，我们了解了比和除法有一种亲缘关系，比也可以写成分数的形式，那它们究竟有怎样的联系呢？同桌互相交流。

生：比的前项相当于除法中的被除数，比号相当于除号，比的后项相当于除数，比值相当于商。

生：比的前项相当于分子，比号相当于分数线，比的后项相当于分母，比值相当于分数值。

2.比、除法、分数之间的区别。

师：既然比与除法、比与分数有这么多的“相当于”，那为什么有了除法还需要学习比呢？比和除法有什么区别？为什么有了分数还需要学习比呢？比和分数又有什么区别？

师生共同交流、讨论后得出：除法侧重于一种运算，分数强调结果。比相比除法更侧重两个量之间的关系；比相比分数既可以用前项、后项的形式又可以用分数的形式，更灵活多变一些。

根据交流结果，整理成一张表格呈现。

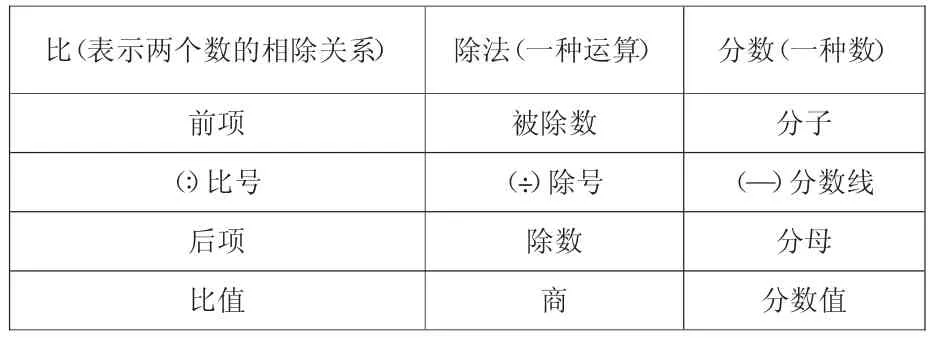
比（表示两个数的相除关系） 除法（一种运算） 分数（一种数）前项 被除数 分子（∶）比号 （÷）除号 （ ）分数线后项 除数 分母比值 商 分数值

【评析：比、除法与分数三者之间的关系，学生应该认识到什么程度？如果是外在的“相当于”联系，我们认为即使教师不刻意教学，学生也会达成。因此，追问三者的区别就是本环节的核心所在。这个环节的设计，教师聚焦概念的本质，从意义上让学生区别体会：分数、除法和比都可以表示相除的关系，但是分数强调结果，除法侧重运算，而比既可以用“几比几”的形式表示两个量之间的关系，还可以根据需要用比值表示比较的结果。在本设计中，教师将三者之间的关系渗透在教学的各个环节。如，引入部分用三种形式比较照片长、宽的倍数关系，认识比、各部分名称及求比值的教学中让学生自然感悟到比能简洁、直观地反映两个量的倍数关系。】

四、拓展辨析，促进知识理解

1.有A、B、C 三个质量完全相同的苹果摊位，哪个摊位的便宜呢？用今天学习的比的知识来解答。

2.辨析比赛中的“比”。

出示“两队比分2∶0”的课件，使学生了解体育比赛中的比。

师：比分2∶0 中的“2”表示什么？“0”表示什么？

师：比赛中的“比”和今天学习的“比”一样吗？它能表示两个量之间的倍数关系吗？

引发学生争论，破解生活中的比与数学中的比的本质区别。

3.欣赏“黄金比”。

师：你听说过“黄金比”吗？

当一个物体的两个部分，较大部分与整体之比等于较小部分与较大部分之比0.618∶1 或1∶1.618，比值等于0.618 时就成为“黄金比”。“黄金比”给人一种优美的视觉感受，所以，许多建筑作品、艺术作品都是按“黄金比”来设计的。

【评析：数学知识与现实生活密切联系，鲜活的情境往往是数学学习的好素材。教师在“拓展辨析”环节，首先创设了“哪个摊位的苹果便宜？”的现实情境，引导学生解决非同类量比的问题，体会比更能直观、便捷地表示两个量之间的关系。此外，六年级的学生生活中接触到、最熟悉的莫过于比赛中的比分。但是比分只是一种记录比赛双方得分的方式，是比较大小的，是相差关系，不是相除关系。通过真实情境问题的辨析，进一步加深对数学中比的认识，这种去伪存真的过程，对聚焦概念本质、促进意义理解具有十分重要的价值。而黄金比的巧妙介入，不仅使课堂生出很多趣味，而且表达了人们创造美的智慧。】

五、回顾整理，完善知识结构

1.今天我们学习了哪些知识？

2.我们是怎样学习的？

3.你还有哪些新问题？

4.完成课后的练习。

（1）练习本上完成教材第49 页的“做一做”第1、2 题和52 页的第3 题。

（2）查资料了解“生活中的黄金比”。

【评析：教师在课的尾声为学生提供了回顾知识获得、整理所学知识的机会，帮助学生形成良好的学习方法和良好的学习习惯。同时，在回顾整理的过程中，让学生把知识串联在一起，构建完整的知识体系，实现对知识理解由点到面的突破。】