LDPC编译码算法的仿真分析∗
2019-06-01詹平红李红星尹爱兵
詹平红 李红星 尹爱兵
(1.陆军炮兵防空兵学院 合肥 230000)(2.安徽新华学院 合肥 230000)
1 引言
通信目的在于传输信息,通信系统的作用将信息由信源传送到信宿。在信息传输的过程中,不可避免会受到信道中的噪声的干扰,从而导致了可靠性的降低。所以,如何提高系统的可靠性,在设计系统时可以合理的选择调制制度,解调方式以及发送功率等,在仍不能满足要求时,可以考虑差错控制了,信道编码的作用就是进行差错控制。信道编码的实现原理就是对传输的信息码元按一定的规则加入监督码元,组成抗干扰编码。从而提高系统的可靠性。
LDPC码是一类可以提高系统可靠性的信道编码技术,是一种低密度的线性分组纠错码,可以用非常稀疏的校验矩阵H或二分图来描述,在基于置信传播的迭代译码条件下具有逼近Shannon极限的性能[1~2]。根据校验矩阵H行列中1的数目是否相同,可以将LDPC码分为正则LDPC码和非正则LDPC码。本文主要研究的是正则LDPC码。
Gallager最早给出了正则LDPC码的定义,具体来讲正则LDPC码的校验矩阵H满足下列三个条件:
1)H矩阵的每行“1”的个数是相等;
2)H矩阵的每列“1”的个数是相等;
3)与码长和H矩阵的行数相比,和都很小。
LDPC码往往具有较大规模的校验矩阵,校验矩阵的构造不同,LDPC码的性能和编译码的复杂度也不相同。研究者提出了各种降低复杂度的编译码算法[7],使得LDPC码在通信领域的使用成为可能。
2 LDPC编码算法
LDPC编码是以校验矩阵H为前提,再由校验矩阵获得生成矩阵,生成矩阵再产生不同的码字[3~4]。因此,设计校验矩阵H也是LDPC码编码的关键。
LDPC码校验矩阵H的一般构造步骤如下:首先生成一个的全0矩阵,然后随机地将每列中的j个0置换成1,每行当中的k个0置换成1。但是置0还置1的过程中,有两种情况是必须要避免的:一种情况是在H矩阵构造时要避免4环以及短环的存在。小循环会对系统性能带来不良的影响,导致消息在两组点之间的反复传递,难以得到更新,与迭代译码的思想初衷相违背,是必须清除的一种结构。另一种情况就是比特节点所连接的校验方程过于集中,如果这些特节点都出错时,校验方程都不能检测出错误的存在。对于计算机仿真最简单最实用的是代数构造法[5]。
假设要生成一个无4环的规则(n,j,k)LDPC码的校验矩阵Hm×n。当j<m时,其中j为列重,m为校验节点的个数:
采用以下步骤获得H矩阵:
1)选取 k个素数 p1,p2,…,pk且 p1>p2>…>pk>2;(pi,m)=1,i=1,2,……k;2p1+2p2+2p3<m
2)把m个校验节点编号为0,1,…,(m-1),依次均匀地放在一个圆上。
3)随机选取一个校验节点i,以pi为步长顺时针移动(m-1)次,连同节点i共计依次走过m各点,记为posi。把跑遍的点依次排列组成一个序列pos,完成了一轮操作。
4)依次取素数pa,a=2,3,…,k,重复第三步。
5)将pos中的mxk个元素按每j个一组进行划分,每组对应一个变量节点 xi与 eji,eji+1,…,eji+j-1相连,完成了无4环规则LDPC码的H构造。
代数构造法中k个参数的选取方法,先获取一张适当大小的素数表,并将表中的素数从小到大排列,从素数表中划去大于m/2的素数,并将与m不互素的数从表中划去,然后选定两个较小的素数q1,q2,计 算l1=2q2+q1,l2=2q2-q1,l3=2q1+q2,l3=2q1-q2如果li为素数,将其从素数表中划去,从素数表中选定下一个较小的素数,作为q3,然后从已选定的素数中再选取一个作为q,令q2=q3,q1=q,再计算一次li,如果为表中的素数,又将其从表中划去,重复这一过程,直到选定k个素数为止。
以规则(486,3,9)LDPC码为例,首先用上述方法选取9个素数,再有代数构造法确定校验矩阵H,利用spy(H)画出矩阵H中非零元素的分布情况。
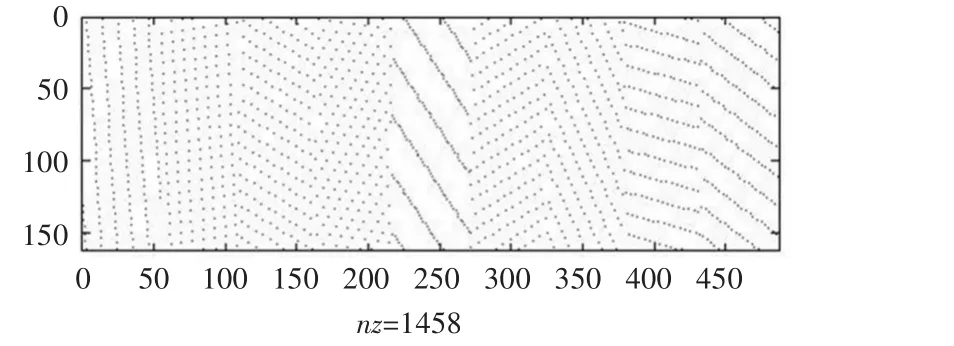
图1 矩阵H中非零元素的空间分布
通过高斯消元法使校验矩阵H消元[6],获得具有近似下三角矩阵的特殊形式如图2所示。
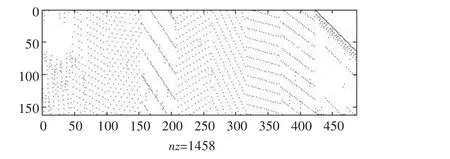
图2 近似下三角矩阵H
3 LDPC译码算法
LDPC码有硬判决和软判决的两种译码方式,前者的计算相对简单,译码更快,对硬件设备要求也较小,但是译码性能较差;后者利用了更多接收到的信息,计算相对复杂,译码更慢,对设备要求较高,但译码性能更好。
这里采用的是软判决译码方式,最常用的软判决译码算法是和积译码算法,又称置信传播(Belief Propagation,BP)算法[7~14]。BP算法是充分利用接收到的信道信息,将信道信息转化成可能是0和1的概率信息,这些概率信息在节点之间不断传递,由迭代算法计算概率信息,将节点信息进行更新,这样就可以在接收端判决信号。通过多次迭代计算使得译码结果更加精准,误码率更低。
BP算法具体过程包括先验概率初始化,检验节点想变量节点发送校验消息,变量节点向校验节点发送变量消息,计算似然值进行译码判决,最后,利用校验矩阵H,与译码所得码字x,判断是否满足
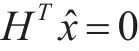
如满足,则译码成功,否则进行下一轮的信息更新计算。直到达到最大迭代次数,则结束迭代。
4 仿真与实现
Matlab是一种用于算法开发、数据可视化、数据分析以及数值计算的高级计算语言的应用软件,是实现通信算法仿真的一个良好平台。但LDPC码的编译码涉及到大量的上快速地实现LDPC编译码算法,是软件部分的关键。根据LDPC编译码的基本原理,需要大量的循环及迭代运算,直接用Matlab的M语言实现仿真速度较慢,如何有效地利用Matlab平台实现编译码算法,软件编码部分在H矩阵构造时采用了上述的代数迭代法,译码部分采用BP算法,并在通信过程中随机加入每帧的错误,译码之后的得到错误bit数,LDPC码的可靠性用误比特率(BER)来衡量[15~16]。
程序中仿真参数设置,LDPC码长为486,列重为3,行重9,信噪比为10dB的情况下进行了仿真实验。仿真程序包括编码程序和译码程序。编码主程序又包括构造H矩阵、信道编码程序及主程序;译码程序包括载波同步、信道译码及主程序。译码是验证LDPC编码的关键,译码主程序实现的功能是载入载波同步模块输出的数据及译码时需要的预处理数据。部分译码程序如下所示。
xxw=324; %源信息数据矩阵
m=162; %H矩阵列数
n=486; %H矩阵行数
Es=2;
r=2/3;
M=1;
Eb=Es/(r*M);%Eb代表平均到每个比特上的信号能量
liezhong=3; %列重
hangzhong=9; %行重
snr=10; %信噪比
sigma=sqrt(Eb/(3*10^(snr/10)));
ber1=0;
ber2=0;
t=1;
while t<61
hanglieH=size(H);
hangH=hanglieH(1);
lieH=hanglieH(2);
ncol=zeros(liezhong,lieH);
nrow=zeros(hangH,hangzhong);
lie1wei=find(H);
for a=1:lieH
for b=1:liezhong
ncol(b,a)=(lie1wei((a-1)*liezhong+b)-(a-1)*
hangH);
end
end
hang1wei=find(H');
for a=1:hangH
for b=1:hangzhong
nrow(a,b)=(hang1wei((a-1)*hangzhong+b)-(a-1)*lieH);
end
end
xyuan=outx1(2,:);
quweishu=5;
demodz(1,:)=ryuan(2,(quweishu+1):(quweishu+756));
for k=1:t
demodz(1,k)=-demodz(1,k);
end
decode; %调用解码程序
for i=1:756
if demodz(1,i)>0 %将接收到的数据进行判
断
demodz(1,i)=0; %如果数据大于0判断为0
else demodz(1,i)=1; %如果数据小于0判断
为1
end
end
decode_out=decoded(1,1:504);
save decode_out decode_out
noe10=sum(abs(demodz-xyuan)); %译码前误码个
数
noe20=sum(abs(decode_out-s)); %译码后误码个
数
nod10=length(xyuan); %编码后码元个数
nod20=length(s); %编码前码元个数ber10=noe10/nod10;
ber20=noe20/nod20;
fprintf('%d %d %f %f %e %e ',t,k,noe10,noe20,ber10,ber20);
t=k+1;
ber1(t-1)=ber10;
ber2(t-1)=ber20;
end
z=1:60;
figure;
semilogy(10。^z);
semilogy(ber1,'-rd');
hold on;
semilogy(ber2,'-bv');
title('LDPC码译码性能曲线');
ylabel('BER');
xlabel('Random Errors');
legend('未经信道译码的误码率','经信道译码后的误码率');
运行结果如图3所示。
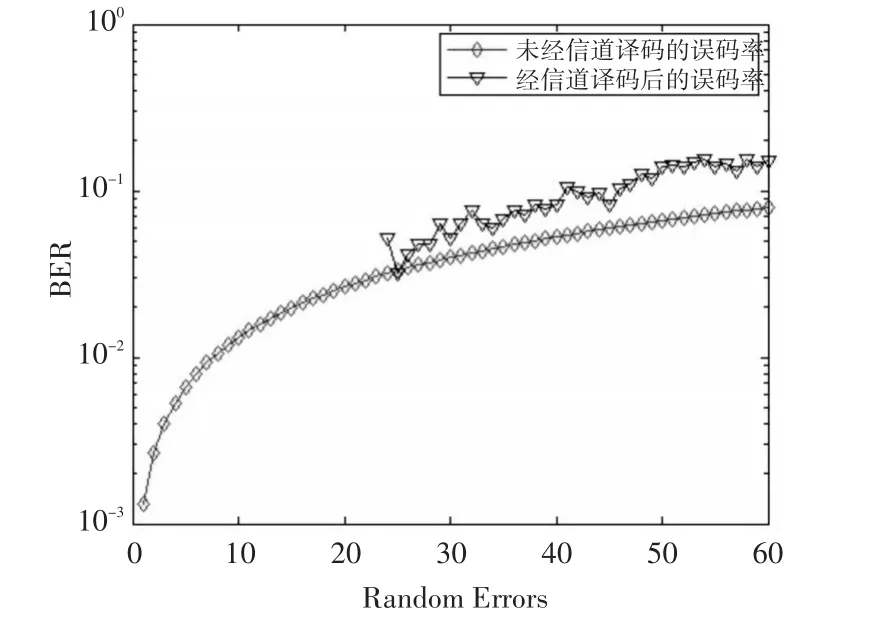
图3 LDPC误码性能仿真分析
仿真程序运行结果可知,编码前的数据矩阵s,其长度为324bit,编码效率达到m/n=2/3,编码效率是比较高,从上图的误码性能分析可以看出规则的LDPC(486,3,9)码编译码性能也是比较优越的,当每帧含随机错误小于等于25bit时可以完全纠错;只有当每帧含随机错误较大,在45bit时才会出现越译码错误越多的现象。
5 结语
LDPC码是迄今为止发现的最接近香农限的信道编码之一,作为一种优秀的信道编码,在现代通信和数据传输系统中将拥有广阔的应用前景。本文主要研究利用Matlab仿真平台实现LDPC编译码的算法,其中包括校验矩阵的构造、编译码的实现,并在噪声干扰下对其误码性能的进行了仿真,验证了LDPC码在编译算法上获得的优越性能。
