基于最优参数选择的EEMD方法的暂态电能质量扰动识别分类∗

赵乾坤 曹玲芝

（郑州轻工业学院 郑州 450002）

1 引言

近些年来，由于各种电力电子器件，非线性负载的使用，电能质量问题日渐严重。电能质量事件对敏感设备及负载造成了极大影响，导致其更易发生故障和误操作。此外，消费者对高质量的电力服务的需求也不断增加，因此电力企业必须改进它们的服务质量，从而获得高质量的电能。

为了提高电能质量，首要任务就是对各种的电能质量问题进行识别和分类。目前对稳态电能质量的研究已经很成熟了，但对暂态电能质量的研究还比较有限，暂态电能质量持续时间短，检测难度大，如何对暂态电能质量指标进行识别和分类具有重要的意义。暂态扰动分为幅值变动和电磁暂态两类，幅值变动主要包括电压暂降、电压暂升、短时中断三种，电磁暂态主要包括暂态振荡和暂态脉冲［1］。通常，这些扰动的识别过程包括两个主要的步骤，特征提取和分类算法。

目前对扰动信号进行特征提取的方法主要有短时傅里叶变换，小波变换，S变换，EEMD等时频域处理方法。短时傅里叶变换［2～3］并不适用于处理暂态电能质量事件。小波变换［4～6］和S变换［7～10］常常被用于处理电能质量事件，这两种方法能同时保证时间和频率分辨率。通过可变的分析窗口长度，在信号的高频部分获取更精确的时间分辨率，同时在信号的低频部分获取更高的频率分辨率。但对于不同的电能质量事件，小波变换的性能依赖于母小波选择；S变换的分解效果则受制于高斯窗的性质，其次 S变换的计算量太大。EEMD分解［11～13］是一种基于信号的自适应分解，不需要预先设定基函数，同时兼有小波分析的优点，但其辅助添加的噪声幅值大小及添加次数影响该算法的性能，对于电能质量事件，对于如何准确选择辅助噪声的幅值和添加次数还没有论文提出。

常用的分类算法有神经网络，决策树，支持向量机等方法。神经网络［14～15］具有结构简单，能较好地处理噪声数据的优点，但是其经常在局部最小值上收敛，而且如果训练时间持续太久，往往会过度拟合。支持向量机［16］在解决小样本、非线性及高维模式识别中表现出许多特有的优势，能收敛到全局最小值，然而它依然存在内核参数选择问题，选择不当容易过度拟合。决策树［17～18］结构简单，不需要训练，计算量小，但其抗干扰能力太差。本文采用模糊C均值（fuzzy C-mean，FCM）算法作为分类器用于对暂态电能质量扰动进行识别分类。FCM算法易实现、速度快且抗噪能力强。

针对电能质量事件，合理地设置EEMD方法的辅助噪声幅值及添加次数两个重要的参数，进一步改善了模态混叠问题，提取信号有用的特征向量作为分类器的输入，实现对扰动类型的分类。

2 基于最优参数选择的EEMD方法

2.1 EEMD原理

EEMD［19］方法由EMD方法发展而来，它属于噪声辅助分析算法，比EMD的尺度分离能力更好，EEMD方法的过程如下所述:

1）将一个预定义噪声幅值的白噪声添加到原始信号进行分析。

2）使用EMD方法分解新生成的信号。

3）添加不同的白噪声，重复上述信号分解，添加的白噪声的振幅是固定的。

4）计算整体分解结果作为最终结果的手段。

使用这个信号处理方法，多成分信号x（k）能被分解为有限个固有模态函数（IMF）和一个残留分量，如式（1）所示:

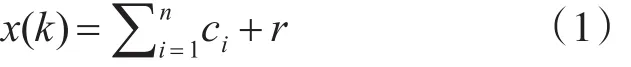
其中，n是IMF的数量，ci是第i个IMF分量，r代表残余分量。

2.2 最优参数选择

对于不同的待处理信号，EEMD方法的两个关键的参数，辅助添加噪声的幅值AN和添加次数NE的选择不是固定的。针对电能质量信号，选择最佳的辅助添加噪声幅值，有助于改善EEMD方法的性能，提高尺度分离性能，减少模态混叠。当噪声幅值确定好后，增加迭代次数，有助于减少各IMF分量中残留的噪声。

假设待处理的电能质量信号为xo（k），由主要信号成分，背景噪声和一些低相关信号分量组成。应用EEMD方法处理电能质量信号，该信号被分解为多个IMF分量。选取与原始信号相关性最高的IMF分量，称之为cmax（k），其包含了原始信号的主要信号成分。对于添加不同噪声幅值的信号，评价EEMD的分解性能的优劣关键在于其主要信号成分是否与噪声、其他低相关的信号成分分开。本文引入了均方根误差（RMSE）指标，用以评价不同噪声水平下的EEMD方法的性能，其表达式如式（2）所示。

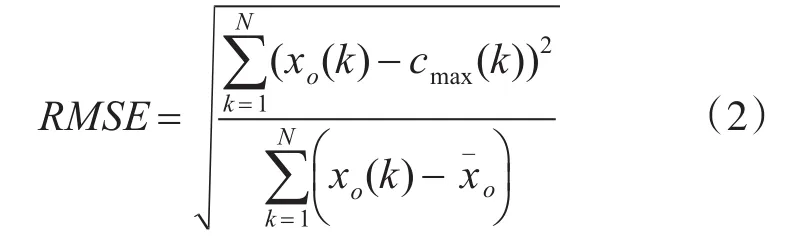
xo是原始信号的均值。

RMSE越小，说明所选的cmax（k）越接近原始信号xo（k），也就是说cmax（k）不仅包含了包含了原始信号的主要成分，还包含了部分噪声和其他低相关分量，因此cmax（k）和原始信号的区别就越小，分解效果也就越差。然而一定存在一个噪声值，使RMSE最大，cmax（k）只包含原始信号的主要成分，并与噪声和其他无关的分量分开，这是理想的分解效果，对应的噪声幅值是最优的。因此，利用RMSE指标，可以确定适合的待添加噪声幅值。

如图1所示，以对电压暂降信号的分解为例，当噪声幅值为0.15时，所对应的RMSE值最大，分解效果是最好的，有效改善了模态混叠现象。

图1 最佳待添加幅值噪声选择

当最佳辅助添加噪声幅值选定好后，下一步就是选择最佳迭代次数，迭代次数越多，各IMF分量的残余噪声就越少，信噪比（SNR）就越高。因此，选用信噪比来衡量增加迭代次数的效果。如图2所示，当迭代次数小于200时，SNR值的增加非常明显；当迭代次数大于200时，SNR值的增加很缓慢。迭代次数越多，计算量就越大，综合考虑算法性能和计算代价，选定最佳迭代次数为200。

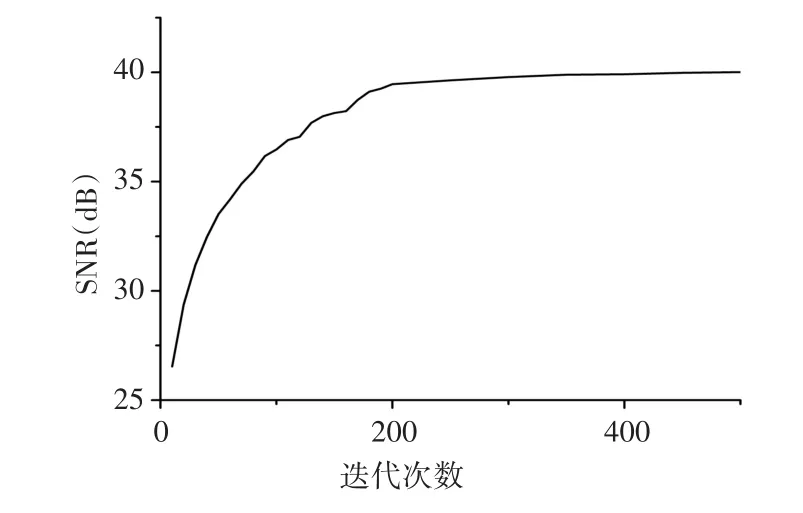
图2 最佳迭代次数选择

3 暂态电能质量扰动特征提取

3.1 信号模型

根据文献［3］提出的暂态电能质量扰动信号模型，对单一扰动，两种扰动复合进行识别分类，分别包括电压暂降、电压暂升、电压中断、暂态振荡、暂态脉冲和幅值变动的复合扰动、暂态振荡和幅值变动的复合扰动。采用Matlab生成扰动样本信号，设定采样率为8000Hz，扰动信号长度20个周波，基频频率为50Hz，共采集3200个数据。

3.2 特征提取

F1:信号经EEMD分解后，前三个IMF分量与原始信号的相关系数。不含电磁暂态的扰动经分解后前3个IMF分量主要成分为噪声信号，与原始信号相关性极低。暂态振荡持续的时间要比暂态脉冲长，经分解后，前三个IMF分量与原信号的相关性值大于暂态脉冲。经实验可知，当F1＜0.03时，可知待处理信号为幅值扰动；当0.03＜F1＜0.05时，待处理信号包含暂态脉冲成分；当F1＞0.05时，待处理信号包含暂态振荡成分。

F2，F3，F4:经EEMD分解后与原始信号相关性最大的三个IMF分量的标准能量差组成的特征向量。以此作为分类器的输入。标准能量差的公式如式（3）所示:

其中，Ni是第i个IMF分量，Ti是第一个IMF分量的标准能量差；Ci，EEMD（k）是扰动信号的第i个分量的第k个数据点；Ci，normal（k）是正常信号的第i个分量的第k个数据点。

其识别流程如图3所示。

图3 识别流程

4 暂态电能质量扰动分类

4.1 模糊C均值聚类方法

模糊C均值算法（fuzzy c-mean algorithm，FCM）是一种无监督动态聚类算法，能将多维空间中的数据样本｛x1，x2，…，xn｝划分为多个集群，j（2≤c≤n）是集群的数量，｛A1，A2，…，Aj｝表示相应的j个类别，每个集群都有自己的聚类中心｛v1，v2，…vj｝。

uij是样本xi对于Aj类的隶属度，隶属度的值反映了数据样本与集群的紧密程度，数据样本对每个类别的隶属度形成隶属度矩阵，用U=｛uij｝，uij表示第i个数据样本属于第j个类别的隶属度。则目标函数obj可以用式（4）表达:

1）随机生成一个隶属度矩阵；

2）分别根据式（5）和式（6）求得聚类中心和新的隶属度矩阵；

4.2 扰动分类仿真分析

采用Matlab仿真软件生成电能质量扰动信号，每类扰动产生20个随机样本，经特征提取后，产生20组特征向量作为测试集，将特征向量送入分类器进行分类，得出每一种扰动的聚类中心，如表1所示。

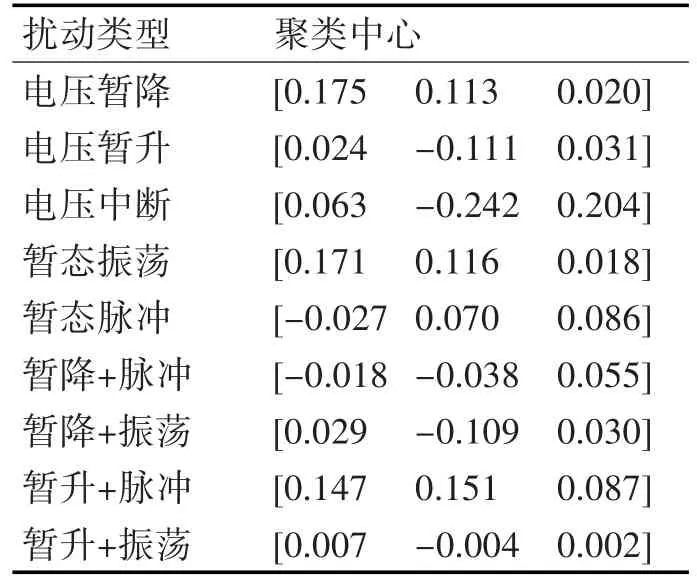
表1 各种扰动的聚类中心

经特征值F1将扰动类型分为3个组别，分别为幅值扰动、含暂态震荡的扰动和含暂态脉冲的扰动，每个组有三种类型的扰动。每种扰动随机产生3个未知样本扰动信号，每组共9个未知样本，根据隶属度来进行判别，对应隶属度最大的扰动，便归类于该扰动类型。如表2、表3、表4所示，加粗部分为样本属于某一类别时的隶属度。

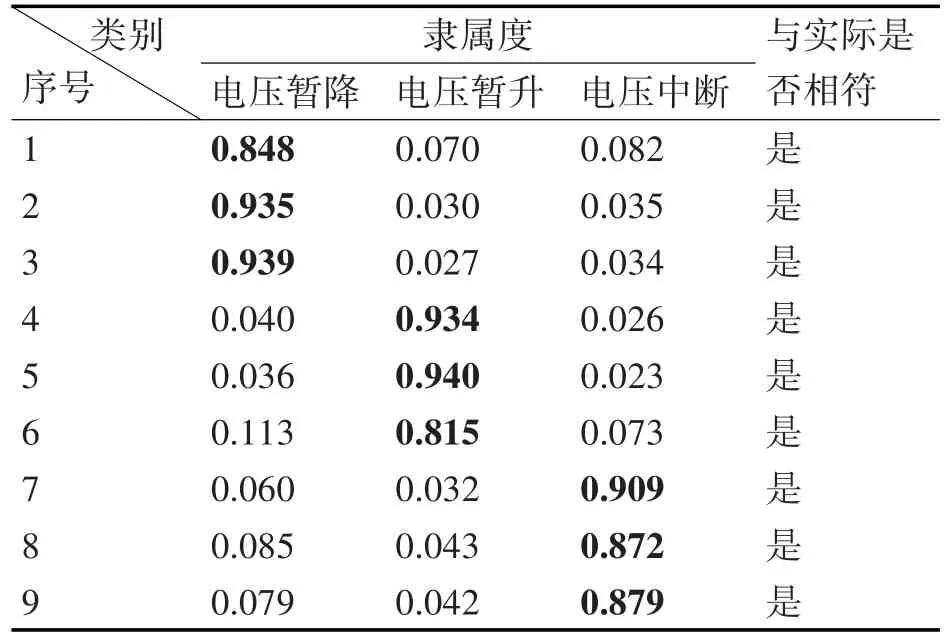
表2 判断未知样本是哪种幅值扰动

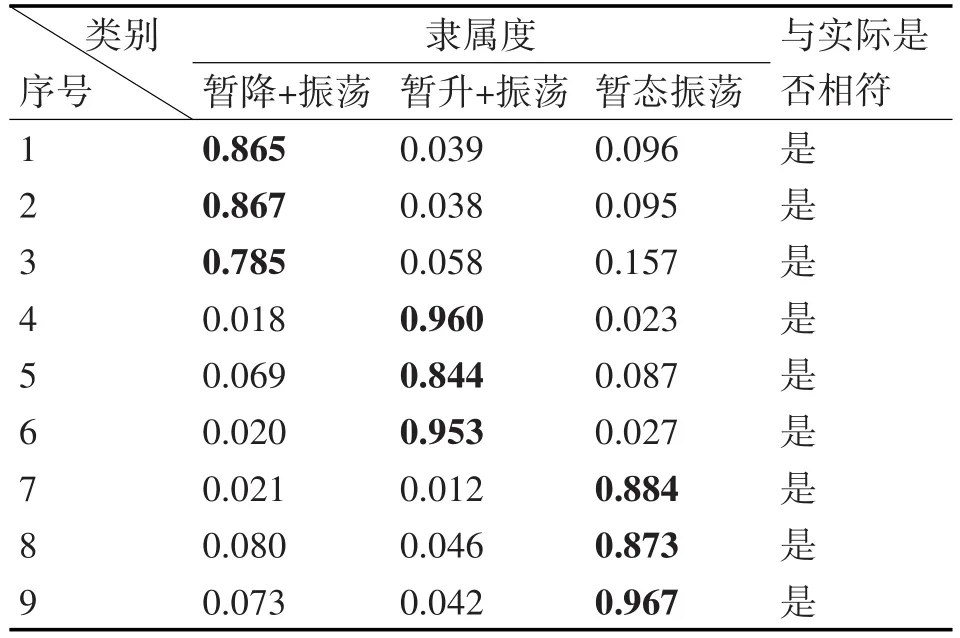
表3 判断未知样本是哪种暂态振荡扰动

表4 判断未知样本是哪种暂态脉冲扰动

5 结语

本文在通过合理设置EEMD方法的参数来进一步改善了传统EEMD方法的模态混叠现象，使待测信号经分解后保留更多的有用信息，结合FCM算法构建暂态电能质量识别系统。该系统易于实现，且识别速度快、精度高，抗干扰能力强。