高速无人驾驶车辆的操控稳定性研究*

2019-06-01陈慧岩龚建伟陈舒平

汽车工程 2019年5期

刘凯，陈慧岩，龚建伟，陈舒平，张玉

（北京理工大学机械与车辆学院，北京 100081）

前言

随着计算机信息处理技术和传感器技术的进步，基于高效环境感知的无人驾驶车辆技术迅速发展，并在军事及商业应用领域取得了长足的进步［1］。未来无人驾驶车辆发展的一个重要趋势是提高无人驾驶车辆的行驶速度，使之在高速条件下具有良好的稳定性和安全性［2-3］。然而，高速无人驾驶车辆的操控稳定性受到高度非线性的车辆动力学特性约束，特别是在低附着路面或存在复杂曲率的道路上行驶时，容易发生侧滑甚至导致车辆失控，严重威胁着无人驾驶车辆及乘员的安全［4］。因此，通过系统地考虑高速车辆的非线性动力学特性以及复杂道路条件的影响，研究高速无人驾驶车辆的操控稳定性，成为无人驾驶车辆发展的关键技术。

目前，模型预测控制由于具备能够系统地考虑模型非线性，且易于处理多约束优化问题等优势，在无人驾驶车辆的运动规划与控制等领域得到广泛的应用［5-6］。然而，模型预测控制方法通常依赖车辆本身的稳定性操控系统，如电子稳定控制（ESC）等来防止车辆失稳。这就导致经过车载系统调整后的轨迹无法保证车辆的无碰撞行驶。针对这一问题，将滑移包络线等车辆操控稳定性约束与模型预测控制相结合的轨迹跟踪方法被广泛用于保证无人驾驶车辆在接近速度极限下的行驶安全［7-8］。但该方法没有充分考虑地面附着力以及道路曲率对车辆操控稳定性的影响。此外，相较于常规速度，高速下的无人驾驶车辆需更长的预测时域和更高的实时性来保证行驶安全［9］。然而，使用非线性动力学模型描述车辆运动所导致的计算复杂度是阻碍其推广应用的重要原因。

针对上述问题，本文中在深入研究地面附着条件和道路曲率对车辆转向特性和稳定性影响的基础上，建立了考虑道路曲率的高速车辆等效动力学模型，并提出一种变步长的模型离散化方法，能在保证车辆模型预测精度的基础上，实现较长的预测时域，并满足计算实时性的要求。通过分析车辆稳态行驶时的最大横摆角速度和轮胎最大侧偏力，得出了高速无人驾驶车辆滑移稳定的约束条件，并得出了车辆在道路内行驶的环境约束条件。最后将在高速和滑移等复杂约束下的无人驾驶车辆操控稳定性操控问题转化为二次型优化问题，并运用模型预测控制算法实时计算满足约束条件的车辆无碰撞运动轨迹及控制序列，从而保证车辆行驶安全与操控稳定性。

1 车辆动力学建模

高速车辆的等效动力学建模是研究其轨迹跟踪控制及操控稳定性的基础。考虑道路曲率对高速车辆转向特性和行驶稳定性的影响，建立高速车辆等效动力学模型，如图1所示。

考虑高速行驶的特性，车辆前轮偏角δf和车辆与参考路径之间的航向角偏差eψ采用小角度假设，车辆的动力学模型为

图1 车辆动力学模型

式中：vx，vy分别为车体质心处的纵向和横向速度；Fyf，Fyr为前轮和后轮的侧向力；r为车体航向角变化率；m为车辆质量；Iz为车身绕z轴的转动惯量；κ为参考道路的曲率；lf，lr分别为车辆质心到前轴和后轴的距离；ey为车辆与参考路径的横向距离偏差；ψ和ψr为车体航向角和参考路径切向角。式（1）中的非线性因素主要来自轮胎侧向力，本文中采用Pacejka提出的Brush轮胎模型［10］计算轮胎侧向力Fy：

式中：α为轮胎侧偏角；Cα为轮胎的侧偏刚度。

当路面的摩擦因数μ及轮胎垂直载荷Fz确定后，轮胎侧向力Fy可简化为轮胎的等效侧偏刚度与轮胎侧偏角α的线性模型：

由于此线性轮胎模型只在轮胎侧向力的线性区域内有效，如图2所示。因此，在应用中需要限制轮胎侧偏角的阈值αt。轮胎的侧偏角α和等效侧偏刚度¯可通过实时参数估计方法得到［11］。

图2 轮胎侧向力与侧偏角的关系

式中：h为车辆质心相对于底盘的高度；ax为车辆的纵向加速度。

通过小角度假设可近似得到车辆前后轮胎的侧偏角 αf和 αr：

综合式（1）～式（7），令 ξ=［vyr eyeψ］T为状态向量，u1=δf为控制输入量，u2=κ为附加输入，可得到考虑道路曲率和路面倾角的高速车辆等效动力学模型：

2 变步长的模型离散化方法

由于高速时的无人驾驶车辆轨迹跟踪比常速时需要更长的预测时域来应对环境变化，因此车辆动力学模型的离散化方法对车辆控制算法的实时性至关重要。然而，确定模型离散化的采样步长仍然是一个挑战，不论采用较大还是较小的采样步长，都有各自的优缺点：使用较小的采样步长可使得系统的控制效果更好，但由于预测步数的增多使得控制系统的运算效率降低；而采用较大的采样步长则需要以牺牲一定预测精度来实现较长的预测时域。考虑到高速无人驾驶汽车轨迹跟踪对于模型预测精度、计算实时性和车辆操控稳定性都有较高的要求，所以单一固定的采样步长已无法满足实际需求。

针对这一挑战，本文中采用变步长的离散化方法来实现较长的预测时域，并保证离散后车辆动力学模型的预测精度和计算实时性。此模型离散方法将整个预测时域分成两部分：第一部分使用短步长ts进行离散以保证离散后模型的精度；第二部分使用较长的步长tl进行离散，在合理的模型精度和计算量下实现较长的预测时域。设整个预测时域为Np，并在第Ns步分成短步长离散和长步长离散两个部分。

第一部分，k=0，…，Ns，将式（8）表示的车辆动力学模型以ts为步长，使用0阶保持（ZOH）进行离散。首先设计增广向量 zs=［ξ，u1，u2］T，则式（8）可表示为

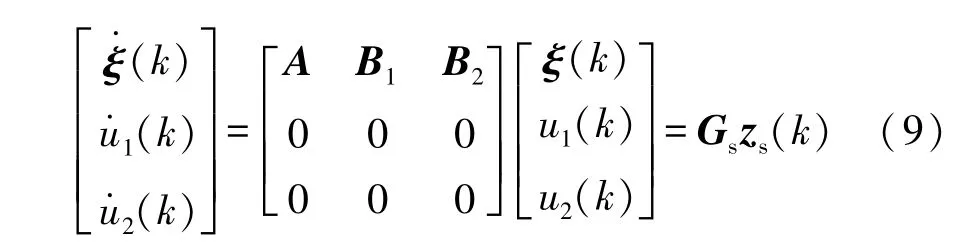
式（9）通过对Gsts进行矩阵指数函数计算，并采取0阶保持可得

根据不同离散步长使用不同的模型离散化方法的对比如图3所示。

图3 变步长的模型离散化方法对比

图3中带圈虚线为一组期望的控制器输入量，带星号的实线为式（11）离散模型的输入。可看出这种离散方法能够比较精确地符合期望的控制输入量，这是因为车辆的底层控制器也会在1个控制周期ts内保持控制量恒定。然而，0阶保持对于第二部分k=Ns＋1，…，Np则不再适用，因为在0阶保持会限定这部分的控制量在较长的预测周期tl内保持不变，如图3中点划线所示。可看出该假设会使得模型输入与期望的控制产生较大的偏离，因为控制量在一个较长时间内可能会有比较显著的变化。针对这种情况，1阶保持通过假设控制量在预测周期tl内呈线性变化，有效地适应了较长的离散步长，提供了更好的长步长离散化方法，如图3中短虚线所示。虽短虚线仍无法与带圈虚线重合，但在控制精度可接受的范围内。因此，将预测时域的第二部分（k=Ns＋1，…，Np），以 tl为步长，使用 1阶保持（FOH）进行离散。

3 基于MPC的轨迹跟踪控制器

3.1 滑移稳定性约束

车辆滑移主要是由轮胎变形产生侧偏角导致的，本文中将轮胎侧偏角限制在［-αt，αt］，以保证线性化轮胎模型的有效性。根据对后轮侧偏角的限制推导车辆的滑移稳定性约束。后轮最大侧偏角限制可以由式（7）转化为对车辆横向速度vy和航向角变化率r的约束

式中航向角变化率的阈值可根据后轮最大侧偏力及式（1）获得：

式（15）和式（16）约束组成了一个封闭的包络线，如图4所示，其中，①和③代表的是式（15）约束，②和④代表的是式（16）约束。当车辆状态处于包络线之内，车辆满足滑移约束。然而，车辆状态超出包络线并不必然导致车辆失稳，例如当后轮侧偏角超出阈值，后轮侧偏力进入轮胎模型的非线性区域，虽然轮胎力的线性化条件失效，但短时间内仍能保持车辆的可控性。因此，设置了约束松弛因子允许车辆状态暂时超出包络线的限制，优先保证车辆的无碰撞轨迹。

3.2 道路环境及执行机构饱和约束

图4 高速车辆滑移的包络线约束

道路环境对高速车辆的约束主要表现为车辆轨迹须保持在给定的可行区域内，并满足无碰撞的要求。高速车辆避障功能可通过在生成可行区域时考虑障碍物的影响来实现。本文中将道路环境对车辆轨迹的约束表示为一系列横向偏差阈值的组合，如图5所示。

图5 道路环境约束

首先根据车辆纵向速度和车辆动力学模型的离散化步长，在道路的纵向上生成一系列参考点。然后将道路环境约束对参考点的横向跟踪偏差阈值定义为 emax（k）和 emin（k），因此道路环境约束为

式中：ξ（k）为车辆在第 k时刻的状态；ds为一个根据车体尺寸定义的安全距离。

此外，高速车辆的跟踪控制须满足底层驱动力的限制，设 δf，max和 Δδf，max分别为前轮偏角及其变化量的阈值，则

3.3 模型预测控制问题

考虑滑移和侧倾的高速无人驾驶车辆运动规划与跟踪控制问题可转换为式（21）的二次型最优求解问题，并通过实时求解生成有效避险的运动规划轨迹及最优控制序列，同时防止车辆侧滑危险的发生。模型预测控制中所涉及的变量及其数值如表1所示。

表1 模型预测控制使用的参数及其数值说明

式中待优化的变量是车辆前轮偏角控制量δf和滑移约束的松弛因子Ssh。松弛因子的存在是为了通过允许高速车辆出现暂时性滑移现象以保证此优化问题始终存在可行解。需要调试的参数为Wδf，Wey，Weψ和松弛因子的权重 Ws，通过选取不同的权重可以体现出优化目标的优先级。对车辆滑移约束施加一定的松弛因子，可保证当道路的无碰撞轨迹与稳定性约束发生冲突时，优先保证车辆在可行区域内行驶，即允许车辆暂时发生滑移。

式（21）中：式（21a）抑制了高速无人驾驶车辆相对于参考路径的横向偏差和航向偏差，体现了路径跟踪的期望；式（21b）建立了跟踪参考路径与控制量平滑之间的关系；式（21c）对车辆滑移稳定性约束的松弛因子进行惩罚，促使高速车辆尽量不出现滑移现象；式（21d）和式（21e）分别为变步长离散方法得到的车辆动力学等效模型；式（21f）和式（21g）分别为针对高速车辆行驶过程中稳定性的包络线滑移约束和道路环境约束；式（21h）和式（21i）体现了对车辆执行机构和底层驱动能力的约束。

本文中使用 CVXGEN［12］生成针对求解式（21）二次型优化问题的求解器，优化得到前轮偏角的最优控制序列，模型预测控制使用的参数说明见表1。

4 仿真试验研究

为验证本文中所提出的控制器保持高速无人驾驶车辆操控稳定性的能力，并保证仿真研究的充分性，在多种道路条件和车速下进行对比仿真试验，分别选取干燥的沥青路面、潮湿的沥青路面和冰雪覆盖的路面等3种典型道路。不同道路摩擦因数的取值根据文献［13］中获得。通过CarSim／Simulink搭建联合仿真试验环境，仿真测试道路包含3个连续大曲率弯道，如图6所示。仿真所用车辆模型的各项参数如表2所示。

图6 CarSim／Simulink联合仿真测试道路

4.1 干燥的沥青路面

干燥沥青路面的摩擦因数设为0.85，分别以70，80，90和100 km／h的车速进行仿真试验，试验结果如图7所示。图7（a）为高速无人驾驶车辆的横向跟踪误差对比图，7（b）为轨迹跟踪控制器优化得到的前轮转角控制量，7（c）为轨迹跟踪过程中车辆质心横向速度及横摆角速度的对比图。

表2 车辆参数及其数值说明

由图7（a）可知，高速无人驾驶车辆的横向跟踪偏差始终保持在0.5 m以内。图7（b）则显示，无论在何种速度，控制器优化得到的前轮转角都处于执行机构的机械饱和约束范围内。由图7（c）可知，被控车辆的车辆质心横向速度及横摆角速度始终处于滑移包络线之内，即高速车辆处于操控稳定性的状态，而且车速越低，车辆越稳定，与实际规律相符合。仿真结果验证了本文中提出的轨迹跟踪控制器在干燥沥青道路下的有效性。

4.2 潮湿的沥青路面

潮湿沥青路面的路面摩擦因数设为0.6，仿真测试车速分别为60，70，80和90 km／h，试验结果如图8所示。

高速无人驾驶车辆的横向跟踪偏差对比图如图8（a）所示，可以看出当车速低于95 km／h时，被控车辆的跟踪误差始终保持在0.5 m以内，即始终行驶在给定的道路区域内。然而，当车速高于95 km／h时横向跟踪偏差会超过道路环境约束。这种情况发生主要是由于当车速过高时，潮湿地面所能提供的附着力不足以约束车辆的横向滑移所导致的。

跟踪控制器优化得到的前轮转角如图8（b）所示，满足转向机构的机械饱和约束。被控车辆的车辆质心横向速度及横摆角速度的轨迹如图8（c）所示，当车速低于95 km／h时被控车辆的横向速度和横摆角速度仍然处于滑移包络线之内，但是当车速高于95 km／h时滑移包络线约束失效，车辆发生失稳。综上可知，本文中提出的高速车辆轨迹跟踪控制器可在一定速度下有效地控制车辆安全地行驶在潮湿的沥青路面上，具有较为令人满意的控制效果。

图7 干燥沥青路面上的路径跟踪仿真结果

4.3 冰雪覆盖的路面

在冰雪路面上进行仿真试验可更为有效地检验本文中提出的方法保证高速无人驾驶车辆操控稳定性的能力。冰雪覆盖道路的路面摩擦因数设为0.3，仿真车速分别取为 50，60，65和 70 km／h，仿真结果如图9所示。可以看出，本文中设计的路径跟踪控制器在冰雪路面上仍具有较好的控制效果，能够以一定的速度在较低的路面附着系数下实现被控车辆安全稳定地行驶。但是当车速超过65 km／h后则不能保证车辆在冰雪路面的稳定行驶。