优化的Gray Markov模型在埋地管道腐蚀速率预测中的应用

骆正山，陈 晨，王 哲

（西安建筑科技大学管理学院，西安710055）

管道运输是石油运输的重要方式，其集输系统是一种具有高度危险性的连续运输系统［1］。油气管道在运行一定时间后因腐蚀穿孔而导致的油气泄漏，不仅消耗了宝贵的资源，干扰了整个输送系统的正常运行，还会对周围环境造成较大危害。因此，管道腐蚀问题成为了腐蚀研究领域的重中之重［2］。对管道进行安全评估是减少管道事故的有效方法，对油气管道的腐蚀速率和油气管网的腐蚀状态进行预测，能为管道的风险评价提供可靠的理论依据，从而制定出适当的防护措施，节省管道的维修费用，降低经济损失。目前，油气管道的腐蚀预测已成为确保油气管网安全运行的有效手段。

管道腐蚀的影响因素众多，腐蚀速率随机波动性大且存在一定增长趋势。灰色马尔科夫预测模型擅长解决此类问题，无需大量历史数据，在短时间内可以得到较为精确的预测值，因此在很多领域得到了广泛应用［3-5］。近年来对灰色马尔科夫链模型的改进方法也层出不穷，对在役飞机结构使用寿命进行预测时，张晓春等［6］提出了灰色马氏链二次残差修正技术，建立灰色残差模型修正经典灰色模型后，使用两种方法修正一次残差修正模型的预测值，并取其相对误差最小的值。周建等［7］将BP神经网络与灰色马尔科夫模型相结合，通过训练神经网络选取影响最大的因素，实现从大样本到小样本的转化。张新生等［8］在对管道腐蚀深度进行预测的过程中，对马尔科夫模型的状态转移矩阵进行改进，建立滑动转移状态概率矩阵，充分考虑信息的全面性和实时性，提高了预测精度。但是在众多改进方法中，少有综合模型远期预测时效和动态预测的改进方法。

为进一步提高预测模型对随机波动性较大的管道腐蚀速率的中长期预测精度，本工作采用一种多角度优化的灰色马尔科夫动态模型来预测管道的腐蚀速率，以期为管道风险评估方法的选择提供参考。

1 灰色预测模型

1.1 传统灰色预测模型

灰色系统预测适用于数据少但系统状态基本连续条件下的预测［9］。管道腐蚀变化的过程是一个随机过程，管道腐蚀速率可视为一个灰色系统。基于灰色系统的理论基础，将管道腐蚀速率实测数据进行分析计算，生成有规律的新数列进行未来一段时间内管道腐蚀程度及速率的预测，形成一系列时间序列问题，其实质描述了系统的宏观发展规律。

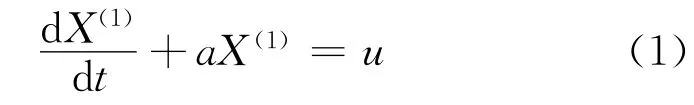
其中，X（1）＝｛，……，｝，是在不同检测时间检测到的在役管道腐蚀速率原始数据序列X（0）＝，……｝的一次累加生成算子序列，而x（1）（k）表示k次检测之前油气管道腐蚀速率累计量，满足：

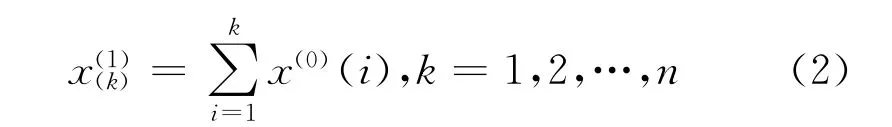
其紧邻生成序列为：

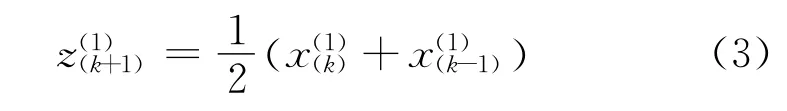
由上式建立矩阵，通过最小二乘法求得灰参数a，u：

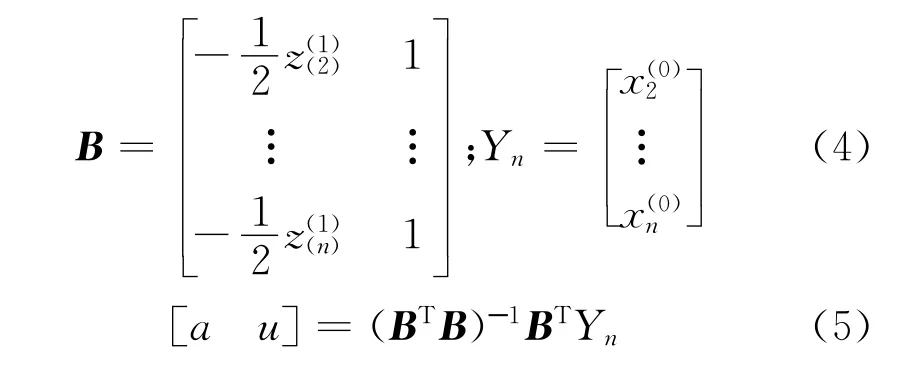
则油气管道腐蚀速率灰色GM（1，1）预测模型的响应式为：

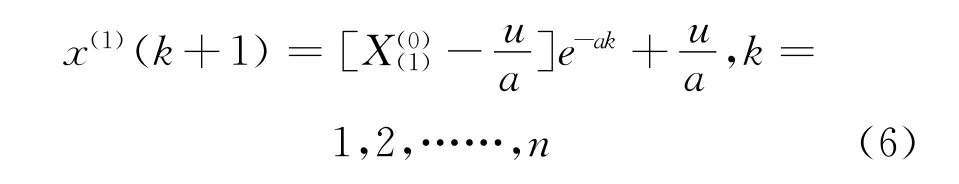
将上式进行累减还原，得到数据序列预测值，即：

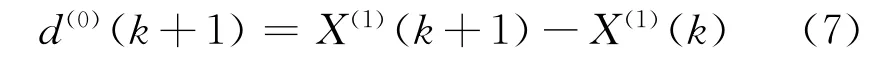
1.2 灰色预测模型的优化

传统灰色模型已被广泛运用于各领域的短期预测中，且在运用传统灰色模型进行预测时，对具有一定规律增长趋势的光滑数据序列可以预测出事物发展的总体趋势。而随着时间的变化，未来时刻的不确定性因素将对系统造成影响，对于预测期远、波动性较大的数据，后期预测难以达到较高的精确度。为提高模型的精度和使用效率，提出如下改进方法［10］：

（1）背景值优化

灰色模型对原始数据的要求比较低，为保证不改变原始序列的增长趋势，提高原始数据的光滑度，根据差分插值原理对预测模型背景值序列进行优化，因此采取对数变换原始数据：

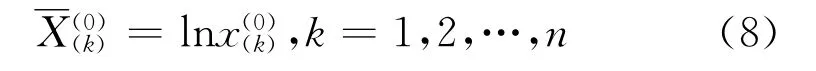
得到精确度更高的预测结果之后再进行对数逆变换即可得到原始数据的预测值。

（2）无偏灰色模型

为消除灰色模型在拟合指数增长序列时存在的偏差，引入无偏灰色模型来进行修正，设原始数据序列为严格的指数序列，则有：

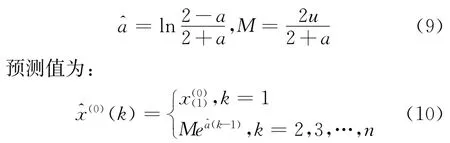
无偏灰色模型无需再进行累减还原，在消除传统灰色模型故有偏差的同时简化了计算步骤［11］。

（3）等维新信息模型

灰色预测模型的预测时效具有局限性，模型后期预测时预测值的偏差会逐渐增大，波动性大的数据难以高度拟合。在此引入一种等维新信息模型，即在保持序列维数不变的同时，更新原始数据进行预测。获得k+1时刻预测值后，去掉原始数列中的，加入新的实测值，重新构成初始预测序列｝，建立新的GM（1，1）模型，预测k+2时刻的腐蚀速率值。按此方法逐个预测进行替补，称为等维新信息预测模型［12］。对于远期预测问题，为提高模型预测时效和动态拟合精度，在模型建立完备后，可对其进行动态调整。

2 马尔科夫预测模型

2.1 传统马尔科夫预测模型

油气管道的腐蚀速率实测值与预测值之间存在较大的残差，管道腐蚀速率累积量的灰色预测精度较低［13］。因此，将管道腐蚀速率预测值的残差状态看作马尔科夫决策过程，根据未来时间段内预测值残差状态之间的转移概率，来预测未来时刻残差状态的发展趋势，以此来修正灰色模型的预测值，提高模型的预测精度。根据等概率原则，将灰色模型计算得出的油气管道腐蚀速率预测值的残差状态，划分m个状态区间Im。

设有随机过程｛Xn，n∈T｝，对任意的整数｛n∈T｝和任意的i0，i1，……，∈I，I为离散值的状态空间。若状态空间是有限或可数的，且条件概率满足［14］：

则称｛Xn，n∈T｝为马尔柯夫链或马氏链。

根据油气管道腐蚀速率预测值残差数列的状态，利用频数统计分析的方法来确定其一步状态转移概率矩阵P。

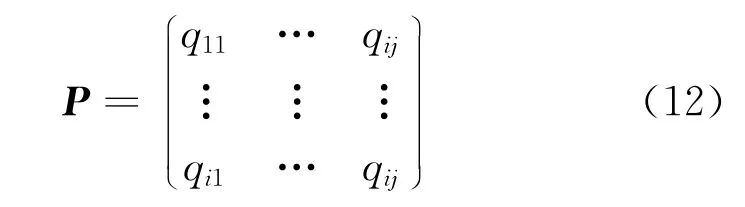
而状态转移概率qij满足行元素和为1∶0≤qij≤1，i，j＝1，2，…，n。且qij＝gij／gi，gi表示状态Im出现的频数，gij表示状态i转移到状态j的频数［15］。

假设系统处于某一时刻的初始状态为S（0），系统由初始状态开始进行变化发展，经过n步变化之后，发展到另一状态Sn。根据Chapman-Kolmogorov方程计算：P（n）＝P（n）P＝P（n）可求出n步状态转移矩阵Pn，状态Sn根据式Sn＝S0P（n）＝S0Pn计算［16］。预测期望为：

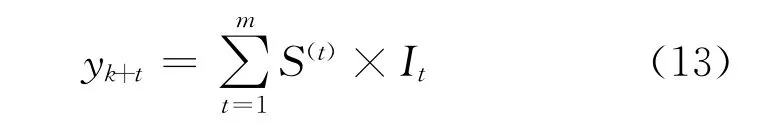
其中，It取状态区间的中值。由上述计算步骤可知，预测值为：

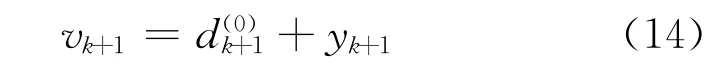
2.2 马尔科夫预测模型的优化

马尔科夫链模型预测是通过计算系统中各状态之间的转移概率来实现的，转移概率反映的是各随机因素之间的相互关系［17］。而马尔科夫链的状态转移概率计算和状态区间的取值对预测结果十分重要，选取适当的模型参数值求解方法，才能准确预测系统行为的变化，发挥马尔科夫链模型的超前预测作用，提高整体模型预测能力的准确性和实时性。为此，提出以下改进：

（1）二次平滑指数法优化

在计算状态转移的Sn＝S0P（n）过程中，运用初始状态预测下一步状态发展趋势时，若不考虑各时间段权重对预测结果的影响，时间序列会在某种程度上被合理顺延，将会导致预测结果的误差偏大。将最大的权重放在最近的计算数据状态中，能减少这种滞后偏差，因此采用二次指数平滑法对状态转移过程进行改进，变换如下：

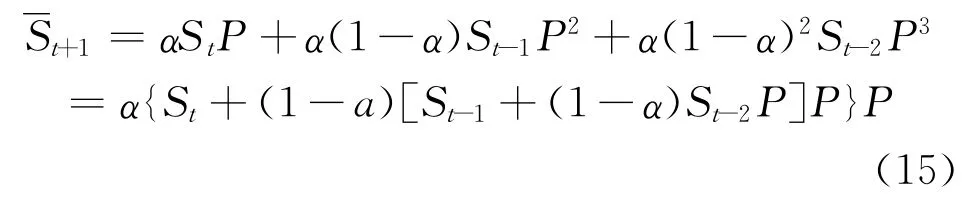
（2）粒子群算法优化状态区间白化系数

在计算预测值期望yk+1＝×It的过程中，会取残差序列的i个状态，It取区间的中值，但是在实际应用过程中，中间值不一定是最优的选取结果，即灰区间的白化系数λ的最优取值不一定是0.5。为了求解残差序列中的最优残差预测值，采用粒子群算法对白化系数λ进行优化，该方法过程简单且全局搜索能力强，过程如下［18］：

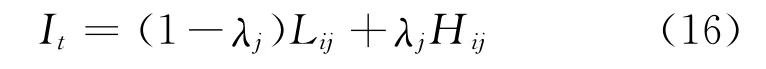
Lij和Hij的上下边界值λ取值为［0，1］。

粒子群算法可通过Matlab编程来实现，采用均方差衡量每个粒子的适应度函数，可以得到残差序列状态转移状态中出现的概率最大的点。

3 实例分析

以某公司气田某段油气管道（φ720 mm×8 mm）为例，在不同时间检测得到的腐蚀速率监测数据如表1所示。

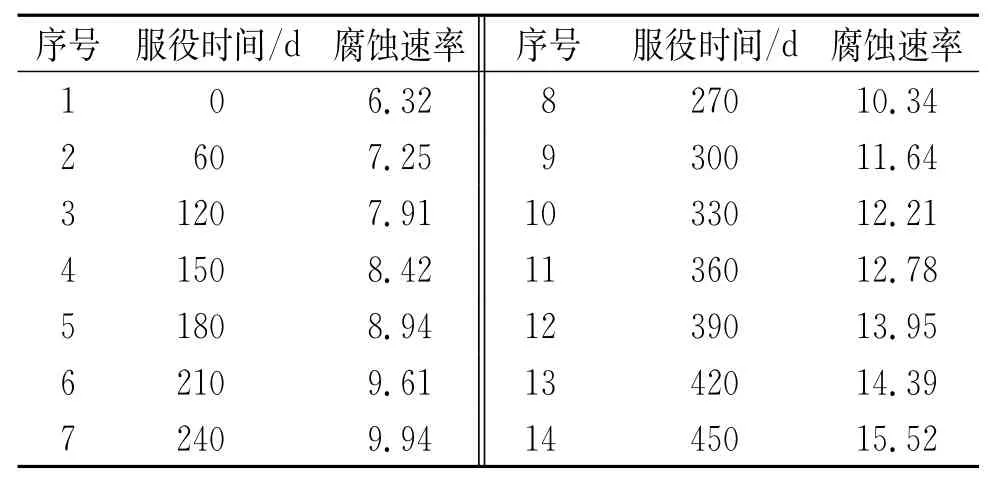
表1 管道在服役不同时间测得的腐蚀速率Tab.1 Corrosion rates of pipelines run for different times×10-2 mm／a

根据前述模型，先以管道腐蚀速率原始值进行优化的灰色模型预测。通过数据序列的前11个数据对序号为12、13、14的数据进行预测比较。将数据进行对数处理，提高原始数据光滑度后，取测量值的前5个数据为第一组原始数据，建立灰色无偏预测模型。以此为基础进行等维新信息预测，实时删去第一个原始数据，添加下一个实测值进行新一轮预测，求出下一时刻的预测值。最终将数据进行对数还原。预测结果见表2。

对上述优化的GM（1，1）预测模型进行精度检验，c≈0.215 7，p＝1，结果表明该模型具有良好的精度，可用于油气管道管壁腐蚀速率的预测。由灰色模型得到的管道腐蚀速率预测的宏观值，转入马尔科夫模型进行残差修正［19］。通过计算得出残差值，对管壁的腐蚀速率残差状态进行划分，分为四个状态，管壁腐蚀状态的划分结果见表3。

由表3可得各状态的转移规律，得到一步转移矩阵P（1）。

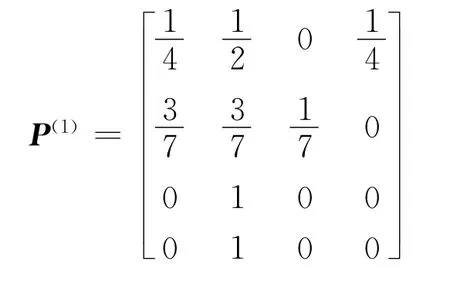
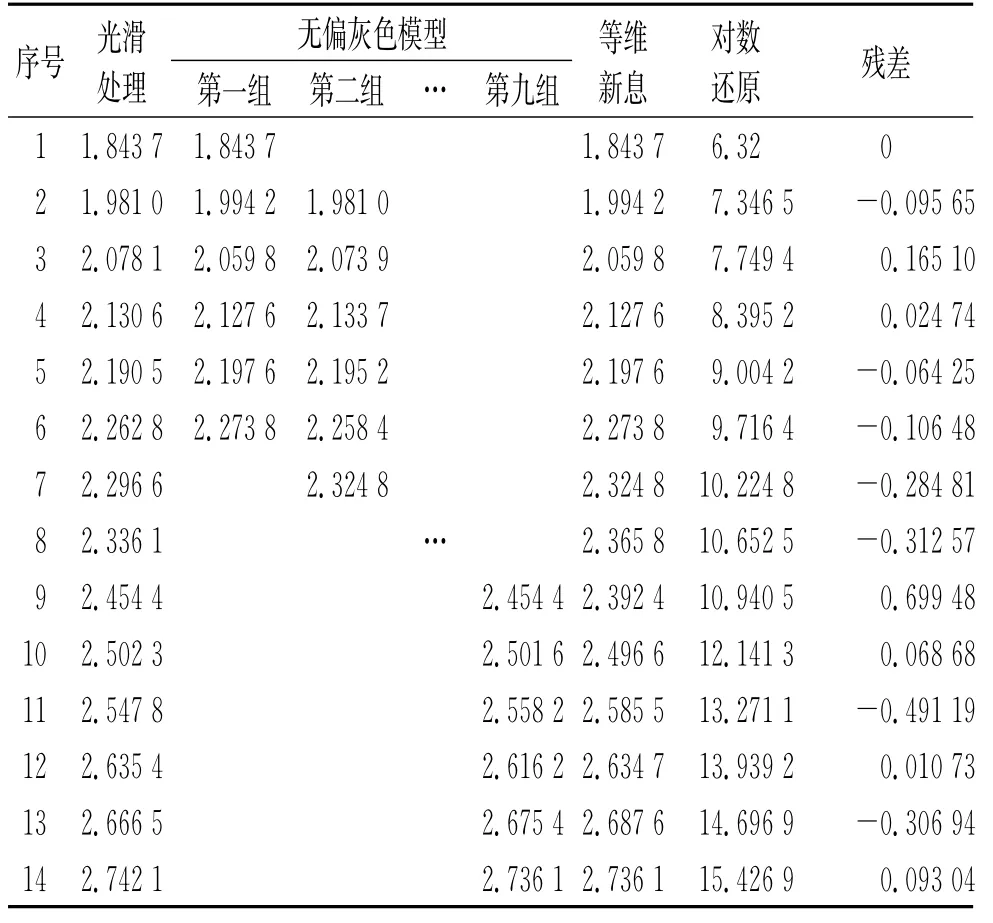
表2 优化灰色模型的预测结果Tab.2 Prediction results of optimized grey model

表3 管道腐蚀状态的划分结果Tab.3 Division results of pipeline corrosion states×10-2

在excel中运用指数平滑数据分析方法可得：当平滑指数α＝0.95时，绝对误差最小，因此，选取此值作为最终指数平滑系数，进行二次平滑处理。取第5号数据为初始状态S0＝［0，1，0，0］，3，4两个时刻的状态分别为［0，0，1，0］、［0，1，0，0］，由式（14）可逐一计算6～14号数据残差的转移状态，预测结果见表4。

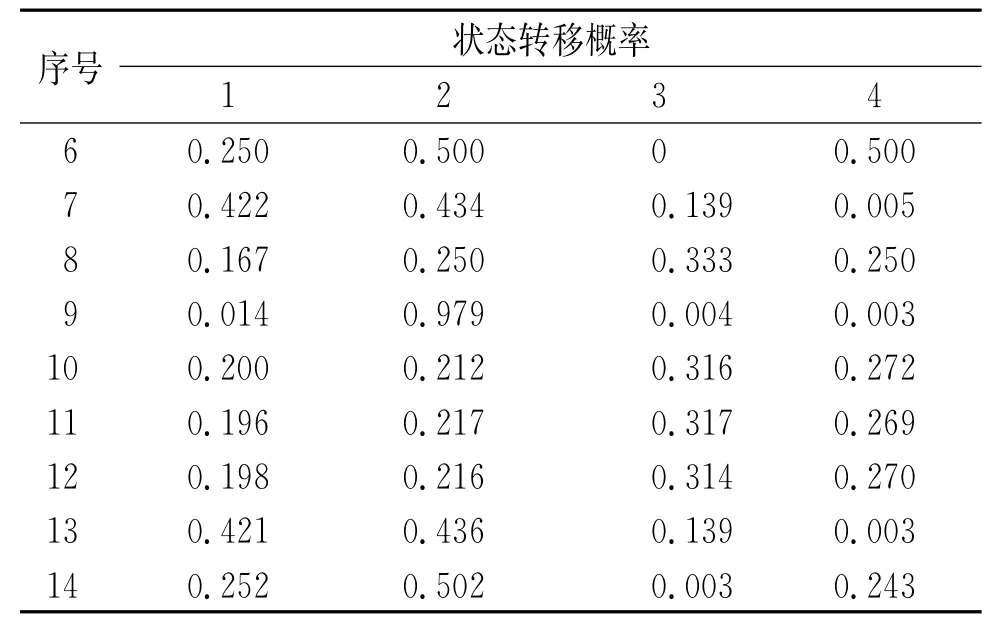
表4 管道腐蚀状态分布概率预测值Tab.4 The prediction of distribution probability of pipeline corrosion states

对于马尔科夫状态区间模型中的参数λ，应用可视化编程语言Matlab进行粒子群算法过程，根据前述模型设置各参数值，其中选取粒子长度为4，粒子数为300，c1＝0.6，c2＝0.8，ω＝0.005，进化代数K＝500、粒子更新位置最大为1最小为0。最终得到粒子最优位置，从而得到白化系数：λ1＝0.891，λ1＝0.132，λ1＝0.582，λ1＝0.916。由式（16）可得，残差状态转移中出现概率最大的点分别为：I1＝-45.866，I2＝6.482，I3＝22.854，I4＝42.681。

结合表4与计算得出的Im值，可根据式（13）求出残差预测值，对管道腐蚀速率预测值进行微观调整，最终与灰色模型的宏观预测值相加得出管道腐蚀速率预测值。篇幅有限，计算过程不一一列出。在说明该方法有效性的同时，建立传统灰色马尔科夫管道腐蚀速率预测模型用于比较，结果见表5。

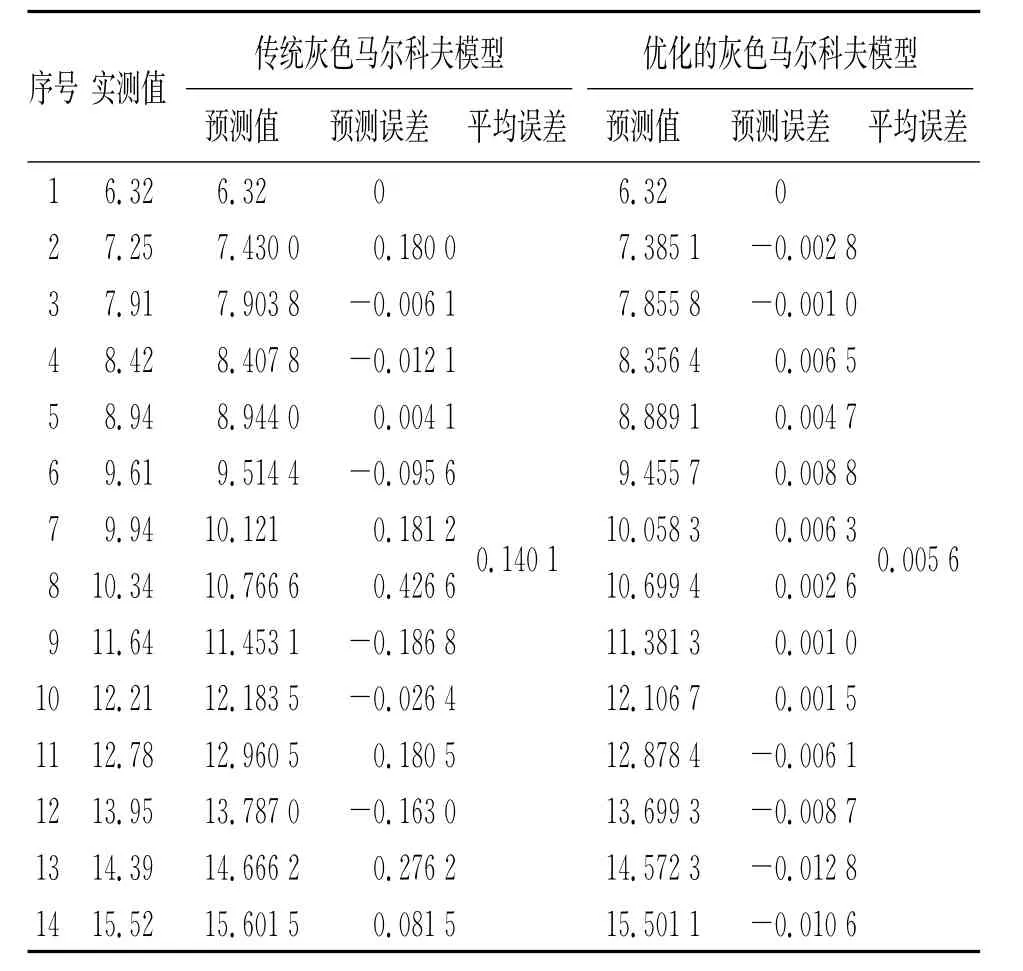
表5 两种模型预测结果的比较Tab.5 Comparison of prediction results of two models

由表5可见：优化的灰色马尔科夫模型（Model 1）的预测结果平均精确度比传统马尔科夫模型（Model 2）的提高了40.33%，绝对误差小，尤其是对于中长期预测，如12、13、14号数据的预测结果，与原模型相比有着更高的吻合度。

4 结论

（1）应用优化的灰色马尔科夫链动态模型预测管道腐蚀速率，既可以总体预测管道腐蚀速率发展的宏观趋势，又可以修正预测值的残差，描述管道腐蚀速率的微观变化，相比于传统的灰色马尔科夫预测模型，克服了动态预测的偏差性，并且其远期预测结果更加精确，能更好地满足现实工程对管道预测精度的实际需要。

（2）该方法适用于一切具有某种变化趋势、随机波动性大的中长期事件的预测评估，可使建模和预测结果更加有效、可靠，具有更高的拟合度，在动态预测模型中是一种实用性强的方法。通过对实际埋地管道腐蚀数据进行建模和预测，应用大量优化的灰色马尔科夫动态预测模型对管道腐蚀速率进行预测，可以及时且准确地掌握管道腐蚀情况，为埋地管道的进一步维护、检修与更换提供参考依据。