立方体α-Fe合成及其含量对吸波性能的影响*
2019-05-31史桂梅孙丽伟
史桂梅, 董 微, 孙丽伟
(沈阳工业大学 理学院, 沈阳 110870)
近年来,随着电子通讯与微波技术的快速发展,多样化的电子产品逐渐融入生活,给人类带来了极大的方便.然而电磁污染也随之而来,成为人类面临的又一大环境问题[1],因此,吸波材料的研究日益广泛.随着隐身技术的发展,对高性能吸波材料的需求日益增加.在诸多吸波材料中,具有形状各向异性的磁性吸波材料可以突破传统吸波材料的Snoek极限[2],提高其磁导率和共振频率[3],因而已经成为新一代吸波材料的一个重要研究方向.
目前为止,研究者们已经研究了许多具有不同形状的磁性纳米复合吸波材料,如核壳型鱼骨状Cu@Ni、片状三角形Fe3O4、薄片软磁性羰基铁[4-6]等,这些吸收剂呈现出较好的吸波性能.理论分析与实验研究表明,磁性纳米微粒的微波吸收特性与其形貌密切相关.然而,目前关于形状各向异性吸波材料的研究多数局限于吸收剂含量唯一时吸波性能的报道.事实上,微波吸收特性可以通过调控吸收剂的含量进行改变[7].本文讨论了形状各向异性对吸波材料微波吸收性能的影响,在此基础上通过改变吸收剂的含量进一步讨论了吸收剂的不同含量对吸波性能的影响,同时也对吸波机制进行了分析.利用溶剂热法成功合成了立方体状α-Fe粉体.与之前报道的球形羰基Fe粉和球状磁性纳米Fe粉相比,当吸收剂质量分数为50%时,立方体状α-Fe粉的吸波性能要远优于球形羰基Fe粉和球状磁性纳米Fe粉[8].
1 实 验
1.1 实验试剂
实验所用化学试剂如表1所示.

表1 实验所用化学试剂Tab.1 Chemical reagents used in experiments
1.2 立方体状α-Fe制备
利用溶剂热法合成立方体状α-Fe粉体.将1.6 g FeSO4·7H2O与43 mL乙二胺在室温条件下溶解并进行磁力搅拌,待溶液颜色由浅绿色变为深棕色时,向溶液中加入14 mL水合肼并继续搅拌,直至溶液变为浅粉色后停止搅拌.随后向溶液中加入2.9 g氢氧化钠,将反应溶液转入反应釜并移入鼓风干燥箱中,设定相应的反应温度与时间.待反应结束后,将反应后所得产物利用无水乙醇与去离子水分别洗涤多次得到黑色粉末,之后将其转入真空干燥箱进行干燥后得到最终产物.立方体状α-Fe的合成流程图如图1所示.

图1 立方体状α-Fe的合成流程图Fig.1 Flow chart of synthesis of cube α-Fe
1.3 性能表征与测定
采用Miniflex600型X射线衍射仪(波长为0.154 05 nm)对样品的晶体结构进行测试.利用Phenom ProX型扫描电子显微镜、Tecnai G2 20ST型透射电子显微镜对样品形貌进行表征.采用RIBELAS-3000MK-2XPS型X射线光电子谱仪测定样品表面的组成成分.采用Agilent ENA5071C型矢量网络分析仪对样品的吸波性能进行测试.
2 结果与分析
2.1 立方体状α-Fe相结构
不同实验条件下所合成样品的XRD图谱如图2所示.
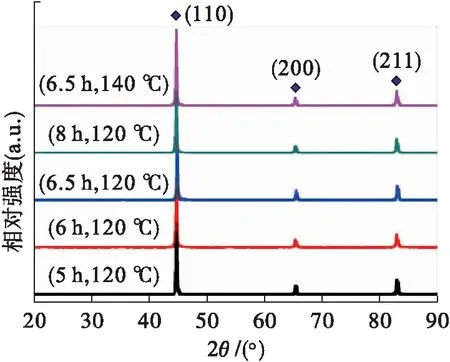
图2 立方体状α-Fe的XRD图谱Fig.2 XRD spectra of cube α-Fe
合成样品的反应时间分别为5、6、6.5、8 h,反应温度分别为120、140 ℃.由图2可见,不同反应条件下样品的XRD图谱均有3个衍射峰,对应的晶面指数分别为(110)、(200)和(211),表明样品只有α-Fe相,没有其他相.对照87-0721号JCPDF卡片后发现,样品为体心立方结构,表明所选的反应时间与反应温度对样品的相结构未产生影响.
2.2 反应时间对α-Fe形貌的影响
图3为当反应温度为120 ℃时,不同反应时间下所合成样品的SEM图像.由图3a可见,当反应时间为5 h时,大部分晶粒呈现出尺寸不等的多面体形状;由图3b可见,当反应时间为6 h时,已经可以观察到立方体状晶粒,但粒径大小不一,晶粒尺寸范围为200~400 nm;由图3c可见,当反应时间继续增加到6.5 h时,所合成α-Fe晶粒粒径均匀,尺寸约为350 nm,晶粒表面平整,且呈现规整的正方体形貌;由图3d可见,当反应时间达到8 h时,α-Fe晶粒尺寸分布不均匀,呈现出形状、大小不一的形貌,未观察到具有规整立方体形貌的晶粒.综上所述,当反应温度为120 ℃、反应时间为6.5 h时,可以制备得到规整的立方体状α-Fe.

图3 不同反应时间下α-Fe的SEM图像Fig.3 SEM images of α-Fe at different reaction time
2.3 反应温度对α-Fe形貌的影响
图4为当反应时间为6.5 h时,不同温度下合成样品的SEM图像.由图4a可以观察到,当反应温度为120 ℃时,α-Fe晶粒几乎均为立方体状,且尺寸约为350 nm.由图4b可见,当反应温度继续升高至140 ℃时,α-Fe晶粒的粒径分布开始变得不均匀,呈现出多面体状与部分类球形状.因此,利用溶剂热法合成立方体状α-Fe粉体的最佳反应时间为6.5 h,最佳反应温度为120 ℃.

图4 不同反应温度下α-Fe的SEM图像Fig.4 SEM images of α-Fe at different reaction temperatures
溶剂热反应中乙二胺不仅是反应溶剂,还是α-Fe晶粒的生长模板,能够促使其择优生长.当反应时间达到6.5 h时,各个方向的择优取向相对对称,因而生成了具有立方体形貌的α-Fe.通常情况下,当反应时间较长时,根据奥氏熟化作用可知,小粒子消失不见,晶粒逐渐长大,晶粒的生长对称性遭到破坏,晶粒形状变得无规则.反之,当反应时间较短时,则会引起反应不彻底或产物不纯的后果.不同反应温度会引起α-Fe的结晶速率不同,进而影响晶粒生长形貌.反应温度的选择取决于反应溶质与溶剂,且需要达到临界温度.本文两个反应温度均设定在乙二胺气化临界温度以上,这是因为适当提高反应温度可以增大体系压力,从而有利于改善α-Fe的结晶度.当反应温度为120 ℃时,α-Fe晶粒择优生长,并呈现规整的立方体形貌.但当反应温度升到140 ℃时,由于温度过高,α-Fe活性变强,乙二胺作为α-Fe晶粒的生长模板已不再起作用,此外,反应速率加快,导致α-Fe生长过快,因而失去了立方体形貌.
图5为当反应时间为6.5 h、反应温度为120 ℃时,立方体状α-Fe的TEM图像.由图5可见,当反应时间为6.5 h、反应温度为120 ℃时,所观察到的α-Fe均为正方形,这正是得到的立方体状α-Fe粉体的二维投影.此外,所合成的α-Fe粒径均匀,尺寸均为350 nm,这与SEM研究结果一致.
2.4 α-Fe表面成分分析
图6为立方体状α-Fe的XPS图谱.由图6a可见,α-Fe的XPS图谱中只有O、Fe、C元素,不含有其他杂质元素.α-Fe表面的O元素来自表面层中Fe的氧化物,C元素来自立方体状α-Fe吸附的CO2.为了进一步确定所制α-Fe粉体表面的主要成分,利用XPS高分辨光电子图谱对α-Fe表面进行分析.由图6b可见,结合能707.8与708.9 eV对应单质Fe,而结合能709.9与710.9 eV分别对应Fe2+与Fe3+氧化物.可以确认所合成的立方体状α-Fe粉体是以α-Fe为内核,表面含有少量FeOX的纳米胶囊状结构.

图5 立方体状α-Fe的TEM图像Fig.5 TEM image of cube α-Fe

图6 立方体状α-Fe的XPS图谱Fig.6 XPS spectra of cube α-Fe
2.5 α-Fe吸收剂含量对吸波性能的影响
为了分析所合成样品α-Fe的吸波性能,将α-Fe与石蜡分别按照质量分数20%、30%、40%和50%的比例进行混合.由于石蜡熔点低、易于固形,且只起到粘结作用,因而对吸波性能的影响可以忽略不计.因此,α-Fe晶粒与石蜡混合而成的复合材料的吸波性能可以近似认为就是α-Fe晶粒的吸波性能.利用矢量网络分析仪在室温条件下对样品的复介电常数与复磁导率进行测定.
图7为所合成样品α-Fe的复介电常数与电磁波频率的关系.由图7可见,复介电常数的实部ε′与虚部ε″均随着α-Fe质量分数的增加而增大.当α-Fe的质量分数处于20%、30%、40%、50%范围内时,实部ε′值在低频区随着频率的增加逐渐减少,吸收峰均前移,高频区ε′值变化不大,这是因为立方体状α-Fe内核与表面氧化层的交界面具有较强的电荷传送能力,因而产生了介电弛豫与界面极化现象[9].介电常数虚部ε″分别在3、7、11、15.8 GHz附近出现4个共振峰,这是因为在电磁波作用下,立方体状α-Fe形状各向异性产生的取向极化的增大使得复介电常数也随之增大.其次,立方体状α-Fe形貌为正方体,具有更大的比表面积,因而可能引起更高的空间界面极化.再次,立方体状α-Fe与石蜡混合后,随着α-Fe质量分数的增加,接触面也随之增加,空间界面极化也随之增强.
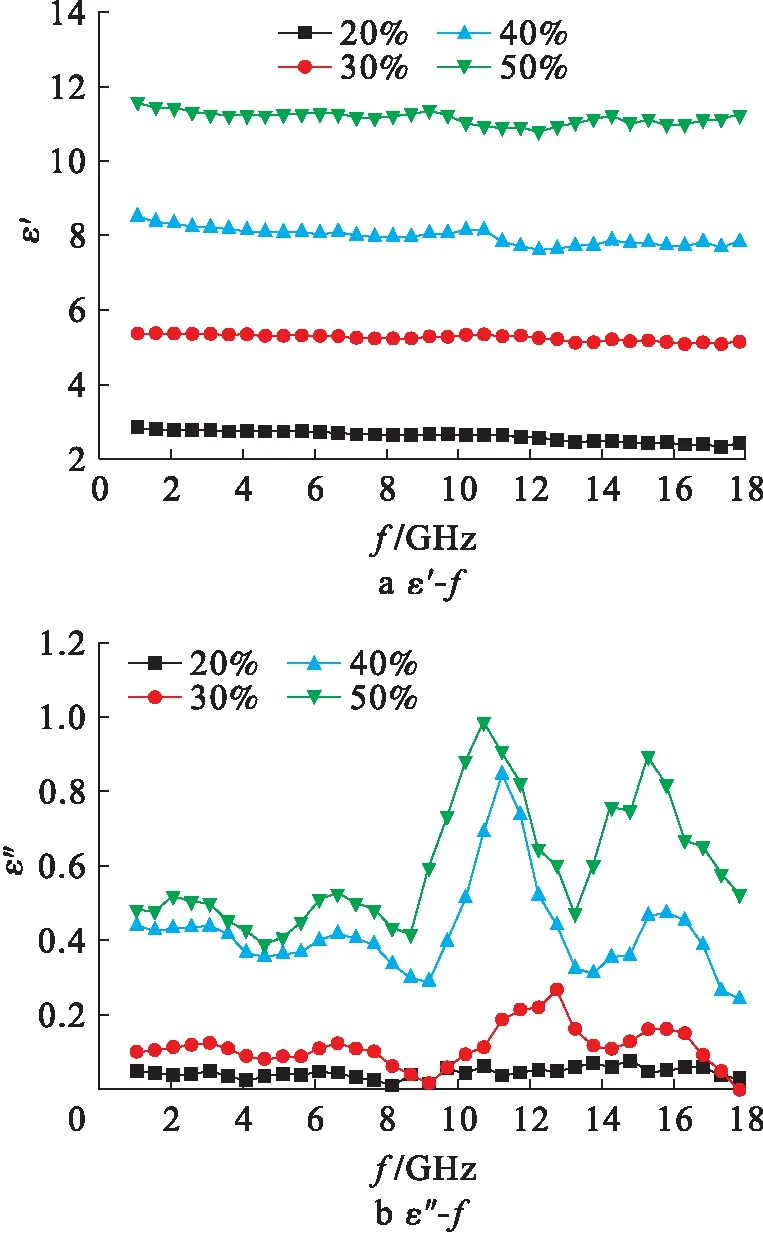
图7 立方体状α-Fe的复介电常数与电磁波频率关系Fig.7 Relationship between complex permittivity and electromagnetic wave frequency of cube α-Fe
图8为所合成样品α-Fe的复磁导率与电磁波频率的关系.由图8可见,复磁导率的实部μ′与虚部μ″均随着α-Fe质量分数的增加而增大,进而影响复合材料的磁性能.当α-Fe的质量分数为20%时,μ′值变化范围为0.97~1.1,而当α-Fe质量分数为30%、40%和50%时,复磁导率实部μ′值变化范围分别为1.08~1.59、1.08~1.84与1.08~2.34.此外,复磁导率实部μ′值在1~9 GHz范围内大幅度下降,而在9~18 GHz范围内趋于平缓.同时,复磁导率的虚部μ″值在1~9 GHz范围内总体上逐渐上升,在9~18 GHz范围内趋于平缓.复磁导率虚部在1~18 GHz范围内出现多个共振峰,各个吸收峰均发生前移.因为立方体状α-Fe具有较大的形状各向异性,与球形磁性纳米铁粉相比,当吸收剂质量分数为50%时,立方体状α-Fe具有更高的自然共振频率,这可能归因于α-Fe的形状各向异性、自然共振和畴壁共振作用,其次也可能是由立方体状α-Fe与石蜡的混合不均匀所致.在9~18 GHz范围内μ′值与μ″值均趋于平缓,这种现象可能是出现了涡流损耗的缘故.
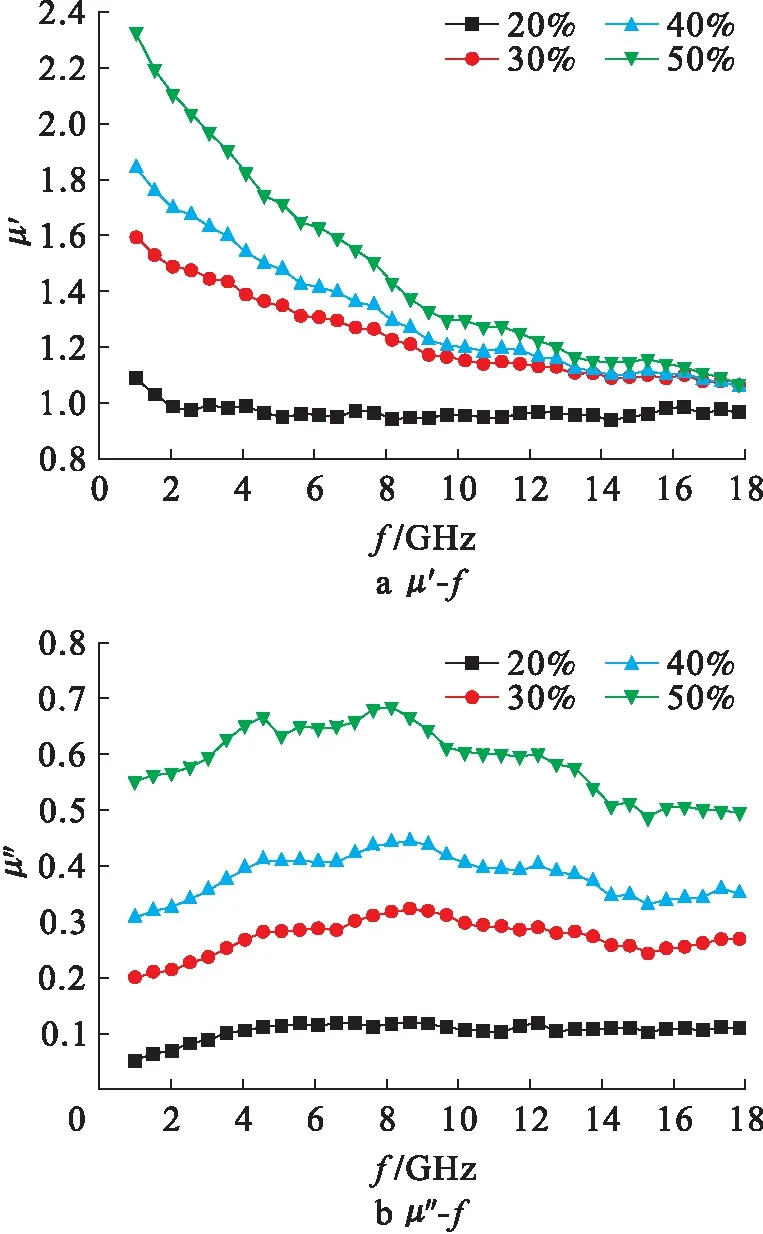
图8 立方体状α-Fe的复磁导率与电磁波频率关系Fig.8 Relationship between complex permeability and electromagnetic wave frequency of cube α-Fe
随着吸收剂质量分数的增大,立方体状α-Fe的介电损耗与磁损耗也随之增大.随着频率的增加,介电损耗变化不大,磁损耗在低频段变化较大.可见,立方体状α-Fe是以磁损耗为主的磁介质型材料,也证明了吸收剂的晶粒形貌与含量是影响介电损耗与磁损耗的两大要素.
为了进一步揭示所合成样品α-Fe的吸波性能,可以根据样品的复介电常数与复磁导率的数值计算模拟得出其反射损耗.图9为立方体状α-Fe的反射损耗RL与电磁波频率的关系.立方体状α-Fe的微波吸收性能如表2所示.由表2可见,当α-Fe质量分数为20%时,不存在反射损耗小于-10 dB的情况.随着吸收剂质量分数的增加,反射损耗小于-10 dB对应的频率范围分别为11.46~18、4.07~18和2.04~18 GHz,对应的涂层厚度范围分别为5.34~7、1.28~5.34和1.28~7 mm.当吸收剂的质量分数分别为30%、40%和50%时,最大反射损耗分别为-24.45、-19.1和-48.9 dB,对应的频率与涂层厚度分别为15.31 GHz和6 mm、10.88 GHz和2 mm以及8.78 GHz和2 mm.结合图9和表2可知,随着吸收剂质量分数的增加,反射损耗小于-10 dB对应的吸收频带变宽,最佳匹配厚度随之减小,进一步表明样品具有较好的电磁匹配.立方体状α-Fe具有较好的形状各向异性,导致其静磁能随之增加.随着吸收剂质量分数的增加,立方体状α-Fe最大反射损耗与对应的涂层厚度、频率呈非线性增强.
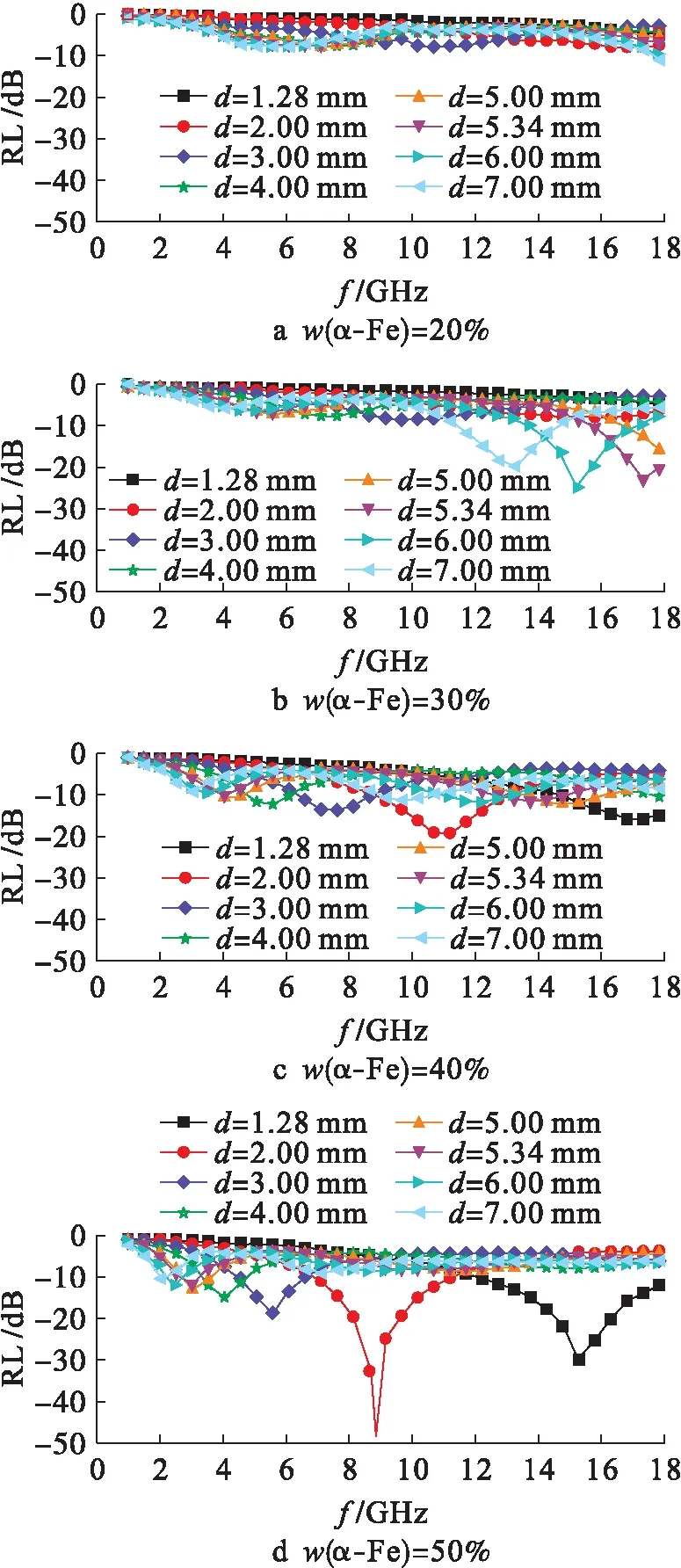
图9 立方体状α-Fe的反射损耗与电磁波频率关系Fig.9 Relationshipbetweenreflectionlossand electromagnetic wave frequency of cube α-Fe
根据传输线理论,判定吸收剂吸收效果的一个关键要素由电磁波衰减系数决定,电磁波衰减系数可以表示为

表2 立方体状α-Fe的微波吸收性能Tab.2 Microware absorption properties of cube α-Fe
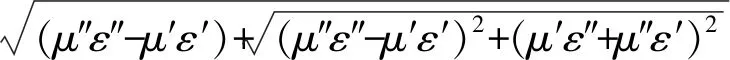
式中,c为光速.
图10为立方体状α-Fe的衰减系数与电磁波频率的关系.由图10可见,随着立方体状α-Fe质量分数的增加,电磁波衰减系数随之增大,阻抗匹配增强,这与图9结果一致.
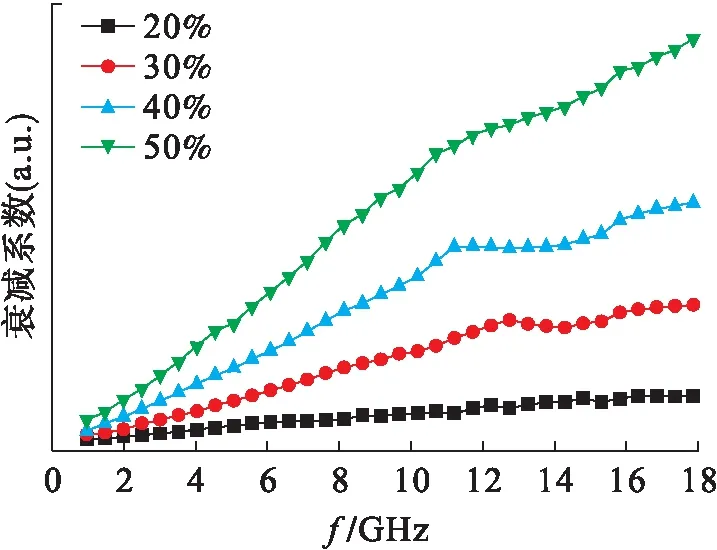
图10 立方体状α-Fe的衰减系数与电磁波频率关系Fig.10 Relationship between attenuation coefficient and electromagnetic wave frequency of cube α-Fe
3 结 论
当反应温度为120 ℃、反应时间为6.5 h时,利用溶剂热法成功合成了具有形状各向异性的立方体状α-Fe.结果表明,在该条件下所合成样品的晶粒尺寸为350 nm.与球状纳米Fe粉相比,立方体状α-Fe的吸波性能得到增强.吸收剂含量的不同引起了复介电常数与复磁导率的改变,进而影响了微波吸收性能.当涂层厚度范围为1.28~7 mm且吸收剂的质量分数分别为30%、40%和50%时,对应的最大反射损耗分别为-24.45、-19.1与-48.9 dB,当RL<-10 dB时,频率范围分别为11.46~18、4.07~18和2.04~18 GHz,对应的涂层厚度范围分别为5.34~7、1.28~5.34和1.28~7 mm.随着吸收剂质量分数的增加,微波吸收特性呈非线性增强.
