基于P-Q解耦变换的智能电网状态估计算法*

徐天福， 罗 庆

(国网江西省电力公司 赣州供电公司， 江西 赣州 341000)

随着我国电力系统电网结构的优化和调整，输电线路电压等级的提高、协调电网的安全稳定运行成为了目前电力系统主要关注的焦点之一[1-3].为了保证电网安全稳定运行，需要对整个电力系统进行精确控制.电力系统能量管理系统EMS结合了计算机技术，可实现电网的信息化调度[4-5].而电力系统状态估计则是EMS技术的基础与核心，其通过状态估计，能够降低量测系统的投资，计算出未测量的电气量，同时，还可以利用两侧系统的冗余信息，提高测量精度[6-7].

目前，配电网系统中广泛使用的是基于最小二乘法或者最小加权值的电力系统状态估计算法[8-10]，例如基于电力系统潮流分析的状态估计算法[11-12]以及考虑电力系统抗差性的功率支路算法[13-14]等.以上算法能够对不同的配电网络进行计算，但由于其计算复杂、时间成本高，难以满足智能电网对状态估计实时处理能力的要求.

基于上述问题，本文提出了一种基于P-Q解耦的，能够有效提高电力系统状态估计计算效率的算法.该算法在对量测量进行变换的同时，能够保留现有的非线性分析，从而完成了雅克比矩阵的稀疏化，且提高了电力系统状态估计的求解速度与准确性.本文以IEEE标准算例验证了该算法的收敛情况及有效性.

1 P-Q解耦变换算法

基于P-Q解耦变化的基本思想是将电力系统的有功功率和无功功率相加，通过补偿电压幅值迭代实现方程的可靠求解[15-17]，解耦迭代方程为

(1)

式中：U为节点电压；θ为相角；ΔP、ΔQ分别为有功功率和无功功率的变化量；J为雅克比矩阵.

传统的P-Q解耦法思路是将有功功率与无功功率相加，从而补偿电导对功率的作用，并讨论对功率和节点电压幅值的影响.通过补偿电压幅值迭代带来的有功功率变化实现功率解耦方程的可靠求解.

本文状态估计算法在P-Q解耦公式的基础上，将量测数据做保留非线性变换，从而进一步简化计算过程、提高状态估计速度.以网络节点电压幅值、相角对其初值的变化量为状态变量，实现状态估计简化求解.

1.1 负荷量测变换

对于节点i，按照P-Q分解法可得其节点功率的表达式为

(Gij+Bij)sinθij]

(2)

式中：Gij、Bij为节点导纳矩阵；θij=θi-θj.

有功功率为

(3)

按照式(1)将节点功率补偿解耦，在实际量测量中减去保留非线性表达式中各个迭代项之后可得

(4)

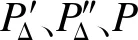
(5)

将非线性变换二项式系数设为初始条件下功率解耦迭代系数，可得节点电压和相角之间的关系矩阵为

(6)

(7)

式中，a∶b表示a可以用表达式b来计算.

1.2 支路功率量测变换

同样将支路功率解耦，对支路功率量测进行非线性变换，可得变换后的量测量为

(8)

(9)

将二次项变换系数作为初始条件下的迭代系数可得

(10)

(11)

式中，Yc为线路对地导纳.

1.3 电压电流量测变换

电压量测值和状态变量之间为线性关系，无需进行变换.电流量测值可以转换为支路的有功与无功功率量，可按照上文所述方法进行对应的量测变换，即

(12)

2 解耦状态估计求解

2.1 状态估计模型

状态估计量测方程表示为

z=h(x)+v

(13)

式中：z为给定的量测矢量；x为待求解的n维状态矢量，h(x)为以状态量x及导纳矩阵建立的量测函数向量；v为量测误差.状态估计的目标函数为

minK(x)=[z-h(x)]TR-1[z-h(x)]

(14)

式中，R为状态估计的协方差矩阵.求解非线性方程极值的必要条件为

(15)

对式(15)的右侧进行数学变换可得

(16)

式中，H为量测雅克比矩阵，化简后可得

HT(x)R-1[z-h(x)]=0

(17)

利用牛顿法对式(17)进行求解可得

f(x)=HT(x)R-1[z-h(x)]=0

(18)

-HT(x)R-1H(x)

(19)

迭代表达式为

Δz(k)=z-h(x(k))

(20)

将迭代形式化简为

Δx(k)=(HTR-1H)-1HTR-1Δz(k)

(21)

x(k+1)=x(k)+Δx(k)

(22)

根据式(6)、(7)、(10)和(11)可知

(23)

同时满足

(24)

因此，经过P-Q解耦变换之后得到的雅克比矩阵为一个稀疏矩阵，即

(25)

化简得

(26)

根据式(26)可得结构变换后的信息矩阵为

(27)

将信息矩阵G代入迭代式(26)求解可得

LTr-1LΔx(U)k+1=LTr-1[zPQ，U-hPQ，U(k)]

(28)

MTr-1MΔx(θ)k+1=MTr-1[zP-hP(k)]

(29)

最后，按照式(22)对方程进行迭代求解，直到满足收敛条件为止.

2.2 计算流程图

本文以初始量测值为状态变量，通过P-Q解耦和保留非线性处理实现了状态估计的快速求解，具体程序流程图如图1所示.

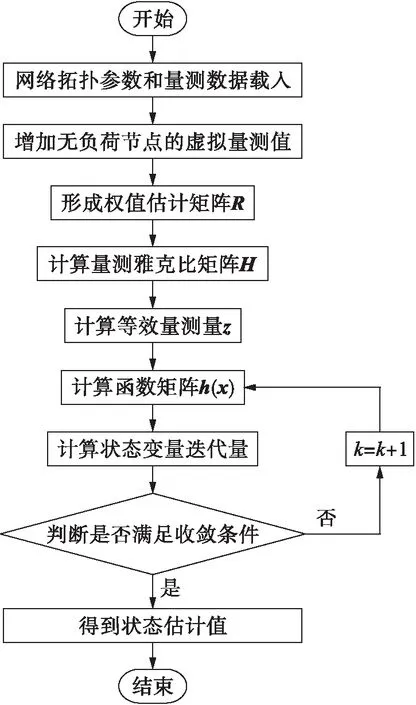
图1 P-Q解耦算法流程图Fig.1 Flow chart of P-Q decoupling algorithm

与传统的WLS算法相比，本文提出的基于P-Q解耦法智能电网状态估计算法计算过程简单，收敛性好，且计算时间成本低，能够适应不同节点网络的计算需求，因此，对于提升电力系统自动化水平具有重要意义.

3 算例分析

本文利用IEEE标准9节点、30节点和57节点系统来证明本算法对不同网络的适用性.算例在MATPOWER工具包中的IEEE标准算例基础上进行，实验过程中量测数据是在潮流分析的基础上，通过迭加正态分布的随机数方法获得，其中，迭加的随机数期望为0，方差为0.02，误差小于1.0×10-4时停止迭代.

本文以平均相对误差计算状态估计结果的正确性，其表达式为

(30)

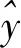
3.1 IEEE标准9节点网络

图2为IEEE标准9节点网络拓扑图，其中，G代表发电机节点，数字为母线编号，节点5，6，8为负荷节点，由黑色箭头标记.电压计算结果如图3所示，节点电压状态估计值平均相对误差为9.47×10-6，计算时间约为0.04 s.

图2 IEEE标准9节点网络拓扑图Fig.2 IEEE standard 9-node network topology

图3 9节点网络电压计算结果Fig.3 Computing results of voltage in 9-node network

由状态估计计算结果可知，系统总有功功率为320 MW，无功功率为34.9 MVar；复合消耗的总有功功率为315 MW，无功功率为115.0 MVar；线路损耗有功功率4.95 MW，无功功率51.31 MVar.表1为网络主要参数计算结果.

表1 9节点网络主要参数计算结果Tab.1 Computing results of main parameters for 9-node network

3.2 IEEE标准30节点网络

图4为IEEE标准30节点网络拓扑图.其中，包含发电机节点6个，负荷节点21个.节点电压计算结果如图5所示.节点电压状态估计值平均相对误差为7.467×10-5，计算时间约为0.03 s.

图4 IEEE标准30节点网络拓扑图Fig.4 IEEE standard 30-node network topology

图5 30节点网络电压计算结果Fig.5 Computing results of voltage in 30-node network

由状态估计计算结果可知，系统总有功功率为192.5 MW，无功功率为99.3 MVar；复合消耗总有功功率为191.1 MW，无功功率为106.4 MVar；线路损耗有功功率2.32 MW，无功功率9.01 MVar.表2为网络主要参数计算结果.

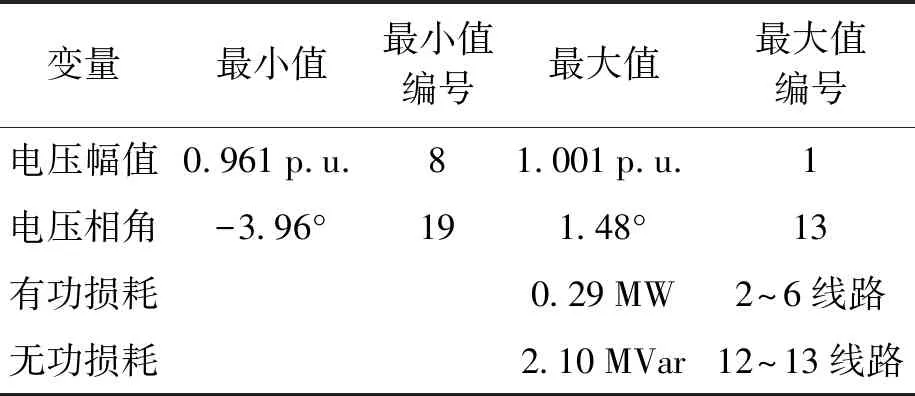
表2 30节点网络主要参数计算结果Tab.2 Computing results of main parameters for 30-node network

3.3 IEEE标准57节点网络

图6为IEEE标准57节点系统网络拓扑图，该系统包含7个发电机节点，42个负荷节点，变压器节点17个.节点电压计算结果如图7所示，其中，平均相对误差为0.001 7，计算时间约为0.13 s.

图6 IEEE标准57节点网络拓扑图Fig.6 IEEE standard 57-node network topology

由状态估计计算结果可知，系统总有功功率为128.87 MW，无功功率为312.2 MVar；负荷消耗的总有功功率为114.07 MW，无功功率为310.2 MVar；线路损耗有功功率26.68 MW，无功功率112.76 MVar.表3为网络主要参数计算结果.

图7 57节点网络电压计算结果Fig.7 Computing results of voltage in 57-node network

变量最小值最小值编号最大值最大值编号电压幅值0.936p.u.311.601p.u.46电压相角-19.38°312.0°1有功损耗3.9MW1～15线路无功损耗19.96MVar1～15线路

4 结 论

本文分析了电力系统状态估计中的P-Q解耦算法，以量测值为初始变量，在解耦过程中保留了非线性变换，使雅克比矩阵稀疏化、常数化，算法求解过程简单，实现了状态估计的快速求解.

以不同的IEEE标准算例为实验对象，通过迭加正态分布随机数的方法获得量测数据，验证了计算模型的准确性和适用性.这对于提高电力系统自动化水平具有一定积极作用.