非淹没异侧双体丁坝水流恢复区长度计算

潘 海 静，顾 正 华，李 云，张 荣 茂

(1.浙江大学 建筑工程学院，浙江 杭州 310058； 2.南京水利科学研究院，江苏 南京 210029； 3.浙江大学 数学科学学院，浙江 杭州 310027)

1 研究背景

丁坝是一种广泛应用于河流海岸工程的涉水建筑物，可用于改变流向，减小岸边流速，防止河岸(床)遭受侵蚀[1-3]；维持合适的水深与河宽，保障航道尺度[4]；改变局部冲淤，形成河滩堆积物，构造新河岸[1]；防止河口和海岸被波浪侵蚀[1，5]；改善河道生境条件等[1]。在我国的长江[1，4]、黄河[4]、钱塘江[6]以及国外莱茵河[1，7]、密西西比河等治理工程中都有应用[1，4，7]。实际工程中按照丁坝布置的数量，可分为单体丁坝和丁坝群[1-2]，而单体丁坝很难发挥充分的作用，通常是由丁坝群产生的累积效应来发挥作用[8]。前人对丁坝水流结构的定量研究主要关注的是回流区，而较少有人研究丁坝的恢复区，这是因为恢复区位于回流末端断面的下游[5]，实际测量比较困难，导致目前还没有这方面的计算依据。但它作为河流系统丁坝群布置的一个重要指标，对实际治河工程具有重要指导作用，为此，本文开展了非淹没异侧双体丁坝恢复区长度的计算研究。

2 材 料

2.1 恢复区长度的计算方法

基于大尺度涡不相重叠的作用尺度划分准则(准则Ⅰ)[2]中涉及到的回流区长度计算相关的研究较多，所获得的结果较成熟，更具一定的参考价值。而基于下游丁坝断面流速分布恢复的作用尺度划分准则(准则Ⅲ)[2]与基于双丁坝断面流速分布相似的作用尺度划分准则(准则Ⅱ)[2]的判断标准本质相同，两者的结果也很接近，相比之下，准则Ⅲ实际操作更复杂。本文在综合比较下采用准则Ⅰ和准则Ⅱ开展恢复区长度的计算。

结合图1的分析可以看出，准则Ⅰ获得的流场分布中恢复区长度恰好为0，准则Ⅱ获得的间距阈值(S2)等于恢复区长度(S)与准则Ⅰ之下的间距阈值(S1)之和，进一步推导出S可以转化为S2与S1之差。

图1 恢复区长度计算示意Fig.1 Schematic diagram of the length of recovery area calculation

2.2 数据收集

2.2.1 模型的建立

本文的数值模拟部分采用计算流体力学(CFD)商用软件FLUENT进行分析。湍流模型选择中，RNG κ-ε紊流模型在分离流和曲线流以及弱漩涡中具有更好的性能[9]，为此本文选择该模型进行研究；网格采用六面体结构化网格，计算中选择压强基求解器；模型求解时，压强与速度的耦合采用SIMPLEC算法，动量、紊动能和紊动能耗散率的差分格式采用一阶迎风；在边界条件设置时，入口来流采用velocity-in，水槽的竖直面和底面以及丁坝坝体都视为固壁并且满足无滑移条件，非淹没双体丁坝自由表面采用刚盖假定，出口断面采用outflow。

2.2.2 模型验证

采用水槽试验进行数学模型的验证，水槽试验中的丁坝和测量断面布置如图2所示。定义沿水槽主流方向为X轴，沿水深方向为Y轴，沿丁坝轴线方向为Z轴；丁坝A0、A的长度为0.4 m，B0、B的长度为0.3 m，C0、C的长度为0.2 m，D0、D的长度为0.1 m，流量Q=0.065 9 m3/s，水深h=0.3 m，同时选取每两个丁坝中间的断面b4、z3、z9、x8、d8、d16、d22和下游断面d0作为验证断面。图3给出了水平面Y=0.24 m上不同验证断面流速u的模拟结果与实测结果沿Z轴方向的对比分布。

图2 水槽试验示意Fig.2 Schematic diagram of flume experiment

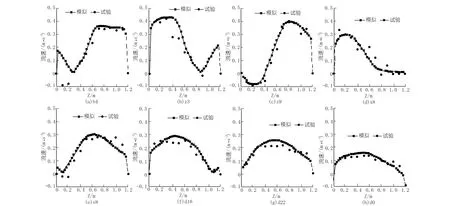
图3 不同验证断面上流速计算值与实测值对比 Fig.3 Comparison between the calclated and measured velocity on different verification secrions

由图3可以看出， 数值模拟结果与水槽试验的测量结果吻合度较高，两者的分布趋势基本一致，说明RNG κ-ε紊流模型可以作为丁坝水流模拟研究的工具。

2.2.3 数值试验工况

根据非淹没双体丁坝的无量纲表达式(1)和(2)[10]，本文仍采用文献[10]的数值模拟试验工况，见表1。

(1)

(2)

3 结果分析

3.1 基于大尺度涡不相重叠的间距阈值计算

借鉴同侧双体丁坝[2]，基于准则I的异侧双体丁坝间距阈值应该定义为上游丁坝下游回流区与下游丁坝上游回流区刚好在同一水槽横截面处不重叠时两丁坝的间距，即为划分大小尺度丁坝群的临界值。

在表1的试验工况下，通过不断地加大丁坝2与丁坝1之间的距离来研究顺直棱形河道中异侧布置的非淹没双体丁坝相对间距阈值随各影响因素的变化规律，依次得到Sc/b与Fr、B/h、B/b之间的关系，如图4所示。

由图4可以看出，当B/h和B/b保持不变时，Sc/b随着Fr的增大先减小后增大，Sc/b的最小值出现在Fr=0.3附近，Sc/b和Fr之间的关系是一个带有向上开口的二次函数；接着固定Sc/b和B/h，Sc/b随着B/h增加单调减小，当B/b小于6时，Sc/b的下降速度非常快，然后变得比较平缓，Sc/b与B/b之间满足幂函数关系；最后将Fr和B/b保持不变研究Fr与B/h之间的关系，发现Sc/b随着B/h增加单调增加，Sc/b的增长速率先大后小，Sc/b与B/h之间大概呈现对数函数关系。

表1 非淹没丁坝群数值模拟试验工况

Tab.1 Numerical simulation test conditions of non-submerged spur dikes

编号B/mb/mh/mQ/(m3·s-1 )FrB/hB/bc11.20.20.20.03360.166c21.20.20.20.06720.266c31.20.20.20.10080.366c41.20.20.20.16800.566c51.20.20.20.23520.766c61.20.50.20.06720.262.4c71.20.40.20.06720.263c81.20.30.20.06720.264c91.20.20.20.06720.266c101.20.10.20.06720.2612c110.60.10.30.06180.226c121.20.20.30.12350.246c131.20.20.20.06720.266c141.80.30.20.10090.296c152.40.40.20.13450.2126

注：工况c2，c9和c13相同。

对图4中的3组数据进行多元回归分析，得到准则Ⅰ下的非淹没异侧双体丁坝间距阈值的经验公式见式(3)。将经验公式(3)的计算结果与CFD数值模拟的结果进行比较。由图5可以看出，公式(3)的计算结果与数学模型的计算结果吻合较好，计算精度令人满意。

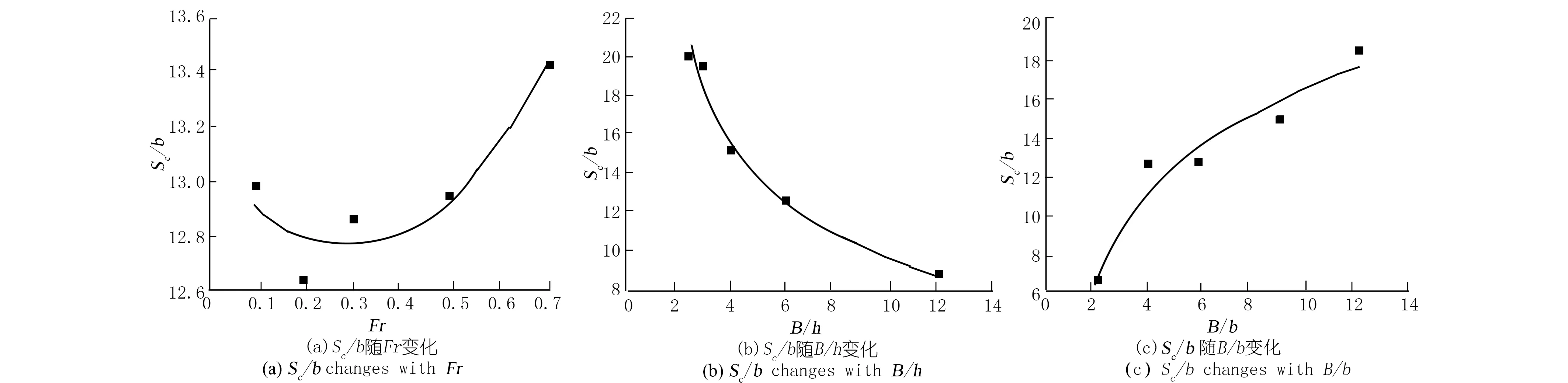
图4 Sc/b随Fr、B/h、B/b的变化Fig.4 Sc/bchanges withFr、B/h、B/b

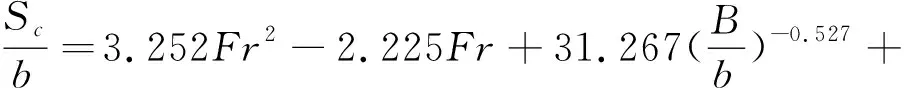
(3)

3.2 恢复区长度计算

公式(4)为准则Ⅱ的间距阈值经验公式[10]。由前面的恢复区长度理论分析可知，将公式(4)与公式(3)相减，即得到非淹没异侧双体丁坝恢复区长度S的计算公式，如式(5)所示。

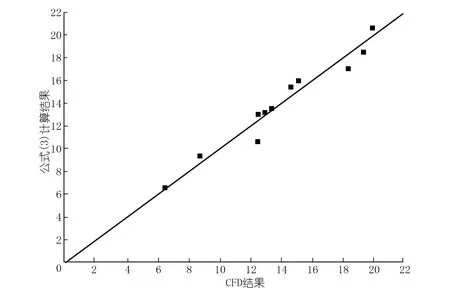
图5 经验公式(3)的计算效果检验Fig.5 Calculation effect test of empirical formula

(4)

(5)

3.3 公式检验

采用如表2所列的4种检验工况进行数值模拟，将模拟得到的恢复区长度与公式(5)的计算值进行比较，结果见表3。可以看出，两者之间的差值很小，误差均可控制在10%之内，说明本文所建立的非淹没异侧双体丁坝恢复区长度计算经验公式具有较好的计算精度，可供河流系统丁坝群作用尺度分析使用。

表2 恢复区长度计算公式的检验工况

Tab.2 Test conditions of formula for calclation of length of recovery zone

编号B/mb/mh/mQ/(m3·s-1 )FrB/bB/hy11.00.200.250.15660.4054y21.50.150.200.10510.25107.5y33.00.750.200.75640.90415y43.00.200.300.12350.081510

表3 CFD和经验公式(5)计算结果对比

Tab.3 Comparison of calculation results between CFD and Empirical formula(5)

编号CFD计算值/m公式(5)计算值/m相对误差/%y111.31711.880-4.97y210.98210.7342.26y39.3548.4929.22y444.52646.481-4.39

4 结 语

根据水槽试验资料，采用RNG紊流模型建立了丁坝水流模拟的数学模型。将恢复区长度转化为基于双丁坝断面流速分布相似划分准则(准则Ⅱ)下的间距阈值与基于大尺度涡不相重叠的作用尺度划分准则(准则Ⅰ)下的间距阈值之差。通过数值模拟试验得到非淹没异侧双体丁坝基于准则Ⅰ下的间距阈值经验公式。在此基础上，获得非淹没异侧双体丁坝恢复区长度计算经验公式，计算结果的检验效果令人满意，可供河流系统丁坝群作用尺度分析和丁坝群合理布置参考。