基于改进粒子群算法的机器人几何参数标定研究
2019-05-30温秀兰吕仲艳贺顺王东霞康传帅赵艺兵
温秀兰 吕仲艳 贺顺 王东霞 康传帅 赵艺兵


摘要 为了提高机器人末端绝对定位精度,提出了基于改进粒子群算法(IPSO)的机器人几何参数标定方法.首先,为避免当机器人相邻两轴线平行或接近平行时,模型存在奇异性,建立了串联机器人MDH模型;其次,针对机器人几何参数标定特点,提出用改进粒子群算法优化标定机器人几何参数,其中粒子初始位置和速度由拟随机Halton序列产生,采用浓缩因子法修改粒子飞行速度,建立了用IPSO标定机器人几何参数目标函数数学模型,确立了用该算法优化标定几何参数的具体步骤.通过对ER10L-C10工业机器人仿真与实测标定,结果证实:采用该方法能够快速标定机器人几何参数,经标定后的机器人末端绝对定位精度有大幅提高.该算法简单,鲁棒性强,易于在工业机器人标定中推广应用.
关键词 机器人;几何参数标定;改进粒子群算法;绝对定位精度
中图分类号 TP391;TB92
文献标志码 A
0 引言
高端制造业的持续发展提高了对工业机器人的精度要求,尤其是在激光焊接、激光切割以及航空航天等应用领域.工业机器人定位性能的衡量指标主要有重复定位精度和绝对定位精度[1].目前工业机器人的重复定位精度可达到0.02~0.1 mm,而绝对定位精度仅为毫米级.传统的机器人在制造业中主要担任着一些重复性的简单工作,而且多采用示教再现的模式.这类工作的特点是仅需要机器人多次重复到达同一位置,因此机器人的高重复定位精度起了很大作用[2-3].随着机器人在航空航天、柔性制造等领域应用日渐广泛,对机器人系统的高精度控制提出了更严格的要求,与其现有的绝对定位精度及定位稳定性之间存在突出的矛盾.機器人标定能够较好地提高机器人的绝对定位精度[4-5].机器人标定分为关节级标定、几何参数(即运动学)标定与非几何参数(非运动学)标定.由于机械加工误差、装配误差、磨损等因素影响,使得工业机器人实际参数和理论设计参数存在着偏差,导致其工作性能降低,而且由于结构特征、安装位姿等要素的影响,现场直接测量获得的机器人结构参数往往不够准确,直接导致了末端位姿精度的降低[6].研究发现,机器人几何参数误差是影响机器人作业精度的主要误差源,约占总误差的90%,通过对机器人几何参数的标定,可以有效提高机器人定位精度[7].因此机器人几何参数标定问题是机器人高精度定位控制的基础和核心问题,也是机器人领域的难点问题[8].
机器人几何参数标定通常分为建模、测量、辨识和补偿4步.其中,DH模型是常用的几何参数模型之一,该模型通过齐次变换矩阵来描述相邻连杆之间的空间关系.但是,当机器人相邻关节旋转轴线平行或接近平行及垂直或接近垂直时出现奇异点,无法满足模型连续性的要求,直接影响标定结果的准确性.为了解决该问题,在传统的DH模型基础上Hayati提出了改进的DH模型(MDH模型)[9],通过增加一个旋转参数,弥补了DH模型的缺陷,解决了相邻关节旋转轴线平行或接近平行时出现奇异点的问题[10].辨识是从测量数据中获取机器人实际模型参数信息的过程,其辨识的结果对机器人绝对定位精度的提高有直接影响.传统的辨识方法有最小二乘法、LM 方法、卡尔曼滤波法等.考虑到几何参数标定属于复杂的非线性优化问题,智能计算在解决复杂优化问题时有独到之处,因此,近年来已有学者尝试将遗传算法、粒子群优化算法等智能计算应用于对机器人参数辨识并取得了一定效果[11-14].其中:文献[11]建立了六自由度机器人的MDH模型,通过计算种群的适应值按照赌轮法选择个体,根据事先设定的概率进行交叉和变异操作,通过仿真证实了算法的有效性;文献[12]提出了基于改进遗传算法的空间机器人动力学参数辨识研究;文献[13]提出通过采用扩展卡尔曼滤波和神经网络算法提高机器人标定精度;文献[14]利用闭环矢量链法和DH矩阵法分别建立并联机器人和串联机器人的运动学误差模型,采用量子粒子群优化算法对五轴并联机床几何参数进行实验标定.总结现有研究结果发现,目前将智能计算用于机器人几何参数标定,多是通过仿真结果验证算法的有效性.本文建立了串联机器人MDH模型,提出将基于拟随机序列产生初始位置和浓缩因子法修改粒子速度的改进粒子群算法用于机器人几何参数标定,通过仿真实验和实测机器人来提高机器人绝对位置精度.
1 机器人几何参数标定的数学模型
1.1 MDH模型建立
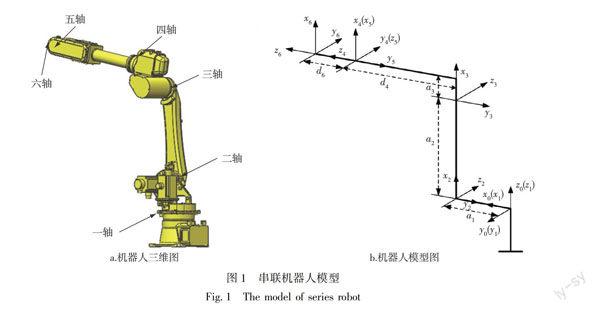
机器人常用模型为DH模型,该模型当机器人相邻两轴平行或接近平行时存在奇异性,为解决该问题,本文建立图1所示串联机器人MDH模型.
依据MDH模型可以得到机器人连杆相邻坐标系之间的变换关系[15],即:
式中ai,di,αi,θi,βi分别表示机器人第i个关节的连杆长度、连杆偏距、关节扭角、关节角及关节扭角的名义值,i=1,2,…,n,n为关节数目,s和c分别表示sin和cos的缩写.机器人末端的名义位姿可由名义位姿矩阵Tn求取:
式(2)中,Rn∈R3×3和Pn∈R3×1分别为名义姿态旋转和位置平移矩阵.由式(1)和(2)可见,机器人末端位姿是机器人几何参数ai,di,αi,βi及关节角θi的函数.当几何参数ai,di,αi,βi,θi存在误差Δai,Δdi,Δαi,Δβi,Δθi时,机器人末端实际位姿可由实际转换矩阵Tr计算:
根据机器人微分运动学原理,机器人末端的位姿变化矩阵dT可以用相对于基坐标系的微分变换矩阵μ以及名义位姿矩阵Tn表示为
其中微分变换矩阵μ可表示为
式(5)中d=(dx,dy,dz)T代表一阶微分平移向量,δr代表一阶微分旋转矩阵,其中Δδ=(δx,δy,δz)T表示机器人末端实际姿态相对于名义姿态的误差.
将式(2)、(5)代入式(4)得:
式中Δp=(δpx,δpy,δpz)T代表机器人末端实际位置相对名义位置的误差.
1.2 目标函数
采用改进粒子群算法搜索优化机器人几何参数误差时,其目标函数定义为
式(7)中N为标定点数目,k为调节因子.由式 (1)—(7)可见,f是几何参数误差集(Δai,Δdi,Δαi,Δβi,Δθi)的函数,机器人几何参数标定实质是通过设定机器人在不同组关节角(θ1j,θ2j,θ3j,θ4j,θ5j,θ6j)下获得其末端位置和姿态的实际值与名义值的误差,通过优化搜索机器人几何参数误差集(Δai,Δdi,Δαi,Δβi,Δθi),使目标函数f为最小.例如图1所示待标定的六自由度串联机器人,因第 2、3 轴线在理论上是互相平行的,参数d2,β1,β3,β4,β5,β6不需要辨识,因此待优化的几何参数误差为
Δa1,Δa2,Δa3,Δa4,Δa5,Δa6,Δd1,Δd3,Δd4,Δd5,Δd6,Δα1,Δα2,Δα3,Δα4,Δα5,Δα6,Δβ2,Δθ1,Δθ2,Δθ3,Δθ4,Δθ5,Δθ6,共24個参数,属于复杂约束的非线性优化问题,非常适宜于用粒子群算法求解.
2 改进粒子群算法用于几何参数标定
粒子群算法是由J.Kennedy和R.C.Eberhart提出的一种新的智能算法.其优化机理也是从随机解出发,根据适应度或目标函数来评价解的品质,通过追随当前搜索到的最优值来寻找全局最优解.该算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,在移动机器人路径规划、基于网络的数据分类、Lévy 噪声数据拟合等实际工程问题中得到成功应用[16-18].
2.1 拟随机Halton序列
考虑到传统粒子群算法中粒子的初始位置采用伪随机数随机产生,而伪随机数序列随机性过强而均匀性不足,比伪随机数序列更加均匀地充满采样空间的序列是拟随机数,可以加快收敛速度.本文采用拟随机Halton序列在区间[0,1]上产生参数值ti(i=1,2,…,M),M通常取足够大的值使ti均匀地充满采样空间[0,1],表示如下:
Halton序列中的第k个元素由式(9)求得.
2.2 基于IPSO的机器人几何参数标定
用IPSO标定机器人几何参数误差时,粒子的速度由下述浓缩因子法修改:
vt+1i=K(vti+C1r1(ptbest,i-pti)+C2r2(gtbest-pti)),
其中φ=c1+c2,φ>4,vti 和pti 分别为第i个粒子在第t代的速度和位置,r1 、r2为[0,1]之间均匀分布随机数,c1、c2 为加速系数,决定了第i个粒子飞向局部最优个体ptbest,i 和全局最优个体gtbest的能力,粒子的收敛速度由φ控制.
采用IPSO标定机器人几何参数步骤如下:
步骤1.设置算法初始化控制参数.
步骤2.输入被标定机器人几何参数的名义值.
步骤3.生成粒子的初始位置和初始速度.
采用拟随机Halton序列产生两组psize×N维的实数向量作为粒子的初始位置pti 和初始速度vti,i=1,2,…,psize,psize为种群规模,N为待优化变量的个数;t=1时设定粒子i的初始位置为其最优位置ptbest,i,选取初始粒子中目标函数值最小的粒子的位置作为初始全局最佳粒子位置gtbest.
步骤4.根据机器人所有标定点关节角、实测位姿及名义位姿计算粒子的目标函数值f(pti),目标函数值越小,粒子越趋于最优解..
步骤5.采用式(10)浓缩因子法修改粒子速度vt+1i.
步骤6.根据修改后的粒子速度改变粒子位置pt+1i.
pt+1i=pti+vt+1i Δt,
其中Δt 是时间步长,设置为1,
步骤7.计算粒子位置改变后的所有粒子目标函数值f(pt+1i).
步骤8.更新局部最佳粒子位置ptbest,i.
步骤9.更新全局最佳粒子位置gtbest.
步骤10.判断是否满足终止条件,若不满足,则t=t+1转步骤5.终止条件设定为算法的最大进化代数.
步骤11.输出被标定机器人几何参数值,并计算标定前后机器人末端位置和方向误差.
3 实验与结果
3.1 仿真实验
3.1.1 位姿产生
为了验证算法的有效性,从ER10L-C10工业机器人手册中获取该机器人DH模型几何参数见表1.分别在[-0.01,0.01](单位:rad)和[-0.05,0.05](单位:mm)区间范围内随机均匀产生几何参数误差如表2所示,几何参数实际值根据表1理论值和表2设定的误差获得.〖KH+1D〗表1 ER10L-C10机器人名义参数
在[-π,π](单位:rad)区间内按照均匀分布随机产生32组理论关节角θ1j,θ2j,θ3j,θ4j,θ5j,θ6j,j=1,2,…,32.考虑到机器人因加工、装配、磨损等误差会导致由机器人示教器设定的关节角与实际关节角间有误差存在,实际关节角为在理论关节角上加入[-0.1,0.1](单位:rad)服从均匀分布的随机噪声.将关节角及几何参数的理论值和实际值分别代入式(2)—(6),即可求出机器人末端位置和方向的理论值与实际值及位置和方向误差.
3.1.2 仿真实验结果
根据上述随机生成的几何参数误差和关节角,采用IPSO优化求解机器人几何参数,算法的控制参数设定为:粒子种群规模psize为20、加速系数c1、c2均为2.05、最大进化代数为2 000.初始种群中角度和长度几何参数误差分别在±0.01 rad和±0.5 mm区间范围内采用拟随机Halton序列产生.图2为IPSO在Intel(R) Core(TM) i5-4570 CPU主频3.20 GHz计算机上采用Matlab10.0优化搜索机器人的几何参数过程,完成2 000代进化所需时间分别为220 s.图3绘制了机器人末端绝对位置误差在标定前及经IPSO标定后的比较结果,图4和图5分别给出了机器人末端在标定前后绕X轴、Y轴和Z轴旋转的方向误差,由仿真实验结果可见:提出的ICSA不仅能够快速完成机器人几何参数标定,而且标定后的位置和方向误差均小于标定前,特别是绝对位置精度大幅提高.
3.2 實测结果
采用提出方法对埃夫特ER10L-C10工业机器人进行标定实验,为了能够同时测量机器人末端位置和方向,采用Leica AT960激光跟踪仪,TMAC安装在机器人末端的法兰上,测量环境如图6所示.实验时用跟踪仪提供的RoboDyn软件随机产生30个位姿点,对应生成30组关节角进行机器人标定实验.
为了减小测量误差影响,在设定的每组关节角下对末端位姿重复测量10次,取其平均值作为实际测量值.采用提出的IPSO对该机器人几何参数进行标定,标定前后机器人绝对位置误差和X轴、Y轴和Z轴绝对方向误差计算结果如表3所示.其中机器人末端绝对位置误差的平均值、标准差和最大值由标定前的9.679 4、5.223 0和12.078 1 mm减小为标定后的1.778 5、0.482 0和4.643 3 mm.图7给出了机器人末端绝对位置误差在标定前后的比较结果,图8和图9分别给出了机器人末端X轴、Y轴和Z轴在标定前后的方向误差,可见,采用提出的ICSA对机器人几何参数标定后其绝对位置精度大幅提高,在不改变硬件设备情况下能够使机器人绝对定位精度明显提升.
4 结束语
本文根据高端制造业对工业机器人高精度的要求,提出了基于改进粒子群算法的机器人几何参数标定方法,针对当机器人相邻两轴线平行及接近平行时模型存在的奇异性问题,建立了机器人MDH模型,给出了用该算法优化求解几何参数误差的具体步骤.仿真实验及实测结果证实采用提出方法能够快速完成机器人几何参数标定,经标定的机器人末端绝对位置精度会大幅提高,适于在有高精度位置要求的串联机器人几何参数标定中推广应用.
参考文献
References
[1] Greenway B.Robot accuracy[J].Industrial Robot:an International Journal,2000,27(4):257-265
[2] Joubair A,Bonev I A.Kinematic calibration of a six-axis serial robot using distance and sphere constraints[J].The International Journal of Advanced Manufacturing Technology,2015,77(1/2/3/4):515-523
[3] 杨聚庆,王大勇,董登峰,等.激光测量标定机器人坐标系位姿变换的正交化解算[J].光学精密工程,2018,26(8):1985-1993
YANG Juqing,WANG Dayong,DONG Dengfeng,et al.Laser measurement based evaluation for orthogonal transformation calibration of robot pose[J].Optics and Precision Engineering,2018,26(8):1985-1993
[4] 白云飞,丛明,杨小磊,等,基于6参数模型的 6R 串联机器人运动学参数辨识[J].机器人,2015,37(4):486-492
BAI Yunfei,CONG Ming,YANG Xxiaolei,et al.Kinematic parameter identification for 6R serial robots based on a 6-Parameter model[J].Robot,2015,37(4):486-492
[5] 李睿,曲兴华.工业机器人运动学参数标定误差不确定度研究[J].仪器仪表学报,2014,35(10):2192-2199
LI Rui,QU xinghua.Study on calibration uncertainty of industrial robot kinematic parameters[J].Chinese Journal of Scientific Instrument,2014,35(10):2192-2199
[6] Guo Y,Yin S B,Ren Y J,et al.A multilevel calibration technique for an industrial robot with parallelogram mechanism[J].Precision Engineering,2015,40:261-272
[7] Chen G,Li T,Chu M,et al,Review on kinematics calibration technology of serial robots[J].International Journal of Precision Engineering and Manufacture,2014,15(8):1759-1774
[8] GB/T 12642—2013工业机器人:性能规范及其试验方法[S].2013
GB/T 12642-2013 Industial robots:performance criteria and related test methods[S].2013
[9] Hayati S A.Robot arm geometric link parameter estimation[C]∥The 22nd IEEE Conference on Decision and Control.San Antonio,USA,1983:1477-1483
[10] Kazerounian K,Qian G Z.Kinematic calibration of robotic manipulators[J].Journal of Mechanisms Transmissions and Automation in Design,1989,111(4):482
[11] Liu Y.Calibration of a 6-DOF space robot using genetic algorithm[J].Chinese Journal of Mechanical Engineering (English Edition),2008,21(6):6
[12] 劉宇,李瑰贤,夏丹,等.基于改进遗传算法辨识空间机器人动力学参数[J].哈尔滨工业大学学报,2010,42(11):1734-1739
LIU Yu,LI Guixian,XIA Dan,et al.Identifying dynamic parameters of a space robot based on improved genetic algorithm[J].Journal of Harbin Institute of Technology,2010,42(11):1734-1739
[13] Nguyen H N,Zhou J,Kang H J.A calibration method for enhancing robot accuracy through integration of an extended Kalman filter algorithm and an artificial neural network[J].Neurocomputing,2015,151:996-1005
[14] 房立金,党鹏飞,基于量子粒子群优化算法的机器人运动学标定方法[J].机械工程学报,2016,52(7):23-30
FANG Lijin,DANG Pengfei.Kinematic calibration method of robots based on quantum-behaved particle swarm optimization[J].Journal of Mechanical Engineering,2016,52(7):23-30
[15] Nguyen H N,Zhou J,Kang H J.A new full pose measurement method for robot calibration[J].Sensors,2013,13(7):9132-9147
[16] Dewang H S,Mohanty P K,Kundu S.A robust path planning for mobile robot using smart particle swarm optimization[J].Procedia Computer Science,2018,133:290-297
[17] Carneiro M G,Cheng R,Zhao L,et al.Particle swarm optimization for network-based data classification[J].Neural Networks,2019,110:243-255
[18] Marouani H,Fouad Y.Particle swarm optimization performance for fitting of Lévy noise data[J].Physica A:Statistical Mechanics and its Applications,2019,514:708-714
Study on robot geometric parameters calibration based on
improved particle swarm algorithm
WEN Xiulan1 LU Zhongyan1 HE Shun1 WANG Dongxia1 KANG Chuanshuai1 ZHAO Yibing1
1 Automation Department,Nanjing Institute of Technology,Nanjing 211167
AbstractIn order to improve the absolute positioning accuracy of a robot end-effector,a calibration method based on an improved particle swarm algorithm (IPSO) is proposed.Firstly,in order to avoid singularity in the model when two adjacent axes of the robot are parallel or close to parallel,the MDH model of series robot is founded.Secondly,according to the calibration features of robot geometric parameters,IPSO is used to optimize and calibrate the robot geometric parameters.The initial positions are generated based on Halton sequences and the particle velocity is modified by the constriction factor approach.The mathematical model of the objective function to calibrate robot geometric parameters based on IPSO is established,and detailed steps are provided for using IPSO to optimize geometric parameters.The results of the simulation and real calibration of the ER10L-C10 industrial robot show that the proposed method can quickly calibrate the geometric parameters of the robot,and the absolute positioning accuracy of the end-effector is greatly improved.The proposed algorithm is simple and robust,and is suitable to be popularized and applied in industry robot calibration.
Key wordsrobot;geometric parameters;improved particle swarm algorithm;absolute positioning accuracy
