电推进在电磁编队飞行碰撞规避控制中的应用
2019-05-30白敬王婷
白敬 王婷


摘要 由于地球磁场的影响,电磁编队可以在近地轨道稳定飞行,通过改变电磁卫星磁极的电流大小来保持一定的编队队形.虽然地球磁场通常被看作偶极场,并随地球旋转,但地球磁场与电磁力场之间的相互作用被认为是一种内力.当电磁卫星编队突然遇到障碍物需要积极避障时,电磁力作为内力不能改变编队方向,因此,必须对电磁卫星编队施加外力,以实现碰撞规避控制.本文研究了电推进技术在电磁卫星编队碰撞规避中的应用.在此过程中,电推进提供编队转向所需的外部推力,而電磁力作为辅助推力共同作用实现碰撞规避.电推进采用多模态霍尔推力器,基于模糊推断的LQR重构控制方法进行碰撞规避过程的控制,并通过数字仿真验证了控制方法的有效性.
关键词 电磁卫星编队;重构控制;电推进;碰撞规避;近地轨道
中图分类号 V439.4;V448.2
文献标志码 A
0 引言
与价格昂贵、结构复杂的卫星相比,小卫星编队具有低成本、高性能和灵活性强等优点,已获得广泛应用.近年来,小卫星编队已成为空间动力学和控制领域的热门课题.大多数研究者关注利用天然地磁场的电磁力进行近地轨道的小卫星编队飞行,包括洛伦兹卫星编队和电磁卫星编队[1].Peck[1]首先提出了洛伦兹卫星编队的概念,Mai[2]分析了地球低轨的电磁卫星编队飞行的动力学和控制方法.洛伦兹卫星是一种带静电的航天器,它可以通过与周围磁场的相互作用,为轨道机动诱导洛伦兹加速度[3].洛伦兹航天器通过无推进剂电磁推进,可实现航天器交会[4-5]、航天器悬停[6-8]、编队飞行[9-11],以及行星捕获和逃逸[12-13]、轨道倾角控制[14]等多种应用[15].
学者们分析了地轨附近的小卫星编队飞行的动力学模型及编队控制方法.文献[16]研究了卫星间电磁力的最优重构轨迹和重构控制,基于Tschauner-Hempel方程构建了非线性动力学模型,采用高斯伪谱方法,通过数值模拟验证,实现了最优控制.文献[17]分析了洛伦兹卫星编队动力学模型,提出一种无推进的闭环控制方法并通过数值仿真进行了验证.尽管已有文献讨论了各种各样保持编队飞行的控制方法,但对动态碰撞规避过程的重构控制研究较少.
在地球低轨附近有许多废弃的卫星和空间碎片,这对在轨飞行卫星编队构成了潜在威胁.因此,有必要研究电磁卫星编队为实现碰撞规避的重构控制方法.假设地球磁场是一个随地球旋转的倾斜偶极子,通过地球磁场与装有电磁线圈的磁性卫星的相互作用,可以很容易实现稳定的编队控制.但是,电磁卫星之间的相互作用力是一种内力,不能改变电磁卫星编队质心的初始动量,必须通过外部推进来完成实际碰撞规避过程以满足所需的转向力.Saaj等[17]首先提出了库仑卫星编队采用电动推进器和库仑推进的混合推进下的碰撞规避方案.Wang[18]将多模霍尔推力器成功地应用于碰撞过程中,为地球静止轨道附近的库仑卫星编队提供外部推力.基于笔者前期工作,本文采用霍尔推力器P-70作为电磁卫星编队碰撞规避过程的外部推进,采用基于模糊推断的LQR控制方法设计了碰撞规避过程的重构控制.
1 电磁卫星编队的相对动力学模型
电磁卫星组成的卫星编队中,通过给卫星中线圈充电产生磁偶极子,如图1所示.假设由两颗电磁卫星组成的编队中,其线圈分别是a和b,通过线圈的电流和偶极子的方向如图1所示,偶极子的强度定义为μ=NiS,其中N表示绕线匝数,i是流过线圈的电流,s表示线圈的面积,为单位方向向量.
对于给定的坐标系ox′y′z′,d是偶极L和偶极F中心之间的距离,α和β是绕轴旋转的偶极的旋转角,θ和φ是绕x′轴旋转的偶极子的旋转角.偶极L和偶极F的强度矢量如下:
μL=(μLcosα)x′+(μLsinαcosθ)y′+(μLsinαsinθ)z′,
OZ是沿着地球自转轴指向北极的,主星坐标系的原点与主星的质心重合,OX轴从地球中心指向主卫星的轨道平面,OY轴的方向指向正方位角,OZ轴与OX和OY构成右手坐标系.对于地心惯性,主星和第i个从星的动力学方程分别写为
2 改进的多模霍尔推力器及LQR重构控制
如果障碍物突然出现在电磁卫星编队飞行的轨道上,则会造成与从星的碰撞.为实现碰撞规避将此过程描述为从星从当前轨道向更高轨道移动,而主星保持其位置.即通过增大主从星之间的编队距离,可以避开障碍物.在此过程中,第i个跟踪卫星的状态变量Xi=[xi,yi,zi,〖AKx·〗i,〖AKy·〗i,〖AKz·〗i]T,为实现碰撞规避的期望位置为Xdi=[xdi,ydi,zdi,〖AKx·〗di,〖AKy·〗di,〖AKz·〗di]T.此过程中扰动定义为D=[dx,dy,dz]T,系统输出Y=[xi,yi,zi]T,则系统状态方程可写为
可以看出系统是渐近稳定的.
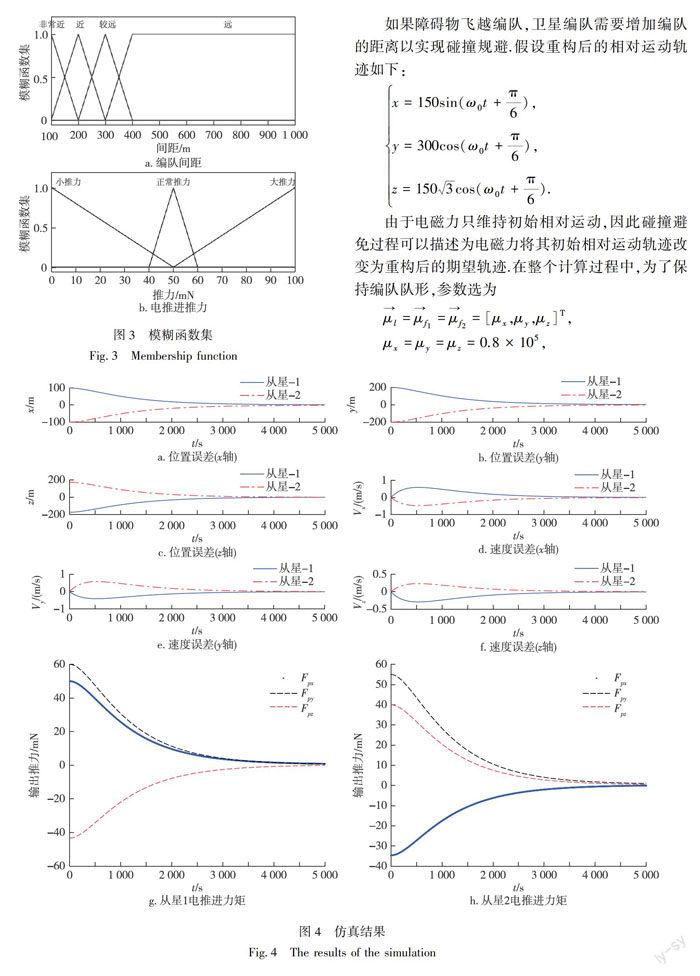
基于李雅普诺夫稳定性理论,e全局收敛到0.利用LQR设计的控制器可以实现电磁卫星编队的重构控制.然而,由于控制律完全由系统状态方程和重构时间决定,而电推进的推力完全由参数Q和R的选择决定,如果考虑变量信息,控制器在重构过程中能更好地满足编队的自治性要求.为了增加自主性,设计了一种模糊逻辑控制器来改变和调整LQR控制器的性能.模糊逻辑系统采用位置误差和电动力系统的输入作为控制系统的输入.模糊集的选取如图3所示.通过选择4组Q和R的值,控制增益K的取值分为4种情况:极小推力(B)、小推力(W)、中等推力(Z)和较大推力(D).
〖PSXX19210.eps;X*3,BP#〗
3 仿真结果及分析
本文采用了一颗主星和两颗从卫星组成的电磁卫星编队.主导卫星围绕着半径为7 000 km的圆形轨道飞行,两颗从卫星位于主导卫星的两侧,它们共享围绕主星飞行的相同轨道,如图2所示.主星和两颗从星都装有三维磁偶极子.假设两颗从星的磁偶极子间无相互作用,初始形成的相对运动轨迹为
由于電磁力只维持初始相对运动,因此碰撞避免过程可以描述为电磁力将其初始相对运动轨迹改变为重构后的期望轨迹.在整个计算过程中,为了保持编队队形,参数选为
μl=μf1=μf2=[μx,μy,μz]T,
μx=μy=μz=0.8×105,
μe=3.986 5×1 014,
ml=mf1=mf2=100,
Fd=[-1.027,6.3,-2.5]×10-5,
Q=diag[1,1,1,100,100,100],
R=diag[0.01,0.01,0.01],
ρ=3×104×I3×3,
φ0=2×103.
从星的初始和最终状态为
Xf10=[50,100,86.6],
Xf1d=[150,300,259.8],
Xf20=[-50,-100,-86.6],
Xf2d=[-150,-300,-259.8].
其中μx、μy、μz单位为A·m2,μe单位为m2·s-3,Fd单位为N,Xf10、Xf1d、Xf20、Xf2d的单位均为m.
仿真结果如图4所示.图4a、4b和4c显示了初始轨迹和从星的期望轨迹之间的位置误差.图4d、4e和4f显示了初始轨迹和从星期望轨迹之间的速度误差.图4g和4h显示了从星电推进在x轴、y轴和z轴的推力大小.从仿真结果可以看出,电磁卫星编队实现了碰撞规避重构过程.
4 结论
本文首先分析了两颗电磁卫星的相对运动动力学模型,然后,阐述了基于模糊推理的LQR重构控制方法.通过模糊推理系统,电推进可以根据实际编队的距离自动调整输出推力以提供电磁卫星编队在碰撞规避过程中的转向需要.最后,通过数值仿真进行了验证.
参考文献
References
[1] Peck M A.Prospects and challenges for Lorentz-augmented orbits[C]∥AIAA Guidance,Navigation,and Control Conference and Exhibit,San Francisco,CA,2005:15-18
[2] Mai A U.Dynamics and control of electromagnetic formation flights in low each orbits[C]∥AIAA Guidance Navigation,and Control Conference and Exhibit,Keystone,Colorado,2006
[3] Pollock G E,Gangestad J W,Longuski J M.Analytical solutions for the relative motion of spacecraft subject to Lorentz-force perturbations[J].Acta Astronautica,2011,68(1/2):204-217
[4] Yamakawa H,Bando M,Yano K,et al.Spacecraft relative dynamics under the infuluence of geomagnetic lorentz force[C]∥Aiaa/aas Astrodynamics Specialist Conference.2013
[5] Huang X,Yan Y,Zhou Y,et al.Improved analytical solutions for relative motion of Lorentz spacecraft with application to relative navigation in low Earth orbit[J].Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2014,228(11):2138-2154
[6] Huang X,Yan Y,Zhou Y.Dynamics and control of spacecraft hovering using the geomagnetic Lorentz force[J].Advances in Space Research,2014,53(3):518-531
[7] Huang X,Yan Y,Zhou Y,et al.Sliding mode control for Lorentz-augmented spacecraft hovering around elliptic orbits[J].Acta Astronautica,2014,103:257-268
[8] Peck M A,Streetman B,Saaj C M,et al.Spacecraft formation flying using Lorentz forces[J].Journal of the British Interplanetary Society,2007,60(7):263-267
[9] Tsujii S,Bando M,Yamakawa H.Spacecraft formation flying dynamics and control using the geomagnetic Lorentz force[J].Journal of Guidance,Control,and Dynamics,2013,36(1):136-148
[10] Sobiesiak L A,Damaren C J.Optimal hybrid control for Lorentz-augmented formation flying[C]∥AIAA Guidance,Navigation,and Control Conference,Boston,MA,2013:19-22
[11] Huang X,Yan Y,Zhou Y.Optimal spacecraft formation establishment and reconfiguration propelled by the geomagnetic Lorentz force[J].Advances in Space Research,2014,54(11):2318-2335
[12] Gangestad J W,Pollock G E,Longuski J M .Lagranges planetary equations for the motion of electrostatically charged spacecraft[J].Celestial Mechanics and Dynamical Astronomy,2010,108:125-145
[13] Gangestad J W,Pollock G E,Longuski J M.Analytical expressions that characterize propellantless capture with electrostatically charged spacecraft[J].Journal of Guidance,Control and Dynamics,2011,34:247-258
[14] Pollock G E,Gangestad J W,Longuski J M.Inclination change in low-earth orbit via the geomagnetic Lorentz force[J].Journal of Guidance,Control,and Dynamics,2010,33(5):1387-1395
[15] Huang X,Yan Y,Zhou Y,et al.Output feedback control of Lorentz-augmented spacecraft rendezvous[J].Aerospace Science and Technology,2015,42:241-248
[16] Cai W W,Yang L P,Zhu Y W,et al.Optimal satellite formation reconfiguration actuated by inter-satellite electromagnetic forces[J].Acta Astronautica,2013,89:154-165
[17] Saaj C M,Lappas V,Schaub H,et al.Hybrid propulsion system for formation flying using electrostatic forces[J].Aerospace Science and Technology,2010,14(5):348-355
[18] Wang T.Collision avoidance of Coulomb spacecraft formations using multi-mode hall thrusters[J].Aerospace Science and Technology,2017,68:261-268
Applying electric propulsion to collision avoidance process
in electromagnetic formation flight
BAI Jing1 WANG Ting1
1 School of Instrument Science and Engineering,Southeast University,Nanjing 210096
AbstractElectromagnetic formation flights(EMFFs) can be stabilized in low Earth orbit owing to the influence of Earths magnetic field.Formation control is realized by changing the current magnitude of the magnetic pole of the EMFF.Although Earths magnetic field is generally considered to be a dipole and rotates with Earth,the interaction between the magnetic fields of Earth and the EMFF is considered to be an internal force.When a small magnetic satellite formation encounters an obstacle that must be avoided,the current magnetic force,which acts as an internal force,cannot promote directional changes.Therefore,it is necessary to exert external forces on the EMFF to gain control.As a continuation of the application of electric propulsion (EP) to Coulomb satellite formation,this study investigates how EP may be applied to collision avoidance by EMFFs.During the process,the external thrust of the EMFF was provided by EP,which served as supplementary propulsion to realize obstacle avoidance.EP adopted multimode Hall thrusters,and a linear formation was employed by the EMFF.Using the linear quadratic regulator control method with an added fuzzy reference system,EMFF achieved collision avoidance with numerical simulation.
Key wordselectromagnetic formation flights;reconfiguration control;electric propulsion;collision avoidance;low Earth orbit
