如何从“冷饭”到“营养餐”

陈小燕

【摘 要】新课标从实验稿到2011版，在“统计与概率”部分的调整包括容量减少和难度降低，与拉长和增加统计的学习，可能性即概率知识的学习，仅仅安排了一次学习。这部分内容该如何复习？丰富素材网罗多种概率模型，积累活动经验，加强数据分析方法的指导，只有指向学科素养的教学才具有生命力。

【关键词】实验;体验;数据分析

虽然几年没教六年级了，这学期却有幸思考了六年级的一节“可能性”的复习课。备课时所见的仅仅是苏教版六年级教材中的一页复习内容，追溯苏教版的教学内容，仅仅在四年级上册进行过一次小单元的教学。不禁思考，仅教过一次，复习是否是将那盘新授的“冷饭”炒炒就好？答案显然是否定的，从四年级到六年级，学生已经逐步形成了抽象思维，思维水平不同，对知识应当有更深刻的认识和理解。同时，六年级的复习是对整个小学阶段数学学习的一个总结，同时也即将开启第三学段数学的学习，具有承前启后的作用。所以，我们需要站在更高的角度进行思考。仔细阅读那一页的复习内容：前两题是基础练习，复习简单随机事件的特点，通过列举判断简单随机事件发生的可能性的大小;第三题则是综合运用可能性的知识解决实际问题;第四题则一反常序由摸球结果倒推球的组成，意在感受简单随机事件发生的可能性与事件发生频率之间的联系。不难窥见复习思路：基础—应用—深化，正如教材只是一个例子，不同的人有不同的理解，教无定法，针对同样的教学内容，我们需要充分发挥复习效用，将一盘冷饭变成营养餐呢？笔者有了如下的思考。

一、丰富素材——将“冷饭”炒热

小学阶段的数学教学，要通过重复试验让学生估计随机事件发生的可能性大小。教材中，无论是苏教版、浙教版还是北师大版，尽管编排不同，但都涉及了抛硬币、掷骰子、摸球、玩转盘等多种实验素材。这些不同的实验素材，其实属于不同的概率模型，其中转盘属于几何概型，其余属于古典概型。几何概型是连续的，可以分为无限等份，能形象直观地帮助学生理解可能性的大小;古典概型则可能结果有限，是较为具体的模型。但这两种模型都属于理论概率模型，它们出现的可能性相等。其中，抛硬币是结果最为简单的等可能性模型，所以，比赛选场地常用这类简单方便的方法。

但是，仅仅这样的概率模型并不够，生活中仍存在很多非等可能性的随机事件，而这样事件可能性的大小更依赖与对实验数据的统计。对比苏教版、浙教版、北师大三个版本，北师大版中有所体现，具体的有抛啤酒瓶盖、天气情况预测等。由于等可能性事件的结论较为明显，经常让学生失去实验兴趣;非等可能性事件对实验的依赖，能帮助学生更好地理解随机性。同时，对于可能性的判断原自统计数据的分析，更能体现统计与概率二者之间的紧密关系。

不同的概率模型对学生理解可能性具有不同的帮助，丰富的素材网罗了多种概率模型，能帮助学生夯实基础。

二、让定性飞一会儿——将“冷饭”炒熟

新课标从实验稿到2011版，在“统计与概率”部分的调整包括容量减少和难度降低，与拉长和增加统计的学习，如扇形统计图的学习更为具体，却减少了可能性即概率知识的学习，仅安排了一次学习。随机思想是概率教学的核心，正所谓离开了随机，就谈不上概率。中科院院士陈希孺先生认为：统计学是有关收集和分析带随机性误差的数据的科学和艺术。统计并非一成不变，应渗透随机性，感受不确定事物远远多于确定事物，接纳不确定性的存在。随机思想的渗透应当贯穿于整个“统计与概率”部分，不仅在可能性的那一次学习时，同样，随机思想也是沟通统计和概率的桥梁。

六年级学生在学习了分数百分数后，对可能性大小的表示能述诸于数，能简单地用0、100%表示极端可能情况，理解可能性大小处于极端之中;即使不作定性要求，部分学生也能用分数表示可能性的大小。但苏教版教材对可能性的大小仅限定性描述而不要求定量表示，则是要拉长对随机性的体验。因为不管可能性是大是小，一切皆有可能，在于结果的不确定性，学习的难点则在于对随机性的理解。随机性至少应该包括两个方面：（1）单一事件的不确定性和不可预见性;（2）事件在经历多次重复实验中所表现出的规律性。看似简单，认可却很困难。即使是一些教师，没有接受随机思想，在课堂实验中出现“意外”时，也总是手足无措。

可能性的大小，具体是多少可以缓一缓，过早定量看似进入了更高阶的概率学习，实质是缩短了学生对随机思想理解、内化的过程。让定性飞一会儿，让学生亲临随机环境，亲自试验和收集随机数据，经历统计过程，从而丰富对随机现象的认识，积累大量的活动经验，体会随机思想，让随机思想煸熟我们的冷饭。

三、指向学科素养——将“冷饭”炒香

数据分析作为数学学科素养的重要方面，在小学数学教学中也有所体现。数据分析观念包含三类思想：（1）整体思想：从整体上观察、研究和把握数据;（2）随机思想：认识不确定性的普遍存在，通过偶然发现必然;（3）相对思想：任何结论都相对于一定的条件，统计的方法没有对与错，只有好与不好。《课标（2011版）》将“统计观念”修改为“数据分析观念”，增补了对随机思想的要求：通过数据分析体验随机性，一方面，对于同样的事情，每次收集到的数据可能不同，另一方面，只要有足够的数据就可能从中发现规律。因此，在可能性的教学中，在实施概率实验和感悟随机性的同时，应注重对上述三类思想的渗透，从而提升学生的数据分析素养。

苏教版教材重视数据的分析和推测，四年级上册“可能性”单元最后部分的“动手做”，即是由实验结果推测球的组成的活动。在六年级可能性复习的第4题，则是升级版，将两色球换成了三种花色的扑克牌。但是，由于同一副牌中每张牌都有区别，所以尽管花色不同，但同花色的扑克牌由于数不同，也有差别，所以看似三类的不同组合，其实是6个单一个体，所以，多次实验结果后，学生记住出现过的扑克牌，推测反而变得简单了。于是，复习中还是将扑克牌换成了三种不同的颜色的球共6个，让学生更多关注实验的整体数据，而不仅是每次出现的具体情况，通过有限次（30次）的实验来推测球的组成。

应当说这样的推测活动非常必要，生活中很多隨机事件，例如，抛瓶盖和天气预测，没有准确的计算结果，只能通过大量的数据得到随机事件出现的频率去估计概率，这样的推测活动具有重要的现实意义。但是，学生的数据分析水平如何呢？笔者进行了上述实验。

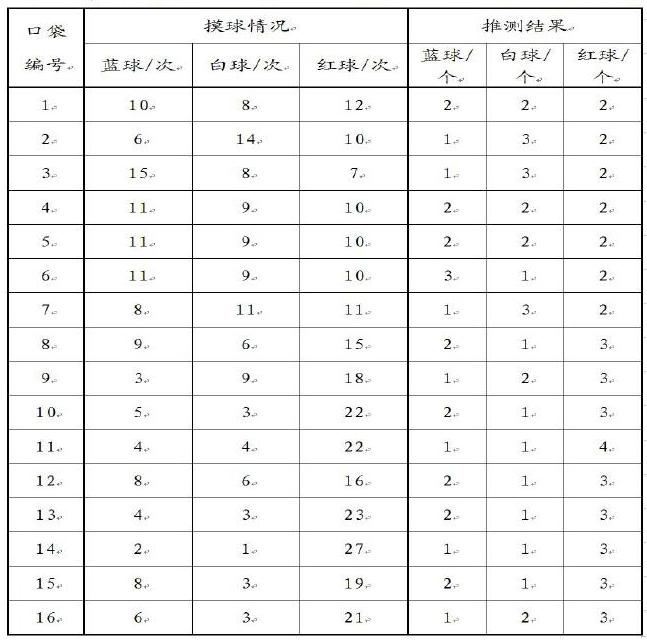
由于课堂时间所限，笔者仅安排了两类组成，共16组：第1-8组，袋中有篮球2个、白球2个、红球2个;第9-16组，袋中有篮球1个、白球1个、红球4个。每组进行30次有放回的摸球，推测袋中球的组成。16组的活动数据如下：

1-8组中推测正确的有3组，占37.5%;9-16组中推测正确的有1组，占12.5%。仔细分析推测错误的数据，有摸球结果随机性导致推测困难的原因，也有数据分析不得法，导致推测错误的原因。例如，4、5、6组摸球结果相同，但是第6组却推测错误，是因为使用了相差法，同时也体现了该组同学对随机性认识不足。从整体16组来看，相对于用比来解释数据的关系，更多小组倾向于用相差关系分析数据，这也是目前大部分学生的数据分析水平。所以，教学中教师需加强对学生数据分析方法的指导，只有指向学科素养的教学才具有生命力，才能让这盘冷饭既香又有营养。

纵观数学史，统计学是一门古老的学问，迄今已有2300多年的历史，而概率论则是一门新兴科学，至今还不到400年。人类的发展尚需孕育这么多年，个体的成长总与历史相像，所以，“可能性”复习内容虽少尤多，需要教师在教学中更有意识地渗透，帮助学生跨越这漫长的历史发展过程，更深入地接纳概率知识。

【参考文献】

[1]陈希孺.机会的数学[M].北京：清华大学出版社，2000：60