床面总阻力系数的研究及应用
2019-05-29李瑞杰李玉婷张义丰
王 彦,李瑞杰,李玉婷,侯 堋,张义丰
(1.河海大学 海岸灾害及防护教育部重点实验室,江苏 南京 210098;2.南京师范大学 虚拟地理环境教育部重点实验室&大规模复杂系统数值模拟江苏省重点实验室&江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023;3.珠江水利科学研究院,广东 广州 510611;4.交通运输部天津水运工程科学研究院,天津 300456)
引 言
阻力特性问题是河口海岸及河流动力学研究的基本问题之一,反映了水流对底床作用力的大小,决定了底床泥沙的运动强度,直接关系到水流挟沙力的计算结果。天然实测资料直接反映的是床面总阻力,而在水流挟沙力计算公式中,阻力系数的选取一般都忽略了沙波阻力的影响,因此将考虑了沙波阻力的床面总阻力系数应用于一般形式的挟沙力计算公式中,可提高挟沙力计算公式的精确度,具有一定的应用价值。本文对目前常用的沙粒阻力及沙波阻力的计算公式进行分析,提出了更为简洁的总阻力系数计算公式,利用近岸实测数据进行验证分析,并将其与郭俊克[2]的床面总阻力系数公式进行对比。
1 传统总阻力系数计算方法
目前人们对总阻力系数的研究,大致分为2类:
1)直接计算总阻力系数,以钱宁-麦乔威、吉川秀夫、李昌华-刘建民等[3]的成果为代表;
2)根据作用单元的不同,分别计算沙粒阻力系数和沙波阻力系数,而后叠加求和,以Einsterin和Barbarossa[4]、Engelund[5-6]等人的成果为代表。
大多学者的阻力公式建立于水槽实验和河流基础上,且以往基于方法 2)的研究主要限于经验研究,将总阻力分成沙粒阻力和沙波阻力并分别在试验中测量,如Raudkivi、Vanoni和Huang、Rifai和 Smith、Vittal等、Wang及 Fehlman等[7],而郭俊克[2]根据流体力学中边界层理论的基本原理,从理论上给出了沙粒阻力与形状阻力的计算公式,叠加所得的总阻力系数计算公式精确度较高。下面对几种传统的总阻力系数计算方法进行总结分析。
1.1 水力半径分割法
H.A.Einstein和N.L.Barbarossa[4]基于水流泥沙条件的方法,采用水力半径分割法,将水流中单位水体消耗的时均能量分为两部分,分别对应沙粒阻力和沙波阻力。按照剪切应力叠加可以表示为:
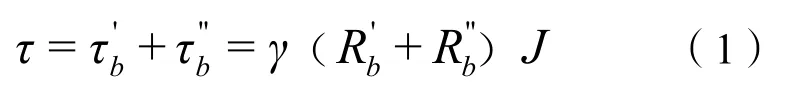
式中:τ为总阻力对应的剪切应力,分别为沙粒阻力和沙波阻力对应的剪切应力;和分别为对应于这两者的水力半径;γ为水的容重,J为能坡。其中:



则总阻力系数fb的计算公式为:

1.2 能坡分割法
F.Engelund[5-6]基于水流泥沙条件的方法,采用能坡分割法,假定J=J'+J",并将床面总剪切力表示为:

式中:J'和J"分别对应沙粒阻力损失和沙波阻力损失所引起的能坡。
F.Engelund假定对宽浅河道有R≈h,则式(6)可表示为:

由此,F.Engelund定义相应于总阻力、沙粒阻力和沙波阻力的Shields数分别为:

其中,总阻力Shields数θ、沙粒阻力Shields数θ'及沙波阻力Shields数θ"分别表示为:

其中,Δ为沙波波高,Fr为弗汝德数。
1.3 公式的修改和扩展
J.Fredsoe和R.Deigaard在F.Engelund[8]的研究基础上,对总阻力系数的计算公式又进行了修改和扩展,如下所示:


式中:s为比重,s=γs/γ,γs为泥沙容重,γ为水的容重;Δ为沙波波高,单位为m;λ为沙波波长,单位为 m;h为平均水深,单位为 m;U为平均流速,单位是 m ⋅ s-1,其计算公式如下:
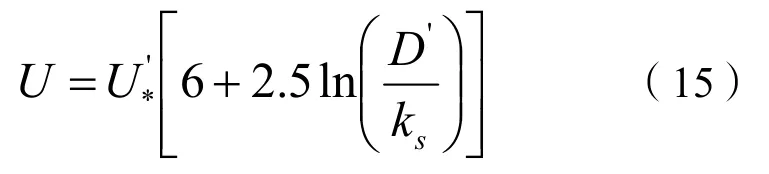

沙波波高和波长是一个与中值粒径有关的函数,沙波尺度Δ和λ可以通过下式估算[9]:

则总阻力系数fb的计算公式为:
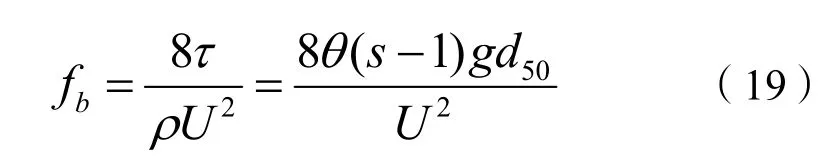
1.4 基于沙波几何形态的方法

图1 沙垄形状及水流现象示意
郭俊克[2]基于沙波几何形态的方法认为,实际沙波具有三维性、移动性、不规则性,难以精确地进行理论分析,因此,为方便研究,将实际沙波床面简化为二维固定三角形沙波床面,如图1所示。
图1中:Δ为沙波波高;h平均水深;λ为沙波波长;h1为沙波波峰断面水深;U为平均流速;h2为沙波波峰断面水深;lw为漩涡长度;y0为沙波河床的理论床面;h1+yo=h2+Δ。
各水力要素的大小可直接由沙波河床的理论床面的位置决定,其中包括沙波波峰断面水深h1、沙波波谷断面水深h2等。Engelund等[10]、Engel[11]以及 Shen等[12]认为,可用沙波波高的一半代替沙波河床的理论床面位置y0,即:

则沙波河床的波峰断面水深h1及波谷断面水深h2的计算公式为:
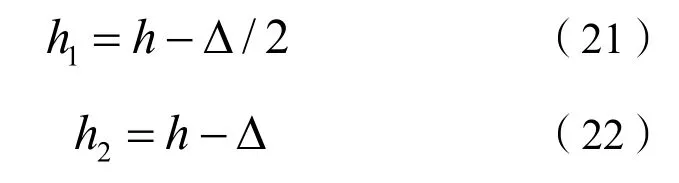
关于漩涡长度lw,本文采用郭俊克[13]的经验公式确定:
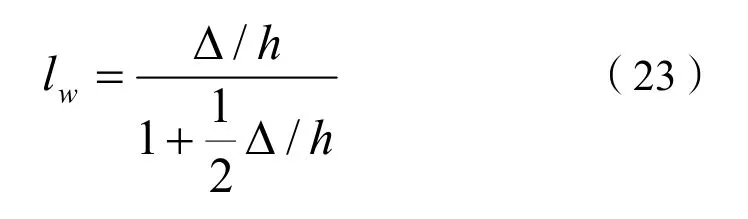
沙波波高Δ和波长λ分别采用式(17)和式(18)估算[9]。
综上,导出的沙粒阻力和沙波阻力的理论推导公式分别为:

则总阻力系数的计算公式为:

2 总阻力系数公式的简化形式
影响总阻力系数的因素众多[14],计算公式结构多样,很多因素难以直接测量确定,计算公式缺少实用性,为挟沙力的计算造成了诸多不便。因此,有必要提出更简洁的总阻力系数公式,为近岸挟沙力的简便计算提供条件。
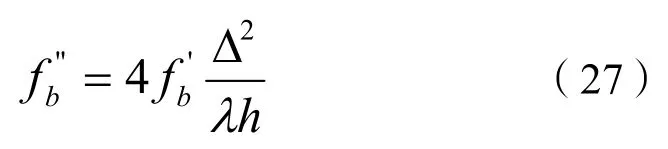
其中,沙波波高Δ和波长λ分别采用式(17)和式(18)估算[9],则总阻力系数的计算公式为:
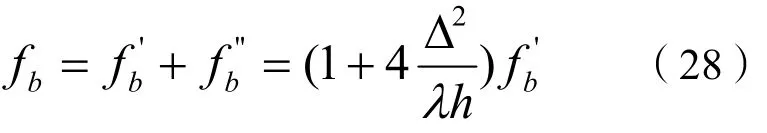
3 阻力系数计算公式在挟沙力计算中的应用
水流挟沙力问题的理论研究在泥沙研究领域非常重要,李瑞杰等[16]将浑水异重流动量方程延拓到整个含沙水流水深范围,推出稳定条件下平衡含沙量表达式,并采用水流最小能耗率原理得到一般形式的挟沙力公式:
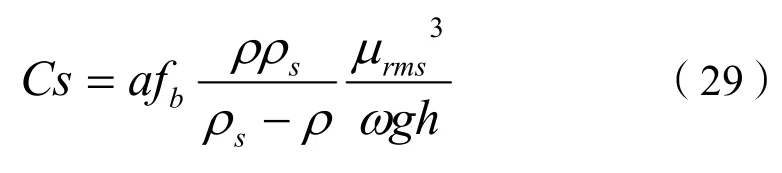
式中:Cs为水流挟沙力,单位为 kg⋅m-3;α为常数;ρs=2650kg⋅m-3,为泥沙颗粒的密度;ρ=1000 kg⋅m-3,为水体的密度;ω为泥沙沉速,单位为m⋅s-1;fb为阻力系数;g为重力加速度;h为水深;urms为如下式定义的有效流速:

式(30)中:ui为实测垂向(或垂线)平均流速,单位为 m/s;N为实测垂向(或垂线)平均流速的总个数。
本文分别将简化的总阻力计算公式、郭俊克[2]总阻力计算公式及其沙粒阻力系数计算公式代入到一般形式的挟沙力公式中,采用连云港近岸实测数据对式(29)进行验证分析,验证情况如图2和图3所示。由图可知,三者实测值与计算值吻合度较高。实测资料中,近岸泥沙粒径的范围为0.005~0.009 mm,近岸实测数据均包含大、中、小潮过程,有效速度由对应的完整潮周期内的实测流速计算得到。

图2 不同公式计算的近岸水流挟沙力验证结果1
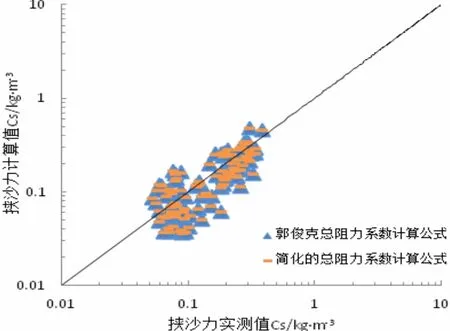
图3 不同公式计算的近岸水流挟沙力验证结果2
采用平均绝对误差MAE、均方根误差RMSE和符合指数Ic[17]对应用三种公式后的挟沙力计算结果与实测数据进行比较分析:
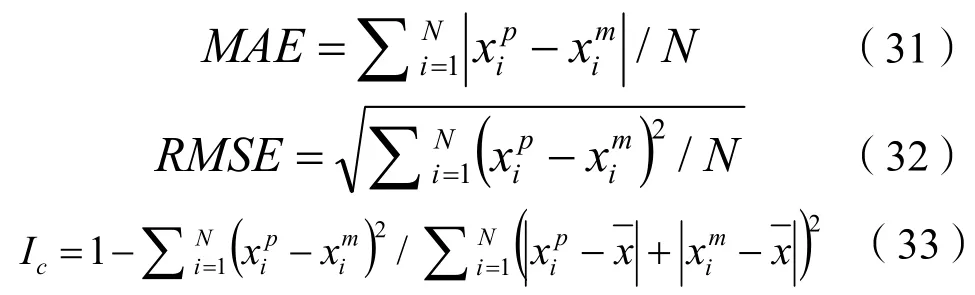
3.1 简化总阻力系数和沙粒阻力系数计算公式对比
本文分别将简化的总阻力系数表达式(28)和未考虑沙波阻力的阻力系数表达式(25)应用于一般形式的挟沙力公式(29)中,采用论文选取的样本数据,计算MAE、RMSE和Ic,统计结果见表1。

表1 计算值与实测值结果对比
由表1可知,在一般形式的水流挟沙力公式的计算中,与应用仅考虑沙粒阻力而未考虑沙波阻力的阻力系数公式相比,应用简化的总阻力系数公式后,水流挟沙力计算结果的平均绝对误差和均方根误差均较小;由符合指数来看,考虑沙波阻力后,水流挟沙力计算公式的符合指数Ic值有所提高。
3.2 总阻力计算公式的应用对比
本文分别将简化的总阻力系数表达式(28)和未简化的郭俊克总阻力系数表达式(26)应用于一般形式的挟沙力公式(29)中,采用论文选取的样本数据,计算MAE、RMSE和Ic,统计结果见表2。

表2 计算值与实测值结果对比
由表2统计结果可知,分别应用简化的总阻力系数公式和郭俊克总阻力系数公式于一般形式的水流挟沙力公式的计算中,可发现:水流挟沙力计算结果的平均绝对误差和均方根误差均较小且较为接近;从符合指数来看,应用二者后水流挟沙力的计算结果的符合程度均较好且Ic值近似相等,分别为0.89352和0.89355(Ic为1表示计算值和实测值完全符合)。
4 结 论
本文简述了几种传统总阻力系数的计算方法,通过综合考虑沙粒阻力及沙波阻力的影响,提出了更为简洁的总阻力系数计算公式,对比分析了沙波阻力对水流挟沙力计算的影响,并将简化的总阻力系数计算公式与郭俊克的床面总阻力系数公式应用于一般形式的水流挟沙力计算公式中,比较分析该简化公式的准确性和实用性。主要结论如下:
1)将简化的床面总阻力系数计算公式应用于近岸水流挟沙力计算公式中,其实测值与计算值吻合度较高。
2)应用综合考虑沙粒阻力和沙波阻力的床面总阻力系数所得的近岸水流挟沙力计算结果,其精度较仅应用沙粒阻力系数所得的近岸水流挟沙力计算结果有所提高,但提高程度相对较小,说明沙波阻力对水流挟沙力计算的影响较沙粒阻力小。
3)简化的床面总阻力计算公式与郭俊克计算公式的计算结果精确度相差不大,可为近岸挟沙力简便计算提供条件,具有一定的工程应用价值。
