随机纵浪中多自由度耦合的船舶横摇运动研究

周光耀，唐友刚，王丽元，李 妍

（1.天津大学 建筑工程学院，天津 300072；2.天津大学 水利工程与仿真国家重点实验室，天津 300072）

引 言

参数横摇是造成船舶的倾覆的主要原因之一，是近年来船舶稳性和耐波性领域研究的热点。

船舶参数激励问题早在1955年就被Kervin提出，20世纪 80年代，B.Roberts和 A.Bruce Dunwoody等首次对随机参激横摇进行了概率分析[1,2]。1998年，巴拿马型 C11级集装箱船 APL CHINA号事故引起了学者对参数横摇的重大关注[3]。由此国内外学者开始了对参数横摇进行了大量理论和实验方面的研究。早在20世纪90年代，天津大学唐友刚、郑俊武、田凯强等就研究了船舶横摇与纵摇、升沉的耦合[4,5]。李红霞于2007年对船舶参数横摇进行了时历运动计算和概率分析[6]。鲁江对于纵向行驶在具有随机性质波浪中的航行体的横向摇动和波浪对于船舶的附加外力做出了数值上的模拟和探索[7,8]。2015年，张晓等从参数敏感性的角度对航行在具有随机性质波浪中的船舶的横向摇摆进行了探索[9]。同时国外学者也做了大量工作。Bulian等人对于船舶性质参数和运动的随机性质进行了探索[10,11]，他们的探索对象亦是纵向行驶在具有随机性质的波浪中的航行体；2009～2011年，Jovanoski Z、Atsuo Maki等均对纵向行驶在随机环境中的航行体的运动概率特性和力学特性进行了探索[12,13]。

从以上一些研究现状来看，对于船舶在随机波中的多自由度耦合的运动分析和船舶在随机波中的横摇角概率分布研究较少。且多是利用欧拉旋转矩阵对船舶多自由度运动进行研究。本文利用瞬时等效旋转矩阵推导出考虑多自由度同时运动的运动方程，在此基础上计算实时位置的波浪力。通过无理数分波浪谱模拟随机波，计算实船在时历上的运动响应。并进一步其进行力学分析，分析运动不稳定性和混沌产生的原因。同时对多组计算结果进行直方图统计和概率密度函数的模拟。创新引入风险评估与数学函数模拟相结合的思想，研究船舶在随机波中的横摇角概率。并深入研究，推导出研究其横摇概率的广义方法，拟合得到以波高和横摇角为自变量的三维概率分布函数。以此估算任意波高下发生某个横摇角度的概率。

1 坐标系的建立及瞬时等效转换关系

1.1 坐标系的建立

坐标系的选取与船舶运动和复原力计算有重大影响，为了方便表述，如图1建立如下坐标描述系统：

1）相对航行体平移的平移坐标描述系统OUxUyUzU（equilibrium coordinate），记号U；

2）OTxTyTzT为联动坐标描述系统（onboard coordinate），记为T，指坐标描述系统随着物体的旋转运动而相应地改变；

3）坐标系Oxyz为恒定的坐标描述系统（fixed coordinate），记为O，指坐标描述系统不随航行体的运动而改变的大地坐标描述系统；

4）相对坐标描述系ORxRyRzR（reference coordinate），记号R。

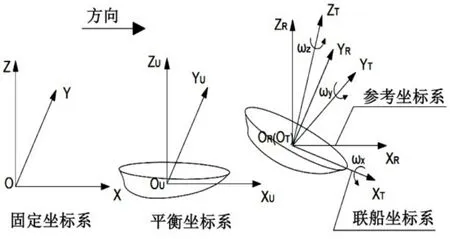
图1 坐标系示意

1.2 坐标系的转换关系

设A为旋转矩阵用以表示T坐标系中的点(x,y,z)与其在R坐标系中(x1,y1,z1)的坐标的关系为：

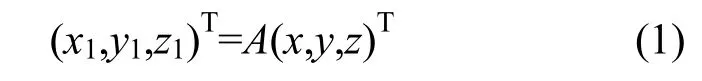
设P(t)为t时刻瞬时（Δt）坐标转换矩阵表示在Δt时刻内的坐标转换关系，则有：

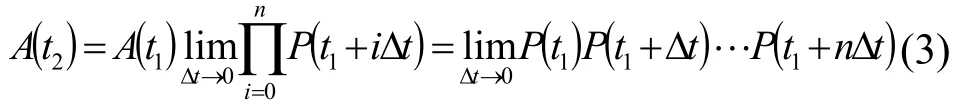
欧拉等效多自由度转动定律：航行体的运动可以通过矢量转换分解为以X、Y、Z轴进行旋转的运动。加入航行体在三维空间中的旋转角速度为ωx、ωy、ωz，则在每一个固定时刻航行体的旋转运动都能够用绕着某条直线l且直线经过坐标系统的原点的单轴旋转运动，其单轴转动角速度为ωl，l与X、Y、Z轴分别成角度α、β、γ，且关系服从式(4)：

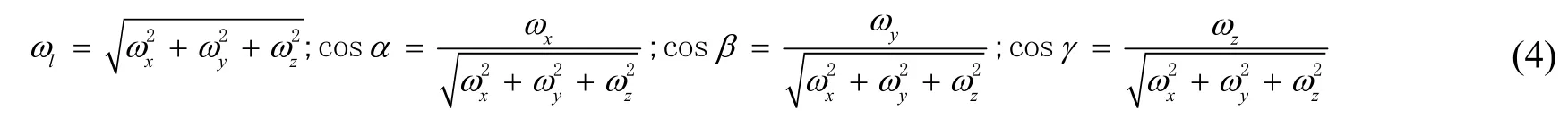
设λ=ωlΔt，则瞬时坐标转换矩阵为：

式(5)的矩阵确保了航行体在空间多自由度中坐标位置的计算是同一时刻的。

2 多自由度耦合运动模型

联动坐标系统的原点可以随意选取，本文取航行体的质量中心。根据航行体的结构特性，我们能够得到xG=yG=zG=Ixy=Iyz=0。考虑航行体在空间中的运动的复杂特性和变系数微分方程的性质，通过基本动力学的推导，笔者建立了航行体的四自由度的运动方程为：

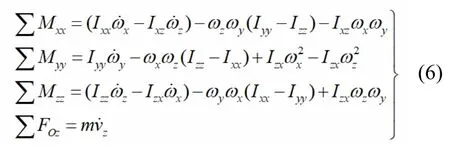
其中，∑Mxx表示关于T坐标系x轴的波浪力的合力矩，∑Myy和∑Mzz类似。∑FOz表示O坐标系中z方向上的合外力，I表示转动惯量。此运动模型不再用欧拉角进行处理，而是通过式(3)和式(5)直接计算实时位置。

3 随机纵浪及其波浪力的处理

设船航行方向为固定坐标系X轴正方向。对于不规则波的模拟利用谱密度函数S(ω)，采用下式[14]：

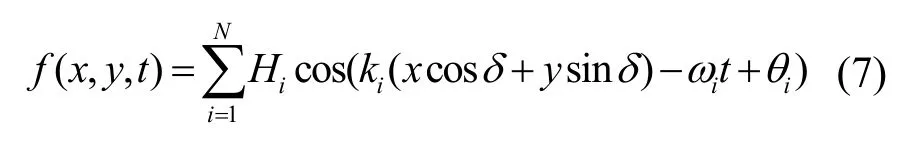
由于各频率是等差数列，在长时间后模拟的波形可能重复。一些处理方法是将频率按波浪谱等面积划分，在实际编程中需用到多次迭代计算各频率。引入无理数采用较为简单的划分方式，如下：

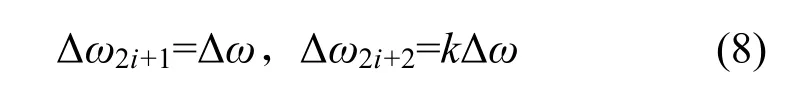
其中k为某无理数。取k为作为一个划分倍数。

对(7)式可得一般的波中水压强为：

其中，ρ为水密度，g为重力加速度。

4 计算实例与分析

4.1 运动结果及力学分析

采用某C11集装箱船为实例研究对象，其主要参数如表1。

表1 C11集装船主要参数

用JONSWAP谱模拟基于随机性质的波浪的谱密度函数，随机参数组数为10，通过正余弦函数的线性和表示基于随机性质的波浪在空间中的形状函数。改变随机因子，对波长接近船长的不同波高的波浪下的运动进行了多组计算。用随船坐标系的z轴与参考系的Oxz平面夹角 Angle表示横摇运动。只给出各个波高下的一组时历运动结果，如图2～图5。

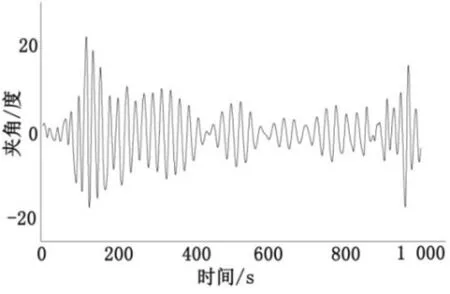
图2 波高2.5 m随机波横摇运动响应

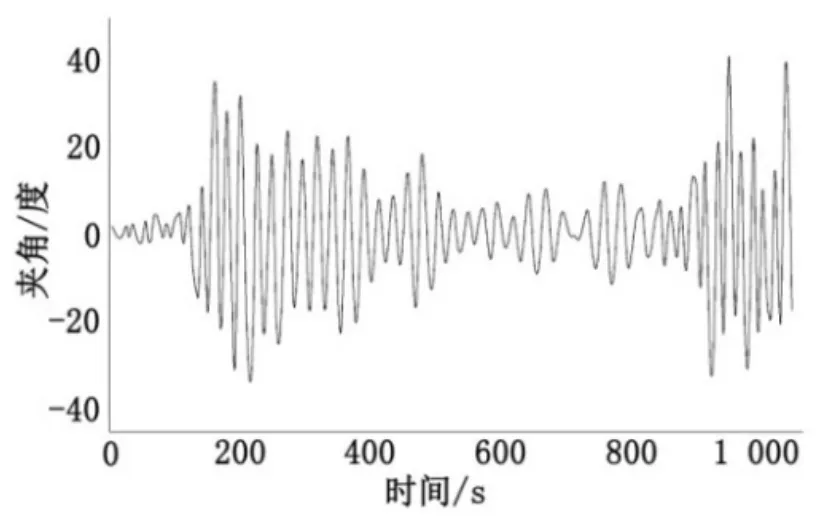
图3 波高3.5 m随机波横摇运动响应

图4 波高4 m随机波横摇运动响应

图5 波高5 m随机波横摇运动响应

在运动的计算中，我们选取了262 m为具有随机性质的波浪的波长，纵向行驶的航行体在具有随机性质的波浪中的航行速度是2 kn，航行体在零时刻的横向转动的角速度是0.01 rad/s。随机波浪在零时刻的相位是通过计算机随机产生的。

从图2～图5的计算结果可以看出，船舶在随机波下的横摇运动是不稳定的。图5和图4比较可以看出，纵向行驶在具有随机性质的波浪的航行体的横向摇摆的幅度最大值和波浪幅度并非是正相关的，这是因为波浪的随机性质存在一定的不确定性和奇异性。但也能够看出航行体在整个横向摇摆系统中的能量与波浪幅度是正相关的。

为了研究其非线性运动的不规则性和运动能量的分布情况，给出图2～图5对应的相图如图6～图9。

图6 波高2.5 m随机波横摇运动相图

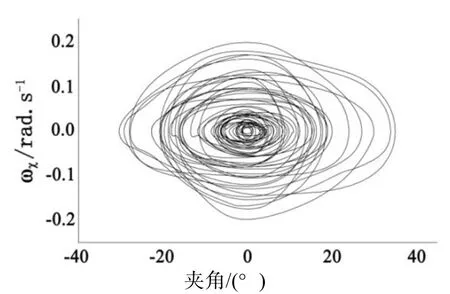
图7 波高3.5 m随机波横摇运动相图

图8 波高4 m随机波横摇运动相图

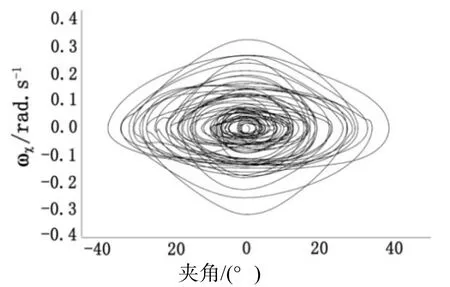
图9 波高5 m随机波横摇运动相图

从图6～图9可以看出，其运动速度极值点在波高2 m是0.1 rad/s左右，到5 m波高时达到0.3 m/s左右。这表明其运动的能量是随波高增大而增大的，这个现象从横摇幅值不能完全断言。船舶横摇运动的能量，主要还是来源于波浪的能量，其中可能有一些转换过程，但最终表现出来的是波浪的能量带动了船舶的横摇。从图6～图9各相图可以看出，在随机波下的参数横摇运动很容易就产生了混沌。观察图8和图9可以发现，运动变得剧烈，相图更是不规则，其运动越是不稳定。其产生的主要原因来自于，大波高情况下船体表面的不规则性表现得更加明显，加上随机波的难以预料性，使其运动更为不稳定。对于各相图的集中区域可以看出，其集中区域是在不断扩大的，这是其分叉运动的一个缩影，也是其运动能量转换的一个标志。

为了研究其混沌运动的内在频率关系，给出各运动的频谱图，如图10～图13。

图10 波高2.5 m随机波横摇运动频谱

图11 波高3.5 m随机波横摇运动频谱

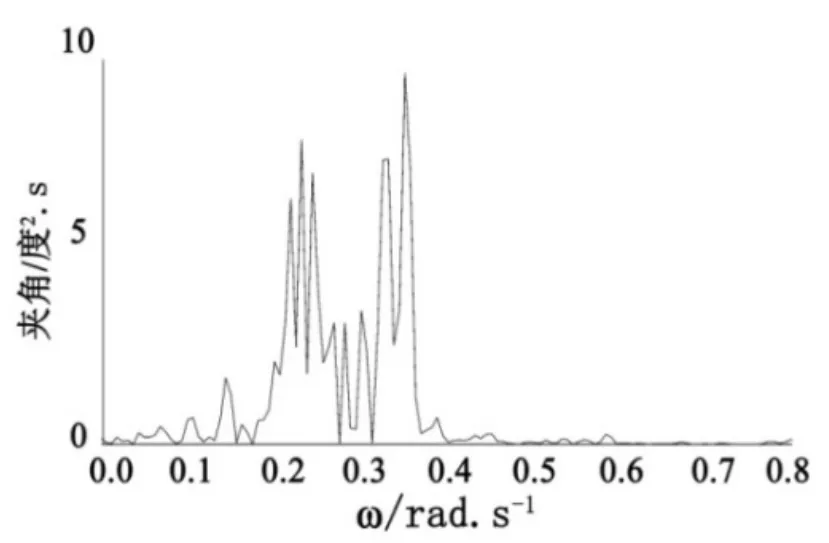
图12 波高4 m随机波横摇运动频谱

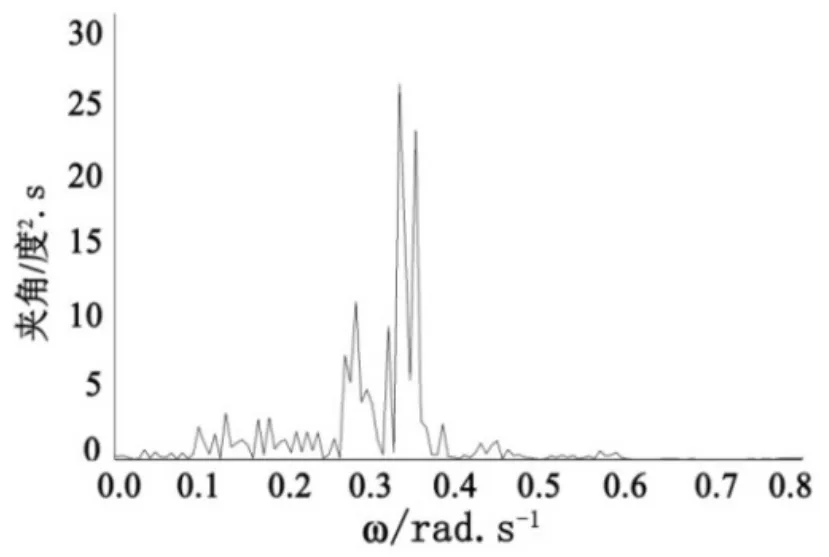
图13 波高5 m随机波横摇运动频谱

其中ω表示圆频率。船舶横摇固有频率为0.26 rad/s。在各波高下的运动的主频中都出现了接近固有频率的主频。此频率在能量方面对于水面航行体的横向摇摆运动的影响随着具有随机性质的波浪的波幅增大而减小。同时，从功率谱图可以看出水面航行体的横向摇摆运动具有多个复杂的频率，这些复杂的频率来自于随机性质的波浪中占能量的比例相对较大的正余弦函数的频率。然而还有一些偏离了随机波浪中的正余弦函数的频率，这些值来自于船舶运动中的多种不确定性，如航行体和波的不规则性、耦合影响和仿真中数值不稳定性。

4.2 随机运动结果的统计分布拟合和三维概率分析

由于船舶复原力不能用一个解析的表达式去相对准确的模拟出来，所以这些不规则的频率是无法通过一个完整的解析表达出来的，因此对于其随机波横摇运动的判定就需要通过数值的模拟。以下将通过随机统计的方法对航行体的横向摇摆运动性质进行概率分析。每次计算选取谐波的零时刻的相位的随机种子个数为10，相位是由计算机随机产生的。对各个波高下的船舶横摇运动都进行多组计算，得到不同初始相位下的运动计算结果。提取各横摇时历运动的幅值，统计其绝对值的直方图。下面使用左端点接近于0的log-logistics分布对在航行在具有随机性的波浪的航行体的横向摇摆运动的角度进行数值拟合。如式（10）：

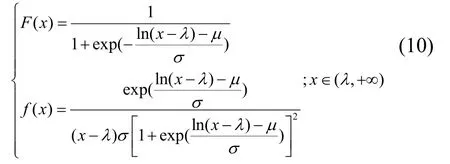
其中：μ表示位置参数（location），相当于分布的均值；σ表示尺度参数（scale），相当于分布的标准差；λ表示阈值参数(threshold)，表示分布的左极限。在研究中均取接近于0为其左极限。

每个波高下的统计结果和分布拟合，作出其百分比（percent）和角度（angel）关系如图14～图17。

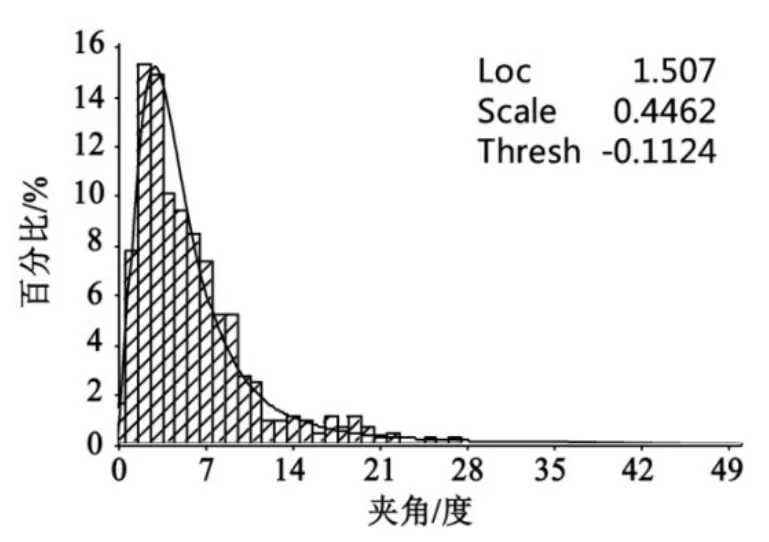
图14 波高2.5 m统计拟合分布

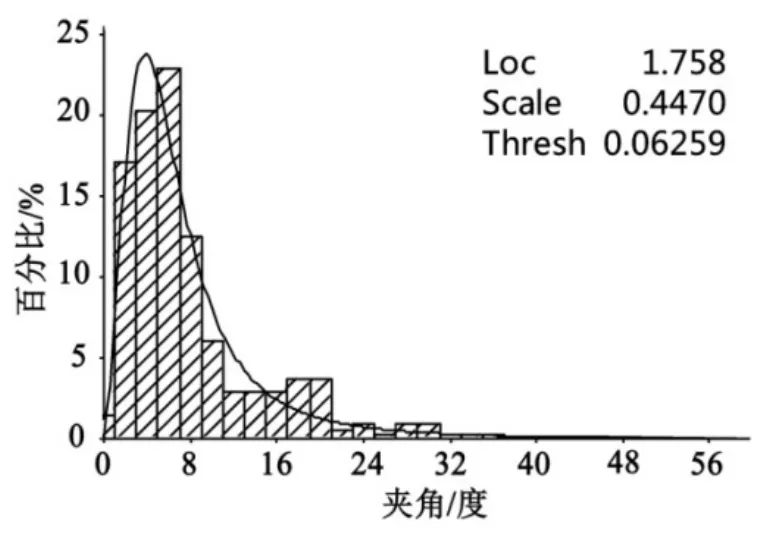
图15 波高3.5 m统计拟合分布

图16 波高4 m统计拟合分布

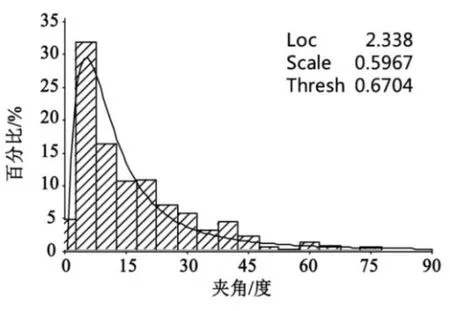
图17 波高5 m统计拟合分布

其中，loc表示参数μ，scale表示参数σ，thresh表示参数λ。

这样一组统计拟合分布图可以用来预测相应波高下的船舶横摇某个角度的发生概率。从统计拟合分布图中可以看出，其概率密度函数的集中区域随着随机波的波高增大而右移。这表明随波高增大，出现大角度横摇角的概率越来越大，并存在一定概率达到极限横摇角而发生倾覆。从图中亦可发现，在小波高情况下，船舶很难发生大幅横摇，在40°左右概率密度就接近于0了。在实际工程中船舶存在一个入水角，故概率分析考虑了此入水角为概率的吸收壁，即到达此角度时横摇角幅值将停留于危险状态不再回去。所以这就需要求得某个角度下的发生概率即求其分布函数。利用(10)式求图14～图17中的拟合结果的分布函数，并作出其概率（probability）和角度（angle）的分布函数，如图18。

图18 各波高分布函数示意

从图18可以看到在等角度的情况下，水面航行体的横向摇摆概率与具有随机性质的波浪的能量是正相关的。对于概率密度函数的参数继续进行拟合。根据仿真计算结果和理论推导，可用下面的式子对概率密度函数的均值进行近似表达：

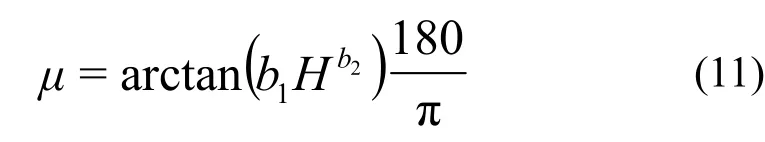
其中bi表示拟合的参数。这组参数与航行体的结构特性相关，若这组参数被确定，则航行体在随机复杂环境中的运动的概率性规律就可以准确描述，甚至（11）式的形式并不唯一，亦可通过大量的仿真数据对其进行训练从而进行调整。而这组参数是可以通过机器学习进行不断的训练而得的，从而能够达到准确预测水面航行体在不确定环境下的运动规律；H是随机波浪的波高有义值。引入机器训练的概念是另一个计算机科学和神经网络科学与水面航行体运动预测相结合的一个重要的研究方向，本文还是侧重于航行体在具有随机性质的波浪中的运动的分析方法框架和理论模型的建立，不在于参数训练原则和方法，因此不作赘述。对参数做出简易的训练处理，可得：b1=0.013928;b2= 0 .660010。结合参数训练结果做出概率分布函数的三维视图如图19。

图19 波高、横摇角三维分布函数

图19是基于统计概率学的模型对描述水面航行体的运动的概率公式进行参数分析而得到的解果，这个结果的价值在于可以对水面航行体在具有随机性质的环境中的运动进行概率预测。同时，引入概率学模型和计算机科学机器学习的思路对于宏观公式中的参数进行训练从而达到描述和预测海洋港口工程项目中的对象的运动规律的思路，是一个跨学科理论体系的建立，对于后续的海洋港口中的科学系统研究可以起到很好的指导作用。

5 结 语

1）基于瞬时转换矩阵考虑坐标轴的瞬变性建立了多自由度耦合非线性运动方程。考虑控制航向，对运动方程进行退化。基于势流理论推导波浪力的计算方法，并通过编程实现考虑瞬时位置的波浪力的实时计算。对于随机波利用无理数倍数关系划分波浪谱。最终实现对船舶在随机纵浪中的多自由度耦合下的参数横摇的研究。

2）研究船舶在随机波中的参数横摇运动发现，船舶在随机波中的参数横摇总是不稳定的混沌运动。其分叉区域在不断扩大。在某些情况下船舶横摇最大幅值不一定随随机波的波高增大而增大，但其能量大致是随波高增大的。

3）影响船舶在随机波中的参数横摇运动的主要频率来自于船舶的固有横摇频率和由二阶耦合项产生的频率。同时伴随着由船表面不规则性和波浪的随机性引起的其它一些无规律的频率，这些频率最终导致船舶参数横摇运动产生了不稳定性和混沌性。

4）通过统计和分布模拟对船舶在某个特定波长下的随机波中的横摇角发生的概率分布进行拟合和分析。并且以波高为自变量对其进行继续拟合，最终得到波高、横摇角下三维概率分布。发现这个三维分布曲面是随波高增大而向下滑移的，这符合了在大波高情况下大横摇角发生的概率更大。首次引入三参数 log-logistics分布进行拟合，其特性符合船舶在随机波中的参数横摇时角度发生的概率分布。通过这种分布模拟出的三维分布可以估算此波长下任意波高下的某个横摇角发生的概率。