智能电网短期负荷预测的研究

王 妍，王雪飞

（1.南京师范大学 电气与自动化工程学院，南京 210042；2.南京供电公司，南京 210019）

现代社会对电力的依赖程度越来越大，为了满足生产与生活对电力的不断需求，必然要求扩大电力系统的规模。但限于电能不能大量储存，电能的生产规模也不能无限扩大，因此负荷预测就显为重要，它对于电网安全稳定运行具有指标性意义，因为智能化电力企业的重要指标之一就是其电力负荷预测水平的高和低[1-7]。

精准的负荷预测是一个相当困难的课题，它容易受到很多因素的影响，尤其是不确定性的因素无法控制。假设将影响负荷的所有因素设为一个系统，那么这个系统就具有确定性和不确定性两个方面，是一个典型的灰色系统。根据上述，本文通过灰色模型理论提出了一种预测智能电网短期负荷办法，运用NGBM灰色模型用以提前预估测算智能电网中短期电力负荷，再运用PSO计算方法组合优化其参数，得出预测和实际运行曲线逐步靠近甚至重合的结果。

1 电力负荷的预测模型

1.1 预测模型的初步建立

GM(1,1)灰色预测模型，其模型最基本同时也是最简单的。建立该模型的理论依据是：众所周知，一阶微分方程式的曲线肯定具备数学指数函数方程式曲线的所有特点及其性质，这样就可以通过运用指数函数的拟合曲线进行对比，达到想要的预测的初衷[1]。但在实际过程中，社会用电负荷量是呈S型的曲线，GM(1,1)模型实际上根本没有可能得到较为精准的结论，虽然通过建立灰色Verhulst模型的方法在GM(1,1)的基础上确实可以分析S型增长曲线，提高预测的精准度[2]，但是也存在对那些平均增长率尤其过大的指数型增长，或者对Logistic增长趋势数据等进行预测时，存在误差过大的问题。因此，本文决定将非线性灰色Bernoulli模型（NGBM）引入到智能电网中短期电力负荷的预测中。

采用选用的基础数据开始搭建基础数据序列，并依据Bernoulli微分方程式建立如下模型：

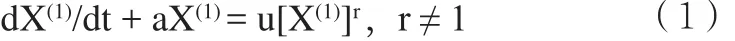
背景值z(1)(tk)的表达式为：

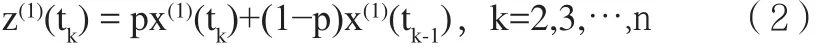
将式（1）两边同除以[X(1)]r得：

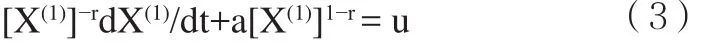
令q=[X(1)]1-r，则dq/dt=(1-r)[X(1)]-rdX(1)/dt，代入式（3）得：

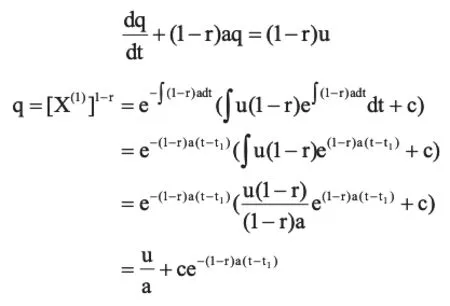
由于X(1)/(t1)=X(0)/(t1)，可知X(0)/(t1)(1-r)=u/a+c，得出预测值为：

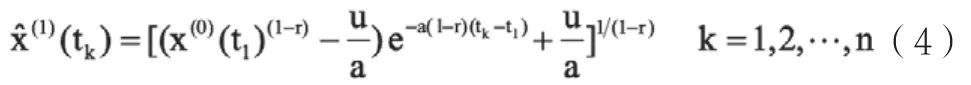
运用上述进行预测的数据值再进行累减计算就能得出真正预测值。

1.2 参数的组合优化

依据公式（3）即可得知：当参数r=0时，NGBM模型就是GM(1,1)模型；而当参数r=2时，NGBM模型演变成灰色Verhulst预测模型。从而可知，NGBM模型只是GM(1,1)模型和灰色Verhulst预测模型的基础化一般化的最初表现。通过不断调整不同数值的参数r，那么NGBM模型比普通GM(1,1)模型和灰色Verhulst预测模型有更为广阔适应特性。

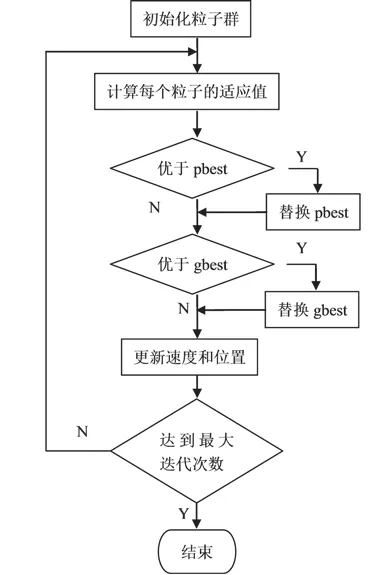
图1 PSO算法流程图Fig.1 PSO Algorithm flowchart

之所以建立灰色模型是为了大幅度提升预测的精度和准度，而为了保证这一目的必须要保证模拟的精准度才是最为重要的手段[3]。依据前述的分析演算可以知道，通过不断地对参数r和参数p筛选可以大大提高NGBM模型的预测精度，结合粒子群优化的良好性能，可以运用“粒子群优化算法”（PSO）通过演算和筛选，最终确定参数r与p的最优值，提高模拟的精准度。将参数r与p当作是决策中的变量，在不断地取值试验将参数r与参数p的择优最终演化为一个择优重组的问题。

运用“平均绝对百分误差”（MAPE）作为模拟预测精度的指标性的评价函数，假定优化选择的函数是：

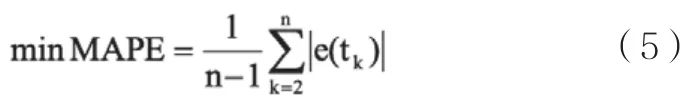
由图1可以直观地看出PSO的最初形态显示为一大群任意随机散布在解空间内的各种不确定位置游离粒子，可以运用迭代方法寻找最优解。实际上在无数次进行的迭代演变过程中，游离粒子受其最极端的2个数值影响不断兑变自身，结果是通过在整个空间搜索寻找得到的最优解，称之为全局的极值-gbest；另外，则是游离粒子通过自身寻觅得到的最佳位置，称之为个体极值-pbest。采用PSO算法，整个PSO算法过程详见图1。

2 负荷预测和分析

选用南京秦淮区区域2017年月用电量为例，通过建立的NGBM模型用对此预测，利用PSO算法对模型的参数r、p进行优选。假设通过PSO 算法后，实现 NGBM 模型参数求解的基本参数分别为：种群规模为40；最大迭代次数N=200；c1=c2=1.5。初始化的粒子群和搜索结束时的粒子群分布如图2所示。

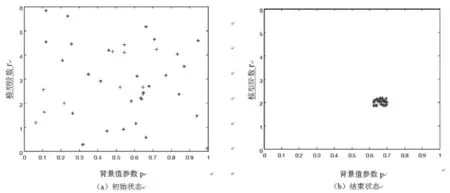
图2 粒子群状态Fig.2 Particle swarm status

从图2中可以看出，参数r的数值大多围绕在数字2周围，而参数p的数值基本上处于0.6～0.7之间，并倾向靠近0.7。因此，在预测该月的用电量时可以取r=2，p=0.66。在对秦淮区的12个月的用电量分别进行预测后，得到预测曲线如图3所示。由图3可见，预测用电量的变化轨迹与现实生活中用电量的变化轨迹近乎重合，无限靠近。

从图3中曲线轨迹分析，虽然之前预测的秦淮区域用电量变化曲线和现实生活中真正用电量的曲线轨迹无限靠近，但终究有误差，为了更进一步地优化模型的预测精准程度，需要利用参数来对其进行修正[5]。当取值数据离散范围足够大（即取值数据的灰色范围越广、程度越深），预测的精准度肯定也会越差。为满足预测的高精度需求，本文采用“马尔科夫链”方法来对灰色预测数据模型的残值差数来修正灰色模型的结果，修正后用电量的结果可以表示为：

其中，当k≤n-1时，

当k＞n-1时，

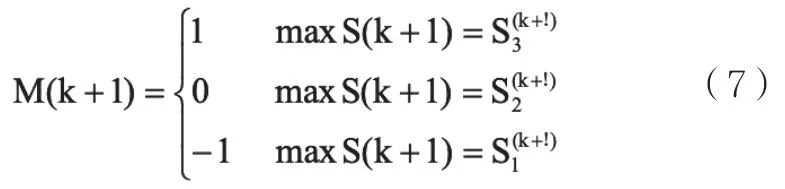
式中，Si(k+1)为马尔可夫链初始状态为k+1的概率。

用“马尔科夫链”方法来对灰色预测数据模型的残值差数来修正灰色模型预测结果，最后用得到的修正预测结论值与原先的预测结论值相加，即可得出实际的用电量预测结果，结果如图4所示。

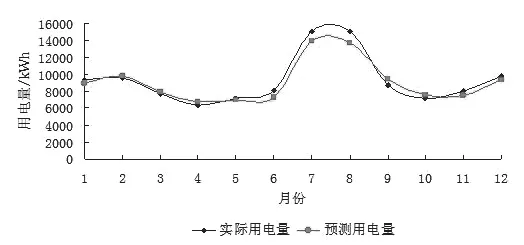
图3 秦淮区月用电量预测曲线Fig.3 Forecast curve of Qinhuai district monthly electricity consumption

图4 实际用电量与通过修正后预测用电量对比图Fig.4 Comparison chart of actual electricity consumption and predicted power consumption after correction

3 结论

基于灰色系统的理论研究方向，建立智能电网短期负荷预测模型，可实现智能电网中短期负荷预测。将负荷预测的关键性评价指标MAPE通过采用粒子群优化PSO计算方法，在模型中优选阶数r和参数p，将r与p分别作为决策中的变量使用，将模拟精度最高为终极目标任务，优化组合阶数r和参数p，释放粒子的不同速度，不断改变其速度惯性的不同权重求解其中的最优值，得出预测和实际运行曲线逐步靠近甚至重合的结果。实验结论数据恰好证明预测的结果符合最初建立该模型的初衷。为更加验证达到初时建立模型求得预测负荷值的准确度，再经过“马尔科夫过程”进一步修正预测的残值数差实际情况。将现实生活中的实际用电量和初时预测用电量的两条曲线进行比对，从而可以实现智能电网中短期负荷预测。