基于高精度差分法的线性常微分方程边值问题研究

2018-11-28陈铁军

安阳工学院学报 2018年6期

陈铁军

（益阳医学高等专科学校，湖南益阳 413001）

0 引言

常微分方程在科学和工程领域被广泛应用，随着生产实践快速发展，常微分方程逐渐演变成数学学科中联系实际最为重要的分支。常微分方程最基本问题是确定一个方程是否存在既定解，针对既定解的研究可分成三部分，分别初值问题、边值问题和特征值问题，很多偏微分方程既定解的问题不能使用解析形式进行表达[1]。因此，为了构造误差阶差分格式，利用参数样条函数代替未知函数，通过不同配置条件，引进迭代方法求解常微分方程边值问题。采用传统方法对边值问题进行研究，其计算结果都是不准确的，不能较好适应线性常微分方程，构造差分格式计算量相对较大。鉴于此，提出了基于高精度差分法的线性常微分方程边值问题研究[2]。利用差分法对微分方程边值问题进行研究时，其边界条件处理方式直接影响着差分解的精准度，针对处理过程中出现的差分解发散问题，使用边界近似方法不仅保证了差分解的收敛，还可使研究结果具有较高精准度。

1 线性常微分方程边值问题研究

1.1 线性常微分方程的边值问题

线性常微分方程是确定常微分方程是否存在既定解，通常给出一个常微分方程，当需要满足特定条件时，就会得到既定解[3]。针对线性常微分方程边值问题的研究，根据求解条件设置的不同，对边界问题相关导数在自变量上取值进行限定，即为边界条件。设线性常微分方程为：

最为常见的三种边界条件为：

将公式（1）与第一种边界条件组合在一起，构成第一边值问题；将公式（1）与第二种边界条件组合在一起，构成第二边值问题；将公式（1）与第三种边界条件组合在一起，构成第三边值问题[5]。

1.2 差分格式建立

高精度差分法是利用有限数量的离散点构成网格代替形式，具有连续性定解区域[6]。在有限个离散点中，使用离散函数近似代替具有定解属性区域内的连续变量函数，根据函数计算结果构成差分方程，该方程的边界问题解在各个节点上都被视为近似值，即为问题的数值解[7]。针对线性常微分方程边值问题研究，提出了高精度差分法，其使用原理为：通过离散方法，将常微分方程边值问题转化为各个离散函数数值所构成的线性方程，即为差分格式。一般情况下，要求线性方程组的系数矩阵是对角矩阵，差分格式阶段误差是判定差分格式数值解精准度标识之一，也为差分格式相容性[8]。

1.3 边界条件处理

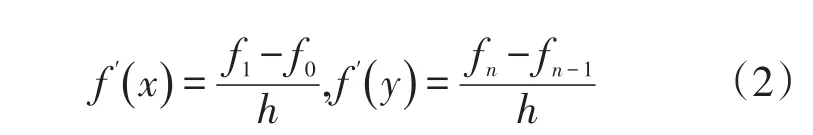
公式（2）中，h表示阶段误差，相比于微分方程的误差相对较低。

1.4 高精度差分法求解设计

高精度差分法是一种新兴的随机搜索算法，具有收敛速度快优势。由于需要求解的优化问题并不是一个简单变量问题，是由三种边界条件共同组成的[10]。因此，利用高精度差分法直接利用目标函数作为适应度函数，而具有变量属性的作为各个个体分量，虽然近似函数是具有多项式的，但是由于线性常微分方程边值问题比较麻烦，因此利用MAPLE符号计算目标函数表达式，进而提高整体求解效率[11]。

采用大正数K来将不同变量限制在[-K,K]以内，方便求解的快速进行，具体求解步骤如下所示：

1）数据初始化：初始化数据的规模，其中包括数据位置和速度。针对每个数据的研究都是在允许范围内进行的，其随机产生的数据具有初始位置和速度[12]。设随机产生的[-K,K]之间大正数为P，第n个数据的第z维初始位置为：

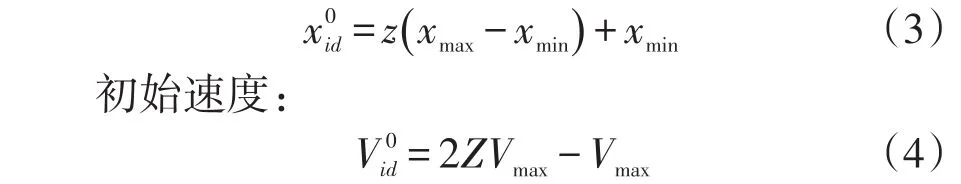
2）计算适应度值：针对不同边界条件，应按照构建的差分格式构造适应度函数，由于不同边界条件所对应的函数2n-2是一个变量，并且为最小化问题，因此可直接将该变量代入函数值之中，即为适应度值。

3）获取最好边界条件：针对每个边界条件，将其适应度值和经历过最好的最优值进行对比分析，进而选出目前最好边界条件的最优解。

4）差分算子：在搜索过程中，利用权重法对速度进行控制。此时的速度计算公式为：

公式（5）中：i表示进行第i次迭代；w表示最大迭代次数；d1,d2为随机数；表示搜索到第i次时最优位置；表示整体搜索到第i次时最优位置。根据上述公式对位置进行实时更新，并进化。

5）终止条件：设置最大迭代次数，当迭代次数达到最大值时，可结束进化。

根据上述设计结果，可得到线性常微分方程边值最优解，由此实现基于高精度差分法的线性常微分方程边值问题研究。

2 实验

针对基于高精度差分法线性常微分方程边值问题研究，设计实验进行验证分析。

2.1 实验参数设置

实验参数设置如表1所示。

表1 实验参数设置

2.2 实验结果与分析

根据上述实验参数，对实验内容进行对比分析。采用传统方法受到静态误差和动态误差影响，导致研究结果精准度较低，而采用高精度差分法对线性常微分方程边值问题进行研究，具有收敛速度快的优势，不会受到静态误差和动态误差影响，具有较高精准度。针对这两种方法在静态误差和动态误差条件下进行对比分析，结果如下所示。

2.2.1 静态误差

静态误差是线性常微分方程边值期望输出值与实际输出值的差值，如果静态误差较小，那么说明边值问题研究结果精准度就越高。以静态误差作为衡量方程边值问题的标准，将传统方法与高精度差分法研究结果精准度进行对比分析，结果如图1所示。

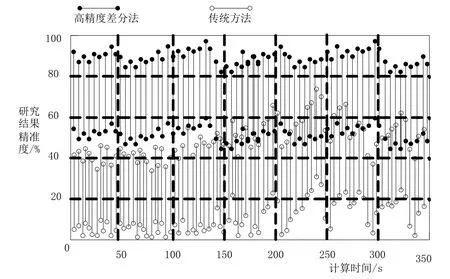
图1 两种方法静态误差研究结果精准度对比

根据图1所示对比结果可知：当计算时间为50s时，采用传统方法研究结果精准度最高为45%，而采用高精度差分法研究结果精准度最高为91%；当计算时间为100s时，采用传统方法研究结果精准度最高为43%，而采用高精度差分法研究结果精准度最高为90%；当计算时间为150s时，采用传统方法研究结果精准度最高为50%，而采用高精度差分法研究结果精准度最高为85%；当计算时间为200s时，采用传统方法研究结果精准度最高为49%，而采用高精度差分法研究结果精准度最高为90%；当计算时间为250s时，采用传统方法研究结果精准度最高为55%，而采用高精度差分法研究结果精准度最高为95%；当计算时间为300s时，采用传统方法研究结果精准度最高为50%，而采用高精度差分法研究结果精准度最高为98%；当计算时间为350s时，采用传统方法研究结果精准度最高为55%，而采用高精度差分法研究结果精准度最高为90%。由此可知，在静态误差下，采用高精度差分法对线性常微分方程边值问题研究结果精准度比传统方法研究结果精准度较高。

2.2.2 动态误差

动态误差是以研究线性常微分方程边值的时间变量为函数，提供研究相对稳定变化规律。如果动态误差较小，那么说明边值问题研究结果精准度就越高。以动态误差作为衡量方程边值问题的标准，将传统方法与高精度差分法研究结果精准度进行对比分析，结果如图2所示。

图2 两种方法动态误差研究结果精准度对比

根据图2所示对比结果可知：当计算时间为50s时，采用传统方法研究结果精准度为79%，而采用高精度差分法研究结果精准度为72%；当计算时间为100s时，采用传统方法研究结果精准度为75%，而采用高精度差分法研究结果精准度为74%；当计算时间为150s时，采用传统方法研究结果精准度为75%，而采用高精度差分法研究结果精准度为75%；当计算时间为200s时，采用传统方法研究结果精准度为73%，而采用高精度差分法研究结果精准度为77%；当计算时间为250s时，采用传统方法研究结果精准度为70%，而采用高精度差分法研究结果精准度为78%；当计算时间为300s时，采用传统方法研究结果精准度为69%，而采用高精度差分法研究结果精准度为72%；当计算时间为350s时，采用传统方法研究结果精准度为60%，而采用高精度差分法研究结果精准度为72%。由此可知，在动态误差下，采用高精度差分法对线性常微分方程边值问题研究结果精准度比传统方法研究结果精准度较高。

2.3 实验结论

根据上述实验内容，可得出实验结论：

①静态误差分析结果：当计算时间为50s时，采用高精度差分法比传统方法研究结果精准度高46%；当计算时间为100s时，采用高精度差分法比传统方法研究结果精准度高47%；当计算时间为150s时，采用高精度差分法比传统方法研究结果精准度高35%；当计算时间为200s时，采用高精度差分法比传统方法研究结果精准度高41%；；当计算时间为250s时，采用高精度差分法比传统方法研究结果精准度高40%；当计算时间为300s时，采用高精度差分法比传统方法研究结果精准度高48%；当计算时间为350s时，采用高精度差分法比传统方法研究结果精准度高35%。因此，在静态误差下，高精度差分法对线性常微分方程边值问题研究效果较好。

②动态误差分析结果：当计算时间为50s时，采用传统方法比高精度差分法研究结果精准度高7%；当计算时间为100s时，采用传统方法比高精度差分法研究结果精准度高1%；当计算时间为150s时，两种方法研究结果精准度一致；当计算时间为200s时，采用高精度差分法比传统方法研究结果精准度高4%；；当计算时间为250s时，采用高精度差分法比传统方法研究结果精准度高8%；当计算时间为300s时，采用高精度差分法比传统方法研究结果精准度高3%；当计算时间为350s时，采用高精度差分法比传统方法研究结果精准度高12%。因此，在动态误差下，高精度差分法对线性常微分方程边值问题研究效果较好。

综上所述，采用高精度差分法线性常微分方程边值问题研究是具有合理性的。