在数学建模教学中渗透核心素养

☉江苏省梅村高级中学 包正峰

一、问题的提出

《普通高中数学课程标准（2017年版）》一文在“课程基本理念”中创新性地指出：“高中数学课程以学生发展为本，以落实立德树人为根本任务，培育科学精神和创新意识，提升数学学科核心素养”.从而结合数学学科的基本特点，进一步归纳总结出了高中阶段数学的六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

数学建模作为高中阶段数学核心素养的一大主要内容，也是教师数学教学与学生数学学习过程中一大必备的技能技巧.数学建模是对具体的现实问题进行数学抽象，进一步用数学语言来表达问题，最后利用数学知识与相应的数学方法来构建出相应的数学模型，从而达到解决问题的目的.

在整个高中数学教学体系中，数学建模伴随前行，是概念教学与知识应用中的一条重要链条.那么如何在实际数学教学中培养与渗透数学建模思维呢？本文结合教学实践，通过具体的教学案例来剖析数学建模的渗透与培养.

二、问题的解决

数学建模是利用数学方法解决实际问题的一种实践，即通过抽象、简化、假设、引进变量等处理后，将实际问题用数学方式表达出来，进而建立起数学模型，然后运用先进的数学方法及计算机技术等进行求解.主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、求解结论、验证结果并改进模型、最终解决实际问题.

1.已有数学建模的完善

在很多数学问题中，题目已经给出了相应的数学表达式等相关条件，此时往往在已有的数学建模基础上进一步完善，通过题中对应的模型加以完善，寻找相应的破解思路，进而得以解决.

例1（2019届河南省高三一模）已知实数x，y满足3（x-1）≤ln（x+y-3）+ln（2x-y+2），则3y-5x=（ ）.

分析：利用题目中已有的函数、不等式模型，巧妙地构造函数模型f（t）=lnt-t+1（t＞0），并得到相应的对数不等式的结论：lnx≤x-1，进而结合该结论，利用两边夹定理，实现不等与相等的转化，再结合等号成立时的条件来处理.解析：构造函数（ft）=lnt-t+1（t＞0），由于，所以令f′（t）=0，解得t=1，函数（ft）在（0，1）上单调递增，在（1，+∞）上单调递减.

所以f（t）max=f（1）=0，即f（t）=lnt-t+1≤0，即有lnt≤t-1成立.

根据以上对数不等式的结论：lnx≤x-1，

可得ln（x+y-3）+ln（2x-y+2）≤（x+y-3-1）+（2x-y+2-1）=3x-3，

所以3（x-1）≤ln（x+y-3）+ln（2x-y+2）≤3x-3，

当且仅当x+y-3=2x-y+2=1时等号成立，解得x=1，y=3，此时3y-5x=4，

故选择答案：B.

点评：结合题目中已有的数学模型，即对应的对数式或指数式的特点，通过完善数学建模，得到对数不等式的结论lnx≤x-1或指数不等式的结论ex≥x+1，巧妙地转化其中的对数式或指数式，利用两边夹定理得以有效转化，进而利用等号成立时的条件加以巧妙转化，从而得以简单快捷地破解.

2.根据知识体系进行数学建模

借助题目所反映的知识体系，有针对性地进行数学建模，回归知识本源，进而借助于常见的思维方法来处理.比如在涉及平面向量的问题中，经常通过坐标系的建立，使其回归到坐标问题，进而借助坐标法来解决.

例2（2018届江苏省南京市高三第三次模拟考试·12） 在△ABC中，AB=3，AC=2，D为边BC上一点，若的值为______.

分析：根据题目所反映的知识，借助坐标系的数学建模——通过建立平面直角坐标系，设出点C（2cosα，2sinα），D（x，y），结合来确定x的值，再结合分别求出y的值，再来确定cosα的值，进而结合平面向量的数量积公式来求解的值.

解析：如图1，建立平面直角坐标系，则A（0，0），B（3，0）.

图1

设C（2cosα，2sinα），D（x，y），

又因为B，D，C三点共线，所以kBD=kBC，

故填答案：-3.

点评：在求解平面向量的相关问题中，利用数学建模，通过建立恰当的平面直角坐标系，将所涉及的平面向量坐标化，利用坐标运算来解答.这是解决平面向量问题的一类比较常见的思维方法，也是一种常见的思维方式.这样合理地利用知识体系来进行数学建模，可以使得问题的破解更加有效可行.

3.结合条件信息进行数学建模

在题目条件中，通过挖掘条件信息，包括问题背景、函数关系式、等式等，找出其中的内在规律，抓住问题的实质，通过形象思维的拓展，与对应的数学模型加以有机链接，从而建立起反映题目条件的数学模型，达到有效数学建模，然后运用数学模型所对应的数学知识和方法来分析与解决问题.

例3（2019届江苏省常州市武进区高三第一学期期中考试·14）若正实数x，y满足x2-xy+y2=9，且|x2-y2|＜9，则xy的取值范围为______.

分析：根据题目条件“正实数x，y满足x2-xy+y2=9”，通过变换得到32=x2+y2-2xycos60°，联想到解三角形中的余弦定理，借助形象思维进行数学建模，构造对应的三角形模型来直观处理.

解析：对于正实数x，y，根据x2-xy+y2=9，可得32=x2+y2-2xycos60°，

构造如图2所示的△ABC，其中BC=3，∠A=60°.

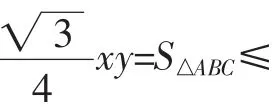
根据三角形的面积公式与三角形的性质可得（正三角形时面积最大，此时BC所对应的高最大，点A位于图中的A1位置），

可得xy≤9；

图2

由对称性不妨令x≥y＞0，则有|x2-y2|=x2-y2＜9，即x2＜y2+9，则△ABC为锐角三角形，

此时点A位于图中的临界点A2处，A2B⊥BC，则有x=，此时xy=6，

所以xy＞6.

综上所述，xy∈（6，9］.故填答案：（6，9］.

点评：借助题目条件，通过关系式进行形象思维，结合余弦定理来构造三角形模型，结合三角形的面积公式与直角三角形的性质来确定相应的代数式的取值范围.借助数学建模，通过直观模型角度的正常切入，使抽象思维转化为直观思维，结合数学模型的展示，达到了优化解题过程、节约解题时间、提升解题能力的目的.

三、感悟与反思

随着新课程理念的不断深入，数学建模在数学教学中的渗透与应用也越来越广泛，诸如函数与方程、不等式、统计与概率、数列、三角函数、解析几何、立体几何、排列与组合等众多的数学知识，都要求我们从数学建模的角度加以理解与掌握，从生活问题中加以切入数学应用.

其实，数学建模与其说是一门技术，不如说是一门艺术；技术大致有章可循，艺术则无法归纳成普遍适用的准则.学生只有通过不断地套用、模仿、修正、改进并创新，进而加深对数学知识的理解、对数学概念的掌握以及对数学模型的领会.通过数学建模，激发学生的求知热情与探究精神，领会数学思想，优化数学思维品质，提升数学核心素养.