基于卷积神经网络的调制识别新方法
2019-05-29张君毅赵国庆
王 鹏,张君毅,赵国庆
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.西安电子科技大学 电子工程学院,陕西 西安 710071)
0 引言
通信信号调制识别的主要任务是通过对截获到的通信信号样本进行信号分析和判别进而确定通信信号调制方式、调制采用的参数以及其他所需的信号参数,为进一步的通信信号处理分析提供依据,在频谱监测管理、通信侦察、电子对抗和无线电监测等领域具有广泛的应用。其中,调制方式作为区别不同体制通信信号的一个重要特征,对其进行识别是通信信号调制识别的一项基本任务,具有重要的研究意义。
针对通信信号调制方式识别的问题,国内外学者提出了大量的方法,实现了通信信号调制方式识别由早期的人工方式到基于机器学习的自动化识别的跨越式发展[1-7]。在实际实践中,现有基于机器学习的通信信号调制方式识别主要由数据预处理、特征提取、特征选择、分类器设计、模型训练和模型应用等步骤组成。然而,特征提取与选择需要非常强的专业知识背景和极高的技巧,并且需要根据训练结果进行多次调整,亟需更具普适性的替代方法[8-9]。针对这一问题,本文利用深度学习中的卷积神经网络实现特征的自动抽取和表达,并基于自学习的特征设计了分类器,实现了通信信号调制方式的识别,最后进行了仿真实验,仿真结果表明了该方法的有效性。
1 卷积神经网络
卷积神经网络(Convolutional Neural Networks,CNN)的研究经历了理论提出阶段、模型实现阶段以及广泛应用阶段[10-11],在图像分类[12]、语音识别[13-14]和文本处理[15-18]等领域取得了较好的应用效果,是当前学术界的关注焦点之一。经典的CNN结构如图1所示,包含了卷积层、池化层、全连接层和输出层等。其中,卷积层是利用卷积核提取特征,得到特征图;而池化层则是对特征图按照特定方式进行降采样处理,减小规模的同时保留有用信息,使得CNN具备抗畸变能力,提高网络的鲁棒性;全连接层一般位于网络尾端,对前面逐层变换和映射得到的特征进行回归分类等处理,实现输出。
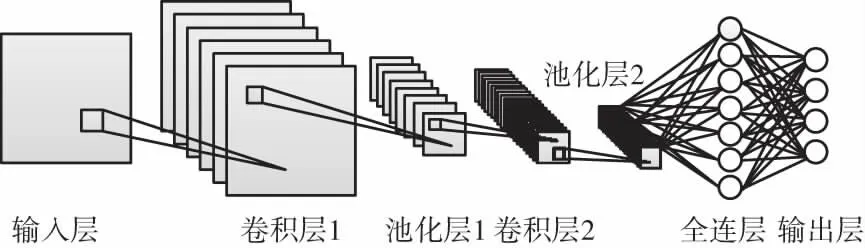
图1 CNN结构
2 基于CNN的调制方式识别新方法
为实现通信信号调制方式的识别,本文建立了如图2所示的CNN网络。可以发现,本文所建网络模型由1层输入层、2层卷积层、2层池化层、1层全连层和1层输出层组成。
本文所提模型的输入为IQ两路原始采样数据,卷积层对IQ两路数据进行卷积实现调制样式分类特征的自学习,池化层对自学习特征进行降采样提高分类特征的鲁棒性,最后将自学习的分类特征输入设计的分类器,输出当前特征对应调制样式的概率,最终实现调制样式的识别。可见,上述模型以原始采样数据为输入,避免了传统识别算法中特征的提取、选择与组合过程。
第1层卷积层的卷积核大小为1×5 ,特征图层数为64,激励函数为如式(1)所示的ReLu函数;第1层池化层的核大小为2×2,采用最大池化法;第2层卷积层的卷积核大小为1×5,特征图层数为32;第2层池化层的核大小为1×2,采用最大池化法;全连层的神经元个数为128,激励函数为如式(2)所示的Sigmoid函数;输出层采用Softmax回归多分类,代价函数采用交叉熵函数,如式(3)、式(5)所示。
ReLu函数:
f(x)=max(0,x)。
(1)
Sigmoid函数:
(2)
对于给定的训练集{(x1,y1),(x2,y2),...,(xm,ym)},yi∈{1,2,...,k},k表示分类的类别。对于给定测试输入数据xi,利用假设函数来对每一个类别估算出概率值p(yi=j|xi) ,得到如下输出向量:
(3)
式中,w表示模型的参数。为了更加清晰地述代价函数,首先定义一个示性函数,其取值规则如下:
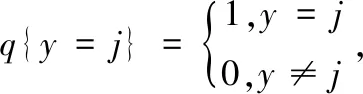
(4)
则代价函数可以表示为:
(5)
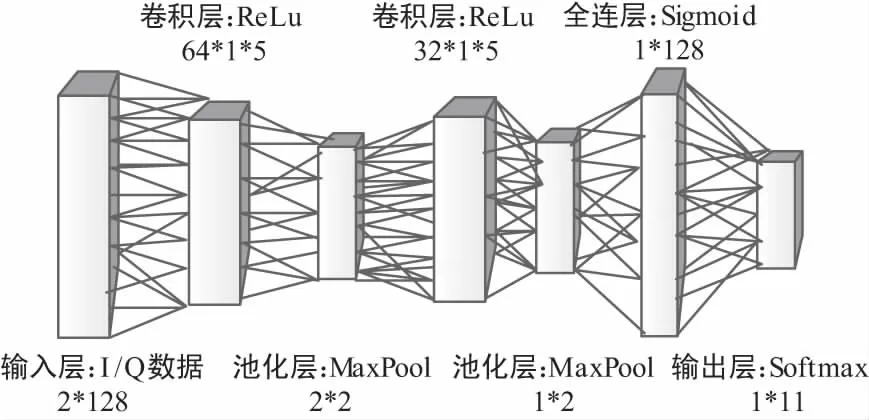
图2 用于调制方式识别的CNN网络结构
3 信号模型与数据样本
3.1 信号模型
调制后信号s(t)的复包络可以统一表示为:
s(t)=A(t)exp(jφ(t)),
(6)
式中,A(t)为信号的幅度;φ(t)为信号的相位,其具体方式由调制方式决定。式(6)给出了信号的解析形式,称其实部为同相分量,虚部为正交分量,如式(10)、式(11)所示:
sI(t)=Re{s(t)}=A(t)cos(φ(t)),
(7)
sQ(t)=Im{s(t)}=A(t)sin(φ(t))。
(8)
为了更好地描述真实世界中各种因素对信号的影响,本文采用如下所示的信号模型:
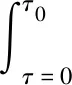
(9)
式中,n0(t)为由频率振荡器特性不一致而引起的载波变化;n1(t)为由时钟振荡器特性不一致而引起采样变化;h(t)表示时变的信道冲激响应;n(t)表示噪声。具体的信号产生方法详见文献[19],根据该方法产生的公开数据集详见www.deepsig.io/datasets。
3.2 数据样本
为实现算法性能的验证,本文采用文献[16]中所公开的数据集[13]作为样本数据。数据样本集包含3种模拟调制(WB-FM,AM-SSB,AM-DSB)和8种数字调制(BPSK,QPSK,8PSK,16QAM,64QAM,GFSK,CPFSK,PAM4)共11种调制方式的信号样本数据。其中,每种调制方式数据的信噪比范围均为-20~18 dB,信噪比步进为2 dB。在不同的信噪比条件下,每种调试方式的信号样本均由IQ两路组成,每路数据的采样点数为128,包含8~16个数字码元,每个码元的过采样率为8。在样本数据集中,所有调制方式信号的数据共162 060组;此外,样本数据集综合考虑了式(9)所示的多径衰落以及频率选择性衰落所引起的接收信号在幅度、频率、相位及时间延迟方面的影响,与真实环境中各类因素对通信信号传输的影响十分贴近。
4 仿真实验
为验证本文所提算法的有效性,利用3.2中所述的通信信号公开数据集对本文所提算法和文献[16]中的算法进行了仿真,并从计算复杂度和识别性能两方面进行了对比。其中,为提高算法的鲁棒性和计算效率,在本文所提算法及文献[16]算法的训练过程中均采用Mini-Batch方法,Batch的大小为1 024,即将所有的训练数据集以1 024个数据样本为单位进行随机组合,对一组数据进行训练后对模型参数进行更新,当整个数据集训练完成后称为1次训练。本文所提算法与文献[16]算法的训练次数都设定为100次。本文采用随机梯度法对所提算法中代价函数进行优化,并分析讨论了不同学习步长对算法性能的影响。为实现算法的性能验证,随机抽取数据集中70%的样本作为训练样本,并随机选择训练样本中的10%作为验证样本,剩余的30%作为测试样本。
4.1 计算复杂度
为体现本文所提算法在计算复杂度方面的优越性,本文首先从模型网络结构复杂度方面进行了理论分析。为实现调制样式的识别,文献[16]所提算法需完成2 830 427个模型参数的训练,而本文所提算法仅需完成143 275个模型参数的训练,模型参数训练量仅为前者的5.06%左右,极大地降低了网络结构的复杂度,可有效提高识别算法的计算效率。为进一步验证本文所提算法在计算复杂度方面的优越性,在配置为8G内存、i7处理器的计算机上对文献[16]算法和本文所提算法进行了仿真。仿真结果表明,文献[16]所提算法完成一次训练所需时间为410 s左右,而本文所提算法完成一次训练所需时间仅为30 s左右,是前者的7.31%,与前述理论分析结果基本一致。这就说明,相比文献[16]所提算法,本文算法可大幅提高调制样式的识别效率。
4.2 识别性能
图3给出了不同算法在不同信噪比条件下对不同调制方式的识别结果。其中,CNN1表示本文所提模型中随机梯度学习算法的学习步长为0.1,CNN2表示本文所提模型中随机梯度学习算法的学习步长为0.01。
从图3中结果可以看出,不同的学习步长对本文所提算法的识别效果具有一定的影响。总体来说,CNN2的调制识别效果比CNN1的调制识别效果略有提高(见图3(a)),在BPSK的识别上体现的尤为明显。
同时,从图3中可以看出,本文所提算法对不同调制方式的识别结果存在着较大的差异。具体来说,对11种调制方式中的AM-SSB、BPSK、GFSK、PAM4、16QAM、64QAM识别效果较好,在0 dB左右即可达到90%甚至接近100%的正确识别率;而对AM-DSB、8PSK、WBFM等调试方式的识别效果较差,在高信噪比条件下也只有70%左右的正确识别率,且算法性能不稳定。
此外,从图3中还可以看出,与文献[16]所提算法识别性能相比,本文算法除在8PSK、BPSK、CPFSK等调制方式的识别正确率上存在明显差异且互有高低外,在其它调制方式识别上基本相当,对11种调制方式的平均正确识别率也基本相当。
因此,结合4.1节中算法计算复杂度的分析,本文所提算法在与文献[16]所提算法在保持识别性能相当的同时,大幅降低了算法的计算复杂度与运行时间,更加有利于基于深度学习的调制方式识别算法的工程化。
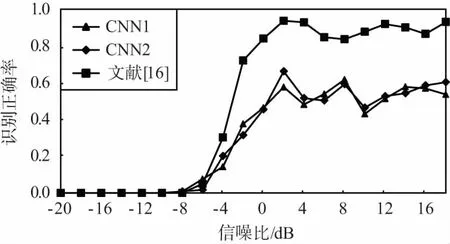
(a) 8PSK
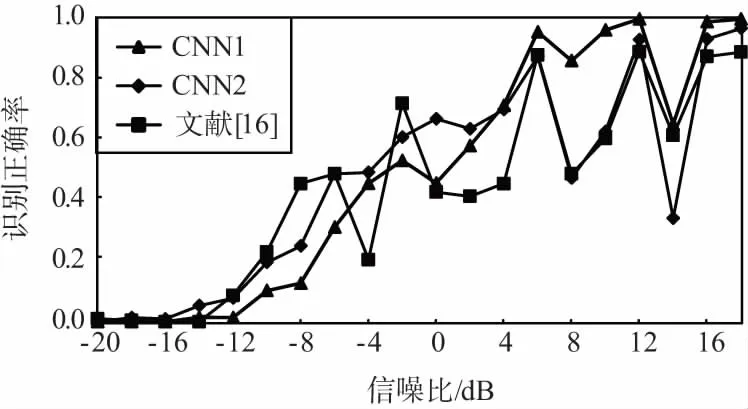
(b) AM-DSB
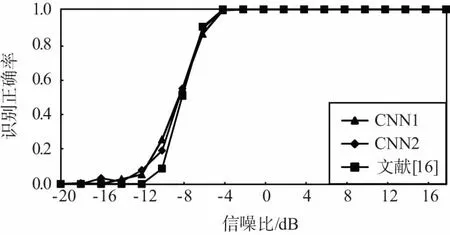
(c) AM-SSB
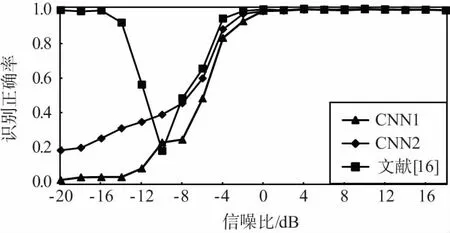
(d) BPSK
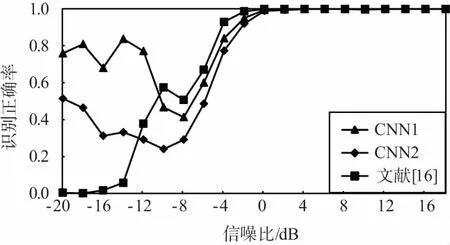
(e) CPFSK
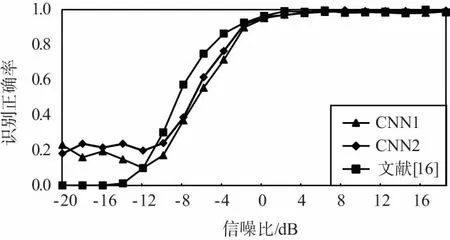
(f) GFSK
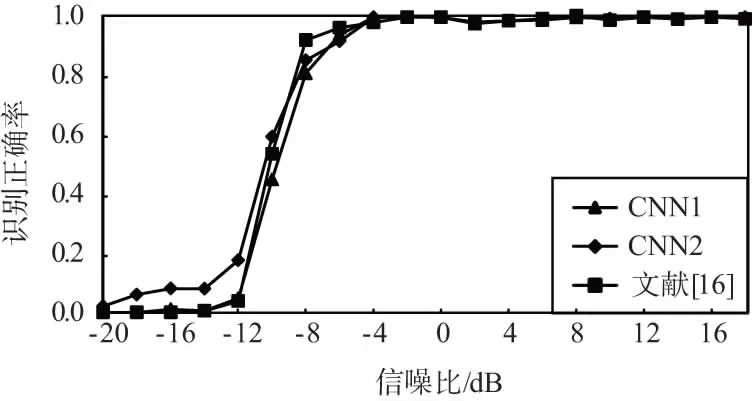
(g) PAM4
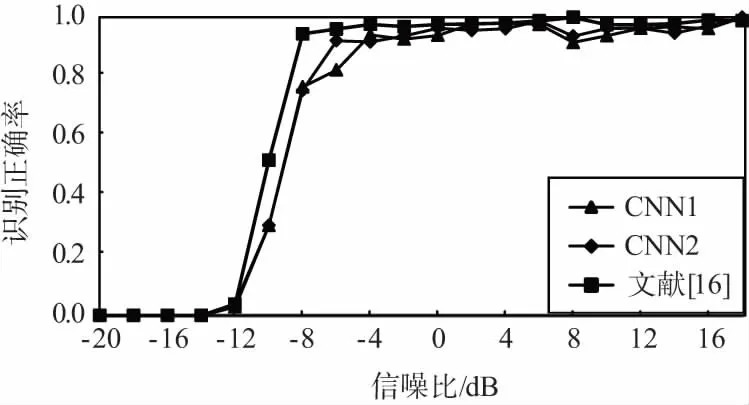
(h) 16QAM
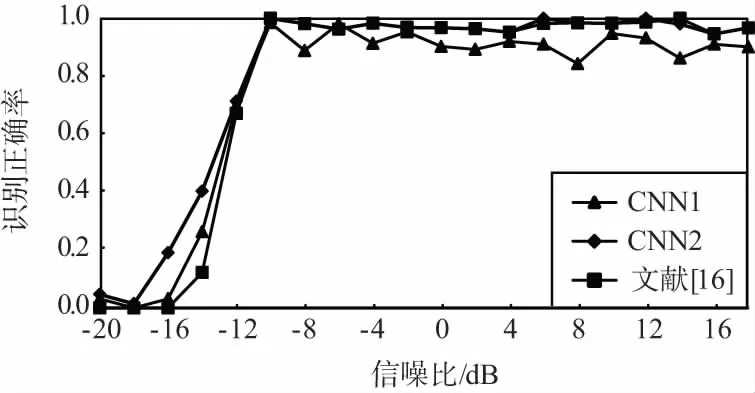
(i) 64QAM
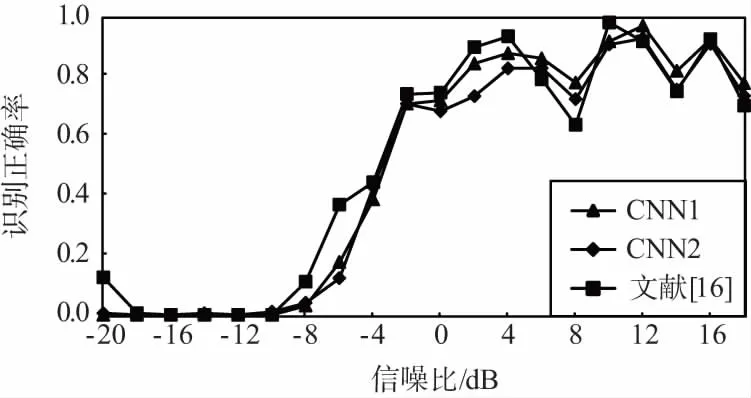
(j) QPSK
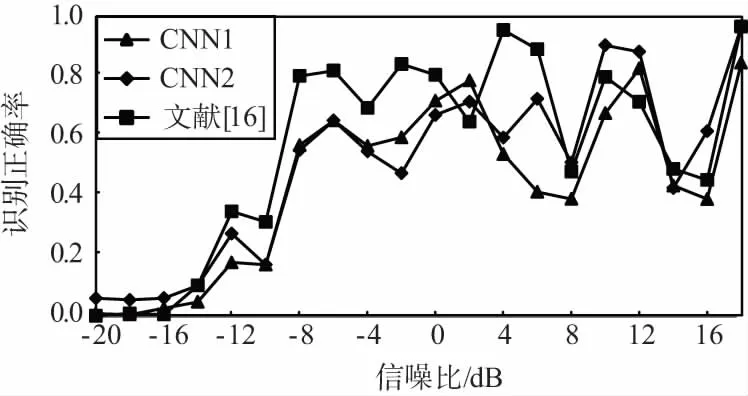
(k) WBFM
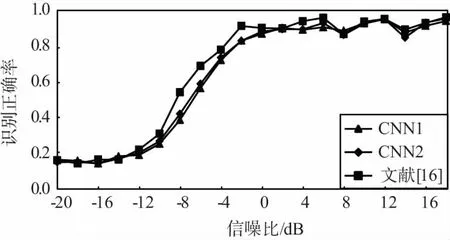
(l) 平均正确率
5 结束语
调制方式作为区别不同体制通信信号的一个重要特征,是通信信号调制识别的一项基本任务,具有重要的研究意义。为了避免传统算法中对特征的提取与选择问题,本文构建了一种基于卷积神经网络的调制方式模型,实现了分类特征的自学习与调制样式的识别。仿真结果表明了本文所提算法的有效性和可行性,同时也表明本文算法在性能稳定性、不同调制方式识别能力差异等方面尚存在一定的问题,这也是下一步工作的研究重点。
