三角函数题型例析

■杨 虎

三角函数是高考考查的重点，其主要考点有三角函数求值，三角函数的图像与性质，三角函数的应用等。下面举例分析。

题型1：三角函数的求值

例1已知sinα+2cosα=0，则2sinα·cosα-cos2α 的值是_________。

解：由sinα+2cosα=0，可得sinα=-2cosα，即tanα=-2。

故 2sinαcosα -cos2α =-1。

评析：三角函数的求值、化简、证明问题是高考的常考点，同学们要加以重视。

题型2：三角函数的图像与性质

例2函数f（x）=sin（ωx+φ）的部分图像如图1所示，则f（x）的单调递减区间为（ ）。

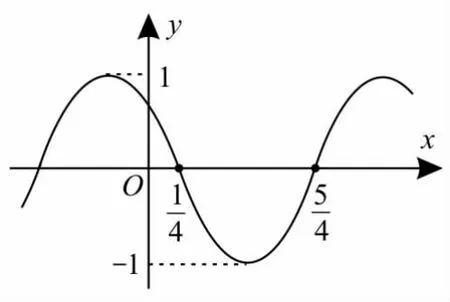
图1

解：由题意得即T=2。由可得ω=π，这时f（x）=sin（πx+ φ ）。 因 为所 以可得于是可得函数又因为f（0）＞0，所以f（x）=

评析：本题是一道识图题，通过对函数图像的分析，求其解析式，再研究函数的性质，这也是高考的常考题型。

题型3：三角函数的实际应用

例3某实验室一天的温度（单位：℃）随时间（单位：h）的变化近似满足函数关系：

（1）求实验室这一天的最大温差。

（2）若要求实验室温度不高于11℃，则在哪段时间实验室需要降温？

解：（1）由 题 意 可 得 f （t）=10-故当t=2时，当t=14时-1。

于是f（t）在[0，24）上取得最大值为12，取得最小值为8。故实验室这一天最高温度为12℃，最低温度为8℃，最大温差为4℃。

（2）依题意可知，当f（t）＞11时实验室需要降温。由（1）可得＞11，即又0≤t＜24，所以即10＜t＜18。故在10时至18时实验室需要降温。

评析：本题主要考查三角函数的性质在实际生活中的应用。对于第（2）问，发现f（t）＞11是解题的关键。