导弹姿态控制系统弹性振动抑制问题研究*
2019-05-28宿常鹏王雪梅李骏霄王兴龙
宿常鹏,王雪梅,许 哲,李骏霄,王兴龙
(1 火箭军工程大学,西安 710025;2 火箭军士官学校,山东青州 262500)
0 引言
导弹飞行过程中,弹体在各种载荷作用下不可避免地产生弹性振动。现行导弹的长细比一般较大,其弹性振动频率与控制系统频带接近。因此,导弹姿态控制系统的设计必须要考虑弹性振动对其稳定性的影响,并对其加以抑制[1]。目前,弹性振动抑制方法主要有两类:一是设计具有鲁棒性的控制器;二是采用陷波滤波器对振动模态进行抑制[2]。工程中广泛应用固定参数的陷波滤波器进行弹性振动抑制[3],尽管其具有一定的陷波宽度,但由于弹性振动频率变化范围大而效果并不理想。因此,孟中杰、闫杰[4]提出了自适应陷波滤波器的方法。该方法通过在线辨识弹性振动频率并据此调整陷波滤波器的参数,以实现弹性振动抑制。但是由于自适应陷波滤波器复杂度高、计算量大,弹上计算机难以应用[5]。
针对现有方法的不足,文中提出了时变陷波滤波器的方法。该方法简单易行,充分利用地面试验所得弹性模态数据进行陷波滤波器设计。理论计算和仿真实验表明:该方法弹性振动抑制效果好,适于弹上计算机使用,可以满足实时控制的需求。
1 姿态控制系统的模型
导弹是一个极为复杂的系统,需要对导弹的模型进行简化。首先,由于导弹在实际干扰作用下将在理想运动附近产生小扰动运动,可以将导弹运动微分方程简化为小扰动运动方程[6]。其次,忽略导弹俯仰、偏航、滚动3个通道的交链作用,将导弹姿态控制系统视为3个相互独立的通道。
对线性化的小扰动运动方程取拉氏变换可以得到弹体的传递函数,由于导弹的轴对称性,其俯仰和偏航通道的模型结构相同。把弹体俯仰(偏航)扰动运动作为受控对象,等效舵偏角Δδφ(Δδψ)作为控制输入,俯仰角Δφ(Δψ)作为输出量时,俯仰(偏航)通道刚性弹体的传递函数为:
(1)
式中:b1、b2、b3、c1、c2、c3为俯仰(偏航)通道刚性弹体的动力系数。
把弹体滚动扰动运动作为受控对象,等效舵偏角Δδγ作为控制输入,滚动角Δγ作为输出量时,滚动通道刚性弹体的传递函数为
(2)
式中:d1、d3为滚动通道刚性弹体的动力系数。
舵机伺服回路传递函数为:
(3)
由于导弹是时变系统,要保证系统在飞行过程中稳定,选取若干有代表性的时刻作为特征秒,在各个特征秒处认为系统是时不变系统,从而分析系统的稳定性。当攻角α=3°时,上述动力系数在部分特征秒处的计算结果见表1。
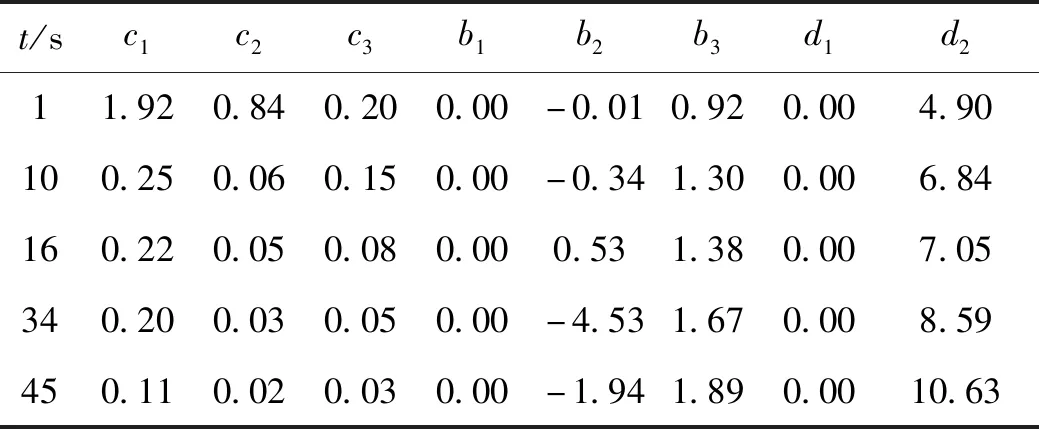
表1 动力系数计算结果
2 弹性振动分析
2.1 弹性振动模型
导弹弹体的弹性振动包括:纵向振动、横向弯曲振动和扭转振动。由于对稳定性影响最大的是横向(俯仰方向和偏航方向)振动,故仅研究弹体的弹性振动对俯仰(偏航)通道稳定性的影响。
弹性弹体的数学模型可以看作是在刚性弹体模型的基础上并联若干条支路,其路数与弹性振动主振型阶次相同[7]。由于高频振动通常可以忽略,文中仅考虑到3阶振型,故只需在刚性弹体的基础上并联3条支路。各阶弹性振型的传递函数为:
(4)
式中:ωi为第i阶主振型的固有频率;εi为第i阶主振型的阻尼;d3i为第i阶主振型的控制力弹性气动系数;wi为陀螺安装处第i阶主振型的斜率。
2.2 弹性振动抑制方法
为有效克服各种干扰,需要在设计中保证系统具备足够的稳定裕度,一般幅值裕度不得小于6~10 dB,同时要合理选择系统的带宽[8]。一般来说,系统的剪切频率低,离弹性振型的频率远,易于进行稳定性设计,但系统的姿态角偏差大,快速性差;系统的剪切频率高,系统的快速性好,静态误差小,但不利于弹性弹体的稳定性设计。综合考虑各种因素的影响,系统的剪切频率选在2~10 rad/s范围内。
由于弹体二阶以上弹性振型的振动频率远大于系统的带宽,对系统的稳定性影响很小,所以改进措施主要针对增加一阶弹性振动频率附近系统的稳定裕度展开。控制系统设计中最常用的方法是在控制回路中添加陷波滤波器[9],即通过加入以一阶弹性振动频率为中心频率的陷波滤波器,迅速衰减一阶弹性振动频率信号,从而消除弹体一阶弹性振动的干扰,提高姿态控制系统的稳定裕度。
3 控制规律设计
3.1 陷波滤波器设计
由于模拟-数字滤波器转换法简单易行,文中采用该方法进行陷波滤波器的设计。陷波器设计的基本原理是陷波器的零点与系统高频极点对消,其作用带宽为陷波器极点与零点之间的距离[10]。假定滤波器增益为1,陷波滤波器的传递函数可表示为:
(5)
设计陷波滤波器时应使陷波滤波器的时间常数接近1/ω1(其中ω1为弹体一阶弹性振动频率),阻尼接近弹性振动阻尼,由此确定传递函数的分子。确定陷波器传递函数的分母时要保证滤波器凹陷部分有足够的宽度和深度,同时还要考虑不能在系统低频相位上引起太大滞后。
考虑到弹体一阶弹性振动频率随飞行时间的变化范围为ω1=83~107 rad/s,故陷波滤波器的参数是时变的,即在各个特征秒处设计对应的陷波滤波器。以俯仰(偏航)通道为例,由表1可知,34 s时弹体静不安定力矩系数b2最大,此时对应的一阶弹性振动频率ω1=93.0 rad/s,一阶阻尼比ε1=0.069。设置陷波深度为-25 dB,得到34 s加入的陷波滤波器参数为ωi=93.0 rad/s,ζ1=0.069,ωj=63.2 rad/s,ζ2=1.0,对应的传递函数为:
(6)
其频率特性曲线如图1所示。

图1 陷波滤波器频率特性曲线
采用双线性离散变换,得到数字陷波滤波器的系统函数为:
(7)
式中:A0=0.46;A1=-0.69;A2=0.46;B1=-1.06;B2=0.28。A0、A1、A2、B1、B2在其他特征秒处的取值见表2。
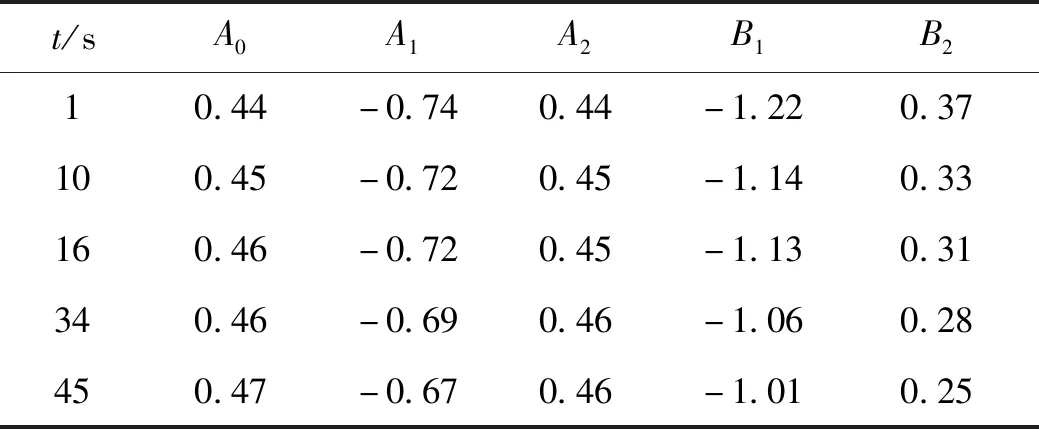
表2 时变陷波滤波器参数取值
3.2 校正网络选择
依据弹性弹体的数学模型,俯仰(偏航)通道加入时变陷波滤波器和校正网络的原理如图2。
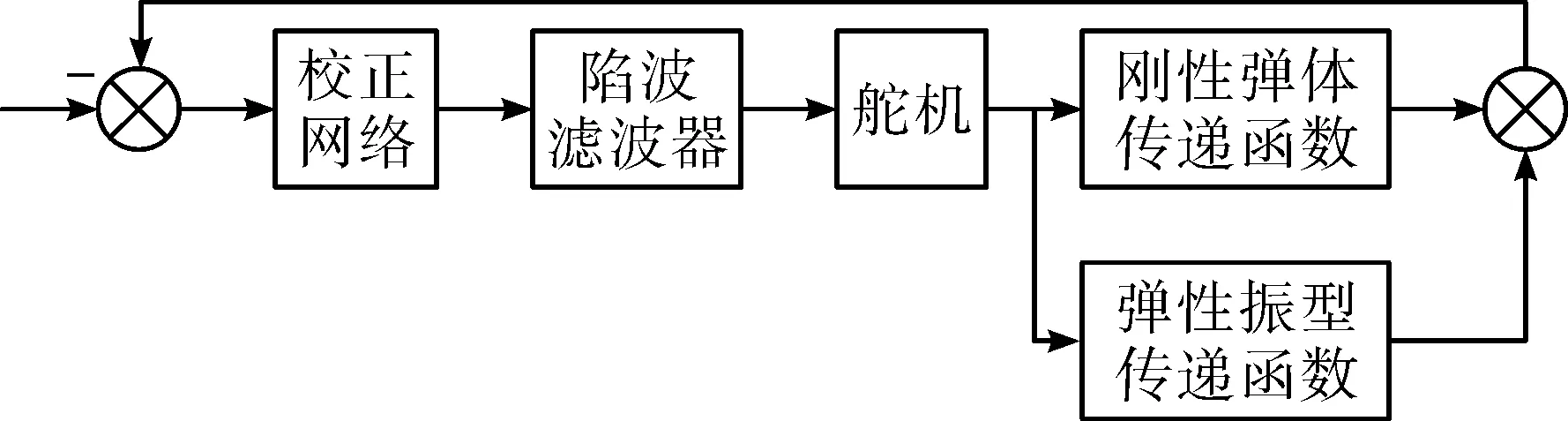
图2 控制原理图
校正网络的设计要综合考虑系统的稳定裕度、弹性振动和静态误差等因素。由于引入陷波滤波器会使系统在低频段产生相位滞后,为补偿低频的动态响应,通常在低频段采用超前校正[11],故俯仰(偏航)通道加入如下校正控制规律:
(8)
其频率特性曲线如图3所示。
按采样周期T=0.01 s,通过双线性离散变换,得到俯仰(偏航)通道数字校正网络为:
(9)
式中:A′0=118.2;A′1=-239.1;A′2=121.7;B′1=-1.5;B′2=0.6。

图3 校正网络频率特性曲线
滚动通道数字校正网络为:
(10)
式中:E0=114.9;E1=-128.3;E2=-134.8;E3=108.4;F1=-1.4;F2=0.8;F3=-0.2。
3.3 静态放大系数分配
为易于软件实现,各通道的校正网络采用变静态放大系数、不变网络结构的方法,则俯仰(偏航)通道静态放大系数为:
(11)
滚动通道静态放大系数为:
(12)
其中:
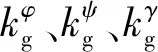
4 仿真实验与分析
4.1 数学仿真实验
考虑到系统参数变化和外界干扰的影响,将姿态控制系统中刚性弹体的传递函数设置为上限状态、额定状态和下限状态,3种状态的组合方式是从稳定裕度的大小来考虑的,上限组合使弹体传递函数幅频特性比额定状态上移、截止频率右移,下限状态使幅频特性下移、截止频率左移。3种状态的组成分别为:
1)上限状态:b2×0.9,b3×1.1,d3×1.1;
2)额定状态:b2×1.0,b3×1.0,d3×1.0;
3)下限状态:b2×1.1,b3×0.9,d3×0.9。
以34 s处为例,由表1可得俯仰(偏航)通道刚性弹体在3种状态下的频率特性曲线如图4。

图4 刚性弹体频率特性曲线
类似地,对弹性振动振型传递函数的参数设置为阻尼比不变,频率点下拉2 Hz、频率点不拉偏和频率点上拉2 Hz 3种状态。由于仅研究弹体的弹性振动对俯仰(偏航)通道稳定性的影响,故弹性振动振型传递函数的3种状态仅在俯仰(偏航)通道中讨论。通过求加入时变陷波滤波器后姿态控制系统在各个特征秒处的开环传递函数,确定系统的稳定裕度,进而判断系统稳定性。相关的符号说明为:
G为幅值裕度;ωcp为幅值裕度对应的剪切频率;P为相角裕度;ωc为相角裕度对应的剪切频率;Gtx,1为一阶振型幅值裕度;Ptx,1为一阶振型相角裕度。
滚动通道在3种状态下的稳定裕度范围如表3所示,可以看出:滚动通道在各种状态下的剪切频率为2.5~6.7 rad/s,幅值裕度大于16 dB,相角裕度大于48.0°,稳定品质良好。

表3 滚动通道稳定裕度范围
俯仰(偏航)通道在3种状态下的稳定裕度范围见表4~表6,可以看出:俯仰(偏航)通道在各种状态下的剪切频率在2.2~6.9 rad/s,幅值裕度大于7 dB,相角裕度大于34.0°,一阶振型幅值裕度大于6.6 dB,相角裕度大于34.4°,姿态控制系统稳定品质良好。

表4 额定状态稳定裕度范围

表5 下限状态稳定裕度范围
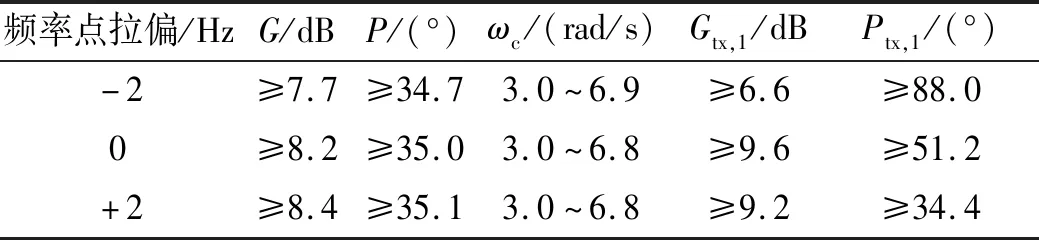
表6 上限状态稳定裕度范围
4.2 半实物仿真实验
设置姿态控制系统半实物仿真的条件如下:仿真步长取0.01 s,导弹的射程为500 km,初始姿态角为φ0=89.5°、ψ0=-0.5°、γ0=1°。舵效上拉偏状态为正10%,弹体力矩负10%;舵效下拉偏状态为负10%,弹体力矩正10%;仿真状态中加入空气舵干扰3倍,一阶阻尼比为0.069。
导弹在仿真过程中基本沿标准姿态角飞行,稳定过程中的姿态角速率小于5°/s,最大舵偏角小于20°,关机前的姿态角速率小于0.5°/s,满足技术指标要求。半实物仿真实验的部分状态和结果见表7。
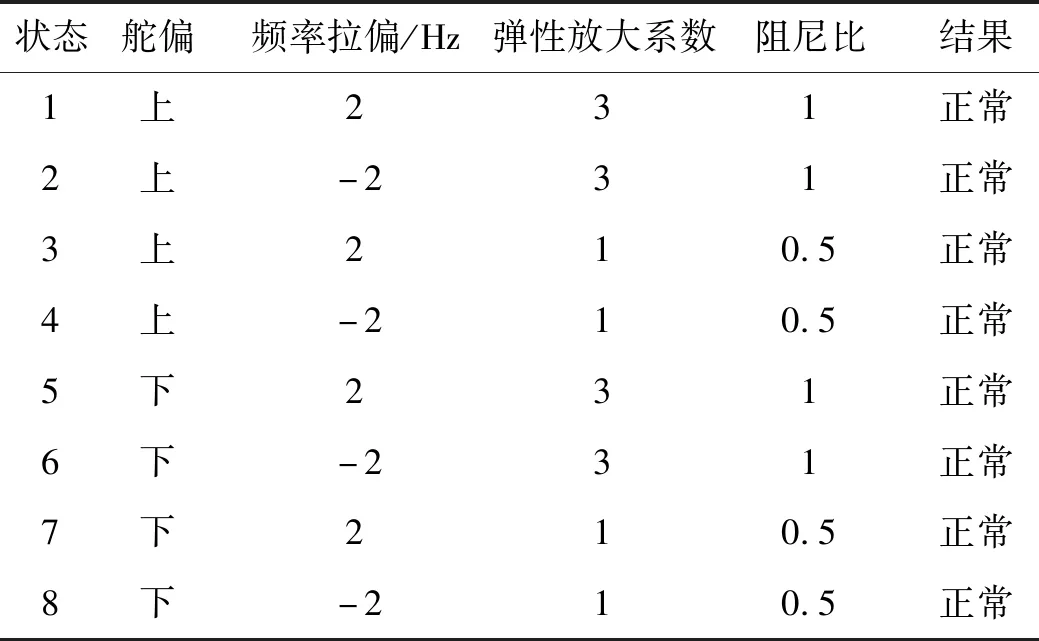
表7 半实物仿真状态及实验结果
5 结束语
文中提出了在导弹姿态控制系统中加入时变陷波滤波器的方法,以抑制弹体的弹性振动对系统稳定性的影响。以某型导弹为例完成了时变陷波滤波器的设计、校正网络的选择和静态放大系数的分配。理论计算和仿真实验表明,该方法有效抑制了弹体弹性振动的干扰,适于弹上计算机使用。
