代际利他主义者的跨期决策——基于人口结构变化的分析

黄志国 李秀芳 陈孝伟

一、引 言

随着多年来计划生育政策的实施和经济的持续发展以及医疗技术水平的不断提高，我国国民的平均预期寿命越来越长，由1981年的67.77岁到2015年的76.34岁，在 30余年间增长了近 10岁，而在可预见的未来，随着医疗水平的进一步提高和经济的持续增长，我国国民的平均预期寿命还将继续延长，我国已经开始进入老龄化社会。为应对老龄化问题，我国于2015年末开始实施全面二孩政策，以期通过提高生育率来解决老龄化问题。其实施一年有余，情况却不容乐观，根据卫计委的统计数据，2016年我国人口出生率为 12.95‰，同比仅上升 7.9%，全面二孩政策并没有带来生育率的明显上升。原因在于抚育子代的成本上升以及我国养老保障制度具有的独特特点。

随着经济的发展，抚育子代的成本也在上升，抚育子代最重要的成本是教育成本，教育可以形成人力资本，人力资本越多，未来产出越高，经济发展也越迅速。未来的产出越高，则子代的生活水平越高，父母的效用水平越高，把尽量多的收入用于对孩子的教育似乎看起来是一个明智的选择。而且，社会学的研究表明，我国国民是典型的代际利他主义者，对子代人力资本投资的动机植根于基因之中已延续了上千年。然而，一个典型的消费者首先需要是一个理性的人，以最大化自己的终身效用为目标。因此，即使具有代际利他主义倾向的消费者，也会在教育、消费与储蓄间做出权衡。

我国实行的是统账结合制的养老保障制度，该制度将代表性消费者的未来消费从两方面与未来的经济状态联系在一起：由于存在现收现付制的统筹账户，未来工资水平决定了老年人从年轻人那里得到转移支付的大小；而由于存在基金制的个人账户，未来的资本收益决定了代表性消费者的当期储蓄在未来获得的收益，而代表性消费者的消费、储蓄、教育决策决定了未来的工资和资本收益，因此代表性消费者的消费、储蓄、教育决策也决定了自己未来在老年期的消费。

本文旨在建立一个统账结合制养老保障下利他主义者的扩展 OLG模型，并引入古典主义的生产技术以及资本更新方程，结合规模报酬不变的人力资本积累方程，以探讨生育率上升和平均预期寿命延长对消费者当期消费、储蓄和教育投资行为及对未来工资、未来资本收益和人均产出的影响，从而为我国的教育和养老政策提供一个理论参考。

二、文献综述

黄少安和孙涛(2005)建立了具有东方文化信念的世代交叠模型，将遗赠、赠予和赡养等问题纳入决策框架分析了我国居民的消费和储蓄特征。刘庆彬和郝胜龙(2011)建立了双向世代转移模型分析我国家庭赡养和教育投资决策问题，分析认为存在社会保障的情况下，代表性消费者会增加对子女的教育投资，从而促进经济增长。汪伟(2012)通过构建一个统账结合制的三期世代交替模型讨论了代表性家庭的消费、储蓄和教育投资决策模式。汪伟和艾春荣(2015)构建了一个包含老龄人口寿命和负担效应的三期世代交叠模型，分析了我国人口老龄化和储蓄率的动态演化关系和储蓄率之间的地区差异，研究发现老龄人口负担上升并没有对储蓄产生负效应，但老年人的预防性动机对储蓄率产生明显的促进作用。杨继波和吴柏钧(2015)建立了一个三期世代交叠模型，从宏观角度分析了代表性消费者在子女教育投资和养老保险投资的最优决策，并进行了实证检验。 樑严成 (2016)建立了包含延迟退休的内生生育率OLG模型研究生育率和经济增长问题，研究发现无论采取何种养老保障制度，延迟退休都使生育率上升，而在内生增长模式下，生育率上升则会使经济增长放缓。

Barro和 Becker(1989)提出了一个广为沿用的利他主义函数以分析具有代际利他主义倾向的代表性消费者如何决策生育率和消费以及对经济的长期影响。Futagami和Nakajima(2001)从生命周期理论出发，通过建立引入公共养老系统的内生增长一般均衡模型分析人口老龄化对经济增长的影响，表明在延迟退休的政策选择下人口老龄化可以促进经济增长。Pecchenin和 Pollard(2002)通过建立存在教育税情况下的利他主义OLG模型以分析教育投资对社会福利的影响，认为提高教育税、降低社会保障税能够提高社会福利。Soares(2005)建立了一个利他主义者跨期消费和人力资本投资模型，分析了持续增长经济和 Malthusian经济中父代预期寿命延长和子代死亡率下降对父代消费、父代人力资本投资、子代人力资本投资以及生育率的影响。Prettner(2013)建立了内生生育率、内生教育投资、内生健康支出的跨期消费模型，分析认为生育率随抚养成本上升而下降，随利他倾向的上升而上升。Fanti和Gori(2014)建立了内生生育率和内生寿命的 OLG模型分析代表性消费者的储蓄和生育率决策以及经济的长期均衡，分析认为代表性消费者所面临的子代教育税和自身健康支出对生育率选择有负向影响。

总结已有文献，较少有学者在统账结合制的养老保障制度下讨论人口老龄化或生育率变化的影响，引入代际利他动机的文献也很有限，而多数文献在讨论生产部门时，都使用了或暗含了一个重要的假设：资本折旧率为百分之百。这种假设使得生产部门只能利用每期新增的投资进行生产，而无法使用往期折旧后的剩余，每期的资本也无法累积，割裂了代际之间在资本上存在的联系。本文在已有文献的基础上，在统账结合制的养老保障制度下，引入代际利他动机，考虑资本折旧的影响，讨论人口老龄化和生育率上升对代表性消费者的跨期储蓄、消费和教育投资决策以及对下期人均产出、工资和资本收益的影响。

三、理论模型

（一）模型假设

Lt为 t时期的年轻人，ηt=Lt/ Lt-1为 t-1期的生育率，代表性消费者在青年期确定性地生存至期末，而在老年期的生存概率为pt。政府实施现收现付制与基金制结合的养老保障制度：个人账户实行基金制管理，在青年期征收，若缴纳人在老年期仍生存，则返还给缴纳人，若缴纳人死亡则作为遗产平均分配给其子女；统筹账户实行现收现付制，对当期年轻人征收，用于支付当期老年人的养老金。消费者对影响决策的未来变量有合理的预期。

（二）利他主义代表性消费者

1. 效用函数

代表性消费者一生的效用由三部分构成：年轻时期的消费、老年时期的消费和对每个子女的教育投资。为t时期年轻人的消费，β为时间偏好因子，Etpt+1为t+1期的生存概率①，为t+1期的老年人消费，即t期进入t+1期的年轻人的消费。et为以教育投资衡量的每个子女的受教育程度。代表性消费者是一个利他主义者，可以从子女的受教育程度中获得效用，ζ为相对效用系数。

2. 约束条件

代表性消费者整个生命周期的总收入由三部分构成：年轻时期的工资收入、年轻时期由父辈死亡得到的遗产(由父辈未消费的储蓄和个人账户基金累积之和构成)、老年时期的养老保障。而支出由五部分构成：对子女的教育投资、年轻时期的消费、年轻时期的储蓄、年轻时期支付的养老保障税、老年时期的消费。

μt是当期工资中用以支付所有子女总教育投资的比例，st为t时期年轻人的消费；τt为统筹账户工资税比例，统筹账户实行现收现付制，即完全用来支付当期老年人的养老金的比例；σt为个人账户的工资税比例，个人账户为基金制，若在t+1期缴纳人仍生存则返回给缴纳人，若在 t+1期缴纳人死亡则作为遗产平均分配给其子女；rt为t时期的资本收益。式(3)表明年轻人的自主消费和储蓄由工资收入的剩余部分和分得的遗产构成。式(4)表明老年人的消费由总储蓄(自发储蓄与强制储蓄之和①个人账户的设立可以视为政府对年轻人的强制储蓄。)的t+1期预期价值加上t+1期统筹账户征收的工资税。

3. 最优解

在约束条件下对式(1)最大化，得到代表性消费者的最优决策框架：

（三）生产技术

代表性消费者对子女的教育投资可以在子女进入成年期后形成人力资本，人力资本可以提高生产效率，而资本积累主要由年轻人进行。人均人力资本的生产为 C-D函数形式，总人力资本为劳动人口与人均人力资本的乘积，资本存量的更新遵循古典主义更新过程，即由上期折旧后的剩余和本期新的投资构成，社会中的总储蓄由劳动人口——社会中的年轻人进行，老年人只消费而不工作也不储蓄。技术进步外生并以 g的速度增长。物质生产同样以C-D函数的形式进行。

（四）决策框架

将式(8)、式(9)、式(10)、式(11)、式(12)代入式(13)得到下期产出、下期人均产出、下期工资水平、下期资本收益和下期工资-资本收益比：

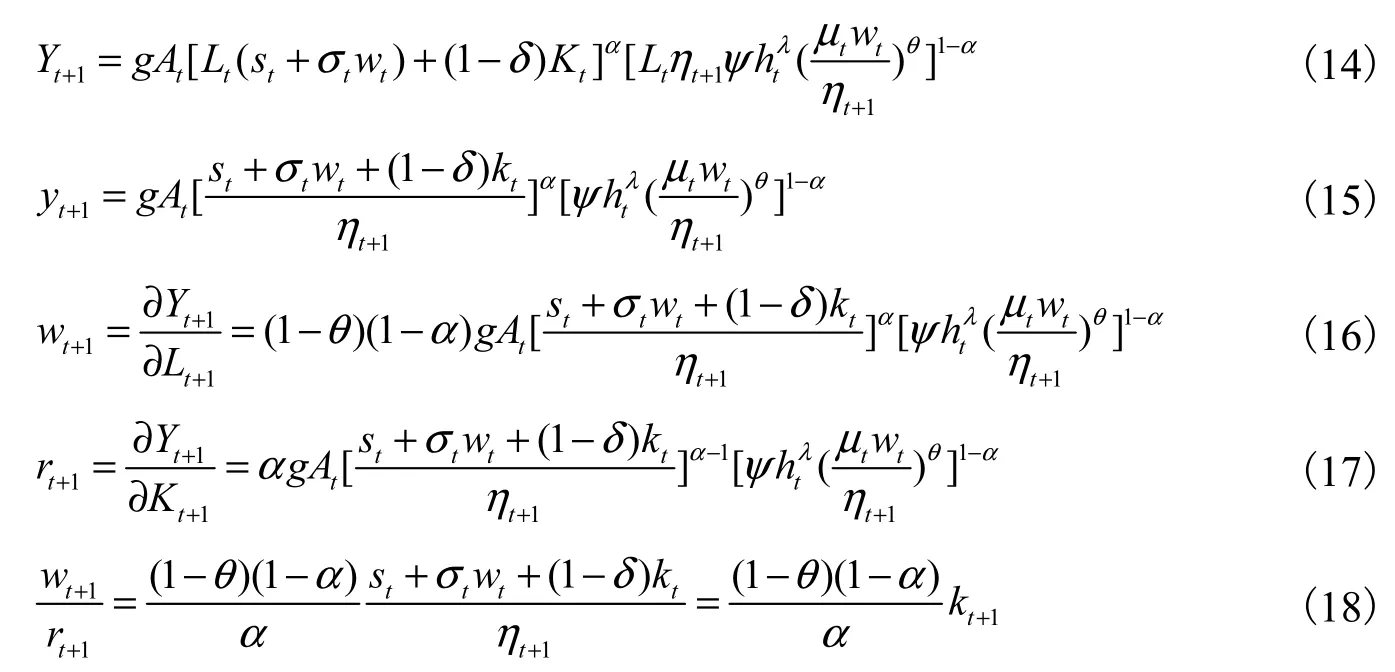
将式(5)、式(6)代入式(18)，解得下期工资-资本收益比为：

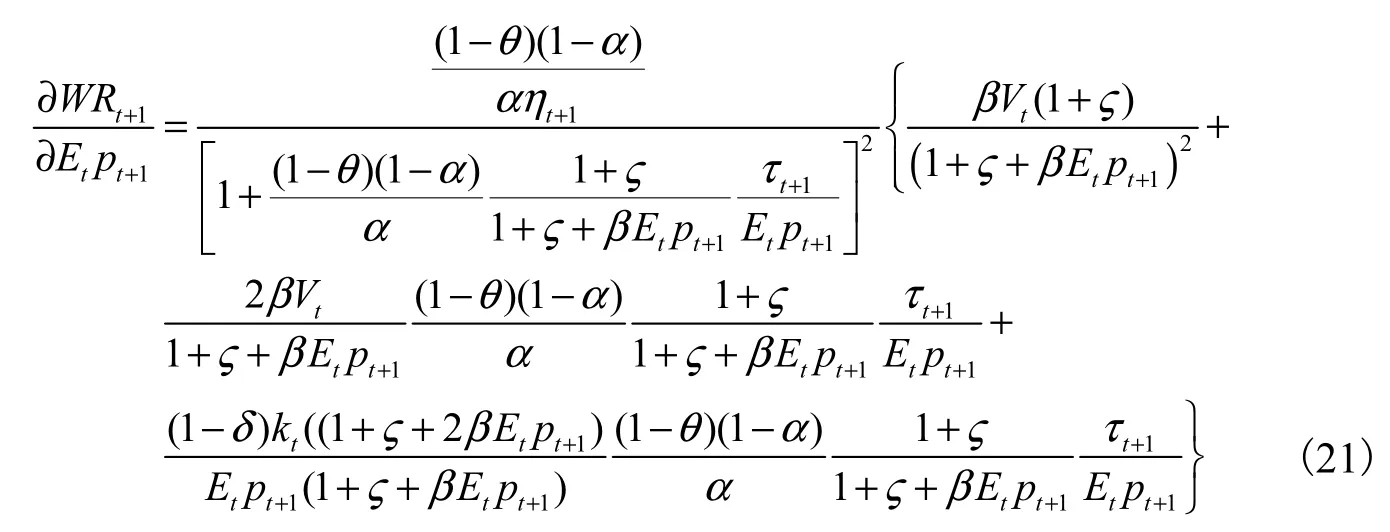
命题1：生育率上升不会影响当期消费者的储蓄行为，平均预期寿命延长会使当期消费者的储蓄上升。

命题2：生育率上升会使消费者的人均教育投资下降，平均预期寿命的延长也会使人均教育投资下降。

由式(6)可明显看出平均预期寿命和生育率对人均教育投资的影响为：

命题3：生育率上升不会影响消费者的当期消费，平均预期寿命延长会使消费者减少当期消费。

由式(7)可得到平均预期寿命和生育率对当期消费的影响为：

由于对数函数与原函数有相同的单调性，出于简化计算的考虑，以下分析生育率和平均预期寿命对下期资本收益、工资和人均产出的对数的影响。

命题4：生育率上升会使下期人均产出下降。

由式(15)可得到平均预期寿命和生育率对下期人均产出的影响为：

生育率的提高对下期人均产出的影响是显然的，但平均预期寿命的延长对下期人均产出的影响则取决于当期的经济结构状态。

命题5：生育率上升会使下期工资水平下降。

由式(16)可得到平均预期寿命和生育率对未来工资水平的影响为：

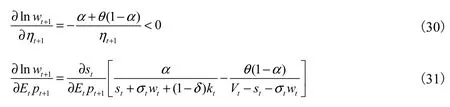
生育率的提高使下期工资下降，但平均预期寿命的延长对下期工资的影响则不那么明显。一方面二者之间的关系取决于系数的大小，另一方面社会中的人均资本存量也起着很重要的影响。

命题6：生育率上升会使下期资本收益上升，平均预期寿命的延长会使下期资本收益下降。

由式(17)可得到平均预期寿命和生育率对未来资本收益的影响为：

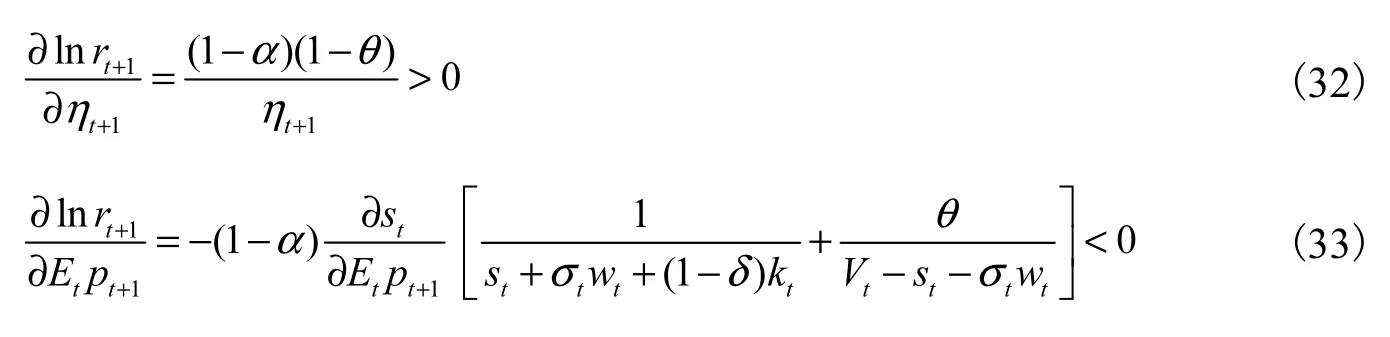
其原因在于：生育率上升使劳动供给增加，其他条件不变，资本将因而变得相对稀缺，从而资本收益上升。平均预期寿命延长将使储蓄增加，从而资本供给增加，需求不变，则资本收益下降。

生育率和平均预期寿命对年轻时期的消费、年轻时期的储蓄、对子女的教育投资、下期的资本收益的影响都是确定性的，但平均预期寿命对下期工资和下期人均产出的影响不那么确定。

四、参数校准

傅晓霞和吴利学(2006)计算出我国1978—2004年间的产出弹性为0.687，赵志耘等(2006)计算出我国 1978—2004年间的平均产出弹性为 0.56，辛永容等(2009)则测得在0.36～0.47之间。因此我们将α设为0.687、0.56和0.36。张军和章元(2003)使用了 5%的折旧率，李宾(2011)基于已有文献使用的折旧率在 5%～10%，万东华(2009)测算出的平均折旧率为7.3%。因此我们将年折旧率δ设为0.05、0.073和0.10。张军和章元(2003)推算的1952年价格的1978年资本存量为12361.96亿元，从而1978年现价的资本存量为 17637.73亿元，李治国和唐国兴(2003)推算出 1978年现价的资本存量为14112亿元，白重恩(2009)推算的1978年现价的资本存量为5067亿元。我们将资本存量Kt设为 5067亿元、14112亿元和 17637.73亿元①此设定的考虑是以36年作为1期，以下工资和储蓄的设定也都基于此。。Young(2003)计算出我国1978—1998的年 TFP增长率为 1.4%，杨汝岱(2015)估计出我国 1998—2009年间的TFP增长率为 3.83%，而人均产出年均实际产出增长率为 8.84%，故人均资本存量的年增长率为 6.36%，从而我们将人均资本存量kt设为 5480.69元、15265.01元和19078.83元，而将年技术进步率g设为1.025。蒋 云赟 和任若恩(2004)建议在评估养老金缺口等问题时采用 4%、6%的收益率，而经计算得到的年资本收益率为 10.25%，故设定年资本收益 rt= 1.04，1.06，1.10。Pecchenino 和 Pollard(2002)将ς设为 0.98，本文同时考虑两类特殊的利他效用系数1和βpt=0.12，从而设定ς=0.12，0.98，1。

以 1978年价格计算的我国人均储蓄最大值为7069.2元，最小值为340.33元，因此我们将 st-1、st分别设为340.33元、7069.2元。而人均工资最大值为9451.05元，最小值为 615.0元，因此我们将 wt-1、wt分别设为615.0元、9451.05元，1978年以来的平均生育率ηt为 0.164。郭凯明和龚六堂(2012)将时间偏好因子设为β= 0.9830≈ 0.55，本文以36年为 1期，故设β= 0.9836≈ 0.48，根据我国养老金制度的有关规定，设定τt=τt+1=0.12,σt=σt+1=0.08。汪伟(2012)将年轻人进入老年期的概率pt设为 0.76，θ设为0.628，本文遵循此设定。

由于数据量庞大而不能一一列示，为尽可能说明问题，以下将参数依数值大小分为高、中、低三组。根据《中国统计年鉴(2016)》以及各省的统计资料，我国的生育率为1.05②此数据是由统计年鉴公布的1%人口抽样调查数据计算而来的。，最低为北京0.707，最高为广西1.79；而根据联合国人口基金《世界人口状况报告(2016)》世界的平均生育率水平为 2.5，亚太地区为 2.1，发达国家为 1.7，发展中国家为 2.6，最不发达国家为 4.0，中国为 1.6，最低为葡萄牙等国 1.2，最高为尼日尔7.9。考虑我国的实际情况，采用 0.7、1.6和 2.6分别作为低、中和高三级生育率水平。此外，根据《中国统计年鉴(2016)》，中国人的平均预期寿命为76.34，而根据《世界人口状况报告(2016)》，发达国家平均预期寿命为79，发展中国家约为70，最不发达国家约为64.5，世界平均水平约为71.5，限于数据的可得性，本文将0.5(＝64.5/120)作为预期生存概率的下限，采用汪伟(2012)的0.7作为中间水平，采用0.9作为上限。

表1 可变参数设定

表2 固定参数设定

由图1可以看出，0.5明显是对预期生存概率的低估，它使得各种系数组下的均衡储蓄为负。在低预期生存概率组下，5480元则明显是对当期资本的低估，它使得下期资本收益、下期工资、下期人均产出都被低估；而19080元则又是对当期资本存量的高估，它使得下期资本收益和人均产出被高估。

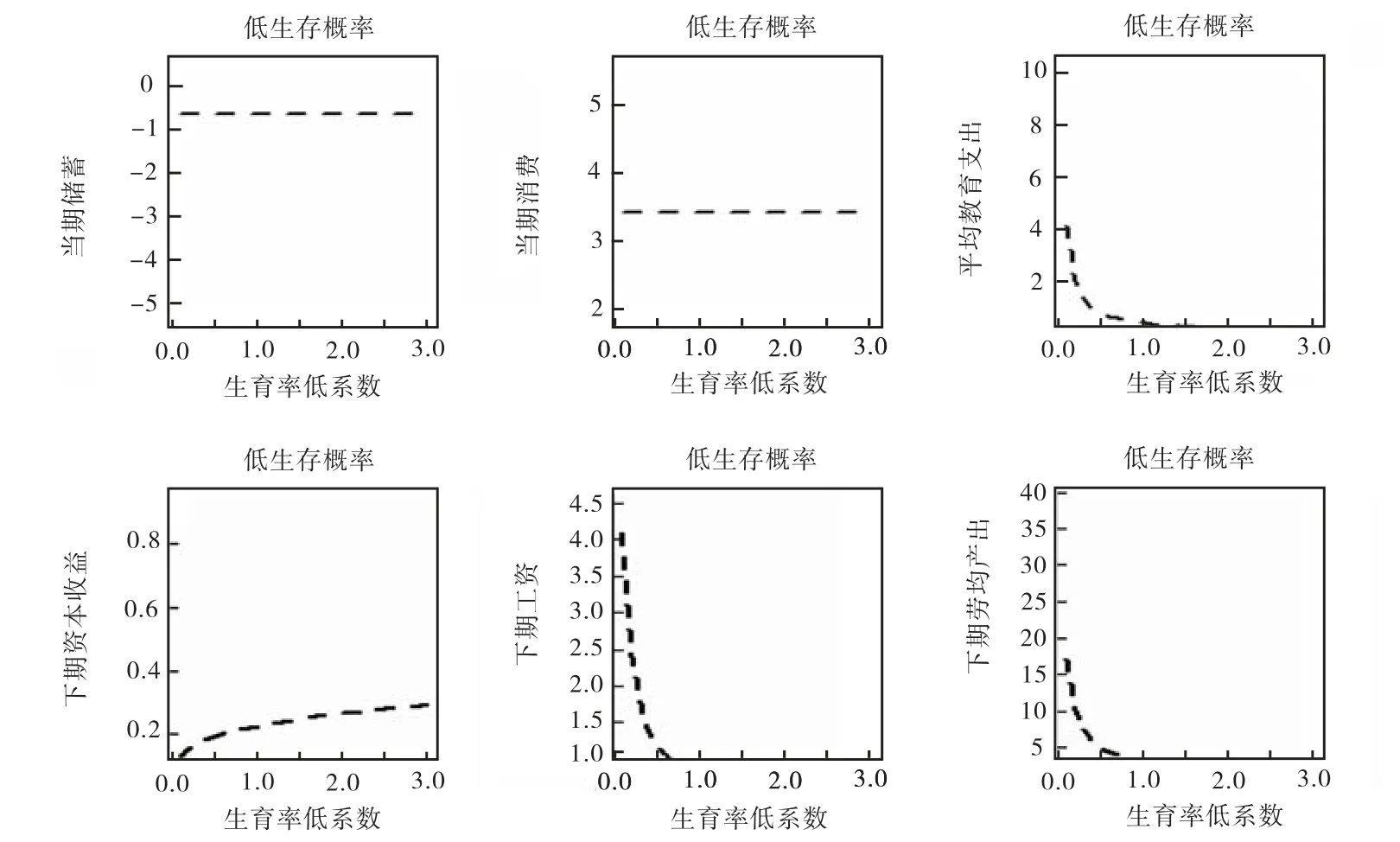
图1 低预期生存概率组

由图2可以看出，0.7仍然是对预期生存概率的相对合理估计，它使得高系数组下的均衡储蓄接近为正。而在中生存概率组下，高系数组则是对实际经济系统的相对合理估计，低系数组和中系数组下的经济系统使均衡的资本收益偏低。

图2 中预期生存概率组

由图3可看出，0.9是对预期生存概率的高估，它使各种系数组下的均衡储蓄几乎均为正，但在中系数组下为负。而在高预期生存概率组下，高系数组则是对实际经济系统的相对合理估计，低系数组和中系数组下的经济系统使均衡的资本收益偏低。

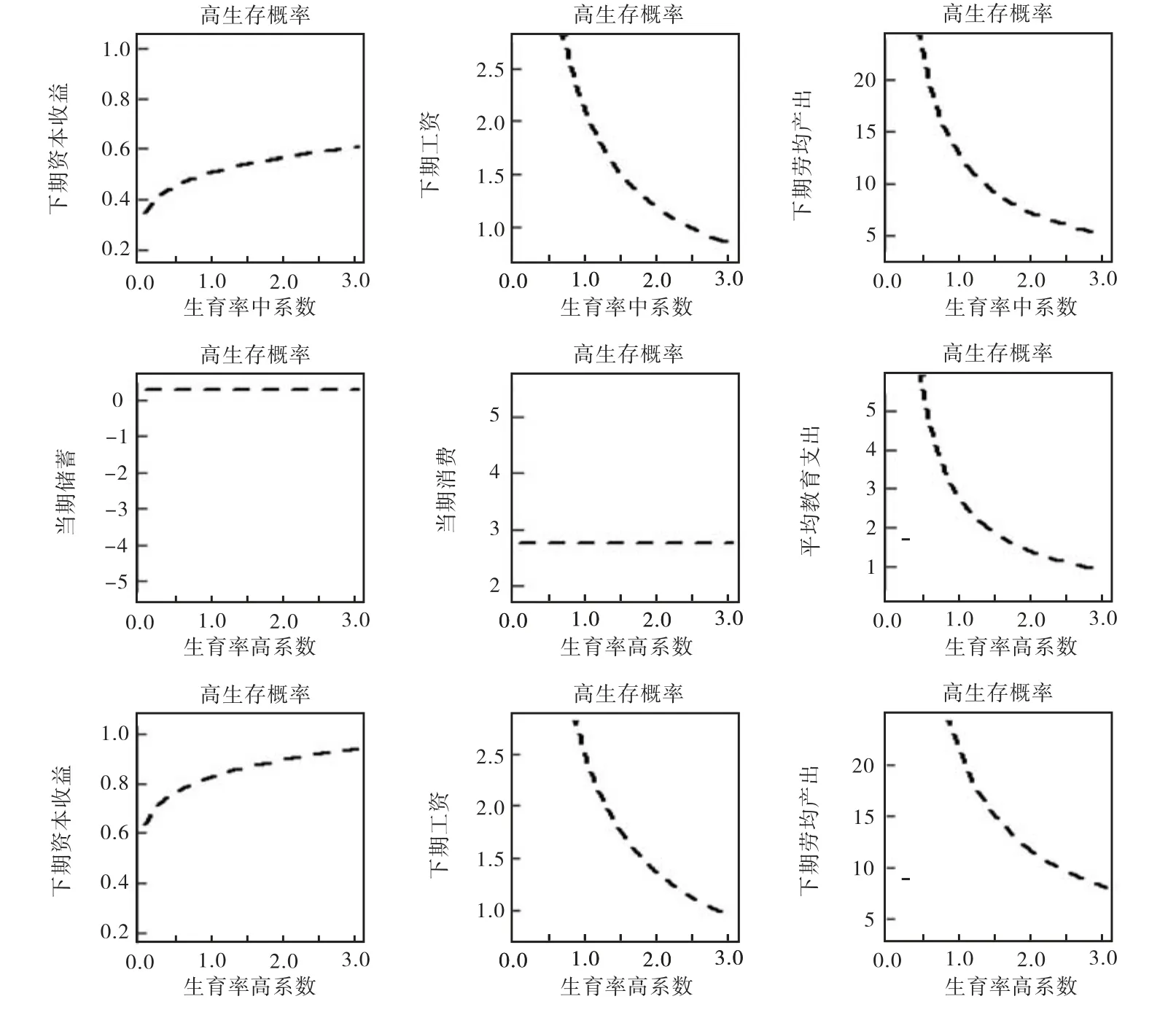
图3 高预期生存概率组

综合图1、图2和图3可以看出，在各种系数组下，当期消费、当期储蓄不随生育率的改变而改变，平均教育投资、下期工资和下期人均产出随生育率的提高而下降，下期资本收益则随生育率的提高而提高。从而我们可以看出，工资的生育率弹性绝对值要大于资本收益的生育率弹性。而越是处于高系数下，平均教育投资、下期资本收益、下期工资和下期人均产出越高，说明高系数组所代表的经济体系运行得更快。

由图4可以看出，从储蓄的角度，只有在高系数0.7下的生育率才可能是对实际生育率的合理估计，而只有在预期生存概率超过 0.8时，均衡的储蓄才为正。从资本收益的角度，0.7在任何系数组下都不是对生育率的合理估计，它使得均衡的下期资本收益偏低。

由图5可以看出，在1.6的生育率水平下，当预期生存概率超过0.8时，均衡储蓄在低、高系数组为正，在中系数组为负。而只有在高系数组下，1.6才是对生育率水平的相对合理估计，在低系数组和中系数组下，1.6的生育率水平使得均衡的下期资本收益过低。

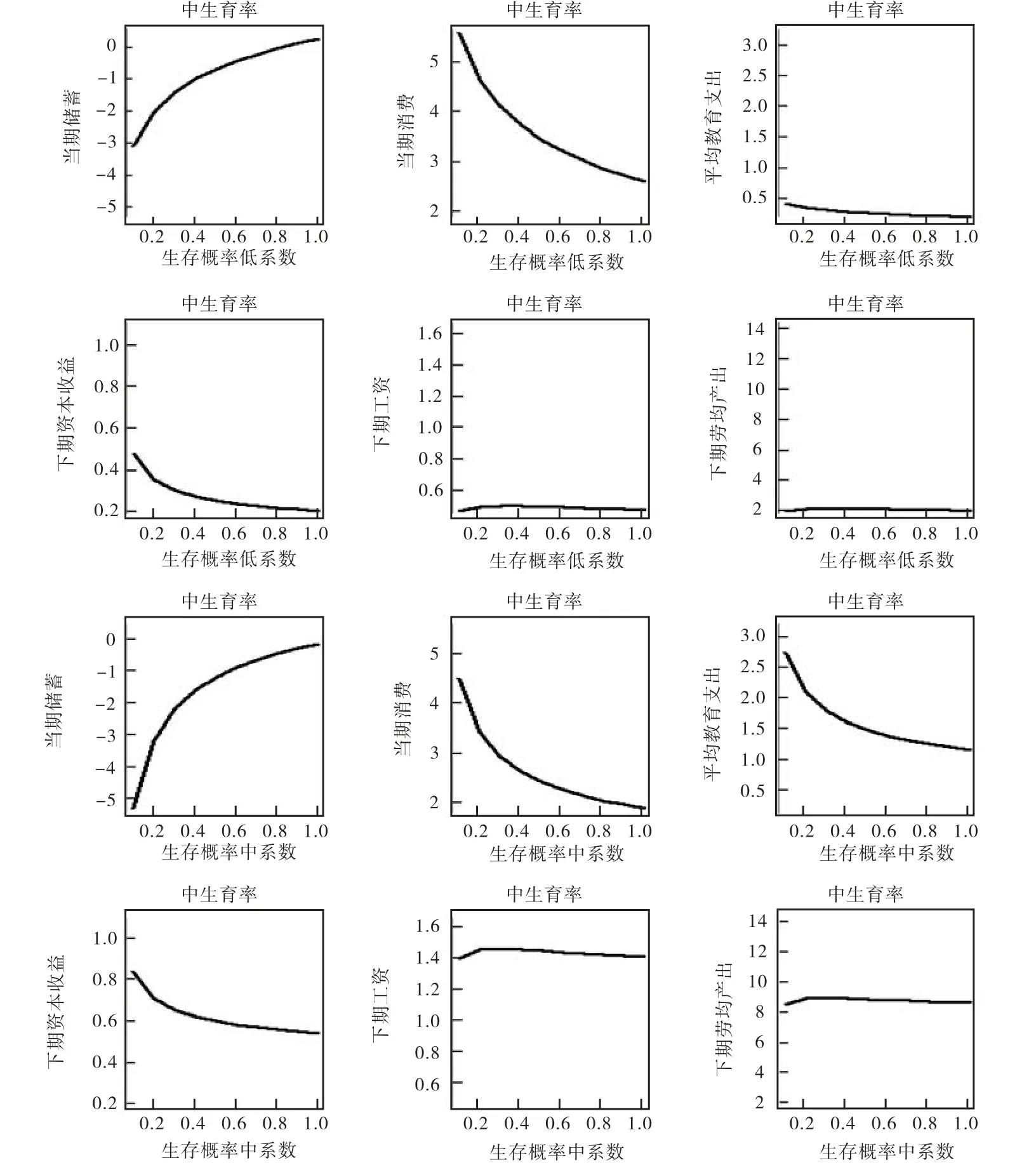
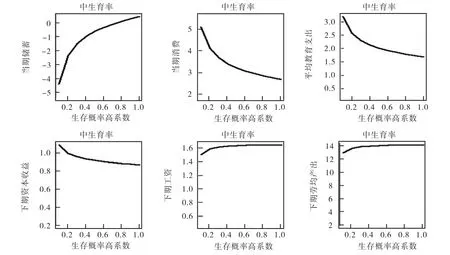
图5 中生育率组

由图 6可以看出，从储蓄的角度，2.6的生育率水平，使得在中系数组下的均衡储蓄为负，而在高系数组下均衡储蓄在一定的预期生存概率下才为正。从资本收益的角度，只有在高系数组下，2.6才是对生育率的相对合理估计，低系数组和中系数组下，2.6的生育率水平使得下期均衡资本收益过低。因此，2.6的生育率水平、0.8的预期生存概率可能才是中国人口结构的合意水平。

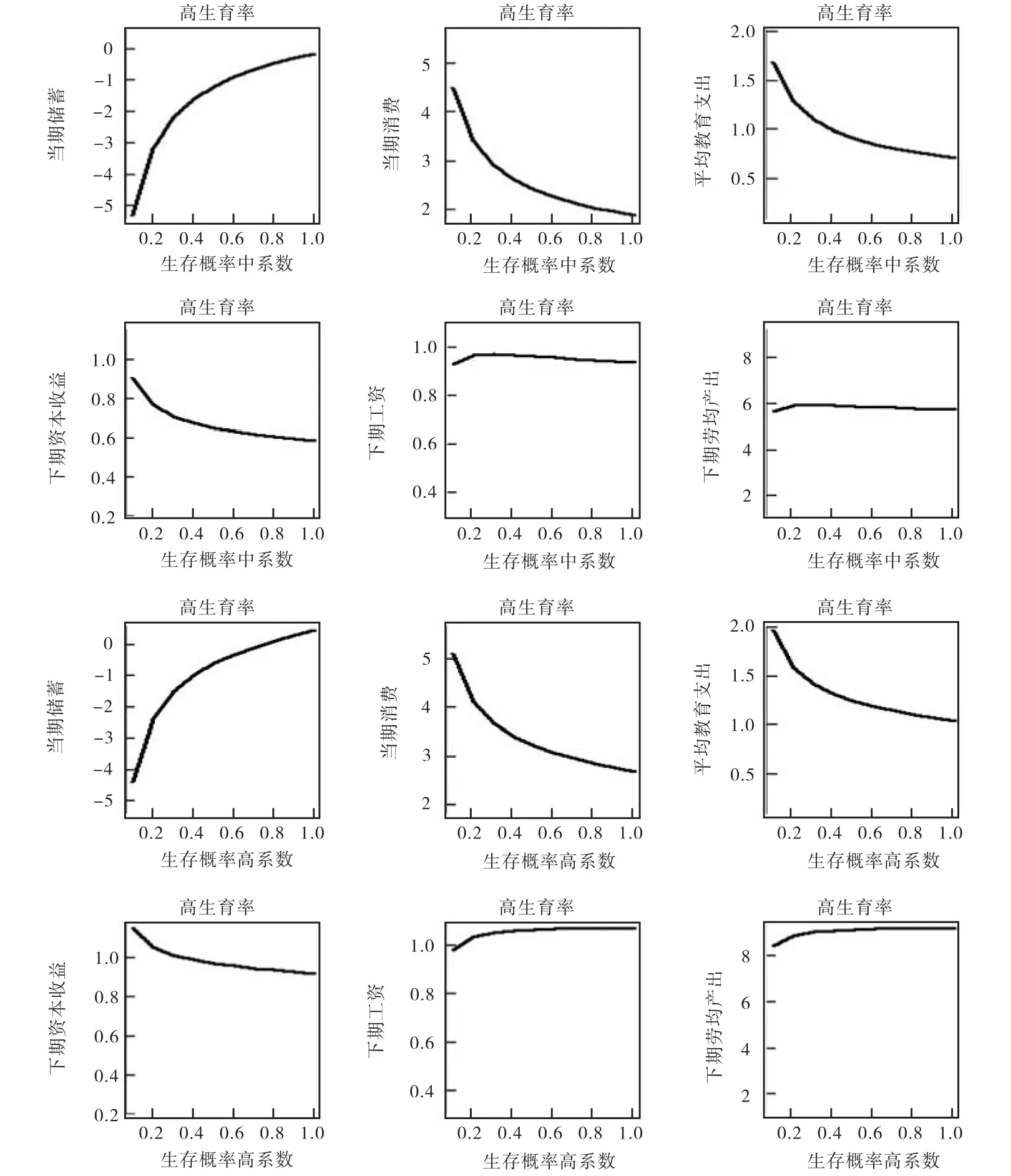
图6 高生育率组

综合图4、图5和图6可以看出，在各系数组下，当期储蓄随预期生存概率的提高而提高，当期消费、当期平均教育投资随预期生存概率的提高而下降，下期工资和人均产出大体上随预期生存概率的提高而先上升后趋于平缓。由此我们可以看出，下期工资的预期生存概率弹性绝对值要小于下期资本收益的预期生存概率弹性，而越是处于高系数下，下期(即老年期)的消费、平均教育投资、下期资本收益、下期工资和下期人均产出越高，这说明高系数组所代表的经济体系运行得更快。

五、结论及政策建议

通过建立综合利他主义信念、古典增长模型、人力资本模型的世代交叠模型，我们分析发现当期消费、当期储蓄和当期总教育投资不随生育率的改变而改变，平均教育投资、下期工资-资本收益比、下期工资和下期人均产出随生育率的提高而下降，下期消费、下期资本收益则随生育率的提高而提高。

其原因在于生育率上升使劳动供给增加，其他条件不变，资本将因此变得相对稀缺，从而下期资本收益上升，下期工资相对下降，劳动效率下降，而由于工资的生育率弹性绝对值大于资本收益弹性的绝对值，下期工资-资本收益比下降，人均产出下降。由于生育率上升使下期资本收益上升，而从未来年轻人得到的转移支付不变，从而代表性消费者老年期的消费上升，代表性消费者的当期储蓄、当期消费和当期教育投资无需任何变动，消费水平就可以得到提高，从而生育率上升不会改变消费者的当期储蓄、当期消费和当期教育投资。

当期储蓄、下期消费和下期工资-资本收益比随预期生存概率的提高而提高，而当期消费、当期总教育投资和平均教育投资随预期生存概率的提高而下降，预期生存概率对下期工资和人均产出的影响取决于系数的相对大小，参数校准的结果表明，大体上，下期工资和人均产出随预期生存概率的提高而先上升后趋于平缓。

其原因在于平均预期寿命延长将使储蓄增加，从而资本供给增加，需求不变，使得下期资本收益下降，下期工资相对上升。由于工资的预期生存概率弹性绝对值小于下期资本收益的预期生存概率弹性绝对值，从而下期工资-资本收益比随预期生存概率的提高而提高，而储蓄增加挤占了当期消费和当期总教育投资。平均预期寿命延长使代表性消费者在青年时期用于老年期消费的储蓄增加，虽然储蓄增加会使资本收益下降，但储蓄上升带来的消费增加的效应超过了资本收益下降带来的消费减少的效应，从而代表性消费者老年时期的消费上升。

我们应当看到，不管一个人是不是利他主义者，只要他/她是一个理性人，以最大化终身效用为目的并且具有足够的预期性，那么他/她的行为模式必然会回到利己主义的路径上去，而这种利己主义路径所决策出的个人最大化效用策略对整个社会而言并不是福利最大化路径，个人行为对整个社会存在负的外部性。因此，政府的介入将必不可少，征收教育税、延长义务教育年限或者将一定比例的税收用于教育投资是政府的较好选择。还应该指出的是，我们的模型缺少了对另一个关键变量——技术进步的分析。可持续的人均产出的提高源于技术进步，因此政府应该做的，一是坚持开放全面二孩政策；二是征收教育税，或者将一定比例的税收用于教育投资，或者延长义务教育年限；三是加大基础科学投资，并实施一些产业政策鼓励私人部门研发投资。

需要指出的是，模型中虽然引入了实施基金制的个人账户，但事实上个人账户只是个人储蓄的一种形式，除非个人账户的税收超过了个人的自发储蓄，否则个人账户的设立无助于提高居民的福利水平，当然这种假设是在个人有完全的预见性的假设上，现实世界中的个人未必有这样的预见性和自制力，因此个人账户的设立是有必要的。