水下振动目标的被动定位方法

李蝉羽,李 环

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳110159)

对水下振动目标信号的捕获,需要完成测定目标距离和方位两项任务.利用被动目标检测的方式测定目标距离，即依据纵波(初至波)、横波、斯通利波的不同频率、振幅、相位等特征，提取不同波到达传感器的时差，利用时差计算目标距离.确定目标方位是根据几何知识来设计的.在二维平面内已知距离的前提下，确定一个目标的具体位置至少需要3个加速度传感器.为了消除直线型传感器布局方式的不足，本文采用五元十字阵传感器的布局方式，给出五元十字阵被动定位原理和定位方程，同时对目标测向和测距的精度进行分析.

传统直线型传感器阵列对水下目标的测向和测距精度受延长线的影响，水下目标会产生偏移，而五元十字阵的水下目标定位方法可以克服直线型传感器布局方式无法确定位于直线型传感器上部或下部区域目标这一缺陷.当被测目标处于直线型分布传感器延长线上或传感器附近时，直线型分布会产生较大的测试误差，而五元十字阵分布很大程度上减小了该误差.将该方法用于水下振动目标探测具有很高的实用价值.

1 时差法测距原理

采用时差法对水下目标进行测距时，需要确定初至波和斯通利波的初始到达时刻.初至波初始到达时刻的确定采用分数维的方法.斯通利波初始到达时刻的提取采用时频联合域分析法.

1.1 时差方位分离测距

在水下地表振动信号中，由于初至波在所有信号中传播速度最快，总会被传感器最先采集到，其次为横波，最后为斯通利波[1].利用传感器采集一系列数据，从中拾取初至波与斯通利波，可得出初至波与斯通利波到达传感器的时间差.由于初至波与斯通利波的波速已提前测定，利用时间差与波速的关系，可以推算振动目标到传感器的距离.时差方位分离测距原理如图1所示.

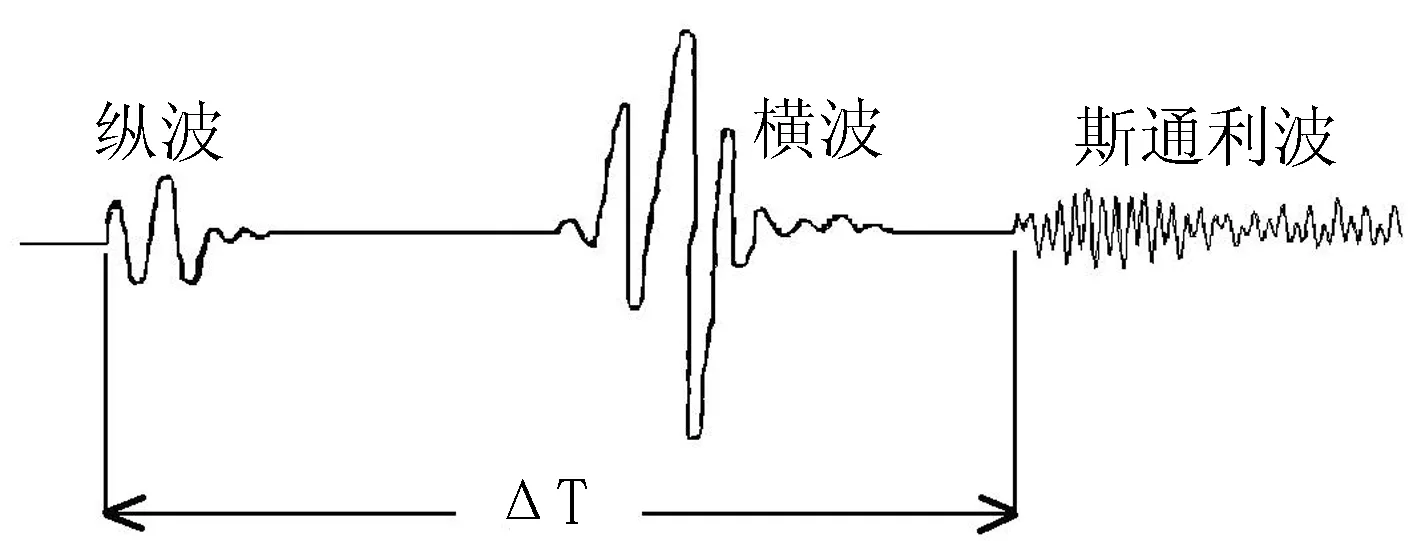
图1 时差方位分离测距原理图

设初至波的传播速度为vp，斯通利波的传播速度为vst，拾取的初至波到达时刻为Tp，提取的斯通利波到达时刻为Tst，则初至波与斯通利波的到达时间差为：

(1)

振动目标与传感器的距离为：

(2)

1.2 采用分形窗口分数维的初至波拾取

由分形相关理论可知，在一条经过处理的分形曲线上，采用长度为w的窗口来覆盖整条曲线上的每一部分，当使用n个窗口覆盖完整的曲线时，该曲线的测量长度为L=nw；当不断改变窗口长度w时，窗口长度与分形曲线的测量长度存在一定的指数关系，即

L=Kw1-D

(3)

式中：K为比例系数；D为分形曲线上的分数维.

(4)

对于采集的原始数据，采用分形窗口分数维的方法来拾取初至波.对信号进行无量纲图形化处理，可得出相应的自仿射曲线.使用分数维的方法描述该自仿射曲线的相关特征.在有效信号(即初至波)来临之前，数据记录的是随机噪声.随机噪声与信号相比振幅较小.当初至波到达时，数据记录的内容将发生变化，其记录的是噪声与初至波叠加后的信号，振幅较大.窗口分数维也将在初至波到来前后发生明显变化.借用这种明显变化的特性能够拾取初至波.

根据分形理论，每个窗口长度w内的分数维变化情况能够表征分形曲线的局部特性，即对应数据曲线的变化情形.这样，通过分析窗口分数维的变化即可确定信号突变的时刻，该时刻即为初至波的到达时刻[2].

1.3 采用时频联合域分析的斯通利波提取

信号的时频联合域分析是针对一维的时间信号的某种分布，构造二维的时间与频率的联合函数.采用这种联合函数，不但可计算信号的时间与频率，也能计算信号的能量密度分布.

时频联合域分析中二次时频分析方法是由能量谱或功率谱演变来的.能量本身就属于二次型，可以更直观地描述时间与能量频率的分布.二次时频以著名的Wigner-Ville分布为主.信号s(t)的Wigner-Ville分布为：

(5)

式中：τ为信号的频域变换时移变量，ω为频域变换中的角频率.

信号s(t)的频谱定义Wigner-Ville分布为：

(6)

式中,υ为信号频谱定义中的频移变量.

设一个信号s(t)可表示成两个信号s1(t)、s2(t)和的形式，即s(t)=s1(t)+s2(t)，则

W(t,ω)=W11(t,ω)+W22(t,ω)+W12(t,ω)+

W21(t,ω)

(7)

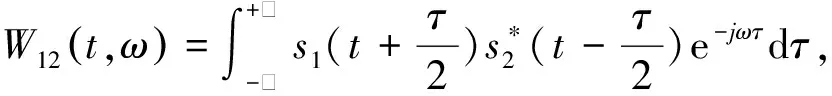
W(t,ω)=W11(t,ω)+W22(t,ω)+2Re{W12(t,ω)}

(8)

式(8)除信号自身项外，还含有两个信号交叉项，且交叉项是实的，混杂于自身项成分之间，幅度为自身项成分的两倍，会对信号的时频联合域分析产生严重影响[3].

因此，对信号数据中的斯通利波提取时，应采用加窗的处理方法，使其信号局部化，重点集中在某个时刻t附近，从而有效减小交叉项的干扰，并保留信号的大部分有效信息.利用两个窗函数来抑制交叉项的干扰，即在式(5)的基础上加入两个窗函数g(u)、h(τ)，可得平滑伪Wigner-Ville分布[3].

信号s(t)的平滑伪Wigner-Ville分布为：

(9)

式中，g(u)、h(τ)是实的窗函数，当且仅当g(0)=h(0)=1时，式(9)为平滑伪Wigner-Ville分布.

对原始信号进行平滑伪Wigner-Ville分布的时频联合域分析，消除原始信号中交叉项的干扰，清晰显示信号在不同频率范围内能量随时间的变化状况，以准确提取目标信号[4].

2 目标定位算法

在目标被动式定位过程中，传感器一般选择阵列布局方式[5].其中，最常用的直线型传感器布局方式如图2所示.

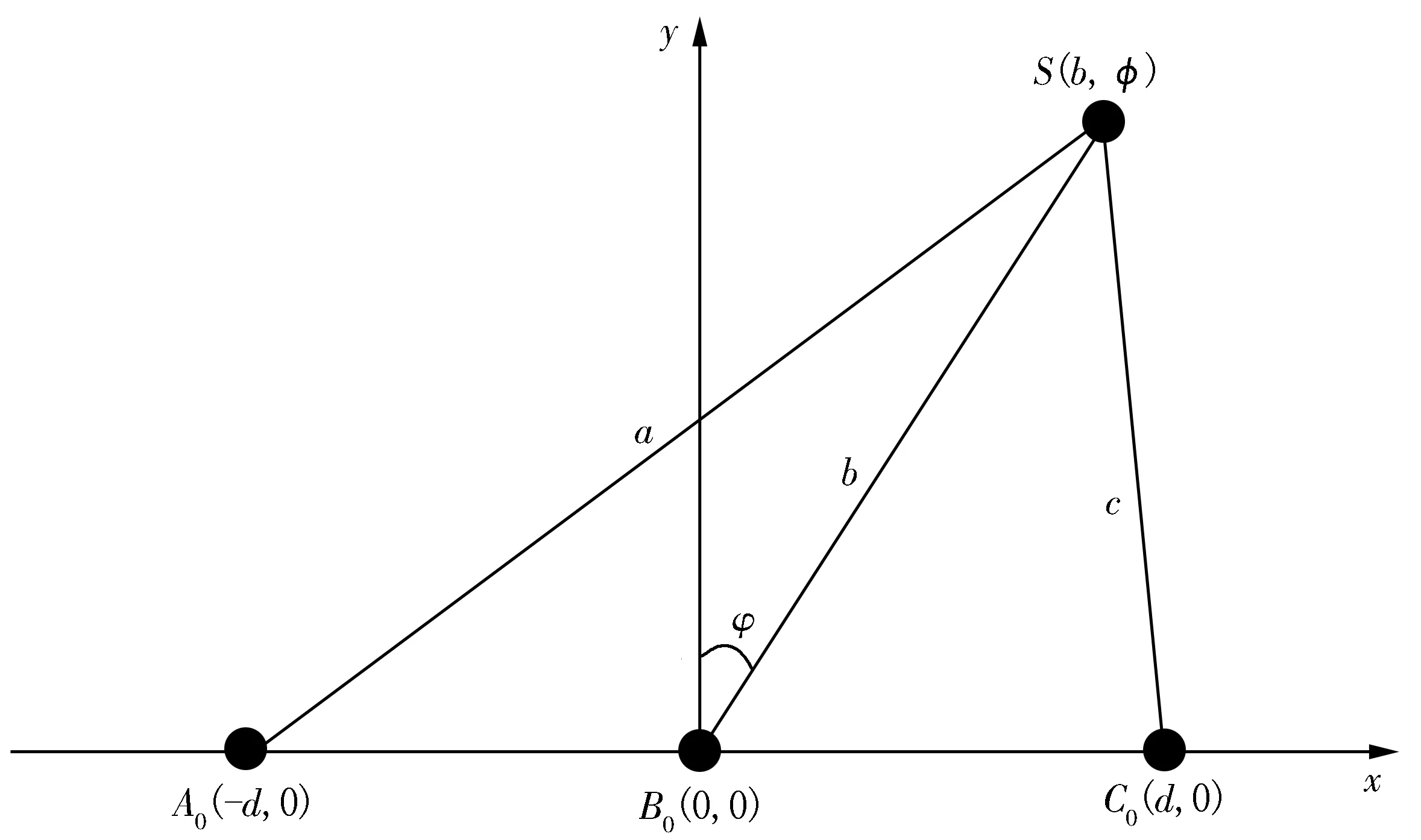
注：A0、B0、C0点为传感器所在位置；S点为目标所在位置。图2 直线型传感器布局方式

图2中:S(b,φ)为振动目标的极坐标形式;A0、B0、C03个位置的传感器之间的距离为d;振动信号的传播速度为v0;A0位置传感器与B0位置传感器采集同一数据的时间差为τab;B0位置传感器与C0位置传感器采集同一数据的时间差为τbc.振动目标的位置如下：

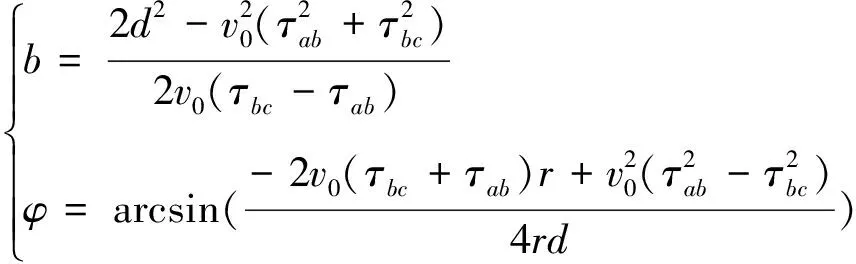
(10)

直线型传感器布阵在实际应用中存在不足.首先，直线型阵列布局方式不能确定被测目标位于直线型阵列的上部区域或下部区域；其次，当被测目标处于延长线上及其附近时，测距结果存在较大误差.图3所示为传感器的五元十字阵布局方式[6].

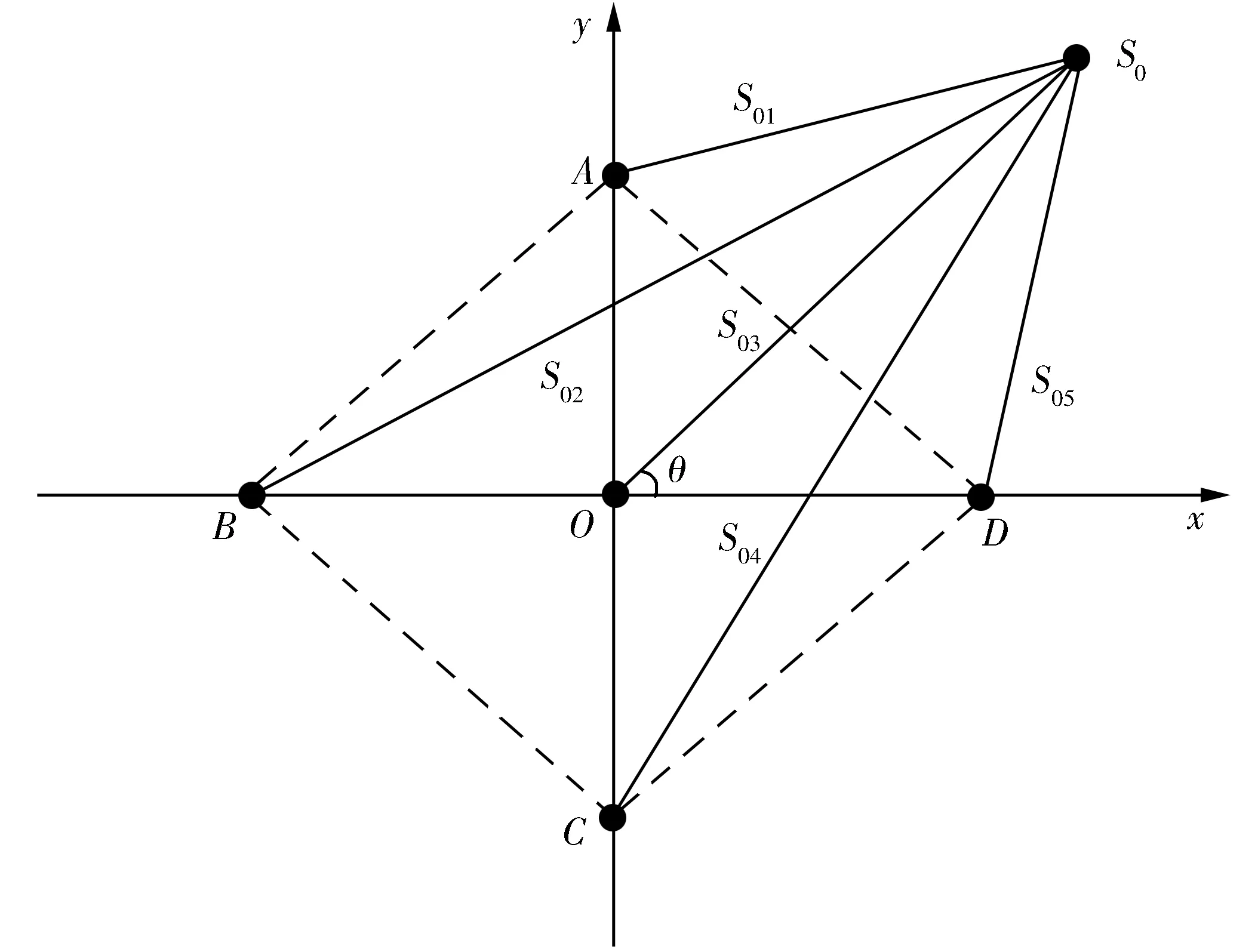
注：S0为产生水底振动信号的声源位置；A、B、O、C、D为水底放置传感器的5个位置；S01、S02、S03、S04、S05分别为各传感器到目标的距离.图3 传感器的五元十字阵布局方式

五元十字阵布局方式需要采用5个传感器.其中一个传感器作为直角坐标系的原点.通过五元十字阵布局的传感器采集的水下目标数据来判断目标所在区域(即位于第1、2、3、4某个象限)，消除了采用传统直线型传感器布局方式的不足.根据几何学原理，如果把每个传感器作为圆心位置(Xi，Yi)，以圆心到目标的定长为半径(记为Si(1≤i≤5))，则通过一系列方程联立，可确定各圆相交于一点，即振动目标的所在位置[6].

测量目标距离时需要对信号做平移操作，将平移后信号y(t)与x(t)作比较，得出曲线重合度最好时的平移量.

两个信号x与y的互相关计算式为:

Rxy(t)=ARss(t-D)+Rwx+wy(t)

(11)

式中：Rss(t)为信号自相关项；Rwx+wy(t)为噪声的互相关序列.当噪声无关时，两个信号的互相关结果Rxy(t)在t=D时存在峰值，此时D为时延.

若用Sxy(f)表示信号x与信号y间的交叉谱，Sxx(f)与Syy(f)分别表示x与y的自谱，则x与y的平方相干函数为：

(12)

最佳极大似然窗为：

(13)

通过W(f)、Sxy(f)的傅里叶逆变换，可得窗函数处理后的互相关结果Rxy(m).通过Rxy(m)的峰值所在位置可获取时延D的初始估值.同时，采用三点插值法，可对时延估计进行优化[6].

在二维平面内，已知一个定点到两点的距离差，若双曲线上任意一目标点到两焦点之间的距离差为定值，则该目标点位于一条双曲线上，该双曲线的焦点是两个传感器所在的位置[7].同理，如果采用3个定点进行数据采集，就会得到两条类似的双曲线，这两条双曲线的交点即为目标所在位置.

此时，即可求得每个传感器到目标S的距离.根据几何学原理，圆的方程为：

(14)

针对图3，分别以x轴、y轴上3个传感器采集的数据作为参考，可得出传感器到目标距离的两组计算方程.

(15)

(16)

对方程组(15)求解，得出的目标S0的坐标为:

(17)

对方程组(16)求解，得出的目标S0的坐标为:

(18)

分别求解方程组(17)与方程组(18)，并对得到的目标S0的两个坐标结果取均值，即可确定目标S0的位置[8].以O位置传感器作为坐标系原点，可计算目标S0到原点的距离，即

(19)

S0的方位角θ为：

(20)

3 仿真实验

通过大水池来模拟水下真实环境，在传感器距目标约50 m内进行定位，设计仿真实验.按照图3所示布局方式，以O为坐标系原点，S0作为振动目标(其坐标为(45，40)，且A点坐标为(0，30)，B点坐标为(-30,0)，C点坐标为(0，-30)，D点坐标为(30，0))进行仿真实验.

实验采集的原始数据含有大量噪声，需要去除噪声干扰.对原始数据进行小波模极大值去噪处理后的信号如图4所示.

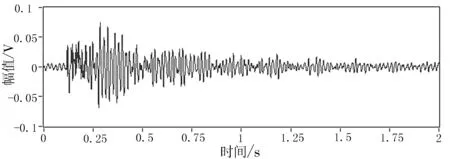
图4 小波模极大值去噪后的信号示意图

窗口分数维的初至波拾取结果如图5所示.

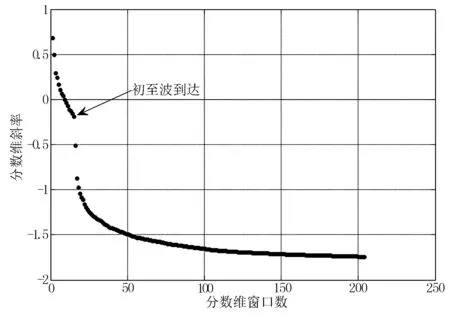
图5 初至波拾取结果

按时频联合域分析的斯通利波提取结果如图6所示.图6中，内圈能量较大，外圈能量较小.

从图6可以看出能量最集中的区域和不同频段内能量随时间的变化情况，也可观察到大部分能量集中在50～60 Hz附近.

图7所示为斯通利波提取结果中能量集中区域局部放大图.

从图7可以看出能量随时间的变化情况及能量集中区域所对应的时间.

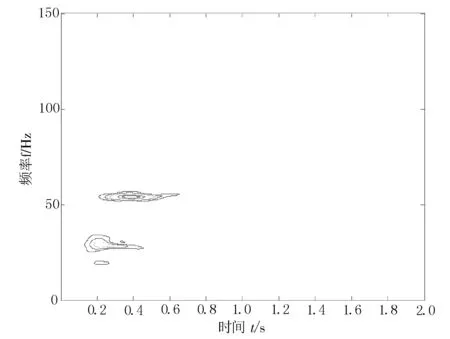
图6 斯通利波提取结果

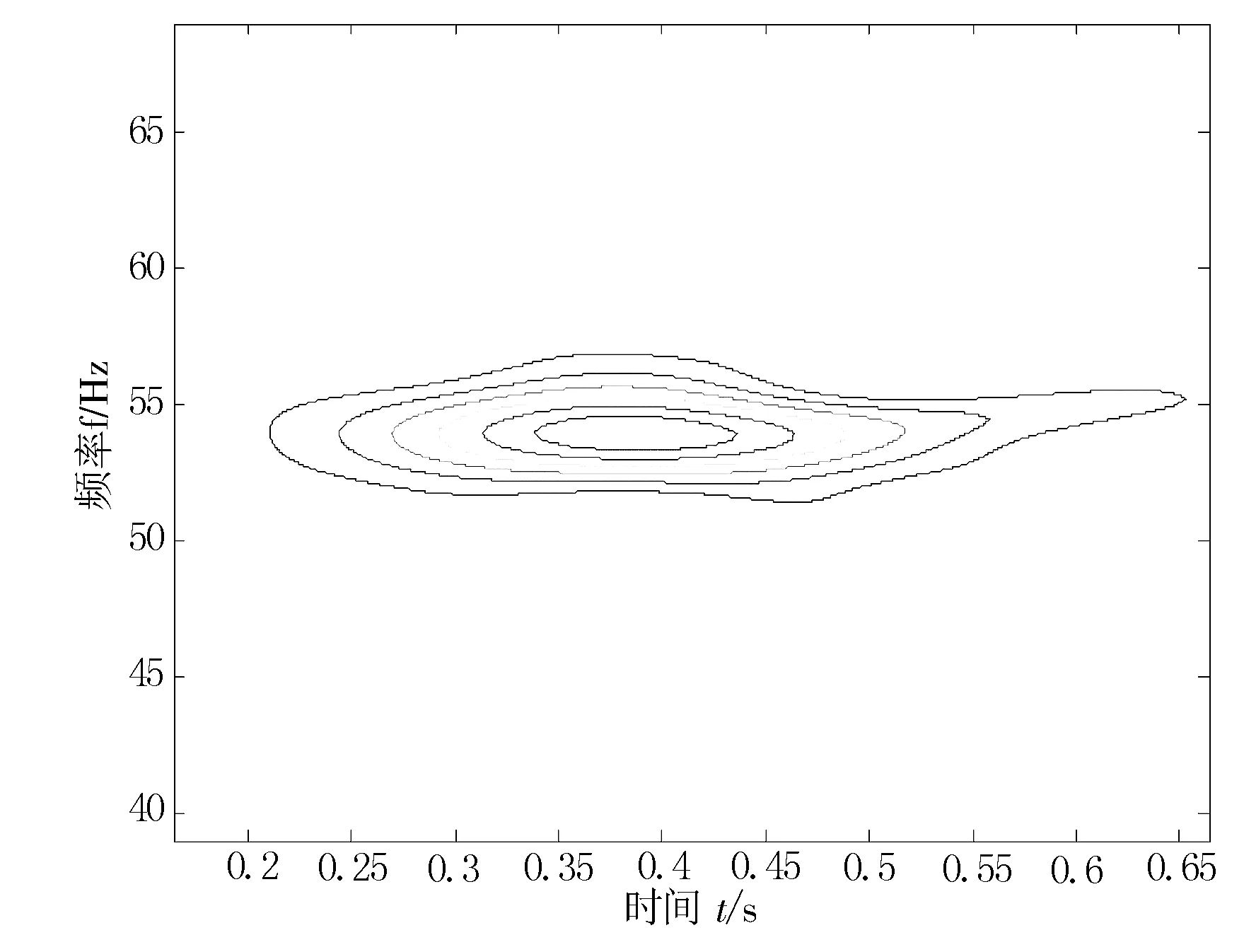
图7 斯通利波提取结果中能量集中区域局部放大图

目标测距的结果如表1所示.

表1 目标测距结果

根据表1数据求得的平均距离误差率为3.4%.

采用五元十字阵计算目标方位角，其精度及时延估计误差与目标所处方位无关，克服了直线型阵列的缺陷。目标方位角的平均误差为3.2°.

针对4组仿真实验数据的目标定位结果如表2所示.

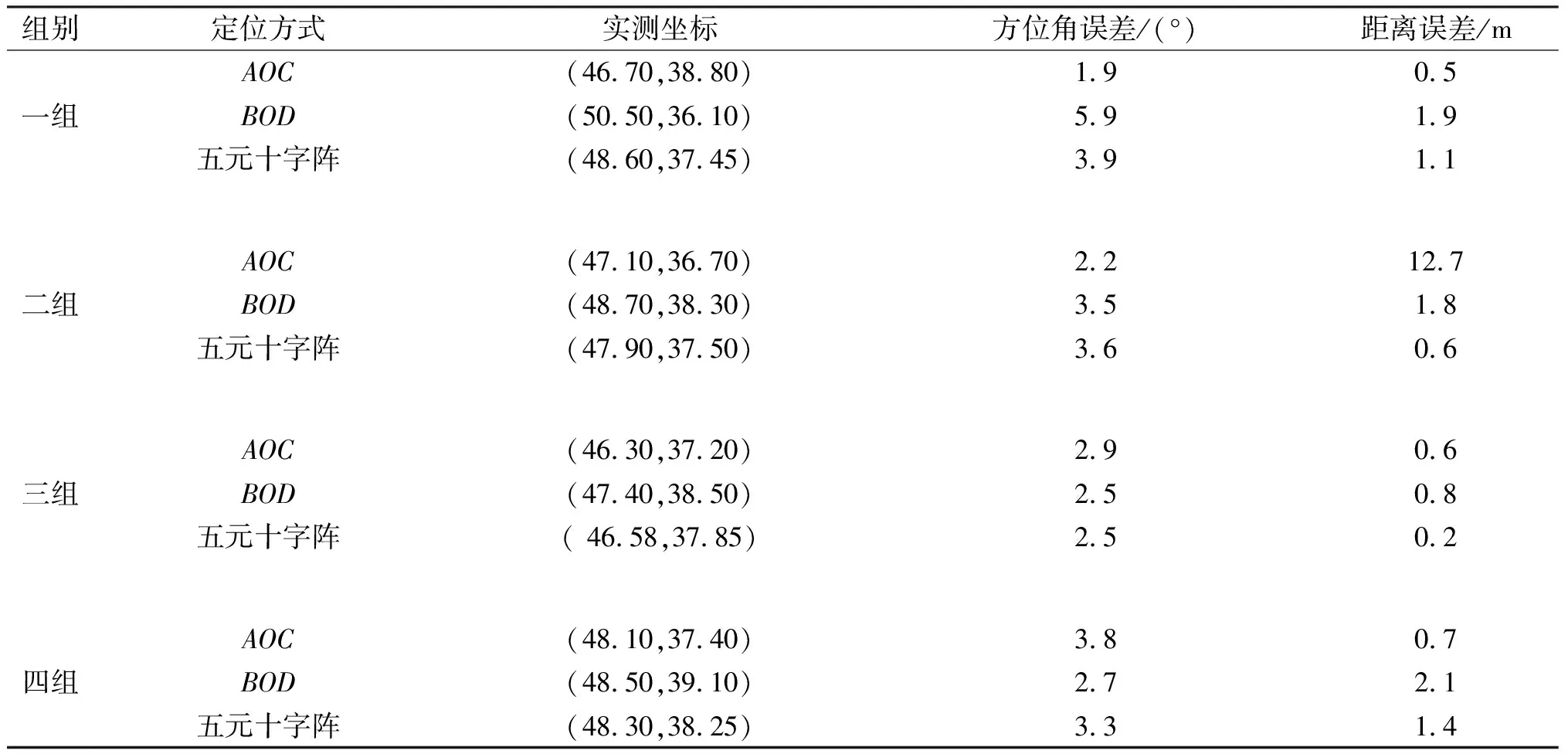
表2 针对4组仿真实验数据的目标定位结果

从表2可以看出，五元十字阵与单独使用AOC、BOD两种直线型的定位方式相比，定位精度大大提高.

分析可知，仿真实验的目标点S0处于第一象限，所测横坐标数值与真实值相比普遍较大，纵坐标数值与真实值相比普遍较小.这是由于AOC、BOD两种直线型阵列结合所导致的.

4 结 论

针对水下环境相对复杂，而传统的直线型阵列定位误差较大，应采用五元十字阵定位方法.该方法能满足水下复杂环境的被动定位要求，有效提高水下目标定位的精度.仿真实验表明，在传感器距目标约50 m内进行的水下目标定位中，五元十字阵定位方法的平均距离误差率为3.4%，目标方位角的平均误差为3.2°.该方法具有较高的实用价值.