高辨识率的成组质量评价新指标GEN

刘乐二

(同济大学 机械与能源工程学院，上海 200092)

成组布局(Group Technology Layout)也称为单元布局(Cellular Layout).成组布局设计包括三方面内容：零件和设备成组构建单元;单元内设备布局(Intra-cell Layout);将各单元布置到车间场地上(单元布局或单元系统布局).这三方面可以分步独立进行，也可同步单元构建和组内布局[1-3]，或者同步进行组内布局和组间布局，还可对这三方面进行同步集成设计.单独进行单元构建时，需要对设备和零件的关系进行分析，选择合适的组数，采用适当的方法将设备和零件归入适当的组，形成设备与零件的组合关系.单元构建的目标是提高设备利用率、降低物流成本.为了达到单元构建目标，需要对已成组的设备零件组合关系(通常可以采用矩阵形式)进行评价，因此需要选用或设计合适的成组质量评价指标.评价成组质量的指标包括：成组效率(Grouping Efficiency,GE)[4]、成组功效(Grouping Efficacy，GF)[5]、加权分组功效(Weighted Grouping Efficacy，WGF)[6]、单元间加权转移(Weighted Intercellular Transfers，WIT)[7]、总键能(Total Bond Energy，TBE)[8]、聚类度量(Clustering Measure，CM)[9]、例外元素的数量加权比例(Volume Weighted Proportion of Exceptional Elements，VWPE)、例外元素的操作顺序比例(Operations Sequences Proportion of Exceptional Elements，OSPE)、单元间操作的实际比例(Actual Proportion of Intercellular Operations，APIO)[10]等.其中GF指标应用较广泛.杨建军对5台设备、10个零件分两步进行分组，并将GF指标作为目标函数[11].李杰等采用聚类算法进行单元构建，使用GF指标评价了成组的效果[12].王建维对单元分组、单元构建进行研究，评价方案时采用了GE、GF指标[13].

成组质量评价指标如果设计的不好，辨识率不高，将难以区分不同成组矩阵的优劣，也就是难以评价成组质量，单元构建的目标也将难以达成.本文提出一种成组质量评价新指标GEN，并将其与GF指标进行比较，以了解新指标的实用性.

1 现有成组质量评价指标

Chandrasekharan等于1986年提出了GE指标[4].其计算方法如下：

GE=q×MU+(1-q)×ODV

(1)

式中：MU(Machine Utilization)即设备利用率，是分组后区块(Cluster)内非0元素与区块内所有元素的比例;ODV(Off-Diagonal Voids)为区块外0元素与区块外所有元素的比例；q为权重系数(0≤q≤1)，表示单元间移动与单元内空位的相对重要性，一般情况下取值为0.5.

成组效率的另一种表达式为：

η=qη1+(1-q)η2

(2)

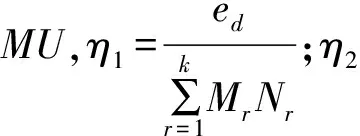
GE指标考虑了例外元素(单元间物料搬运问题)和设备利用率两方面的因素，一度被较多文献(如Askin 1991, Boe & Cheng 1991, Kusiak & Cho 1992)引用，作为对比指标.但是，GE指标本身具有缺陷，区块外元素0的数量太多时GE值会偏高.

Ng分析了GE这一评价指标的不足，认为即使q取值0.1，也会高估设备利用率对成本的影响[6].

GE指标存在缺陷，即使是GE值高达0.75的成组方案，其辨识率也会很低.于是，Kumar等提出了GF指标[5].

GF=(1-PE)/(1+DV)

(3)

式中：PE(Proportion Exceptional Elements)为例外(区块外)非0元素与所有非0元素的比例；DV(Diagonal Voids)为区块内(对角线)元素0与所有非0元素的比例.

GF指标应用较广，多用于评价成组的效果.它可简化表示为：

GF=区块内非0元素数量/(所有非0元素数量+区块内元素0的数量)

(4)

它还可表示为：

(5)

式中,EE为例外元素总数.

Ng在文献[6]中对GF指标进行了改进，提出了加权分组功效(Weighted Grouping Efficacy，WGF)指标，并将其表示为：

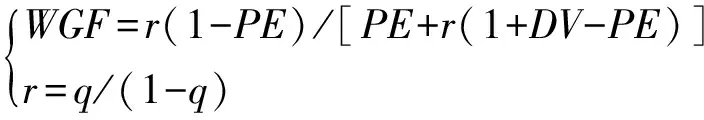
(6)

当r=1时，WGF=GF，q=0.5.

本文将式(6)简化为：

WGF=(1-PE)/(1+DV-c×PE)

(7)

式中,c为系数.当c=0时，WGF=GF.

2 成组质量评价新指标GEN

本文提出一种辨识率较高的成组质量评价新指标GEN.

(8)

一般情况下，β=0.5.本文后续示例中β均取0.5.

3 指标GEN与GF的辨识率比较

3.1 简单矩阵中指标GEN和GF的辨识率比较

以文献[10]中矩阵(图1)为例，对GEN与GF的辨识率进行比较.各矩阵的成组质量指数如表1所示.

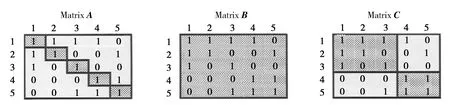
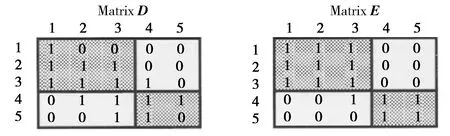
图1 示例矩阵

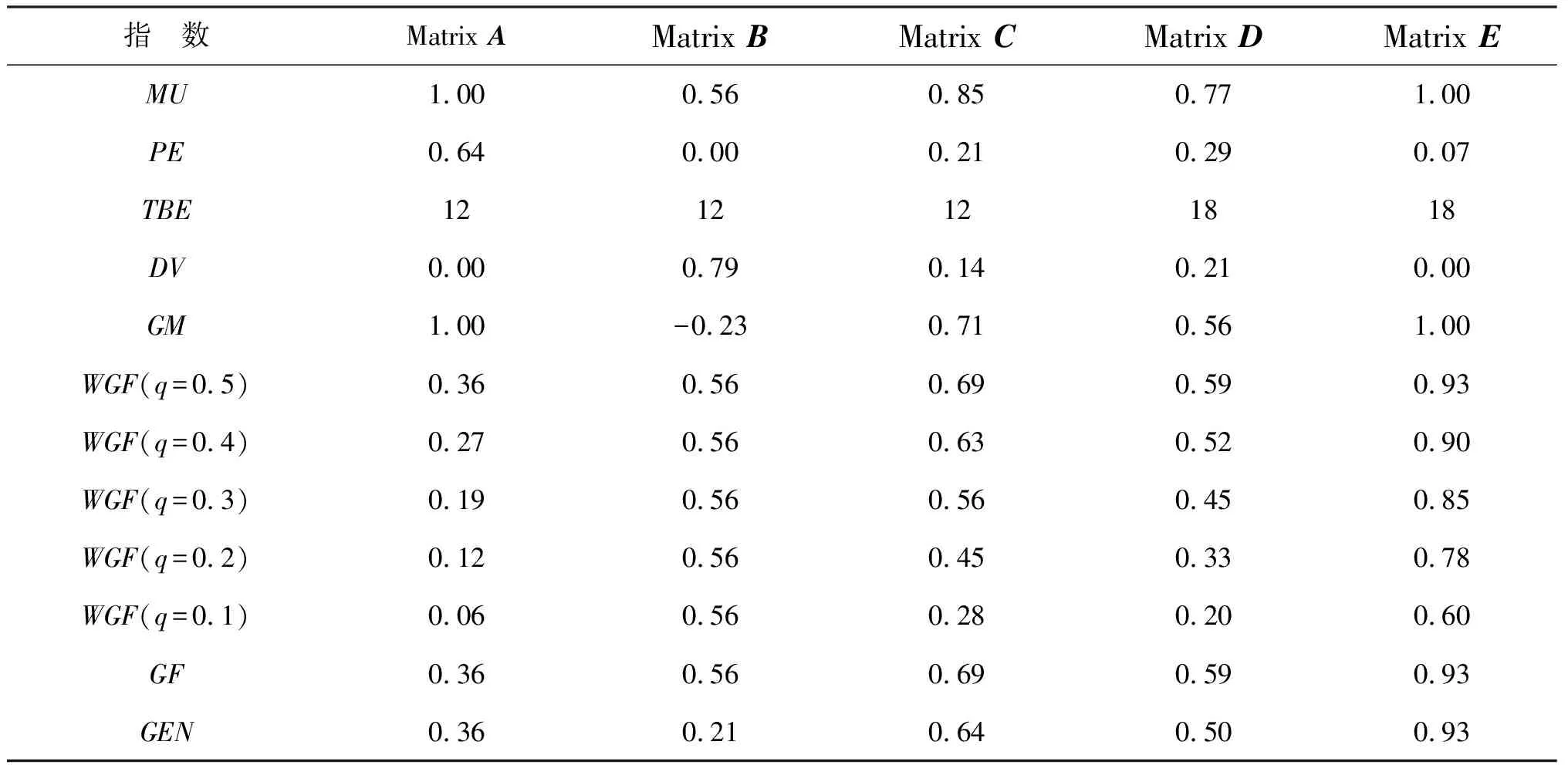
表1 各矩阵的成组质量指数

注：表中数据单位为1.

从表1可以看出：GF值在B、C、D矩阵之间差异不大，特别是B、D矩阵之间相差很小(差值仅为0.03)；而GEN指标在B、C、D矩阵之间差异较大，特别是B、D矩阵之间相差很大(差值达0.29).由此可见，此例中指标GEN比GF辨识率更高.

3.2 某车间设备零件成组方案中指标GEN和GF的辨识率比较

对某车间的设备零件进行成组处理，形成20个成组方案.各成组方案的GEN值和GF值如表2

所示.

表2 各成组方案的GEN值和GF值

在这20个成组方案中，GEN的平均值为0.291 55，GEN的标准差为0.215 8；GF的平均值为0.406 7，GF的标准差为0.058 5.GEN标准差是GF标准差的3.69倍(0.215 8/0.058 5).将GEN值、GF值描点到平面坐标系中，并进行二次拟合(图2).该图可以表示GF值与GEN值之间的关系.

对于图2中两种指标的关系曲线，通过二次多项式拟合可得：

GF=0.310×GEN2+0.222×GEN+0.301

(9)

拟合后方差为：R2=0.954 2.

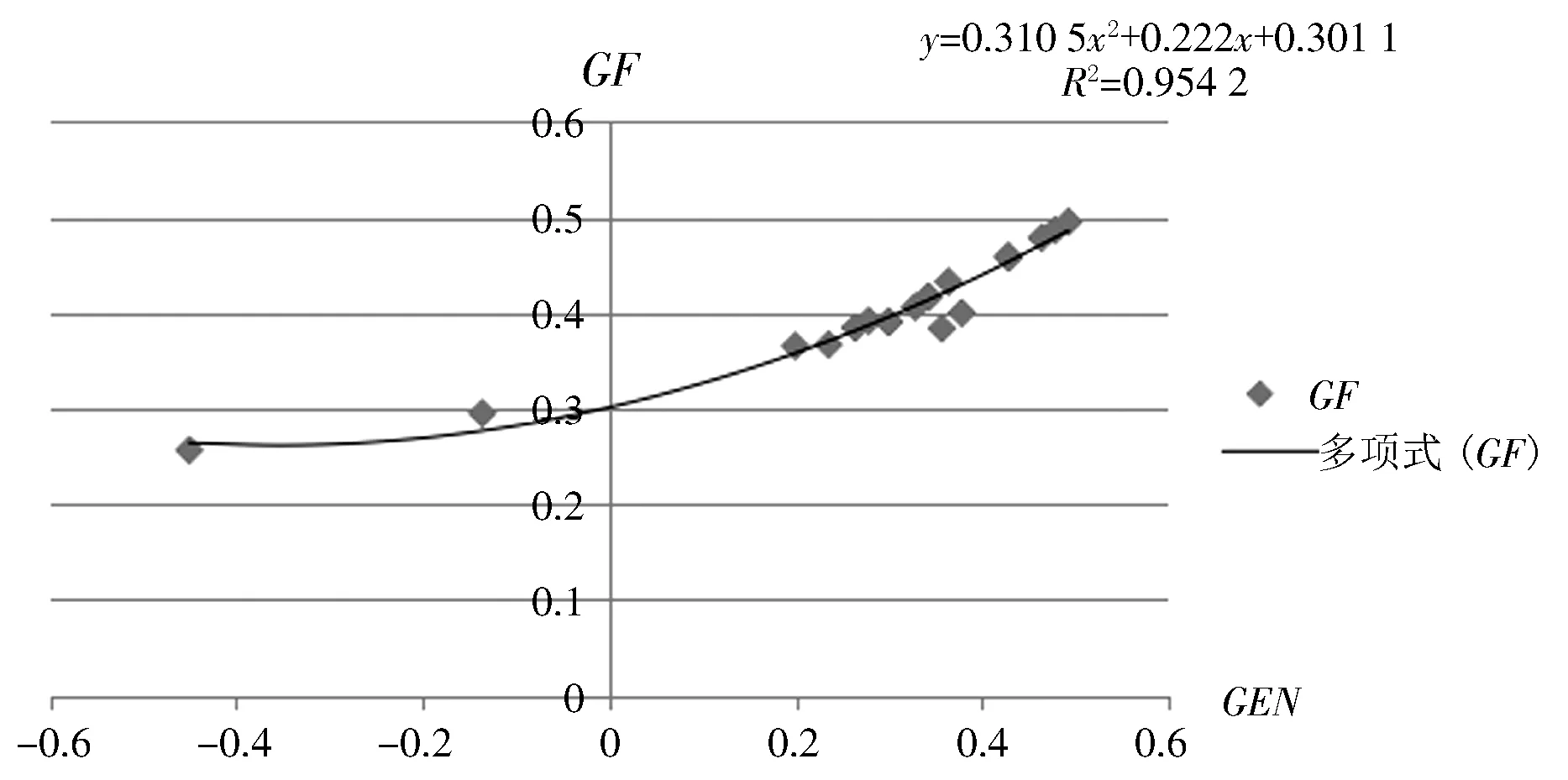
图2 GF值和GEN值的关系

变换坐标，进行一次拟合，可得图3所示的指标GEN与GF辨识率比较曲线.

对于图3中两种指标的关系曲线，通过线性拟合可得：

GEN=3.402×GF-1.092

(10)

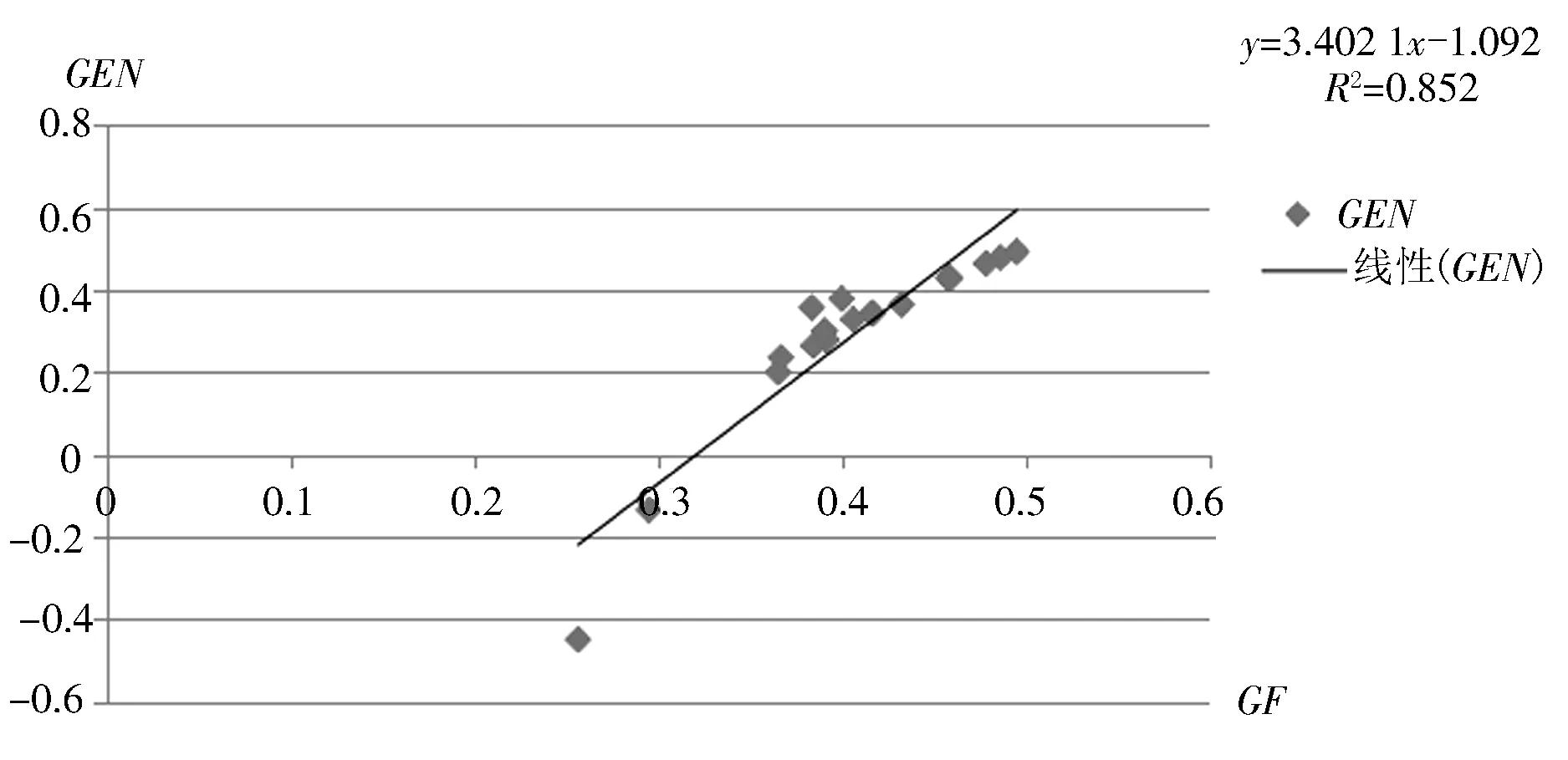
图3 指标GEN和GF的辨识率比较曲线

拟合后方差为：R2=0.852 0.

一次拟合直线的斜率为3.402.该值接近于GEN标准差与GF标准差的比值3.69.由此可见，在该车间各成组方案中，指标GEN比GF的辨识率更高.

3.3 随机矩阵中指标GEN和GF的辨识率比较

针对区块内非0元素数量、区块内元素0的数量、区块外非0元素数量，取10 000组1～20的随机整数，并对各组分别计算GEN值、GF值.GF值在0.02～0.91之间，GEN值在-4.50～0.93之间.

将GEN值、GF值描点到平面坐标系中,并进行一次、二次拟合.数据出现次数越多，坐标系中点就越密集.GEN值、GF值的分布及一次、二次拟合曲线如图4所示.

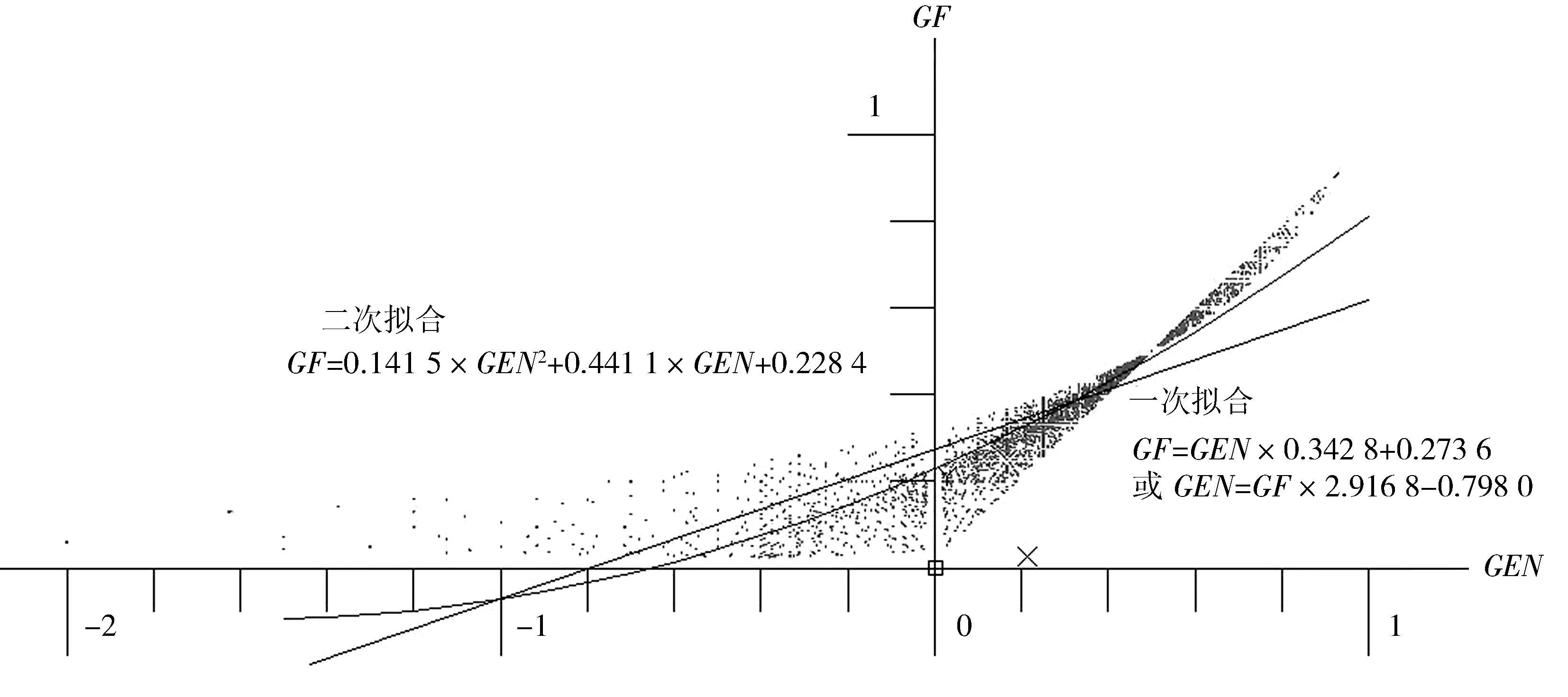
图4 GEN值、GF值的分布及一次、二次拟合曲线

对于图4中两种指标的关系曲线，通过二次多项式拟合可得：

GF=0.141 5×GEN2+0.441 1×GEN+0.228 4

(11)

对于图4中两种指标的关系曲线，通过线性拟合可得：

GF=0.342 8×GEN+0.273 6

(12)

将式(12)变换可得：

GEN=2.916 8×GF-0.798 0

(13)

可将10 000组随机矩阵数据中各GF值和出现的频次(组数)以图形表示(图5).GF的平均值为0.334 8，标准差为0.170 1.

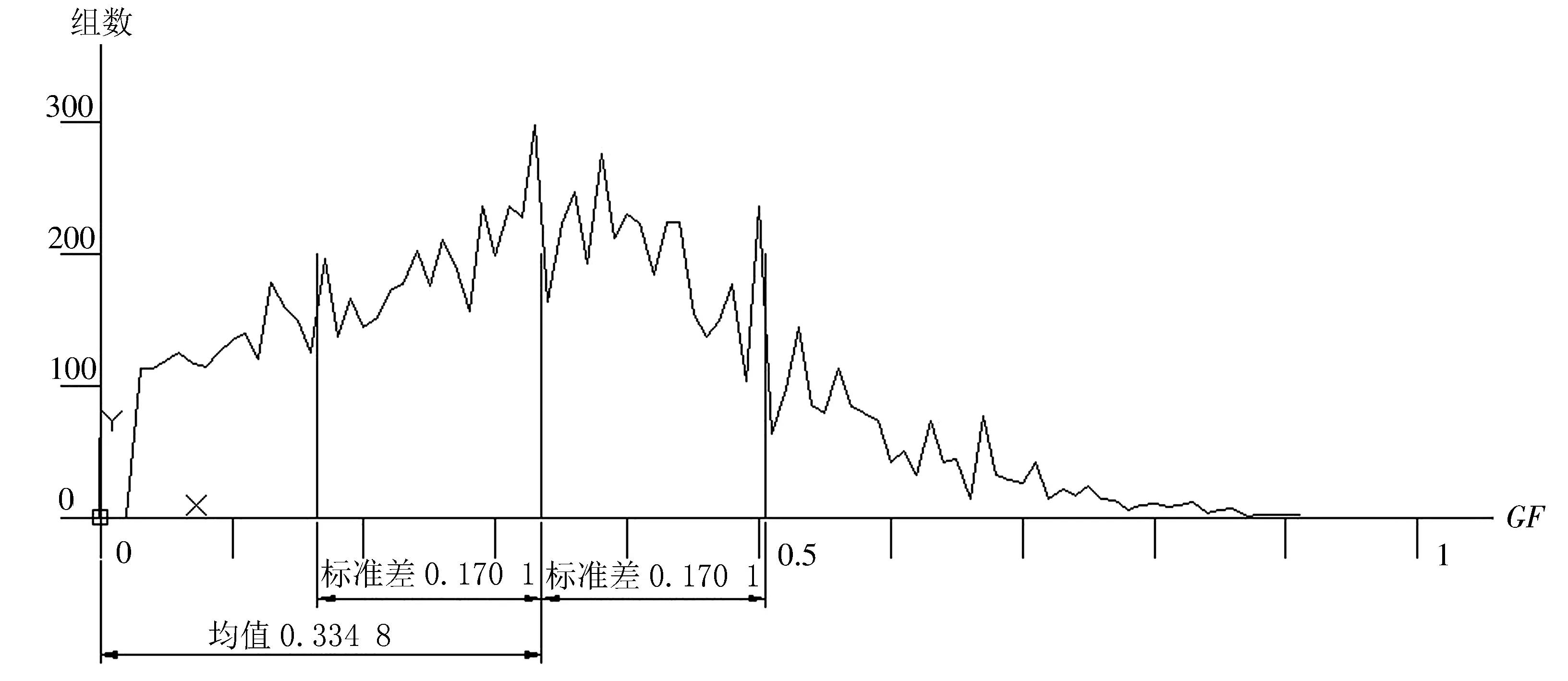
图5 GF值和出现频次的关系

可将10 000组随机矩阵数据中各GEN值和出现的频次(组数)以图形表示(图6).GEN的平均值为0.178 9，标准差为0.403 6.

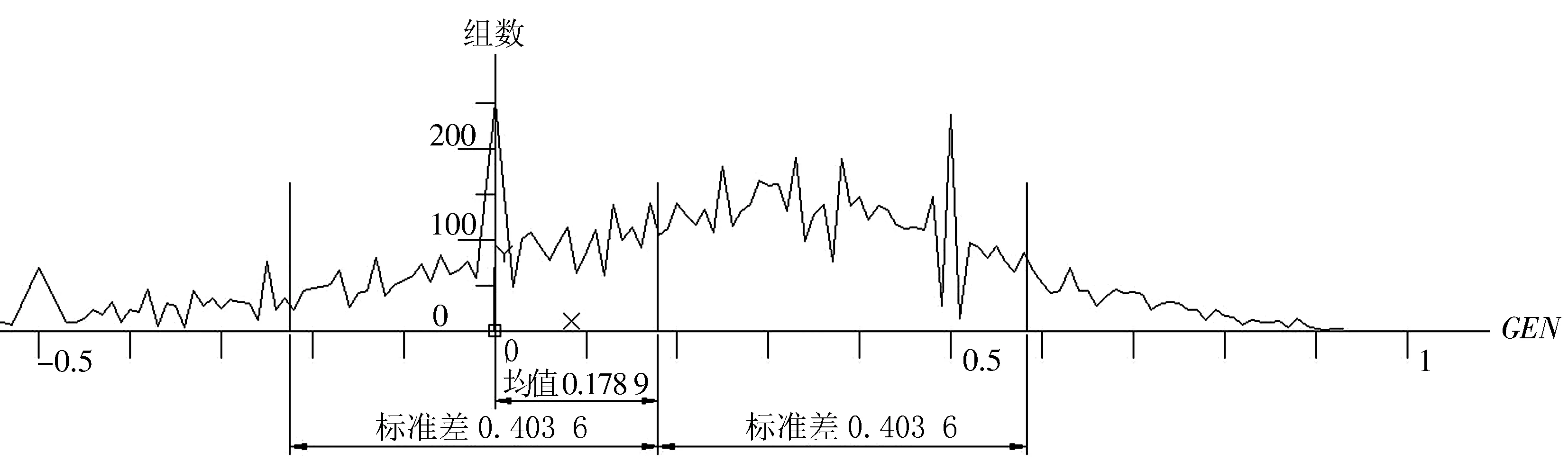
图6 GEN值和出现频次的关系

比较图5、图6可知，GEN标准差是GF标准差的2.37倍(0.403 6/0.170 1)，也就是说GEN值分布更加分散，而GF值分布相对集中.GEN标准差与GF标准差比值为2.37，一次拟合直线的斜率为2.916 8，表明10 000组随机矩阵数据的GEN指标比GF指标辨识率高.

4 结束语

零件和设备成组构建单元是成组布局设计的重要环节.了解所构建成组矩阵的优劣，需要辨识率高的成组质量评价指标.现有GF指标应用广泛，但辨识率并不高.本文提出一种成组质量评价新指标GEN，以相关文献中的矩阵、某车间设备零件的20个成组方案、10 000组随机矩阵数据为例，对指标GEN与GF的辨识率进行了比较.比较结果表明，新指标GEN的辨识率明显高于GF指标.成组质量评价新指标GEN可有效应用于成组质量评价和单元的构建.