堤防渗透计算方法对比分析
2019-05-27罗志雄
罗志雄
(江西省水利科学研究院,江西 南昌 330029)
0 前言
堤防是水利工程中一种重要的水工建筑物,渗流是影响堤防安全运行的重要因素。对于堤防渗透计算的方法主要有两类,即流体力学的方法和水力学法[1]。流体力学的方法是建立在比较精确的数字分析的基础上,但是在大多数情况下这种计算方法比较复杂,因此应用不广泛。水力学法计算工作较为简单,主要包括包括楔形体法、竖直坡面法等,但是精度较差一些,在实际工程中应用较多。
随着科技进步,计算机的发展,有限元法[2]由于其能更好的适应复杂的边界条件和堤身、堤基、各向异性等不同情况,在堤防的渗透计算中运用越来越广泛。本文采用基于有限元法的数值计算软件GeoStudio对堤防进行渗透计算,同时与楔形体法、竖直坡面法计算结果进行对比分析,为实际工程渗透计算提供参考依据。
1 工程概况
某均质土堤堤顶高程40.0 m,堤高10.0 m,堤顶宽度7.0 m,堤前水位38.0 m,堤后水位30.5 m,土堤下游无排水设备。堤身为人工填土,其渗透系数k=2.89×10-4cm/s,土体含水量27.1%,湿密度1.82 g/cm3,干密度1.37 g/cm3;堤基为粘土,其渗透系数k=2.38×10-6cm/s,土体含水量 20.4%,湿密度 1.73 g/cm3,干密度1.31 g/cm3。堤身上游边坡坡率1∶3.5,下游边坡坡率1∶2.5,见图 1。

图1 均质土堤断面图
2 渗透计算
2.1 楔形体法
2.1.1 计算原理
楔形体法进行渗透计算时,采用两个竖直平面将堤身分成3个部分:上游侧楔形体,中间部分及下游侧楔形体。此时一个竖平面通过上游侧堤肩,另一个竖直面通过浸润线下游侧出逸点。堤身浸润线、渗流量和下游侧堤坡面任意高度处的渗透水力坡降的计算简图(图2)及公式如下[1]:

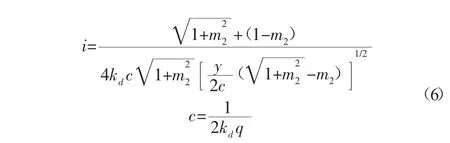
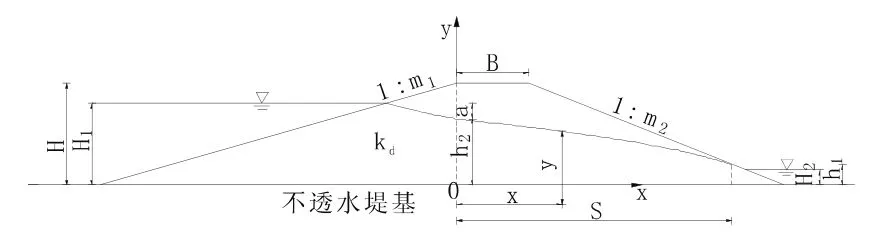
图2 楔形体法的渗透计算简图
2.1.2 计算结果
根据图2和公式(1)~(6)可得,该堤防浸润线与下游堤坡的交点处纵坐标为h1=1.8563 m,浸润线在0y轴上的纵坐标为h2=6.5152 m,浸润线与上游堤坡交点和与0y轴交点之间的竖直距离为a=1.4848 m。堤身单宽渗流量为0.1574 m3/d,浸润线方程为下游侧堤坡出逸坡降为i=0.2939。
2.2 竖直坡面法
2.2.1 计算原理
为了简化渗透计算,常常使用竖直的堤坡面来代替实际的倾斜的堤坡面。此时竖直堤坡面距上游水面与实际堤坡交点的水平距离为ΔL,ΔL的长度应使得流经竖直堤坡面到通过上游面堤肩的竖直平面之间这一段距离内的渗透水流的水头损失,等于通过实际堤坡面流经上游侧楔形体的渗透水流的水头损失。堤身浸润线、渗流量和下游侧堤坡面任意高度处的渗透水力坡降的计算简图(图3)及公式如下[1]:
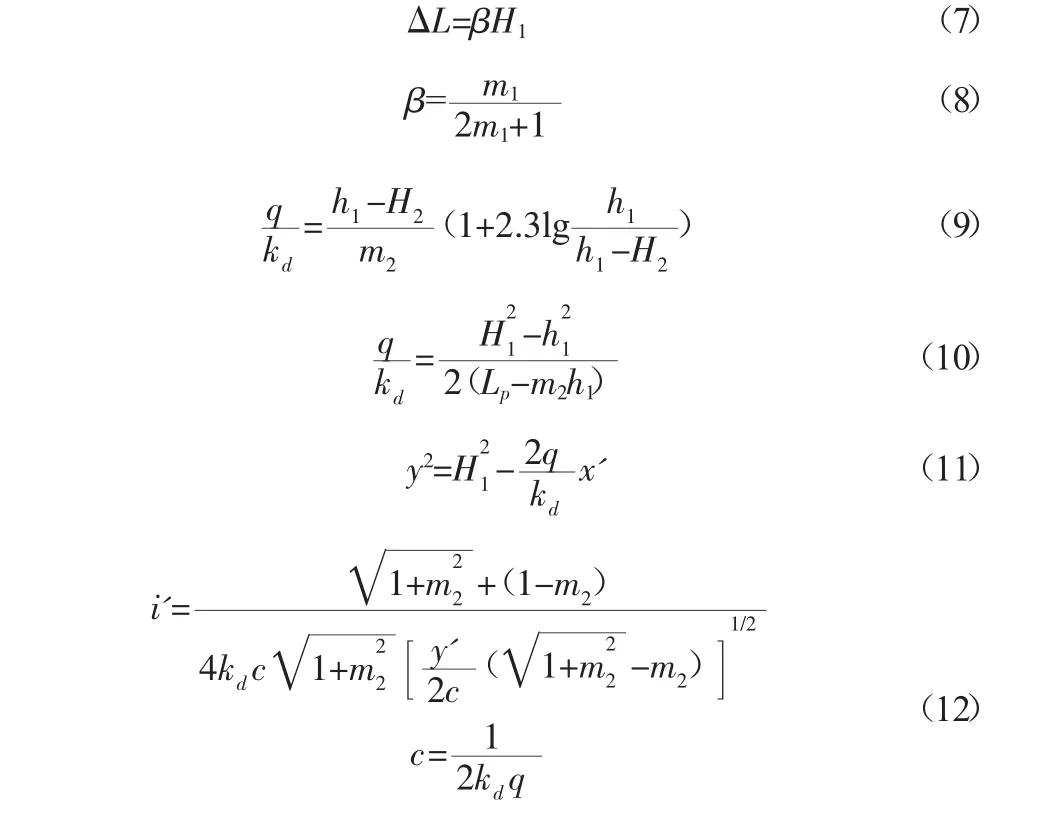
图3 竖直坡面法的渗透计算简图
2.2.2 计算结果
根据图3和式(7)~(12)可得,该堤防竖直坡面距上游水面交点的水平距离ΔL=3.5 m,浸润线与下游堤坡的交点处纵坐标为h1=2.2970 m,堤身单宽渗流量为0.1997 m3/d,浸润线方程为下游侧堤坡出逸坡降为i'=0.2976。
2.3 有限元法
2.3.1 计算原理
本文有限元[2~6]计算分析堤防渗透时采用GeoStudio,其渗流计算基本方法符合达西定理,达西定理在非饱和区和饱和区都是一样的,其二维平面渗流方程如下:

式中:h为总水头;kx为x方向的渗透系数;ky为y方向的渗透系数;Q为应用边界渗流量;θ为土体储水变化率;t为时间。
等式右端为土体储水变化率,该方式适用于瞬态分析。如果等式右端为0,即土体储水不变时,即为稳态分析。渗透计算简图见图4。

图4 有限元法的渗透计算简图
2.3.2 计算结果
采用GeoStudio中SEEP/W模块进行渗透分析计算,按照实际情况绘图,并设置相应边界条件,划分有限元网格。在材料模型选择时,堤身采用饱和/不饱和模型,堤基采用饱和模型。经分析计算,可得该堤防浸润线与下游堤坡的交点处纵坐标为h1=3.3333 m,堤身单宽渗流量为0.2784 m3/d,此处浸润线方程中x和y与楔形体法一致,采用excel数据拟合曲线得y=-0.0045x2-0.0649x+7.4501,下游侧堤坡出逸坡降为i=0.3296。
3 方法比较分析
结果见表1和图5。

表1 三种方法计算结果对比表

图5 各计算方法下浸润线结果图
由表1和图5可知:
(1)由楔形体法和竖直坡面法计算成果可知,下游侧堤坡出逸坡降值差异较小,两者误差不足1.3%;但是下游侧堤坡出逸点高度和堤身单宽渗流量数值差异较大,两者误差皆超过20%。两者之所以出现差异,其原因是竖直坡面法是将竖直的堤坡面来代替实际的倾斜的堤坡面,存在一定差异。
(2)由有限元法和水力学法(楔形体法、竖直坡面法)计算结果可知,有限元法和水力学法计算所得的浸润线变化趋势是相同的,但有限元法所得浸润线稍高。下游侧堤坡出逸坡降值差异较大,两者误差达12%,且下游侧堤坡出逸点高度和堤身单宽渗流量数值差异大,两者误差皆超过50%。两种方法所得结果之所以出现差异,其原因是有限元法考虑了渗流边界条件和堤身、堤基材料特性,但水力学法基本假定是堤内的浸润线的位置不取决于土料的种类,而是取决于堤身横断面的几何尺寸。
4 结论
(1)有限元法和水力学法计算所得的浸润线变化趋势是相同的,但有限元法计算出渗流量、出逸坡降及浸润线较水力学法计算结果偏大和偏高,分析主要是由于有限元法考虑了渗流边界条件和堤身、堤基材料特性,但水力学法基本假定是堤内的浸润线的位置不取决于土料的种类,而是取决于堤身横断面的几何尺寸,存在局限性,与实际情况存在差异。
(2)建议堤防实际工程渗透计算中,在水力学法计算的基础上,同时采用有限元进行数值模拟对比分析研究,确保计算的准确性。
