高精度陀螺仪在超长铁路隧道贯通误差预计中的应用研究

时丕旭

(中铁第一勘察设计院集团有限公司，陕西西安 710043)

随着我国铁路建设工作的不断推进，目前已涌现出一大批超长铁路隧道，如青藏铁路关角隧道、西康铁路秦岭一线隧道等。川藏铁路的开工建设，更是为隧道工程测量提供了广阔的天地。张国良[1]提出了在隧道贯通测量中加测陀螺边的方法；马骥等[2]以柠条塔隧道为依托，对陀螺定向技术在矿山测量中的应用进行研究；付宏平等[3]对长大隧道贯通误差预计方法进行了分析。但以往研究对于超长铁路隧道洞内陀螺定向边的施测位置及数量等鲜有介绍，以下结合具体工程对隧道内的施测陀螺边最优位置及数量进行分析。

在隧道贯通施工之前，往往先进行洞内贯通误差预计，贯通误差受洞内、洞外两方面控制测量的误差影响。为控制横向贯通精度，目前广泛采用了陀螺定向技术，在洞内控制网中加测陀螺边，能有效控制导线方位误差的积累，可使隧道的横向贯通精度有明显提升。在超长铁路隧道布设洞内导线时，大概每3 km加测一条陀螺边；另外，斜井与正洞贯通及短边处均需进行陀螺定向测量，用以提高洞内控制网精度，满足铁路隧道贯通施工的精度要求。

1 隧道横向贯通误差预计

对于超长隧道，洞外控制网一般采用GPS技术布网，并以此为依据，在洞内布设导线网，通过全站仪实测导线及平差得到导线点坐标。在超长隧道的贯通测量中，其误差主要来源于洞内导线测量的角度误差和边长误差。导线法是隧道贯通误差预计最为常见的方法。隧道贯通误差由洞内、洞外两部分控制测量引起，洞外GPS测量精度一般较高，这里仅对洞内测量误差进行分析。

1.1 洞内导线测量误差影响

(1)角度测量误差的影响

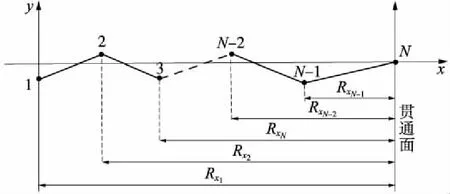
图1 角度误差对横向贯通的影响

隧道洞内导线如图1所示，角度误差引起的横向贯通误差值[4]公式为

(1)

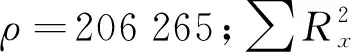
用该方法计算直伸型导线横向贯通误差是严密的。由于隧道一般采用两端相向掘进，因此，角度测量影响值可表示为

(2)

(2)边长测量误差的影响

如图2所示，线段AB的边长测量误差为ml，其投影长度为dy，边长误差的影响值可表示为

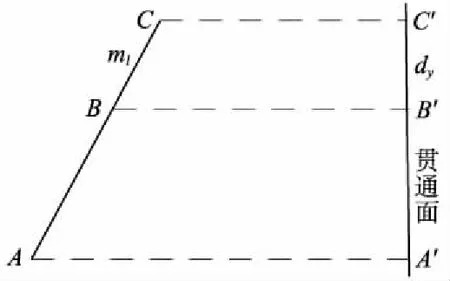
图2 边长误差引起的横向贯通误差

(3)

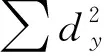
综合分析角度和边长误差，其贯通影响值可表示为

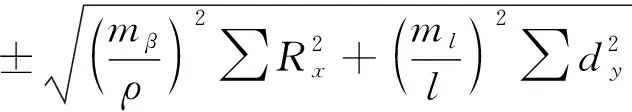
(4)

1.2 施测陀螺定向边隧道贯通误差预计

等精度观测N条陀螺边(如图3所示)，其中误差为mα1，mα2,mαN，此时地下导线可分为N段附合导线，各段的重心分别为OI，OII,ON，最后为一段为D点至K点的支导线。

由导线测量角度误差引起的横向贯通误差值可表示为

(5)

式中，η为导线点与各自重心点的连线在横轴上的投影，Ry′为导线点与原点的连线在横轴上的投影。陀螺定向误差影响值为

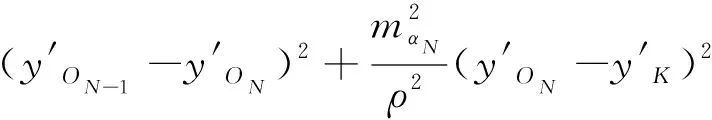
(6)

若mα1=mα2=…mαN=mα，则有

(7)

2 工程实例分析

2.1 工程概况

兰渝铁路西秦岭隧道全长28.8 km，是我国铁路第二长隧道[6]。该隧道洞外采用GPS布网，洞内布设成交叉导线网的形式。工程掘进主要采用TBM掘进机施工，为了保证工期和规避地质环境风险，隧道进口段采用钻爆法开挖施工。

该隧道左线开挖施工面除进、出主洞口外，为了通风、出渣及输送施工材料，在隧道中部另增设两座斜井增加施工工作面。目前，进、出口主洞口分别与毗邻斜井顺利贯通，未贯通段(TBM施工)剩余3.4 km到达指定贯通里程位置(预计贯通里程DIK403+650)，钻爆法施工进口段剩余800 m到达指定贯通里程位置(预计贯通里程DIK403+650)。为保证隧道准确贯通，选择最优位置，利用高精度陀螺仪进行洞内导线定向测量。

2.2 磁悬浮陀螺全站仪

高精度磁悬浮陀螺全站仪是利用磁悬浮支撑技术使仪器的灵敏部处于悬浮状态，在地球角动量的作用下产生指向力矩

M=H×ωecosφsinα

(8)

式中，α为陀螺马达轴与子午线北方向的夹角[7]。

在指向力矩的影响下，力矩器会产生一个与其大小相等方向相反的作用力，此时可计算出陀螺马达轴的北向偏角[8]，其大小为

(9)

可利用在常数边标定的仪器常数与测站点子午线收敛角计算坐标方位角(子午线收敛角由测站点概略坐标求得)[9]。

2.3 陀螺方位测量的必要性

(1)西秦岭隧道地面施工控制网由GPS构网，本身有良好的观测和检核条件，对贯通误差的影响较小[10]。控制贯通误差的关键是洞内导线的测量精度，隧道内距离洞口最远的导线点为最弱点。随着导线测量的不断推进，误差不断累积且缺乏检核条件。因此，可以通过加测高精度陀螺边的方法增强洞内导线的精度。

(2)隧洞内注浆紧跟盾构机，既有控制点基本上不受施工影响，但局部地段因管片开裂等原因，对既有控制点产生一定程度影响，这有可能给后期的导线测量带来粗差。因此，有必要通过陀螺定向的方法对隧道内导线进行检查。

(3)隧道内因通视条件较差，高温高湿度状态下的折光、照准等因素会使隧道内光电导线精度受到影响，甚至可能存在粗差。因此，有必要通过陀螺定向的方法对隧道内导线进行检查，以提高隧道内导线精度。

(4)随着工程施工技术不断发展，对测量技术要求越来越高。目前，在长大隧道方面还缺乏新测量技术的应用实践。秦岭隧道属于全国铁路第二长隧道，有必要利用有效的测量方法对西秦岭隧道内光电导线进行检验，为今后深埋超长隧道的测量技术积累经验。

2.4 加测陀螺边方案设计

如图4所示，选左侧两条常数边GD1→CPI154、GD1→GD2来测定仪器常数；并用右侧已知边GZ3→GZ2进行检核，分别对隧道洞内以贯通面为中心小里程方向的三条导线边及大里程方向两条导线边进行高精度陀螺定向测量。

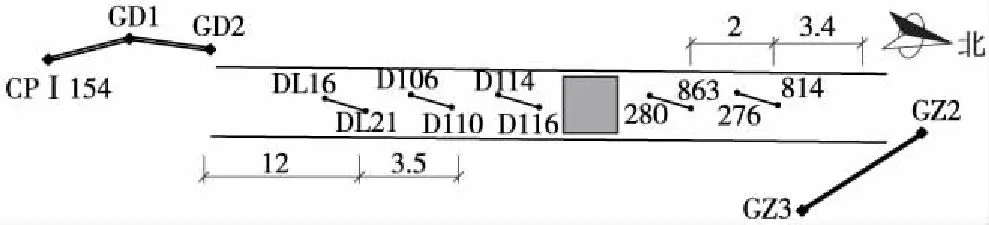
图4 常数边与定向边示意(单位：km)

为满足隧道的设计贯通精度，本次磁悬浮陀螺定向测量精度应优于±3″，根据已有的陀螺定向测量作业流程，参照相关规范及质量要求，并根据长大隧道洞内导线测量的实际情况，观测流程作如下调整：

(1)首先对洞外选取的两条常数边分别进行定向测量，对标定的仪器常数进行检核，并与全站仪测量的∠GD2-GD1-CPI154夹角值进行比较，可直观反映出陀螺定向的可靠性，保证仪器常数稳定准确[11]。

(2)对隧道内的4条定向边先进行两个测回的陀螺观测，然后在导线的另一端架设仪器对向观测两个测回[12]。这里仅对第5条定向边D114→D116进行两测回独立陀螺定向测量。

(3)为保证在地面测定的仪器常数同样适用于地下，洞内陀螺定向完成后应立即返回地面，重新对常数边进行反方向测量，以保证仪器常数的稳定性。

为进一步验证仪器常数的可靠性，本次选择隧道出口处的常数边GZ3→GZ2作为检核。

2.5 加测陀螺边贯通误差预计

根据现场实际情况及洞内环境状况，本次选用的仪器测角中误差为2″，测边中误差为±(1+1D)mm，陀螺标称精度3.5″。在此基础上，利用贯通测量误差公式进行推算，可对隧道洞内施测陀螺边前、后进行贯通误差预计，本项目允许误差应小于160 mm。

依据隧道洞内导线测量设计图，并参照选用的仪器参数，可预计隧道贯通误差值，导线测量与加测陀螺边的隧道贯通误差预计值见表1。

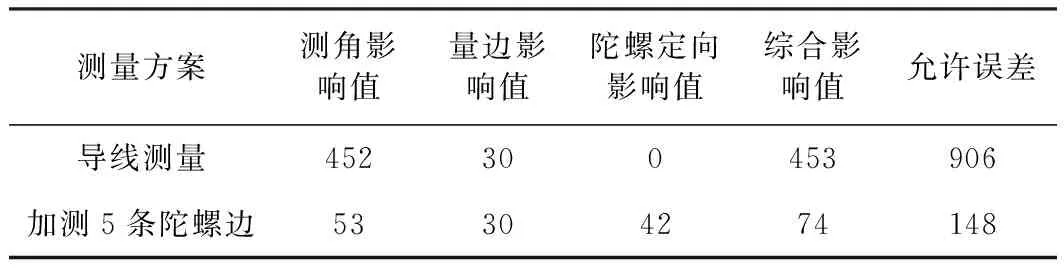
表1 施测陀螺定向边前后贯通误差预计 mm

由表1可知，未加测陀螺边时，推算出的贯通误差较大，大于设计贯通精度；而隧道洞内加测一定数量的陀螺边后能够有效控制贯通误差，达到设计要求。

3 贯通成果及精度分析

3.1 陀螺定向稳定性分析

陀螺定向一般进行两测回或三测回测量，得到导线两次或三次的陀螺方位角差值[13]，据此便可计算陀螺定向中误差，如表2所示。

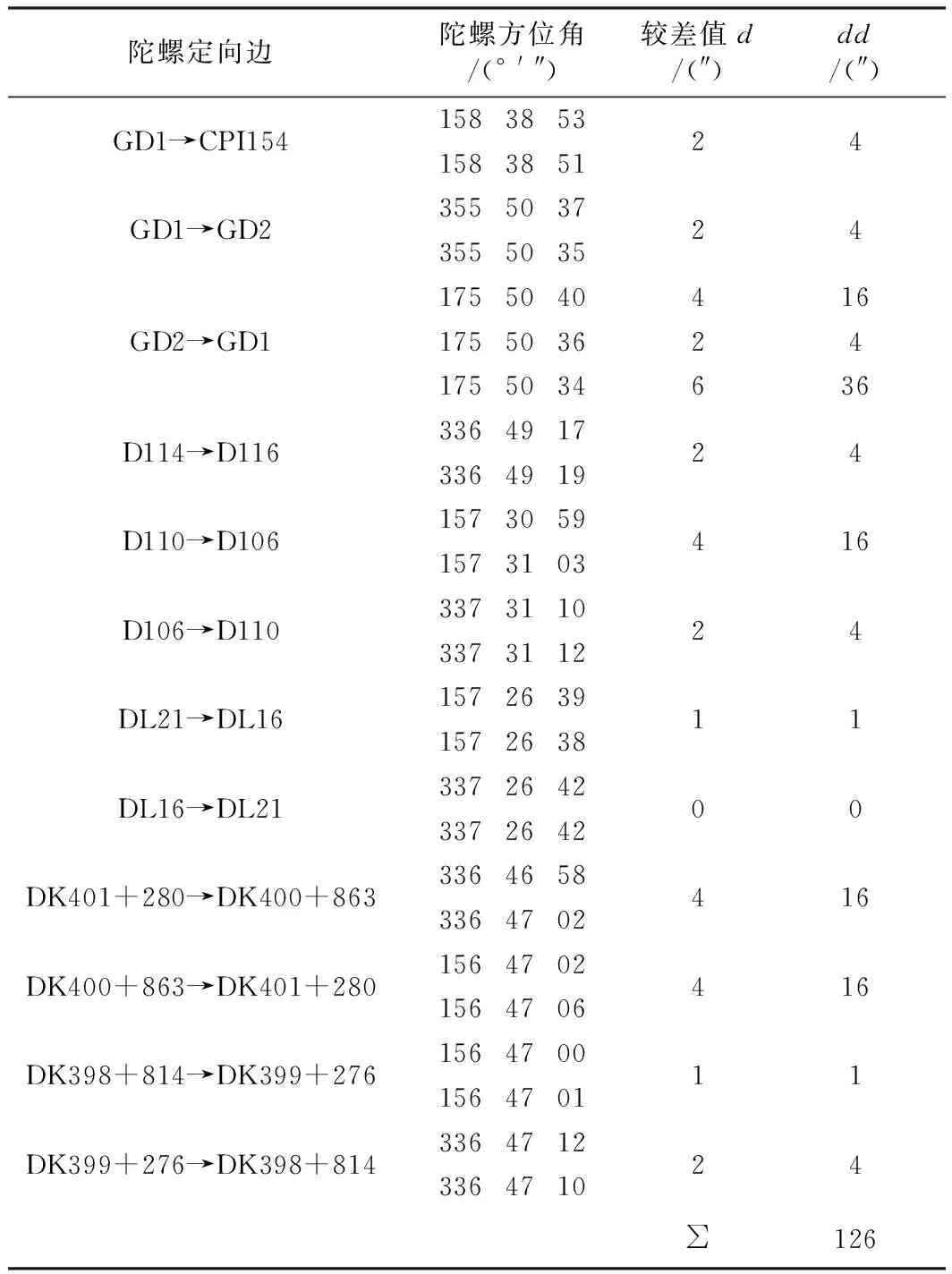
表2 多观测列陀螺定向精度计算

本次陀螺定向中误差为

洞内导线边定向精度为

其中N、nΔ、n分别为双观测列个数、仪器常数测回数、洞内定向边测回数[14]。隧道内导线边陀螺定向测量后，可利用在常数边标定的仪器常数与测站点子午线收敛角计算坐标方位角，再与导线实测的方位角进行对比，如表3所示。

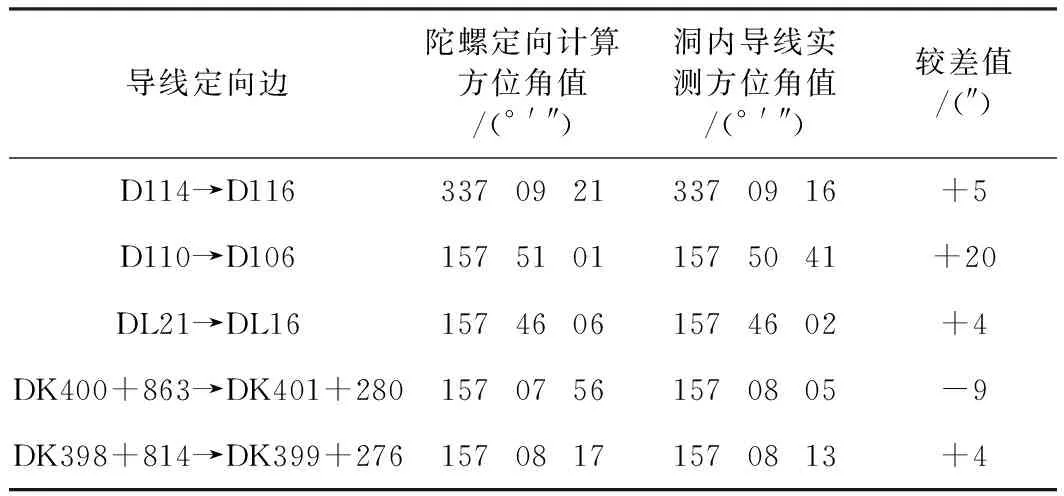
表3 陀螺定向与导线实测坐标方位角对比

据此可绘制洞内导线方位修正示意(如图5)。

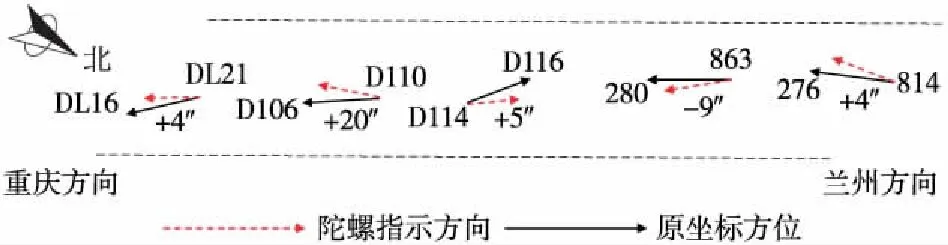
图5 陀螺定向边校正方位示意

本次观测量条件良好，陀螺定向成果稳定可靠[15]。导线成果与陀螺定向方位符合较好，仅D110→D106导线边偏差较大，而该条边已距离进口15km，导线系统误差是引起长距离方位偏差大的根本原因。可参照本次陀螺定向方位，对洞内导线边D110→D106进行修正。

3.2 贯通测量成果

共计测量西秦岭隧道导线点266个，设计洞内最优位置陀螺定向边5条。对于隧道洞内导线测量，横向贯通误差是评定贯通测量质量的主要指标，本次仅统计导线平面测量精度，如表4所示。

表4 导线测量平面精度统计

3.3 贯通测量精度分析

隧道洞内陀螺定向测量后，依据陀螺测定的方位角值，对洞内导线的方位予以适当修正。本次西秦岭超长铁路隧道横向贯通误差为0.071 m，远小于贯通允许误差(0.16 m)，贯通精度优良。

4 结论

该项目研究的核心是长大铁路隧道贯通测量中陀螺定向边最优位置的选择及数量的确定，并据此来制定隧道贯通测量方案。可按照设计方案进行误差预计，若是计算出的贯通误差不能满足工程要求，应及时调整陀螺定向方案，重新进行贯通预计，直至满足设计要求。

在隧道贯通测量过程中应严格保证测量精度并对测量数据进行精度评定[16]，保证贯通测量顺利实施。