核电厂主回路耦合分支管道的地震分析研究
2019-05-27卢强陈星文
卢强,陈星文
(上海核工程研究设计院有限公司,上海 200233)
0 引言
反应堆冷却剂系统主要由压力容器、蒸汽发生器、主泵、主管道及主设备支撑等构成,是保证核电站一回路压力边界完整的核心系统,对整个核电站的安全有效运行起着至关重要的作用。核电站反应堆冷却剂回路系统模型涉及的设计输入参数复杂,运行工况繁多,计算数据量庞大。同时,反应堆冷却剂回路的力学分析为蒸汽发生器、蒸汽发生器支撑、压力容器、压力容器支撑、主泵及主管道的最终评定提供重要的设计输入。因此,为了确保整个核电厂寿命期内安全有效运行,保证反应堆冷却剂主回路的力学分析模型及方法的准确性具有重要的意义。
美国核管会标准审查大纲[1-2]指出,在进行抗震分析时,主结构要考虑子结构的影响。对于反应堆主冷却剂系统,其边界条件复杂,连接了众多的分支管道,根据分支管道连接的支撑系统,可以分为直接与主管道相连和间接与主管道相连两大类。直接与主管道相连的大管径管道主要有波动管、非能动余热排出管道和正常余热排出管道等管道。间接与主管道相连的主要包括与蒸汽发生器相连的主蒸汽和主给水管线,与压力容器相连的直接注射管线。对于间接与主管道连接的分支管道类型,目前解耦问题并未形成明确的准则。主回路系统整体采用了柔性支撑的设计,对于相对于主管道尺寸较大、连接位置在蒸汽发生器上部的管道,需要进行其对主管道地震分析的影响研究。
通过对电站主冷却剂系统与分支管道的地震耦合分析进行理论论证,为了进行后续数值分析研究打下基础。通过进行主回路系统与蒸汽发生器分支管道耦合模型的地震分析,评估此类分支管的标高和管径对主管道分析影响。根据评估结果为核电厂设计分析提供具有参考意义的指导,同时为其他大型分支管的耦合影响论证提供参考,最终为建立此类型分支管道的解耦准则打下基础。
1 耦合分析理论论证
为了论证分支管对反应堆冷却剂回路计算的影响,就要对耦合分支管后的反应堆冷却剂回路模型设定正确的边界条件。
根据结构动力学,模型的动力学计算方程如公式(1)所示:

式中:K为结构的刚度矩阵,Δ为结构的位移矩阵,C为结构的阻尼矩阵,M为结构的质量矩阵,F为结构所受到的外载矩阵。
首先对结构的刚度矩阵进行相关的计算[3]。设主模型共有n个自由度,则主模型的刚度矩阵如式(2)所示:
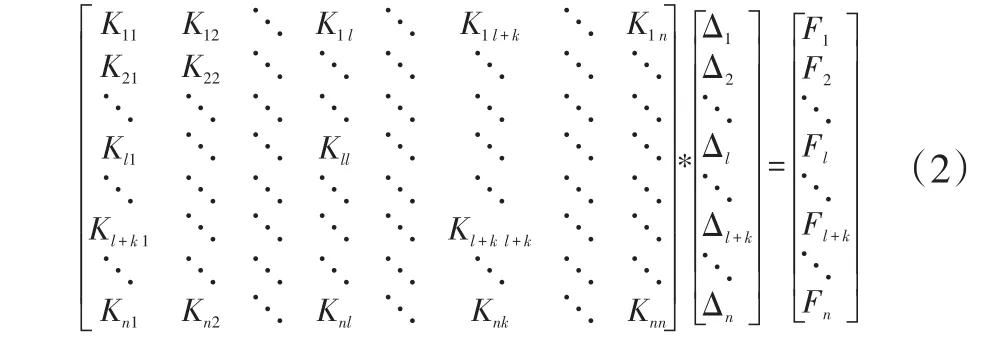
式中,刚度矩阵元素Kij为J方向自由度的单位位移在i方向自由度所产生的载荷。刚度矩阵元素Kl1至Klk为将要解耦的节点的自由度。
解耦点施加位移的子模型的刚度矩阵如公式(3)所示,由于从主模型中删除掉了一些单元和节点,因此,假设其共有n-m个自由度。

上式中的刚度矩阵元素与主模型中的刚度矩阵元素唯一的不同的是至。其代表的是解耦点的刚度矩阵元素。
Δl至Δl+k为解耦点的节点位移,在Δl至Δl+k相等的前提下,需论证公式(2)和公式(3)能够求得相同的解。
对公式(1)进行相应的推导计算,整体刚度矩阵中删掉不包含在子模型的自由度,得到公式(4)的刚度矩阵方程。
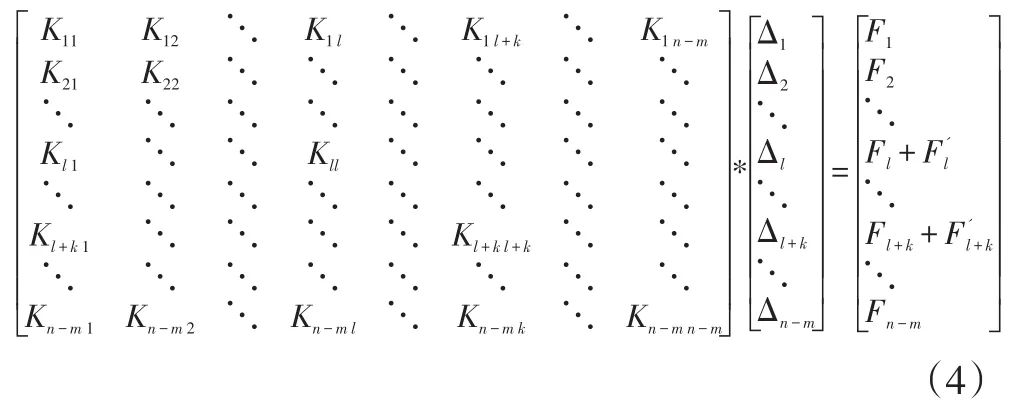
其他的系数与公式(2)完全相同。
Klr至Kl+ks为与解耦自由度相连,但不在子模型中的自由度在解耦点的刚度矩阵元素。
删掉公式(4)中的L至K行,再将刚度矩阵中的L至K列移到公式的右边,可得公式(5)的刚度方程。

对子模型的刚度矩阵采用同样的计算方案,即删掉公式(3)中的L至K行,再将刚度矩阵中的L至K列移到公式的右边,同样可得公式(5)的刚度方程。
对于公式(5)中各个矩阵的意义,阐述如下:
(1)方程左边的第1部分为子模型中,除解耦点外的所有自由度的刚度矩阵,此部份矩阵,对于子模型与主模型是相同的。
(2)方程左边的第2部分为子模型需求解的节点自由度位移。
(3)方程右边的第1部分为子模型中,除解耦点外各个自由度接点上所承受的外载荷,此部分矩阵子模型与主模型相同。
(4)方程右边的第2部分为解耦点自由度对子模型中其他自由度的刚度矩阵元素,由于在解耦点赋予了同样的边界条件,所以此部分矩阵也不变。
(5)方程右边的第3部分为解耦点自由度的位移,即解耦点处施加的边界条件,此部分内容从主模型中提取,施加在子模型上,所以子模型与主模型中此部分内容相同。
因此,对于方程式(5)中的各矩阵,子模型和主模型中的元素完全相同,主模型和子模型也必然求得相同的结果。
根据上述的理论推算,可以得到如下结论:若要进行主模型与子模型的耦合影响分析论证,必须保证子模型中的单元与主模型的单元施加同样的边界条件和载荷,方能求得合理准确的结果。即若要进行分支管道对反应堆冷却剂回路的地震分析影响论证计算时,必须对反应堆冷却剂回路和分支管施加相同的,协调一致的地震时程。
2 分析输入
2. 1 地震时程输入
为了得到分支管道支撑根部的地震时程输入,首先建立主回路和分支管道ANSYS模型,然后添加到厂房模型中并与厂房结构耦联,如图1所示。对厂房模型施加地震载荷,得到主系统和分支管道支撑根部的位移时程输入。地震载荷分别考虑了软土和硬基岩的地基条件,每种地基条件又分别考虑了设计值刚度、刚度下限值和刚度上限值三种情况,如表1所示。

图1 主回路和分支管道与厂房耦联
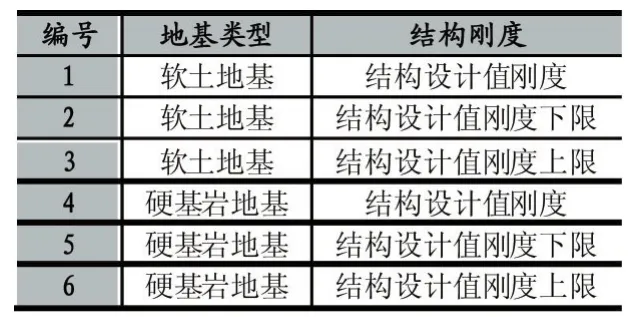
表1 地震时程信息
2. 2 地震时程输入
根据规范RG 1.61的要求主回路的地震分析时应当采用4%的临界阻尼。由于主回路地震模型考虑了支撑非线性的影响,需采用直接积分时程分析方法计算,而直接积分法只能通过瑞利阻尼系数添加等效阻尼。
瑞利阻尼的结构阻尼阵如下式所示:

其中,M为质量矩阵,K为刚度矩阵,α和β分别为质量阻尼系数和刚度阻尼系数。临界阻尼ξ确定的情况下,根据计算目标的起始频率ω1和截止频率ω2可求得阻尼系数,关系表达式如下:


3 地震分析研究
3. 1 频率分析
由于模型的地震分析是采用的瑞利阻尼添加结构阻尼的,需要对耦合模型进行模态分析,根据规范要求确定地震分析所采用的瑞利阻尼系数。基于主回路模型,分别对耦合和不耦合分支管道的主回路模型进行模态分析,对比模态分析的计算结果。
表2显示了耦合DN650、接管标高位于蒸发器上部支撑处的分支管道模型后主回路模型主要频率相对于未耦合模型的差异,从表中可以看出,两组模型计算得出的各阶模态的频率非常接近,频率差异在千分之一的级别,影响可以忽略不计。
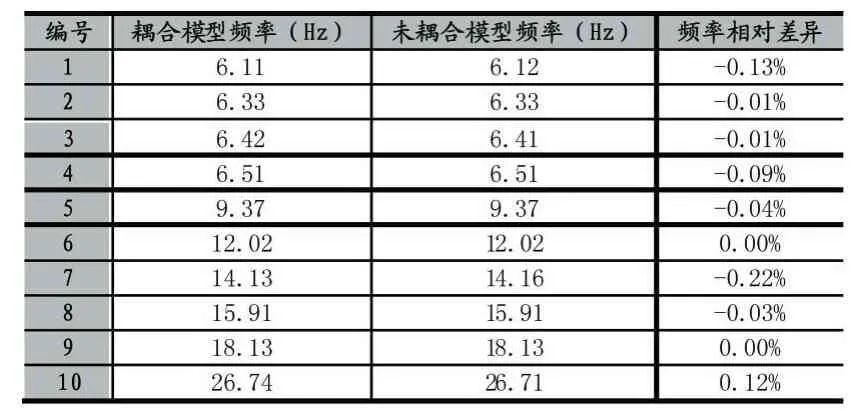
表2 主要频率对比
图2-图4分别显示了两组模型三个正交方向的第一阶主频的振型情况。根据两组模型三个正交方向的第一阶主频的振型情况可知,耦合DN650分支管道对主回路的振型影响较小。
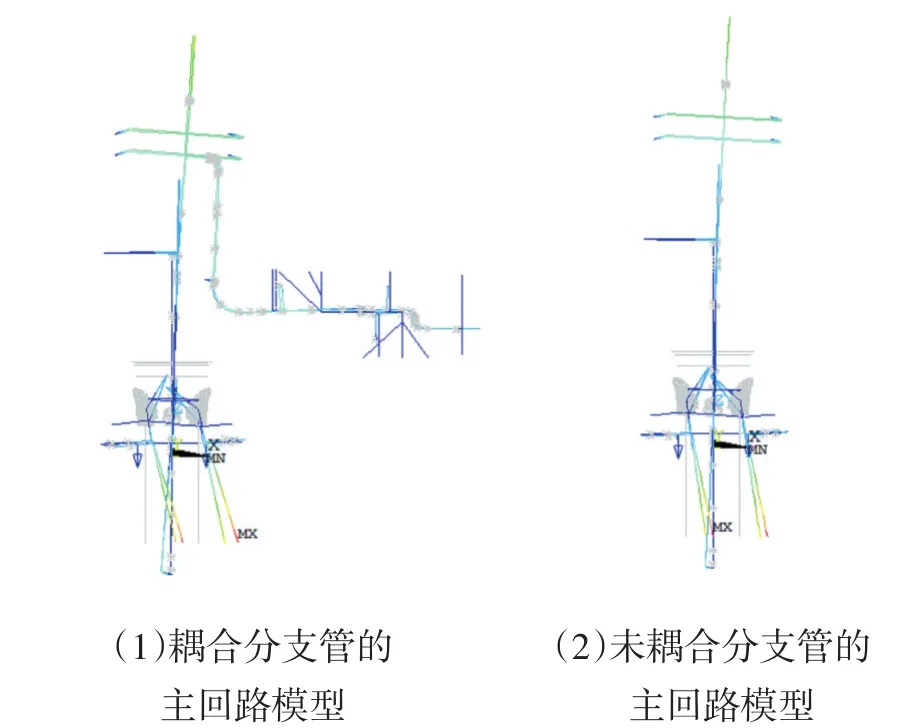
图2 X向第一阶主频振型
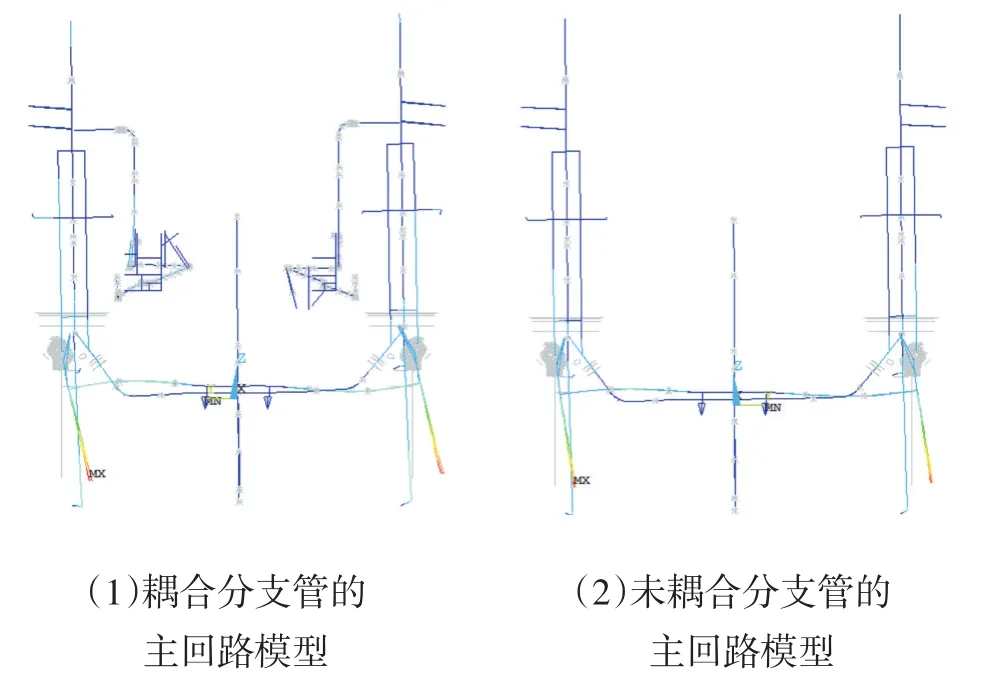
图3 Y向第一阶主频振型

图4 Z向第一阶主频振型
3. 2 分支管道管嘴标高影响
考虑到与主管道相对位置及主回路支撑系统的影响,通常认为分支管道标高越高,对底部主管道的影响会随标高的升高而增大。假设分支管道的管嘴标高相对于蒸汽发生器逐渐升高,得到主管道热段和冷段单元合力距影响如图5所示,对主设备支撑载荷的影响如图6所示。随着分支管嘴标高的升高,无论是主管道单元还是主设备支撑载荷,影响都有增大的趋势。从对分析结果影响的量来看,主回路各项分析结果对分支管道管嘴标高是不敏感的。
3. 3 分支管道管径影响
保持分支管道壁厚不变的情况下,假设分支管道的管径逐渐增大,得到主管道热段和冷段单元合力距影响如图7,对主设备支撑载荷的影响如图8所示。随着分支管径的增大,分支管道对主管道单元载荷和主设备支撑载荷的影响有增大的趋势;分支管径增大对于主管道热段单元载荷的影响要大于对冷段的影响;对于主设备支撑载荷,随着分支管道管径增大,对蒸汽发生器的中部和上部支撑的载荷具有显著影响。当分支管道管径低于DN750时,对主管道各项指标的影响较小。当分支管道管径增大到DN1050时,主管道热段末端单元的载荷与蒸汽发生器中部和上部支撑载荷有明显的增大。

图5 管嘴标高对主管道单元载荷的影响

图6 管嘴标高对主设备支撑载荷的影响
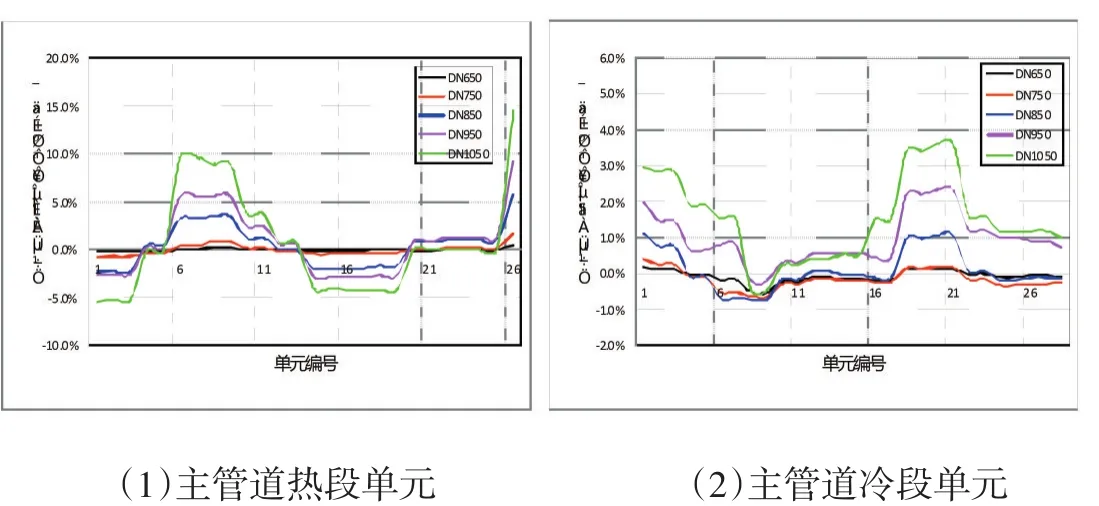
图7 管径对主管道单元载荷的影响
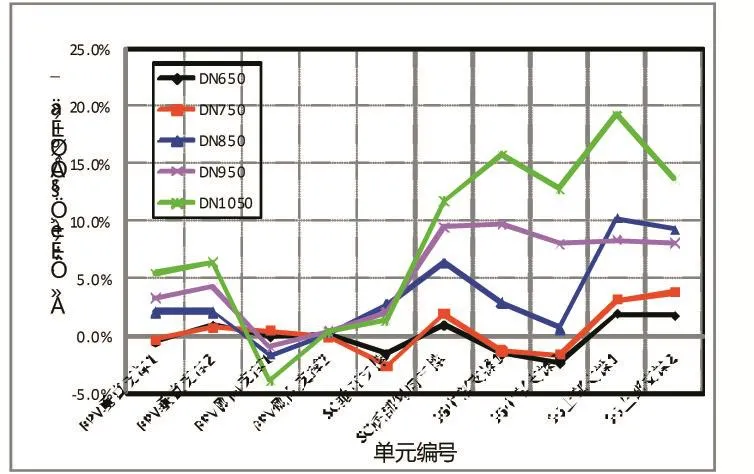
图8 管径对主设备支撑载荷的影响
4 结语
通过动力学结构理论研究,建立了耦合分支管道对主回路计算影响的分析方法。根据这套方法,进行了蒸汽发生器分支管道标高和管径对主回路地震分析影响的研究,对于与蒸汽发生器相连的分支管道,其管嘴标高对主回路地震分析的影响很小;分支管道的管径对主回路分析结果的影响敏感,当管径增大到一定程度时,对主回路分析结果具有显著影响。
通过以上的分析结论,对主回路地震分析模型边界确定提供了有价值的参考,并最终为该类分支管道解耦准则的建立打下了基础。
