结合膜计算与人工蜂群算法的K均值算法

黄文成

（西华大学计算机与软件工程学院，成都 610039）

0 引言

聚类是一种重要的无监督学习技术，其目标是将数据集合分成若干簇，使得同一簇内的样本相似度尽可能大，而不同簇间的样本相似度尽可能小，目前该技术在机器学习、模式识别、Web挖掘以及图像量化等领域得到了广泛的应用[14]。

K均值（K-means）算法是解决聚类问题的经典算法之一。但由于K均值聚类算法敏感于初始值和易受孤立点影响,容易陷入局部最优,并且全局搜索能力较弱,这些致命点严重影响聚类的性能[16]。为解决函数优化问题，由Karaboga于2005年提出了人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[12,13]，该算法是一种模拟生物群体智能的优化方法，具有实现简单、参数数量较少、全局搜索能力好、鲁棒性强等多种优点。但ABC算法还是存在收敛速度较慢、较容易陷入局部最优等问题。

近年，研究人员考虑到两种算法有许多互补之处，着手研究将两种算法进行结合。李海洋等人[17]提出IABC-K算法，将ABC算法和K-means算法进行合理切换，应用于图像分割。曹永春等人[18]提出IABCC算法，使用ABC算法和K-means算法对数据进行交替迭代。喻金平等人[3]提出IABC-Kmeans算法，使用ABC算法和K-means算法在对数据进行交替迭代的同时，并对适应度函数及初始值的获取进行了改良。Janani等人[19]提出ABC-BK算法及新的适应度函数，并将此算法应用于文本聚类。Alam等人[20]提出WDC-KABC算法应用于网页文献聚类。Cong等人[21]提出EABCK算法，将K-means算法应用于由ABC算法得到的全局最优值的再次寻优。Giuliano等人[22]提出ABCk算法，将K-means算法嵌入到ABC算法的雇佣蜂和观察蜂阶段，加快算法收敛速度。Bonab等人[23]提出CCIAABC-K算法，应用于对数据的聚类和图像的分割。这些混合算法大多克服了K-means算法对初始值敏感，ABC算法收敛速度慢的问题。但是，初始值的选取还是对混合算法的结果有影响，也存在着容易陷入局部最优,求解精度和算法不太稳定的问题。

鉴于以上的问题，本文将膜计算（Membrane Computing，MC）[24]的概念组合到 K-means和ABC的混合算法中，提出一种结合膜计算与人工蜂群算法的K均值算法（K-means algorithm:Combining P system with Artificial Bee Colony Algorithm，PABC-K）来优化聚类问题。

1 准备知识

1. 1 K均值算法

K均值算法因其简单性和易于实现而被广泛使用。K均值算法根据参数K将给定数据集聚类为K个簇，以每个数据点到其聚类中心的距离平方和为目标函数,通过求解函数极小值方式反复迭代,直到目标函数收敛。

K均值聚类目标函数为：

K均值聚类中心迭代公式为：

其中，N为数据样本数；K为聚类中心数；Xj为第j个数据点；Ci为第i个聚类中心；wji为权重，当第j个数据点属于第i个聚类中心时，其值为1，如不属于，则为0。

1. 2 ABC算法

ABC算法通过模拟蜂群分工合作寻找最优蜜源的过程求解优化问题，是一种基于蜜蜂群体智能的优化算法[1]。ABC算法具有控制参数少、易于实现等优点，在函数优化方面具有比较好的表现。在ABC算法中，蜜蜂被分为雇佣蜂、观察蜂和侦查蜂这3类。食物源的位置表示一个可行解，每个食物源只对应一只雇佣蜂，即雇佣蜂的数量等于食物源的数量。观察蜂的数量则设置为和雇佣蜂相同。ABC算法的基本步骤如下：

步骤1：种群的初始化。设具有n个样本点的数据集X={xi∈Rd,i=1,2,…,n},xi为d维向量；设算法的最大迭代次数为MCN，每个蜜源的最大开采次数为limit，蜜源个数为SN。

步骤2：根据如下公式（3）随机选择蜜源，作为初始可行解：

其中，j∈{1,2,…,d}；Xij表示第 i个蜜源的第 j维分量；Lj表示所有样本中第j维的数值下限；Uj表示所有样本中第j维的数值上限。

步骤3：雇佣蜂根据公式（4）在当前蜜源的邻域范围内更新蜜源。运用贪婪选择法，比较新旧解的适应度，保留质量好的解：

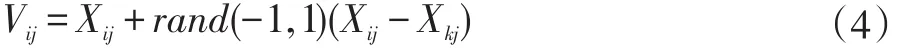
其中，i,k∈{1,2,…,SN}，且i≠k。

步骤4：每个雇佣蜂更新蜜源后，观察蜂选择一只雇佣蜂，跟随其前往蜜源采蜜。观察蜂选择雇佣蜂的概率计算公式如式（5）所示：

其中，fi为第i个蜜源的适应度值。观察蜂通过公式（5）选着比较好的蜜源，随后根据公式（4）再次更新蜜源。

步骤5：某蜜源的搜索次数达到最大开采次数Limit,但蜜源适应度不再变化时,放弃该蜜源。同时,将雇佣蜂转换为侦察蜂。侦察蜂根据公式（3）搜寻新的蜜源，以代替被放弃的蜜源。

步骤6：判断是否达到最大迭代次数达或满足循环终止条件。若是,算法结束并输出适应度最好的蜜源作为最优解。若不是,返回步骤3。

1. 3 膜计算

膜计算又称为P系统，是罗马尼亚科学院院士Gheorghe Paun于1998年11月基于细胞膜结构提出的一种自然计算方法[2]。Nishida[4]在2004年将膜计算引入到遗传算法中，第一次提出了膜优化算法的概念。膜计算还被引入到了粒子群算法[5]、人工鱼群算法[6]及K-medoids[7]、KNN[8]等算法中。膜优化算法已成为了膜计算领域中的一个重要分支。同时，P系统也被大量应用于图像分割方向[9-11],并且获得了比较好的结果。

P系统具有分布式、极大并行性和非确定性的特点。根据膜结构的特点，P系统可以分为细胞型P系统、组织型P系统和神经型P系统。其中细胞型P系统是其他两种P系统的基础[2]。细胞型P系统的基本结构如图1所示。最外层的细胞膜（1号膜）称为表层膜，它分隔开外部环境和内部空间；膜内部没有其他膜存在的细胞膜，被称为基本膜（2、4、5号膜）。在P系统中，各个膜的空间中可以具有各自不同的对象和运算规则。

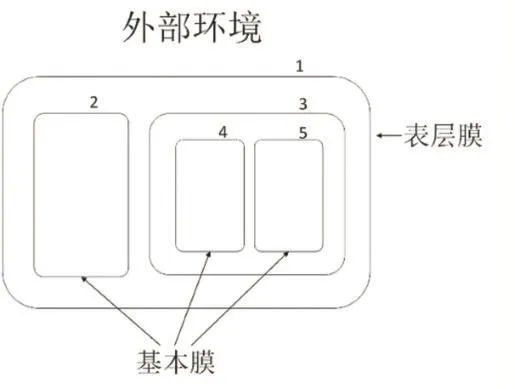
图1 细胞型P系统的结构

形式上，一个细胞型P系统定义如下：

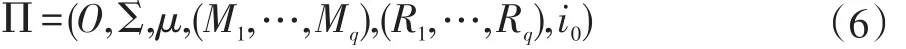
其中：O是对象的有限字母表；Σ⊂O是输入字母表；μ是由q个膜组成的膜结构，q称为P系统Π的度数；Mi（1≤i≤q）表示q个膜中各自包含的对象；Ri（1≤i≤q）表示q个膜中各自包含的规则；i0∈{0,1,2,…,q}是系统Π的输出膜。

规则Ri是二元组（u,v），通常写成u→v,u是字母表O中的字符串,v是O×{here,out,in}上的一个字符串。其 中，v具 有（a,tar）的 形 式，其中a∈O,tar∈{here,out,in}。如果tar=here，则a位于规则所在的区域中；如果tar=out，则a被传送到规则所在的区域的高一级区域中；如果tar=in，则a被传送到规则所在的区域的低一级区域中。

2 PABC-K算法

2. 1 最大最小距离积法初始化

无论K均值算法还是人工蜂群算法都对初始值敏感,而随机的初始化影响着算法的收敛速度和最优解的质量。文献[3]针对最大最小距离法和最大距离积法的不足，提出最大最小距离积法来对初始值进行初始化，以解决初始点过于密集等问题。

算法流程图如图2所示。其中，D是包含所有数据的集合；k是要选取的初始点个数；Z是存储k个初始点的集合，算法开始前为空集；Temp是存储Z中各元素到D中各元素的距离的数组。

该算法所需参数少；可以选取到点密度较大的点，稀疏了初始点的分布；通过乘积法放大了点与点之间的差异，选取过程更具区分度。

2. 2 膜系统结构

PABC-K算法建立在细胞型P系统的基础上，采用单层膜结构，如图3所示。0号膜为表层膜，分隔开外部环境和内部空间。表层膜内部具有n个细胞膜，全部都为基本膜。基本膜之间可以相互交流，基本膜和表层膜也可以相互交流。

图2 最大最小距离积算法流程图

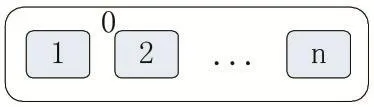
图3 单层膜结构

PABC-K算法中，多种群蜂群与P系统结合，每个基本膜中存在一个蜂群，表层膜中不包含蜂群。在每次的迭代过程中，每个基本膜中的信息通过表层膜进行交互，每个基本膜中的蜂群相互间不产生影响。表层空间能够获取各基本膜渗透出来的局部最优食物源，通过贪婪选择法，选出全局最优食物源。表层膜空间将全局最优食物源，分别渗透回每个基本膜中，用以影响各基本膜中下一次进行的迭代。

该P系统的定义如下：

（1）Π =(O,μ,(M0,...,Mn),R,i0)

（2）O是整个样本集

（3）膜结构包含n个细胞膜，具体结构μ=[[]1,[]2,[]3,...,[]n]0，其中0表示表层膜。

（4）初始种群的分布为：

M0=φ1=O,M2=O,…,Mn=O

其中，M0为皮肤膜的初始集，是一个空集。Mi（1≤i≤n）为每个基本膜，包含对象都为整个样本集。

（5）输出字母表io表示表层膜的输出，也是PABC-K算法的最终输出，表示一组食物源。

细胞膜空间中的规则：

（1）每个基本膜中都独立运行K-means算法与ABC算法的混合算法；表层膜空间内进行贪婪选择法的进化规则。

（2）各基本膜将各自运算出的最优的食物源发送至表层膜；表层膜则将最终得到的最优的个体复制n份发送回各基本膜。

2. 3 结合膜计算与人工蜂群算法的K均值算法

在PABC-K算法中，以膜系统作为总体框架，结合人工蜂群算法来优化K-means算法的聚类中心，用以对数据进行聚类运算。本算法设计了一个细胞型P系统，它是一个带有进化规则和转运规则的P系统，使用单层膜结构，具有一个表层膜和n个基本膜。每个基本膜中都有进化规则和多个对象，并且每个对象都与表层膜之间有转运规则。由ABC算法和K-means算法相结合的混合算法作为每个基本膜中的进化算法，作用于将要进行聚类的数据。各基本膜与表层膜间运用转运规则，将各基本膜中得到的局部最优解转运到表层膜空间中，并接收表层膜空间得到的目前状态的全局最优解，转运回各基本膜空间中。表层膜中将使用贪婪选择法作为进化规则，作用于从各基本膜得到的局部最优解，得到全局最优解，并运用转运规则传回各基本膜中。

每个基本膜中，都存在着一个蜂群，单独运行由ABC算法和K-means算法相结合的混合算法，寻找最优食物源。食物源个数设置为k，每个食物源代表一个聚类中心点；设置最大迭代次数MCN。

在混合算法中，使用前文介绍的最大最小距离积法对食物源进行初始化，得到适应度较好的初始食物源。在雇佣蜂阶段，使用K-means算法来加强局部寻优能力，同时加快对目标函数的收敛速度。由于K-means算法的快速收敛，对局部最优值能较准确的搜寻，在雇佣蜂阶段就能将所有食物源的局部最优值寻出。在ABC算法中，观察蜂主要作用于优质食物源，起到加快收敛的作用；而在本算法中，由于K-means算法的作用，在雇佣蜂阶段就已将所有食物源的适应度函数收敛，替代了观察蜂的作用，故在本算法中将雇佣蜂阶段省去。通过表层膜得到的全局最优值将作用于侦查蜂阶段，侦查蜂阶段主要是将食物源更新，避免整体算法陷入局部最优值；将全局最优值加入到食物源的更新过程，加强了食物源更新的目的性，有利于整体算法收敛速度的加快。

PABC-K算法的总体流程图如图4所示。

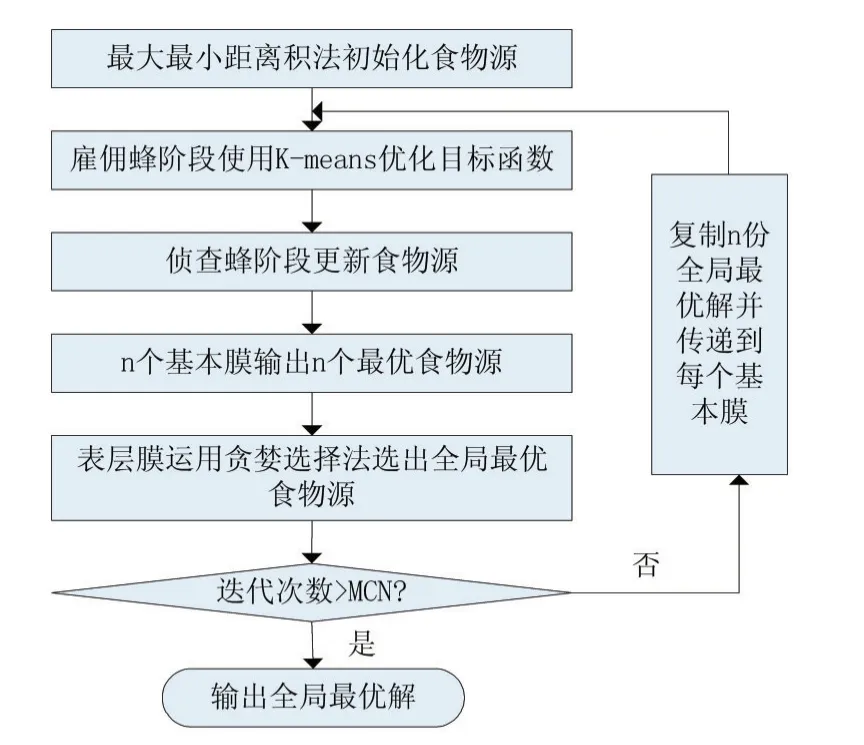
图4 PABC-K算法流程图

3 实验结果与分析

为了验证本文中PABC-K算法进行聚类的有效性，从UCI数据集中选取4组真实数据集进行试验。对每组数据集，分别用K-means算法、人工蜂群（ABC）算法、文献[25]中提出的ABC算法的改进算法（Cooperative ABC,CABC算法）、文献[22]中提出的融合了ABC算法和K-means算法的ABCk算法以及本文提出的结合膜计算与人工蜂群算法的K均值算法（PABC-K算法）进行算法聚类，并对结果进行比较分析。

4组测试数据集分别为UCI数据集中的Wine、Iris、CMC以及Glass数据集。

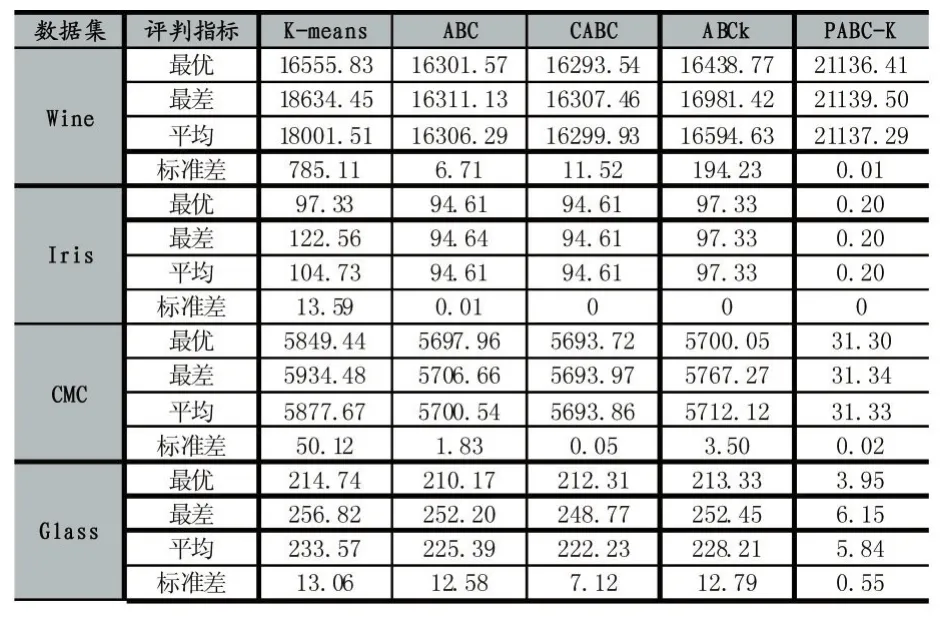
表1 各算法簇间距离的比较

对于每个数据集，每个算法单独运行20次。表1显示了通过20次实验，各算法适应度的最优值，最差值，平均值以及标准差。适应度如1.1小节中公式（1）所示，数值越小，代表聚类效果越好。

由表1中数据可以看出：K-means算法的标准差较大，对初始值具有敏感性，容易陷入局部最优，稳定性偏差。ABC算法、ABCk算法、CABC算法都对数据集具有较好的聚类效果，与K-means算法相比具有较大的提高，稳定性提高也比较大。ABCk算法是ABC算法和K-means算法的结合算法，可以看出其聚类效果要略差于ABC算法和CABC算法，这是由于K-means算法对初始值敏感的缺点对该结合算法产生了影响，但是ABCk算法克服了ABC算法收敛缓慢的缺点。本文提出的PABC-K算法对聚类也取得了比较好的结果，在4个数据集上得到的标准差都十分低，该算法的稳定性十分好，能很好的摆脱对初始值的敏感；同时，由于K-means算法的加入，大大加快了本算法的收敛速度。

除了在Wine数据集上的聚类结果比其余4种算法的聚类效果稍差外，在Iris数据集、CMC数据集和Glass数据集上，都取得了很好的聚类效果。经过分析，Wine数据集中的样本某一维的数据值远远大于其余维数上的数据值，在通过欧式距离进行聚类时，该维的数据对聚类的结果产生了严重的影响，掩盖了其余维数上数值间的差别。虽然该算法对数据集具有比较好的聚类效果，但是正确分类的准确率却不是太高。在Iris数据集上取得了约90%的准确率，但是在其余3个数据集上获得的准确率并不高。这个也再次说明基于欧氏距离进行的聚类有一定的限制性，并不能适用于所有的数据集。

4 结语

本文根据ABC算法、K-means算法和膜计算这3种算法的优点和缺点，在膜计算的框架下，以ABC算法为基础结合K-means算法，提出了PABC-K算法。以最大最小距离积法初始化蜜源，K-means算法嵌入到雇佣蜂阶段加快算法收敛速度，膜计算作为整体框架涉及整个算法的各阶段。算法通过在4个公开的标准数据集上运行，验证了其具有较好的聚类效果和较高的稳定性。根据实验中算法产生的结果以及相应的分析，进一步的研究将着重于对数据的预处理（如归一化预处理等）和算法目标函数的改进。