Mathematical rules for synergistic,additive,and antagonistic effects of multi-drug combinations and their application in research and development of combinatorial drugs and special medical food combinations
2019-05-26ShoujunYuanHaoyuChen
Shoujun Yuan,Haoyu Chen
a Beijing Institute of Radiation Medicine,Academy of Military Medical Sciences(AMMS),Beijing 100850,China
b Beijing Brightshines Technology Co.Ltd.,China
Keywords:
ABSTRACT
1. Introduction
The research and development of new drugs have tended to adopt a single target–single drug model,which involves the selection of an appropriate drug target,screening a series of candidates,evaluating their druggability, and then performing pre-clinical evaluations and clinical trials for each candidate in turn, before they can be approved by the pharmaceutical regulative authority for market listing. However, the etiology of many serious diseases like cancers, cardiovascular–cerebrovascular diseases, and metabolic diseases are related to many targets,and patients often derive less benefit from single-target drug therapy [1]. Therefore,for greater effectiveness, it is often necessary to direct drugs at multiple targets.
To solve this problem, combined drugs or new combinatorial drugs can be a better choice for relieving a complex disease.Also,the research and development of recipes for special medical foods can not only play an auxiliary role,but a more central role in daily health care.In traditional Chinese medicine,combinations of various drugs derived from animals,plants,and minerals are frequently used as both medicine and food,or as a fixed prescription.
The purpose of applying multi-drug (or multi-component)combinations is to obtain the greatest therapeutic benefit while minimizing toxic side effects. Since multi-drug and multicomponent combinations interact at multiple levels,the final effect may be synergistic,additive,or antagonistic.If a multi-component combination is not scientifically and precisely evaluated, patients can face great therapeutic and toxic risks due to drug interactions.

Fig.1. Schematic diagram of Rule 1.(a) and (b): On the basis of the pharmacodynamic line value of drug B (i.e., g (Bn)), drug A advances the pharmacodynamic increment of the Am dose along its own doseresponse curve,namely Yexp =Y(Am +Bn).(c)and(d):On the basis of the pharmacodynamic level of drug A(i.e.,f(Am)),drug B advances the pharmacodynamic increment of the Bn dose along its own dose-response curve,namely Yexp =Y(Bn +Am).
In this paper, we present mathematical rules regarding the synergy,addition,and antagonism of a multi-drug combination discovered in our laboratory [2]. By establishing mathematical rules in a“one-belt,one-line model”,we offer real examples of the quantitative calculation of the synergies, additions, and antagonisms produced by the combined application of multiple components.This model can be used to scientifically and accurately determine the synergistic, additive, and antagonistic effects and the corresponding dosage ranges of combination drugs and special medical foods during their research and development and it lays a solid theoretical and experimental foundation for their successful market listing.
2. Mathematical rules for synergy,addition,and antagonism of multi-drug combinations
To clarify the mathematical rules of the synergistic, additive,and antagonistic effects of a multi-drug combination,the expected additive effects of a multi-drug combination should be defined first.Then, by comparing the actual observed effect with the expected additive effect, we can determine the synergistic, additive, and antagonistic effects of the multi-drug combination. These effects have two aspects:mathematical rules regarding the expected additive effects of a multi-drug combination and definitions of its synergistic,additive,and antagonistic effects.
2.1. Description of mathematical rules of expected additive effect of multi-drug combination
Consider that drugs A and B have the same target pharmacodynamic value Y, and their dose–effect relationship functions are Y=f (x) and Y=g (x), respectively. When the dose of drug A is Am,its pharmacodynamic value is Y=f (Am); when the dose of drug B is Bn,its pharmacodynamic value is Y=g(Bn).When Amand Bnare combined,the expected additive efficacy value(Yexp)is not Yexp=f(Am)+g(Bn).Rather,we describe the resulting Rules 1 and 2 in the following:
Rule 1:The expected additive effect value of a two-drug combination can be considered to be the efficacy value of one drug,with the other drug following its own dose–effect curve to reach an efficacy increment value for its own dose, and vice versa, as shown schematically in Fig.1.

Fig.2. Schematic diagram of Rule 2.
Due to the different action modes of drugs A and B, their expected additive effect value(Yexp)is characterized as Y(Am+Bn) /=Y (Bn+Am). Essentially, the expected additive effect is sequentially additive and can be expressed as follows in formula group(1):

Note: Yexp: Expected additive effect; g(Bn): Pharmacodynamic value of drug B at dose Bn; f(Am)|g(Bn): On the basis of the pharmacodynamic level of drug B (g (Bn)), drug A advances the pharmacodynamic increment of the Amdose along its own dose-response curve. f(Am): The efficacy of drug A at dose Am;g(Bn)|f(Am): On the basis of the pharmacodynamic level of drug A(f(Am)),drug B follows its own dose-response curve and advances the pharmacodynamic increment of the Bndose.
Rule 2:For any dose combination of two drugs(e.g.,Amand Bn),the expected additive effect value comprises a value domain with continuous characteristics, and its boundary values are Y(Am+Bn) and Y (Bn+Am), respectively, which is a closed interval number set. In a two-dimensional coordinate diagram, the dose–relationship of the expected additive pharmacodynamics is a belt or a curved band,which is a number set function of the closed interval.
The actual observed dose–effect relationship of the two-drug combination is a curve,as shown in Fig.2.
For any single-dose combination(Am,Bn),the expected additive effect comprises a value domain with continuous characteristics,as shown by the red vertical line segment on the coordinate graph on the left. By connecting all the endpoints of the line segments of the expected additive effects for all dose combinations,a belt area between the two curves is generated in the coordinate graph,which we call a dose–effect belt, as shown in red on the right. The black curve is the actual observed dose–effect curve of the combined dose.
The formula for constructing dose–effect curves for the expected additive effects is as follows.

Note:Square brackets[]denote closed interval symbols.
By substituting formula group(1)into formula(2),we obtain a general formula(3)for calculating the expected additive effect,as follows:
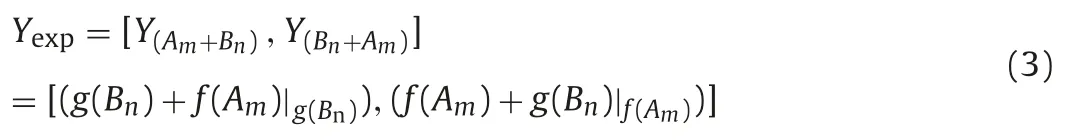
Expansion of the expected additive rule: When multiple drugs are used together (N ≧3), the expected additive effect value is based on the efficacy value(s)of one drug(or one drug group), with the other drug (or drug group) following its own dose–effect curve (or dose–effect belt) to reach the efficacy increment value(s)of its own dose(or dose combination).Therefore, the dose-response belt of the expected additive effect in a three or more drug combination is composed of multiple curves.
2.2. Definitions of synergy,addition,and antagonism in multidrug combinations
According to the above mathematical rules for the expected additive effect of multi-drug combinations, the dose–effect relationship of the expected additive effect of a drug combination constitutes a dose–effect belt. In this way, the definitions of synergy, addition, and antagonism can be clearly defined. Therefore,synergy is defined as the actual observed efficacy being greater than the value domain range of the expected additive effect,addition is the actual observed efficacy within the value domain range of the expected additive effect, and antagonism is the actual observed efficacy being less than the value domain range of the expected additive effect.The deduction and proof process of the mathematical rules for the expected additive effect of multiple drugs are detailed in the literature[3].
3. Quantitative calculation of parameters of synergistic,additive,and antagonistic effects of multi-drug combinations
3.1. Dose range of synergy,addition,and antagonism
A comparison of the actual observed dose–effect curve (or the actual value of the observed drug effect) with the expected dose–effect belt shows that the dose range of the synergy is located along the actual observed dose–effect curve above the expected additive dose–effect belt; the dose range of the addition is within the expected additive dose–effect belt that overlaps the actual observed dose–effect curve; and the antagonistic dose range is located below the expected additive dose–effect belt. The dosage range of the synergistic, additive, and antagonistic effects can be quantitatively calculated in graphical measurements along the“one belt,one line”in the two-dimensional coordinate graph,or by calculating the equation groups derived from the actual dose–effectcurve equation and the curve equation of the expected additive dose–effect belt.

Table 1 Effects of Cur combined with CT1042 on the growth of subcutaneous xenograft tumors of NCI-H460 cells in nude mice.
3.2. Combination index based on dose,CId
At a certain combined dose level, we can compare the actual observed pharmacodynamic value (Yobs) with the two boundary values for the domain of the expected additive effect, that is, the maximum and minimum values in the range of the expected additive effect, Yexp-max and Yexp-min, to obtain CId1and CId2. We do so using the following formula group(4):

Judgment criteria:Synergy:CId1>1,CId2>1;Addition:CId1≦1≦CId2;Antagonism:CId1<1,CId2<1.
4. Research examples
The above mathematical derivations and verification process are conducted in accordance with the common dose–effect range of a multi-drug combination of each single drug. The functions described in this paper are all incremental. Here, we provide the following two examples:1)an evaluation of the combined efficacy of one food ingredient and one medicine; 2) an evaluation of the combined efficacy of extracts from a variety of medicinal and edible plants.
4.1. Example 1:evaluation of the anticancer effect of curcumin combined with CT1042 on xenograft tumors of NCI-H460 non-small-cell lung cancer in nude mice
CT-1042 is a new type of camptothecin derivative,whose main action mechanism is the activation of the P53 protein,promotion of Bax activity,inhibition of the expressions of Bcl-2 and Survivin,and induction of the apoptosis of cancer cells.The anti-cancer activity of CT-1042 is strong and is also characterized by serious toxicity[4].Curcumin(Cur),a yellow pigment extracted from the rhizomes of the edible plants Curcumaceae and Araceae, has many biological activities, including being anti-inflammatory, anti-oxidative,and anti-tumor[5].In this paper,we demonstrate the quantitative evaluation of the synergistic, additive, and antagonistic effects of a combination of these two drugs on the anticancer activities of NCI-H460 in vivo.
Although the derivation and proof of the mathematical rules for the expected additive effects are more complicated[6],in practical application, the calculation process is not difficult to understand.The key is to transform different combination doses into additive equivalent doses, and then compute the numerical range of the expected additive effects for each drug’s respective function equation in the dose–effect relationship.
The potent anticancer effects of a combination of Cur and CT1042 can be observed on xenograft tumors of human lung cancer NCI-H460 cells in nude mice,the main endpoint results(inhibition rate on tumor weight)of which are summarized in Table 1.
4.1.1. Calculation procedures
Step 1 Generate dose–effect relationship tables of each drug and their combinations and fit the respective dose–effect relationship curves and equations.
Table 1 shows the main endpoint pharmacodynamic data for the single and fixed ratio (1:500) combination of CT1042 and Cur on the inhibition of NCI-H460 xenograft tumors,i.e.,the inhibition rate on tumor weight.We observed no significant difference in the toxicity indices(survival rate and body weight).
According to the distribution of the dose and effect values in the two-dimensional graph,curves and functions of single drugs of CT1042 and Cur can be well fitted with an appropriate regression model.
1) The dose–effect relationship curve and function for single CT1042
Using the ExpDec1 model in MicroGal Origin software,we generated a fitting curve of the dose–effect relationship for CT1042,as shown in Fig.3A, and derived the function equation, as shown in Eq.(1)below.
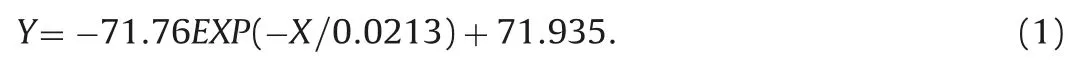

The equation is also denoted as Y=g(x).
3) Dose–effect relationship curve and function for the combination of CT1042 and Cur Using the linear regression model in MicroGal Origin software, we generated a fitting curve of the dose–effect relationship,as shown in Fig.3C,and derived the function equation,as shown in Eq.(3)below.

The equation is also denoted as Y=h(x).
Step 2 Take the equivalent dose exchange based on the dose–effect relationship equation at the same situation and sequentially calculate the expected additive effect values in a multi-drug combination according to Rules 1 and 2. Then, calculate the combination index based on the actual dose levels(CId1,CId2).

Fig.3. Dose–effect relationship curve for single and combined uses of CT1042 and Cur.

Table 2 Calculated expected additive effects and combination index for combination of CT1042 and Cur after sequential equivalent doses exchange.
In the genral formula(3)above,the doses of CT1042 in combination as a reference drug are denoted as Am, the doses of Cur in combination as a reference drug are denoted as Bn,and their corresponding equivalent doses are respectively expressed as Bmand An.We can calculate the expected additive effect values derived from CT1042 as a reference drug by the function expression f(Am+An).The expected additive effect values derived from Cur as a reference drug are determined using the function equation g(Bm+Bn).Table 2 summarizes the expected additive effect values for CId1and CId2.
The two combinations of CT1042+Cur in Table 2, combination groups 1 and 2,are synergistic(CId1>1,CId2>1).
Step 3 Generate a dose–effect belt in the two-dimensional coordinate system.The abscissa represents smaller dose scales for the combination.The ordinate represents the expected additive effect values at certain dose levels of the combination.Based on the abscissa and ordinate, fit the dose–effect curve equations that constitute the boundaries of the expected additive dose–effect belt.
According to Table 2,the dose scales 0.0025 mg/kg+1.25 mg/kg(CT1042+Cur)are set between two dose combinations of CT1042+Cur (given the need for accuracy in the calculation, other scales can be set).Then,the expected additive effect values are calculated using the equations in Table 2 and the calculated values of the actual observed effects are obtained using Eq.(3):Y=h(x).Fig.3D shows a schematic of the one-belt,one-line result(as the calculation process is similar to that in Table 2,it is omitted here).

Fig.4. Diagram of the effect of several extract combinations of medicinal and edible plants.
As shown in Fig.3D,the dose–effect belt of the expected additive effect of the two medicines is toothbrush-like in shape.The actual effect values of both groups are located above the expected additive dosage-effect belt,which means they are synergistic.Since the actual dose–effect curve of the combined group does not cross the expected additive dose–effect belt,we naturally omitted the calculation of the dosage range of the synergic,additive,and antagonistic effects.Based on these results,we suggest that there are synergistic effects in the range of available combination doses.
4.1.2. Evaluation
Under the current administration conditions, the combination of the two groups showed a synergistic effect.Based on these experimental results, we can conclude that it is helpful to choose a combination regimen of CT1042 and curcumin.
4.2. Example 2:evaluation of several extract combinations from
medicinal and edible plants,such as raspberry,mulberry,ginseng,wolfberry,burdock,blueberry,etc.,on the exhaustion test results of weight-bearing swimming in mice.There are many optional indicators for this study,but the most critical is that of swimming exhaustion in weight-bearing mice
In the above study,all the combined elements have an effect on the end point target,so the pharmacodynamics change after their combination, and the process of quantitative evaluation becomes more complex,which is typical of drug combinations.However,in the combination of plant extracts, members are often ineffective when used alone, whereas when used in combination, they often show efficacy, which has caused some confusion in past evaluations.It is relatively simple to apply the one-belt,one-line model for an evaluation. In this model, each member alone is invalid,having the mathematical function formula is Y=f (x)=0, which coincides with the X-axis in the two-dimensional coordinate system. The dose–effect relationship of the expected additive effect in the combined group is also Y=g(x)=0.If the combined group is effective,it will be shown as the actual effect curve Y=h(x)>0.By calculating,we can obtain CId=+∞.
In this case,we used four combinations to evaluate their effects on swimming exhaustion in mice, including combination 1 (raspberry powder,ginseng extract,burdock extract,RGB),combination 2 (raspberry powder, mulberry extract, burdock extract, RMB),combination 3 (raspberry powder, blueberry powder, wolfberry extract, RBW), and so on. In previous studies, these combination doses were ineffective in all single-member applications.As such,when combined,the expected additive effect should also be invalid,that is, the expected additive effect value should also be Yexp=0.Also,the CIdof the combination for RGB and RBW is+∞.
Fig.4 shows the actual test results and the calculation results using the one-belt, one-line model. A graphical analysis indicates that the combinations can produce a synergistic effect. The RGB combination has a strong synergistic effect,whereas the RBW combination has only a weak synergistic effect.
杂志排行
食品科学与人类健康(英文)的其它文章
- Diet and medical foods in Parkinson’s disease
- Functional food products in Japan:A review
- Biting force and tongue muscle strength as useful indicators for eating and swallowing capability assessment among elderly patients
- Influence of luteolin on the apoptosis of esophageal cancer Eca109 cells and its mechanism of action
- A value-added cooking process to improve the quality of soybean:Protecting its isoflavones and antioxidant activity
- Chemical constituents,biological functions and pharmacological effects for comprehensive utilization of Eucommia ulmoides Oliver
