动力载荷与外压联合作用下深海管道的压溃

2019-05-25134蒋梅荣134

中国海洋平台 2019年1期

134 蒋梅荣134

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300072；2.高新船舶与深海开发装备协同创新中心，上海 200240；3.中海油研究总院, 北京 100028； 4.海洋石油工程股份有限公司, 天津 300451)

0 引言

由于海底地形复杂，受海流冲刷、温度变化等影响，管道在深海条件下易出现局部悬跨。悬跨管线除了受内外压作用外，还受水流的升力、拖曳力等动力载荷作用,此部分动力载荷目前主要作为正弦载荷进行研究;同时，深海管道易受地震和化学爆炸的影响，地震波可以简化成一系列正弦波和余弦波的叠加[1]，外物化学爆炸、海底火山爆发等对管道的载荷作用则可以近似为余弦函数的形式[2]。因此，研究在压力与动力载荷联合作用下，尤其是在外压与正弦载荷、余弦载荷联合作用下，局部椭圆度管道的强度问题,具有很大的工程意义。

在管道压溃屈曲和动力响应的相关领域，国内外专家学者在理论模型、数值模拟、试验验证等方面研究成果丰富。早在1913年，SOUTHWELL[3]提出管道弹性屈曲的相关理论并进行试验验证；之后在大量管道压溃试验的基础上，KYRIAKIDES等[4]基于屈曲大变形分析中结构几何非线性和材料非线性的考虑，开发相应的数值计算方法； TOSCANO等[5]应用ADINA软件进行管道的屈曲压溃过程模拟，突破薄壳理论的限制，提高厚壁管道屈曲临界值求解的精度；余建星等[6-7]利用自主研制的深海压力舱，进行全尺寸管道压溃试验，研究径厚比、初始凹坑缺陷、初始椭圆度等因素对压溃的影响；赵保磊[8]进行无阻尼条件下单向动力加载与静压联合作用对管道压溃影响的数值模拟。

迄今为止，关于管道压溃的研究主要集中在不同形式的静力载荷的联合作用，而关于管道的动力特性，则大多只是考虑管道所受的梁振动影响而忽略了局部缺陷对壳振动的影响或直接忽略阻尼对管道壳振动的影响。少数关于动力载荷的研究也直接假定输入的动力载荷满足正弦形式。实际上，深海管道所受动力载荷作用可以简化成正弦载荷和余弦载荷两大类。余弦载荷和正弦载荷对管道结构压溃影响的区别在于:初始时刻余弦载荷的冲量大，易造成结构破坏;当作用时间有限时，两者塑性蠕变的差异会造成低周循环破坏性质的差异等。本文以带有局部椭圆度缺陷的钢管为例，应用ABAQUS软件对管件在阻尼条件下受压力和动力载荷联合作用的情况进行数值模拟，比较正弦载荷和余弦载荷对管道结构压溃影响的差异，并对相关因素进行敏感性分析，可以作为管道结构安全的参考。

1 理论分析

管道的振动主要分为梁振动和壳振动,根据振型叠加法的理论,在动力载荷的激励下,管道的梁振动和壳振动总是同时发生的。动力载荷对管道压溃的影响主要通过两个路径实现；第1条路径是梁振动引发的管道轴向截面之间相对位移产生的弯矩影响；第2条路径是壳振动直接引发的管道截面的变形趋势影响。

图1 薄壁圆柱壳自由度示例

结构在交变载荷作用下，易出现棘轮效应，即结构塑性应变不断累积直至结构破坏。棘轮效应是工程中须重点考虑的因素，其常常在低周循环中出现，会减小结构的疲劳寿命或使结构发生大变形从而不能正常工作。深海环境属于高压环境，高压会对棘轮效应产生放大作用[9]。由于棘轮变形是一种二次变形累积，要准确地预测材料或结构的棘轮效应非常困难，目前主要结合数值模拟对棘轮效应的相关影响作进一步研究。

将管道视为薄壁圆柱壳进行简化处理，如图1所示，其中：R为内径；u、w、v分别为轴向x、径向z和环向θ的位移。针对薄壁圆柱壳采用Kirchhoff-Love假定，即：

(1) 变形前垂直于中面的直线在变形后仍然是直线，与变形后的中面保持垂直，且长度不变，也称直法线假设；

(2) 垂直于中面方向的应力与其他应力相比可忽略不计。

对于壁厚为h、长度为L的圆柱壳，壳上一点坐标由轴向x、径向z和环向θ等3个方向坐标轴定义。由于梁振动方向仅发生小变形，根据小变形假定，管道轴向仅考虑应力而忽略应变和位移。

用w(x,θ,t)、v(x,θ,t)表示管道的中性面上任意一点在任意时刻的径向和环向位移，其中t为开始发生位移所经历的时间。整个管道的质点位移如下：

w(x,θ,t,z)=w(x,θ,t)

(1)

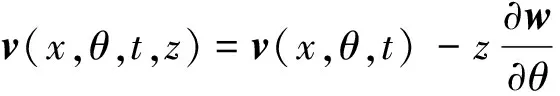
(2)

管道环向的格林应变张量可表示为

(3)

考虑管道屈曲过程中的大变形，本构关系采用J2塑性流动理论。

通过最小加速度法可将管道承受动载的真实加速度响应从可能加速度响应中区分出来,从而得到关于管道位移、速度和加速度的一系列微分方程。将管道承受外压和动力载荷的情况代入一般形式的Lee泛函中，得到

已知某时刻tq的加速度，通过迭代法可求得下一时刻的位移和速度，特定管道外压条件下在管道表面施加某一幅值余弦载荷，通过反复迭代得到不同时刻的管道质点位移。若在某一时刻后管道关键点(一般为内壁短轴上的点)位移不再增大，则认为管道不发生压溃，继续增大余弦载荷幅值直至得到临界压溃面载荷幅值。

2 数值模拟

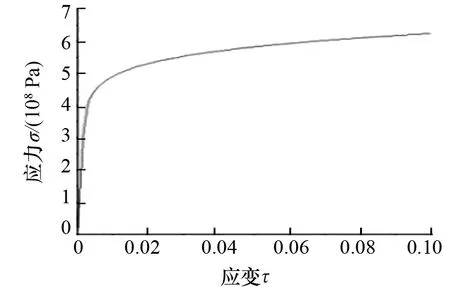
图2 钢材应力-应变曲线图

图3 模型示例

2.1 模型建立

计算模型选用材料模拟APIX65钢材,输入的材料参数为：密度7 850 kg/m3,弹性模量2×1011Pa,泊松比0.3,并输入如图2所示的应力-应变关系。

悬跨管件全长为10 m，外径为0.325 m，两端固支。为了减小计算量，从管跨中间进行截断并在ABAQUS中建立半管模型。半管模型全长为5 m，一端固支，从固支端开始至轴向4.5 m段为全圆截面，管件截面从轴向4.5 m开始从全圆渐变为椭圆度为3%的椭圆截面，并在椭圆度为3%的截面处建立边界条件限制其轴向运动，如图3所示。为克服剪切自锁效应，选用C3D8I单元。在划分网格时对椭圆度变化部分进行局部加密。

模型的计算分为两个部分：

(1) 通过riks算法求得管件在静压作用下的临界压溃压力。对管件外表面施加大小为100 MPa的静压，得到对应的LPF曲线，并求得管道的临界压溃压力为9.805 MPa。

(2) 首先通过static分析步给管件模型外表面施加9.5 MPa的外压，然后通过dynamic implicit分析步给管件外表面施加圆频率为10 rad/s的余弦载荷，初始载荷方向为短轴(y轴)正向，载荷大小为2×104Pa，由于地震作用时间一般在30 s内，爆炸载荷作用时间更短，设定载荷作用时间为30 s，并观察管件的压溃情况。通过管件的压溃情况不断调整载荷大小，直至得到符合设定精度要求的临界动力面载荷幅值。同样，将余弦载荷调整为正弦载荷，进行正弦载荷的模型计算。

2.2 模型验证

(1) 动力验证

直梁弯曲振动的梁函数可表示为

Φ(x)=B1sin(μx)+B2cos(μx)+B3sh(μx)+B4ch(μx)

(5)

式中：B1、B2、B3、B4及μ为待求参数；μ为与结构自由振动频率λ有关的参数。

μ的计算式为

ch(μl)cos(μl)=1

(6)

代入两端固支的边界条件，可得到结构自由振动频率λ的表达式为

(7)

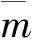
(2) 静压验证

通过压力舱对局部椭圆度为7%的API-X65钢材(325 mm×10 mm)进行多组压溃试验，得到管道的临界压溃压力为7.6 MPa；对ABAQUS中局部椭圆度为7%的管道模型通过riks算法求临界压溃压力，得到模型的临界压溃压力为7.71 MPa：与试验数值的误差仅为1.4%。因此，用ABAQUS来处理动载和外压联合作用下的管道压溃问题是合理的。

图4 模型压溃过程图

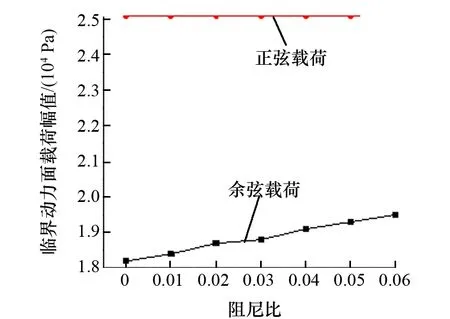
图5 不同阻尼下临界动力面载荷幅值

2.3 计算结果

通过不断调整载荷幅值进行模型计算：当施加的余弦面载荷幅值达1.81×104Pa时，管道不发生压溃；而当施加的余弦面载荷幅值达1.82×104Pa时，管道发生压溃。因此，在限定的条件下，管道的余弦面载荷临界压溃动力幅值为1.82×104Pa。压溃过程如图4所示。

在实际工程中，管道在动力载荷作用下会受到阻尼的影响，因此需讨论阻尼对管道在静压和动力载荷共同作用下管道压溃的影响。图5为在不同阻尼比状态下正弦载荷和余弦载荷分别作用下的临界动力面载荷幅值，可知阻尼比对临界正弦面载荷幅值的影响在限定的精度内可以忽略，对临界余弦面载荷幅值影响较大。随着阻尼比的上升，临界余弦面载荷幅值基本呈线性上升趋势。在不同阻尼比状态下，正弦载荷作用下的临界面载荷幅值均大于余弦载荷作用下的动力面载荷幅值，原因在于余弦载荷在作用开始阶段的冲量较大，易造成结构破坏。综上所述，选定准确的阻尼比对之后的研究意义重大。

根据DNV规范[10]，管道总阻尼ξ是结构阻尼ξstr、土壤阻尼ξsoil和水动力阻尼ξh等3部分之和,其中：结构阻尼ξstr主要取决于管道的材料属性，如无特殊说明，钢制管道一般取ξstr=0.005。由于研究的是悬跨管段,因此不考虑土壤阻尼的影响。水动力阻尼ξh随着管道振动速率等因素时刻发生变化,求解复杂，此处采用经验公式的方法。

先计算流体阻尼系数rh

rh=γΩρeD2

(8)

式中：系数γ=CD/(4πSt)，CD为拖曳力系数，St为斯特洛哈尔数；漩涡脱落频率Ω=2πStU/D，U为结构与流体间的相对速度；管外海水密度ρe=1 024 kg/m3；管道外径D=0.325 m；式中St可被约去，因此只需得到速度和拖曳力系数，即可得到流体阻尼系数。

再计算水动力阻尼ξh

(9)

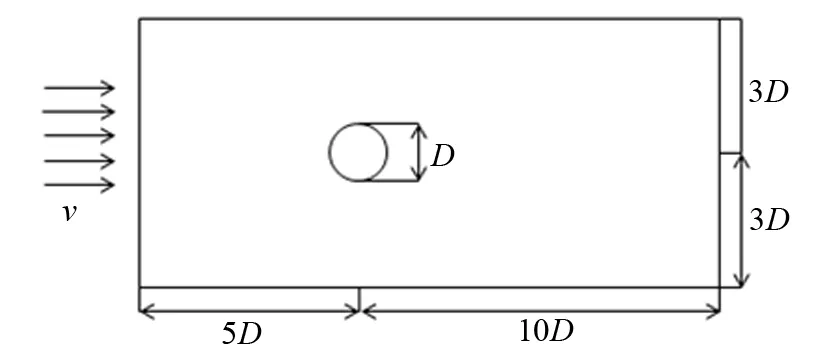
图6 二维模拟无限流场中的管道

式中：计算得到单位长度的管道质量me=77.68 kg/m；通过ABAQUS中frequency分析步得到模型的一阶固有频率ω1=125 rad/s。

在低约化速度、低雷诺数的情况下，可以在Fluent软件中将管道截面作为固壁处理求得拖曳力系数CD[11]，如图6所示，其中：v为入流速度；D为管道直径。

设定入流速度为1 m/s,管道在无限流场中所受阻力因数取阻力曲线稳定后的均值0.287。计算得水动力阻尼为0.002 5。考虑实际情况，认为管道下方存在海床，近壁条件对拖曳力具有放大作用[11]，取水动力阻尼为0.005。

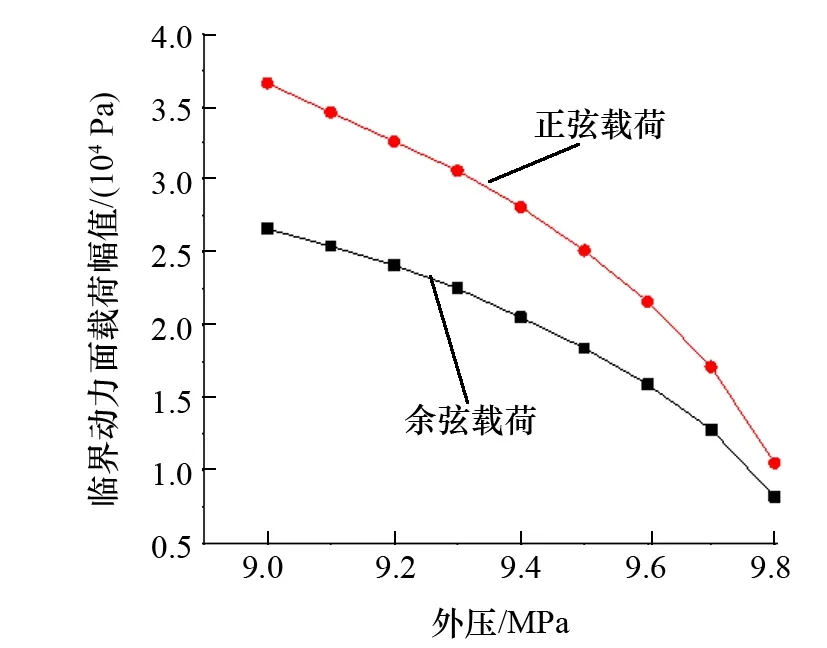
图7 不同外部压力下临界动力面载荷幅值

由计算模型的假定和计算，可得计算模型总阻尼

ξ=ξstr+ξsoil+ξh=0.005+0+0.005=0.010

(10)

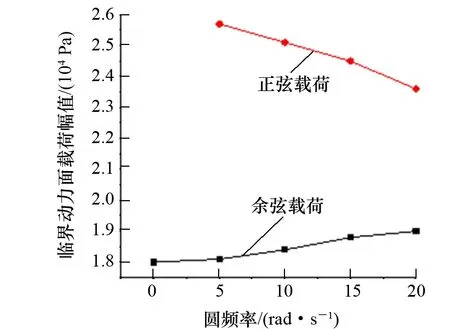
图8 不同圆频率下临界动力面载荷幅值

将总阻尼0.010通过瑞利阻尼的方式等效施加在管道模型上，得到改进的管道模型。在之后的数值模拟中采用改进后的管道模型。

3 敏感性分析

3.1 外部压力

采用局部椭圆度为3%、阻尼比为0.010的管道模型。改变外部压力大小，并沿管道短轴(y轴)方向在管道外表面分别施加圆频率为10 rad/s的正弦载荷和余弦载荷，得到如图7所示的临界动力面载荷幅值曲线。

从图7可知：随着外部压力的增大，在正弦载荷和余弦载荷作用下的临界面载荷幅值均呈下降趋势，且该下降趋势随着外压的增大而增大。当外压为9 MPa时，正弦载荷的临界动力面载荷幅值远大于余弦载荷的对应幅值，随着外压增大，两种载荷的临界面载荷幅值均逐渐缩小，两种载荷的临界面载荷幅值之差逐渐缩小。

3.2 圆频率变化

采用局部椭圆度为3%、阻尼比为0.010的管道模型。在管道外表面施加9.5 MPa压力，并沿短轴(y轴)方向在管道外表面分别施加不同圆频率的正弦载荷和余弦载荷，得到如图8所示的临界动力面载荷幅值曲线。

由于深海水流速度较小，管道的泄涡频率多在0～20 rad/s，就此区间的圆频率变化进行研究，并计算圆频率为管道一阶振动频率即125 rad/s时的情况作为比较。

正弦载荷在圆频率为0 rad/s时无载荷输入，因此不予讨论。从图8可知：在圆频率为0～20 rad/s内，正弦载荷的临界面载荷幅值随圆频率上升而下降，而余弦载荷的临界面载荷幅值随圆频率上升而上升。这说明在指定频率区间内，正弦载荷和余弦载荷对圆频率上升的响应不同，在工程中必须注意。当圆频率为125 rad/s时，正弦载荷输入时的临界面载荷幅值为6 700 Pa，余弦载荷输入时的临界面载荷幅值为8 200 Pa。相较低频区间，两种载荷的临界面载荷幅值均大幅减小，说明共振对管道局部压溃的危害性很大，在工程中需避免管道与动力载荷发生共振。

3.3 椭圆度变化

通过riks算法计算出在不同椭圆度下模型的临界压溃压力，并施加相应的外压，使动力载荷需替代的外压在数值上保持一致。不同椭圆度下临界外压和施加外压值如表1所示。在模型短轴(y轴)方向施加圆频率为10 rad/s的正弦载荷和余弦载荷，得到对应的临界动力面载荷曲线。

图9 不同椭圆度下临界动力面载荷幅值

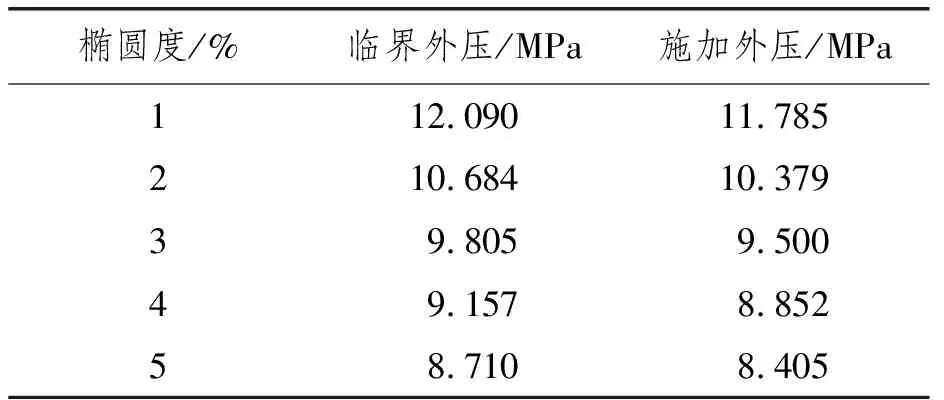
表1 不同椭圆度下临界外压和施加外压

图10 不同外压下临界正弦面载荷幅值组合

从图9可知：在不同椭圆度下正弦载荷和余弦载荷作用下管道的临界压溃面载荷幅值不呈现单调增加或减少的规律，其中椭圆度为1%时的管道临界面载荷幅值相较其他椭圆度存在较大差异。虽然等效的外压在数值上保持一致，但实际上受椭圆度和外压两个变量的同时影响，动力面载荷幅值变化较复杂，在实际工程中须结合工况进行讨论。