连接构件对装配式大型浮体动力响应的影响

(天津大学 建筑工程学院， 天津 300072)

0 引 言

随着海洋空间利用及资源开发的进一步发展，对浮式海上机场、浮式海上可再生能源基地等结构物的需求日益提升。此类结构统称为超大型浮体，具有空间尺度巨大(≥1 000 m)、结构物自身弹性特性(水弹性)明显的特点，在设计、分析和制造方面与传统油气平台有很大区别。近年来，国际上提出了多种超大型浮体的结构形式方案[1]，其中装配式浮体是少数几种可在深远海布置的超大型浮体结构形式。装配式浮体是将数个模块化的浮体通过连接构件连接，形成巨大的整体浮式结构物。与传统箱型超大型浮式结构物相比，装配式大型浮体具有模块化程度高、安装方便、布置灵活、结构简单、建造成本低、经济性良好等优点，值得开展深入研究[2-3]。余澜等[4-5]和丁伟等[6]对三模块的移动式海洋基地(Moblie Offshore Base,MOB)型装配式浮体制作比尺为1∶100的物理模型，进行波浪水池试验；同时建立数值计算模型，分析波浪条件对浮体运动响应的影响。刘超等[7-8]采用刚性模块柔性连接(Rigid Module Flexible Connector, RMFC)模型分析连接构件刚度、浪向角、海况和模块数量对连接构件荷载的影响，得到吃水、重心位置、水深和浪向等因素对浮体运动响应和连接构件荷载的影响。

虽然目前国内已开展一些关于MOB型装配式浮体的研究，但研究方向主要集中于连接构件荷载方向，针对连接方式对浮体相对运动响应的研究较少。模块间相对运动响应是装配式浮体性能的决定性指标，其特性决定装配式浮体的工作性能。本文采用数值方法，基于三维势流原理，采用RMFC模型，研究连接方式对浮体模块间相对运动响应和连接结构荷载的影响，为装配式大型浮体连接构件设计优化提供参考和建议。

1 计算原理

对装配式大型浮体的计算采用RMFC模型，假定连接构件的刚度远小于浮体模块的刚度，模块内部变形远小于模块间的相对位移，即可认为各模块为刚体，连接构件承担所有变形。关于RMFC计算模型，已有研究[9]表明其可有效模拟装配式大型浮体运动响应，浮体运动的频域响应方程为

[-ω2(M+A)+(-iωB+C)]u=Fw+Fc

(1)

式中：M为浮体系统的质量矩阵；A为流体附加质量矩阵；B为附加阻尼因数矩阵；C为附加静水恢复力因数矩阵；u为复数形式的浮体运动响应幅值向量；Fw为波浪激励力。这些参数可用水动力计算软件ANSYS AQWA计算而得。Fc为连接构件作用力，计算式为

Fc=Acu

(2)

式中：Ac为连接刚度矩阵。对于使用弹性连接构件的结构，有

(3)

式中：Kk=diag[k1,k2,…,kn]为表示各连接构件刚度的对角矩阵；AJ为表示各浮体模块间连接点相对位移的矩阵，其维度与连接点个数相关，其内部元素与各连接点相对重心坐标相关。

对于铰接连接的结构，采用增广矩阵[10]的方法，将运动基本方程变为

(4)

此处连接矩阵AJ、连接力Fc的维度由铰接约束的自由度决定，连接矩阵AJ内部元素由铰接位置决定。

2 计算模型及验证

2.1 模型参数

采用的计算模型参照余澜等[4-6]的波浪水池试验，装配式大型浮体由3个半潜式模块组成，单个模块长为275 m、宽为135 m、高为55.75 m，如图1所示。表1列举出浮体模块的主尺寸及相关参数。模块间距为25 m并布置2个线弹性连接单元。此种连接构件可在一定程度上约束其连接部位的相对平动，无法约束连接部位的相对转动，故将其简化为3根与坐标轴平行的线性弹簧。考虑实际结构刚度情况，设定待考察刚度范围为107～1010N/m。

为与波浪水池试验相对应，计算水域深度为300 m，波浪频率范围为0.25～1.00 rad/s。为兼顾艏向与横向波浪作用，选取波浪入射角度为45°。计算海况等级为8级(SS8)，波浪谱采用Bretschneider谱，有效波高为11.5 m，谱峰周期为16.4 s。

图1 装配式浮体示例

结构参数数值上部长/m宽/m高/m275.0125.017.5立柱直径/m横向间距/m纵向间距/m高/m25.090.067.527.5浮箱长/m宽/m高/m270.035.012.5其他参数重心高度(距基线)/m吃水深度/m设计排水量/ktKxx/mKyy/mKzz/m31.0027.75302.0049.8879.8289.94连接构件局部坐标(以模块重心为原点)x/m y/mz/m ±137.5±42.0±24.5

2.2 模型验证

为验证数值方法的可靠性，将数值模型计算结果与余澜等[4-5]和丁伟等[6]的1∶100波浪水池试验结果进行比较。选取波浪入射角度为45°，采用三向连接刚度均为5×108N/m的模块2的六自由度运动响应与试验结果的对比情况，如图2所示。

图2 浮体模块2运动响应幅值算子结果与物理模型比较

从图2可以看出，数值计算结果与物理模型试验数据基本一致，证明数值计算方法的有效性。

3 弹性连接下的响应

装配式浮体不同模块在波浪场中的位置不同，各模块的运动特性(运动幅值、相位)有所差异，模块间会产生六自由度相对位移。由于超大型浮体的功能特性(浮式机场起降飞机、浮式海上基地物资补给等)，模块间的相对位移会对浮体的使用性能产生巨大影响，如过大的相对转动可能使甲板出现起伏或引起连接结构部位破坏等。为了考察连接件对浮体使用性能的影响，计算在8级海况下采用不同连接刚度的弹性连接以及铰接连接的浮体模块六自由度相对运动及连接构件荷载有义值，研究其变化规律。

3.1 弹性连接刚度

为了考察刚度组合对结构物动力响应特性的影响，将同一连接点的3个连接刚度分为两组：无水静力刚度的水平面方向(x，y)以及有水静力刚度的垂直方向(z)。水平面内两刚度Kh设定为相等且与垂向刚度(Kv)独立。两组刚度范围相同，取值为1×107～1×1010N/m，将每个数量级10等分，单个参数共有28个刚度，整体共有784个组合。

3.2 弹性连接模块间相对运动响应

图3 不同连接刚度组合下弹性连接模块间相对运动响应

因为模块1与模块2处于迎浪位置，其相对运动响应大于其他模块间的响应，所以选取模块1和模块2作为考察对象，其相对位移如图3所示。

由图3可得结论如下：

相对纵荡运动受垂向连接刚度影响较小，整体随水平连接刚度增大而减小，当水平连接刚度达1×109N/m时趋于稳定。

相对横荡运动整体随水平连接刚度增大而减小，当水平连接刚度达1×109N/m时趋于稳定，当垂向连接刚度和水平连接刚度均取9×107N/m时，相对横荡运动幅值会异常增大。

相对垂荡运动受水平连接刚度影响较小，整体上随垂向连接刚度增大而减小，当刚度达1×108N/m后基本趋于稳定。

相对横摇运动主要受垂向连接刚度影响，整体上有随垂向连接刚度增大先增大后减小的趋势：当垂向连接刚度达4×107N/m时，达峰值位置；当垂向连接刚度达1×109N/m后，基本趋于稳定。在垂向刚度较低时，相对横摇还受水平连接刚度影响，出现几处异常增大(Kh=Kv=4×107N/m；Kh分别为2×107N/m、6×107N/m、3×108N/m，Kv为2×107N/m)。

相对纵摇受垂向刚度影响较小，整体上随水平连接刚度增大而减小，当水平连接刚度达1×108N/m时趋于稳定。

相对艏摇主要受水平连接刚度影响，随水平连接刚度增大，相对艏摇运动整体上有先增大后减小的趋势，当水平连接刚度达1×109N/m后基本趋于稳定。当水平连接刚度较低时，相对艏摇运动也会受垂向连接刚度影响，出现几处异常增大，异常位置与相对横荡异常点出现的位置相同。

3.3 连接构件荷载

对于装配式大型浮体，连接构件的选取不能只考虑浮体模块的相对运动，还应综合参考连接构件荷载大小。过大的荷载易导致连接构件局部损坏，影响装配式浮体的使用安全。因迎浪位置2#连接构件荷载大于其他位置连接构件荷载，本文选取第3.1节所述刚度组合下该连接构件的荷载进行对比，结果如图4所示。

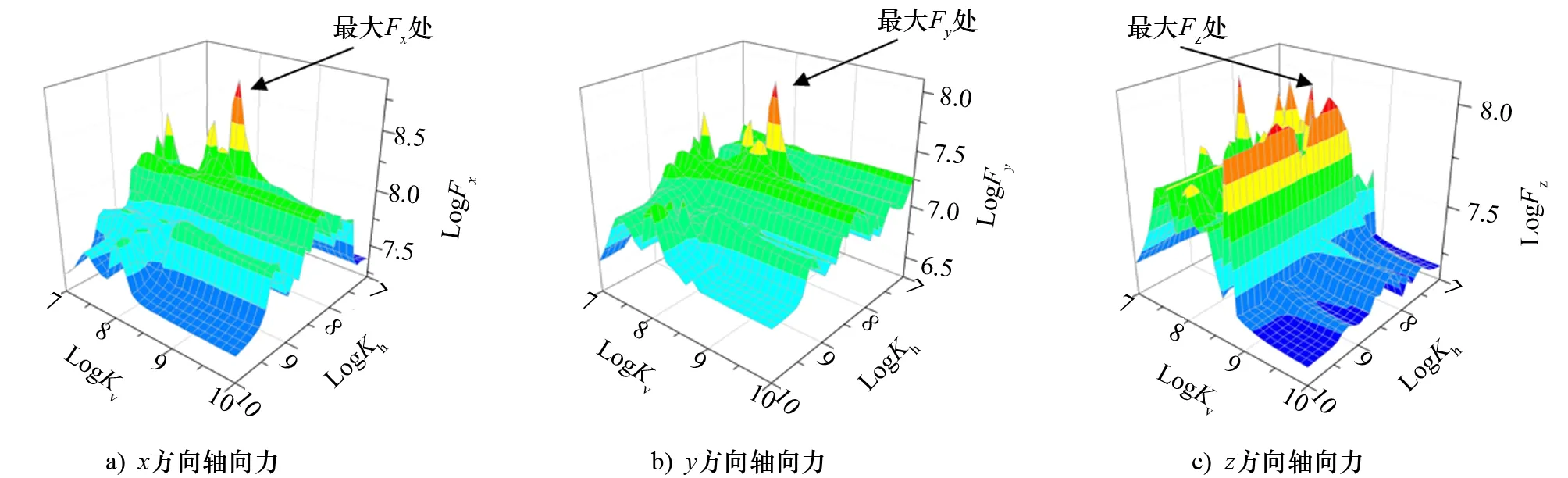
图4 不同连接刚度组合下弹性连接浮体连接构件荷载

x方向轴向荷载和y方向轴向荷载主要受水平连接刚度影响，随着水平连接刚度增大，x方向轴向荷载和y方向轴向荷载呈波动变化，整体上有先增大后减小的趋势，在水平刚度取4×107N/m、8×107N/m、2×108N/m、7×108N/m、2×109N/m时出现峰值。当垂向连接刚度较小(低于1×108N/m)时，垂向连接刚度也会影响y方向轴向荷载。z方向轴向荷载规律较为复杂，当垂向连接刚度较小(低于6×108N/m)时，z方向轴向荷载主要受垂向连接刚度影响；当垂向连接刚度较大时，z方向轴向荷载主要受水平连接刚度影响；当双向连接刚度均较高时，z方向荷载趋于稳定。荷载也出现几处异常增大，且出现位置与相对位移的异常点相同。

3.4 共振频率计算

关于在相对位移和荷载中出现的异常点，猜想是由于连接刚度改变了浮体的自振频率，自振频率与入射波浪频率相近，引起了共振。为此，采用出现异常点位置连接刚度计算几个浮体的自振频率。为了对比说明，也计算几个在正常点连接刚度下的浮体共振频率。结果如表2所示。

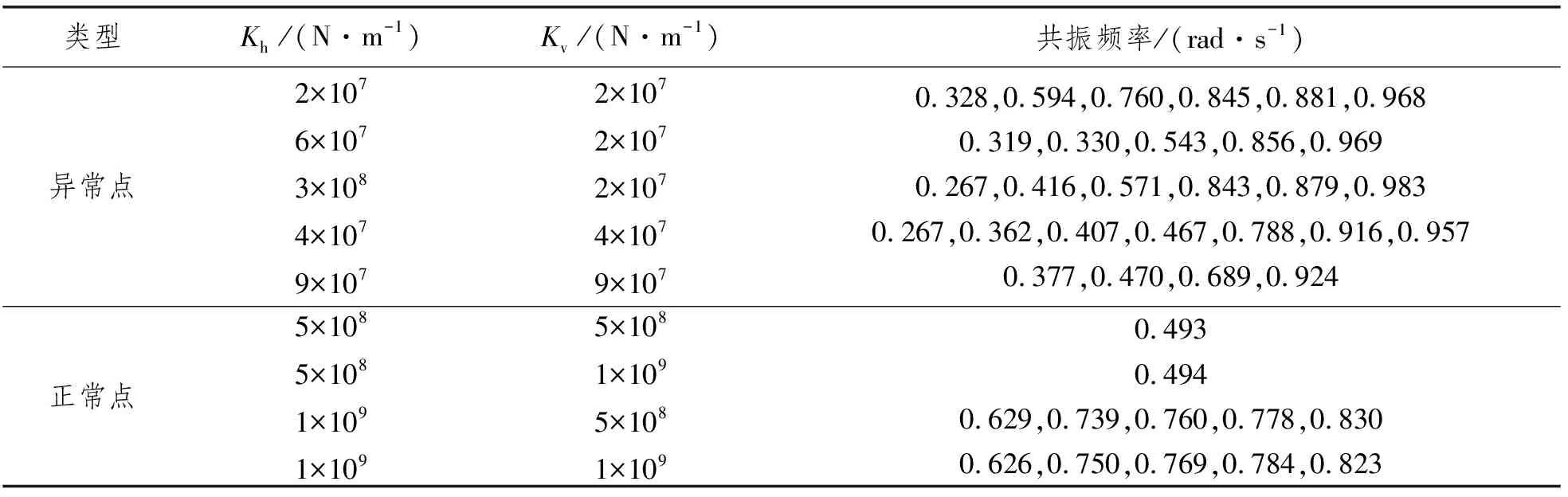
表2 不同连接刚度组合下的共振频率

计算所采用Bretschneider谱谱峰频率为0.38 rad/s，在0.33～0.43 rad/s范围内，聚集了40.6%的波浪能量。正常点的共振频率均不在该范围内，而几处异常点均在这一范围内存在共振频率，从而导致响应值增大，验证了异常点是由共振所引起的猜想。

3.5 铰接连接方式

在实际工程中，由于模块结构、建造工艺、成本等多方面因素，连接构件类型呈多样化趋势，如美国的MOB项目[2]就同时提出了弹性桥型连接方案(Kvaerner Maritime)、铰接方案(Bechtel National.Inc)。采用不同连接形式对装配式浮体运动响应和连接荷载影响开展研究，有重要意义。

参考MOB项目，计算的其他连接形式为铰接形式，具体包括2种连接类型，分别为球型和门轴型，如图5所示。门轴型铰接指相连浮体通过门轴式的铰接构件相连接，不允许发生相对平动，只允许特定方向的相对转动，选取的门轴铰型连接构件只允许相对纵摇方向的位移。球型铰接指相连浮体通过球型铰相连，这种连接方式只约束浮体相对平移，允许浮体相对转动。

图5 门轴型铰接及球铰型铰接示例

计算采用球型铰接与门轴型铰接的装配式浮体模块1与模块2在8级海况下波浪入射角度为45°的相对运动响应以及连接构件荷载，其结果如表3所示。

表3 铰接情况下的计算结果

4 连接方式比选

采用不同连接方式的浮体运动特性有很大差异，且在不同方向上反应数值大小关系并非绝对，为综合评价各类连接结构性能，提出判定标准如下：

(5)

式中：ui为方向i的运动响应有义值；usi为该方向运动响应的参考值；Fi为方向i的连接结构荷载的有义值；Fsi为该方向连接结构荷载的参考值；ai、bi为权重系数，为综合考虑各方面因素，均设定为1，可根据实际需求调整；P为描述连接构件整体性能的无量纲数，P值越小，连接结构整体性能越好。

为确保参考值的可靠性，选取余澜等[4-5]和丁伟等[6]的物模试验对应参数，即在三向刚度均为5×108N/m情况下在8级海况中的响应有义值作为判定连接构件性能的标准值。

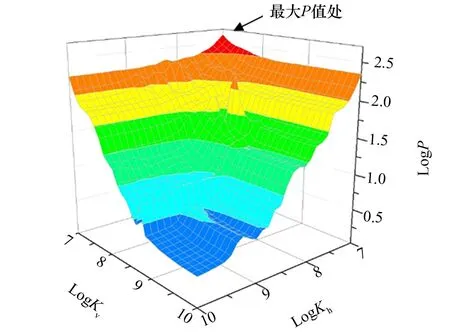
图6 不同连接刚度组合下的P值

各种弹性连接组合的值如图6所示。

从图6可知，在水平方向和垂直方向上，P值均随刚度的增加减小，当水平连接刚度超过6×109N/m，垂向连接刚度超过1×109N/m后，P值基本不变，保持在2.50左右。对于门轴和球铰型连接，P值分别为12.26和48.48，明显劣于在特定连接刚度下的弹性连接。

根据该情况，综合考虑工程实际，可确定对于该种结构布置，推荐的连接类型为弹性连接，连接刚度为水平连接刚度6×109N/m，垂向连接刚度1×109N/m。

5 结 语

采用三维势流理论，根据物理模型试验参数，对采用多种连接方式的三模块装配式大型浮式结构进行建模和动力响应分析，比较运动响应结果，证实数值方法的可靠性。在此基础上，研究在不同刚度的弹性连接以及铰接类型下浮体的相对运动响应和连接构件荷载。

得到如下认识：

(1) 相对纵荡、横荡、纵摇、艏摇位移值主要受水平连接刚度影响，相对垂荡、横摇主要受垂向刚度影响，总体上看，模块间相对位移随刚度增大而减小。连接荷载随连接刚度变化趋势较复杂，总体上看，连接构件荷载随刚度增大先增大后减小，当水平连接刚度超过6×109N/m，垂向连接刚度超过1×109N/m时，连接构件荷载趋于稳定。

(2) 采用弹性连接，在低连接刚度情况下，装配式浮体模块间的相对位移和连接构件荷载对连接模块的刚度变化十分敏感；当弹性连接构件的连接刚度取某些特定值时，由于共振原因，装配式浮体的相对运动和连接构件的荷载响应异常增大，在工程应用中应避免此种现象。

(3) 采用等权重的比较方法，在高刚度下弹性连接的方式优于球型铰接和门轴型铰接的连接方式。对于计算的MOB型装配浮体，推荐的连接类型为弹性连接，连接刚度为水平连接刚度6×109N/m，垂向连接刚度1×109N/m。