基于协整理论的中国医药制造业市场竞争程度与研发资金投入关系研究

尚兴宇，贾辉，陈玉文

依据国际产业标准，医药制造业是十五类国际化产业之一，具有高风险、高投入、高技术、高收益等特点。全球视角下，医药制造业正处于医药技术大规模产业化的初始阶段，预计到2020年进入高速发展阶段，将逐步成为全球经济的主导产业[1]。医药制造业是我国高新技术产业之一，与国计民生有着不可分割的联系，是中国制造2025和战略性新兴产业的重点领域，对推进健康中国的顺利建设有重要的保障作用。尽管我国医药制造业发展起步较晚，但随着市场环境的不断完善、各项扶助政策的助力以及人口老龄化和城镇化等背景，我国医药制造业发展迅猛。据统计，2016年规模以上医药工业增加值同比增长10.60%，增速与2015年同期相比提高了将近1%，是全国工业整体增速4.60%的两倍多，位居中国工业全行业的领先地位。2016年，全国医药工业规模以上企业主营业务收入接近3万亿元，同比增长9.92%，增速较上年同期提高将近1%，增速高于全国工业整体增速5.02%。利润方面，2016年，医药工业规模以上企业实现利润总额3 216.43亿元，同比增长15.57%，增速相比去年同期提高近4%，是全国工业整体增速7.07%的两倍多[2]。

《医药工业发展规划指南》由中国工信部在2016年发布，指南指出了我国医药工业“十三五”期间的总体目标：截止到2020年，医药工业规模效益稳定增长，创新能力显著增强，产品质量全面提高，供应保障体系更加完善，国际化步伐显著加快，医药工业的整体素质大幅提高。其中，行业规模的增长目标要求企业主营业务收入继续保持高速增长，年均增速高于10%，医药工业占工业经济的比重显著增加；技术创新上，研发投入持续增加，全行业规模以上企业研发投入强度达2%以上；竞争程度上，行业重组整合加快，产业集中度不断提高，规模以上企业的前100位整体主营业务收入所占比重提高10%，大型企业对行业未来发展的引领作用进一步加强[3]。

目前来看，我国的医药制造业研发效率水平仍处于较低水平，自主创新能力薄弱的局面仍未打破，由“仿制药大国”向“创新药大国”转变进程缓慢。规模以上企业研发投入强度远低于世界知名跨国医药企业的10%，研发资金投入严重不足，行业集中度较低，小微企业较多及大型企业对行业发展引领作用不足则是造成这一严峻形势的主要原因。

1 文献回顾

1.1 不相关说2007年，吴延兵[4]基于2002年中国工业企业普查数据，对538个四位数制造业的数据对市场结构与研发支出建立单方程回归模型进行实证研究，发现市场集中度与研发强度之间不存在显著相关性。同年，陈仲常和余翔[5]运用《中国科技统计年鉴》中1997—2003年我国大中型工业企业产业层面的面板数据对行业竞争与研发投入关系进行研究，发现行业中的竞争水平在总体上对企业的研发投入没有明显影响。

1.2 负相关说2014年，张航[6]以《中国科技统计年鉴》与《中国统计年鉴》2006—2013年制造业28个行业的分类数据，分别以技术进步和勒纳指数衡量研发投入和市场竞争程度，建立固定效应回归模型，得出在成长型行业竞争程度与研发投入呈负相关关系。2015年，齐东飞[7]以2010—2012年创业板上市公司774个观测值为研究样本，以赫芬达尔指数(HHI)和研发支出为衡量指标，进行回归分析实证考察市场竞争度对不同行业企业研发创新投入的影响，研究发现:在制造业中两者呈显著负相关。2012年，董秀军[8]采用《中国高技术产业统计年鉴》和《中国科技统计年鉴》2002—2009年我国医药制造行业的规模以上工业企业层面和高技术产业层面的面板数据，采用企业数量表示市场集中度，运用多元线性回归等分析方法进行研究，得出行业竞争程度对医药制造企业研发的影响存在负相关性。

1.3 正相关说2010年，谢子远和梁丹阳[9]以2009年《中国火炬统计年鉴》中54个高新区的数据为基础，分别以企业数和研发投入强度为衡量指标，采用加权最小二乘法，研究高新区企业竞争程度与研发投入的关系，得出市场竞争程度与高新区研发投入强度正相关。2012年，柯东昌[10]以我国中小板与创业板上市公司2007—2010年数据为样本，以赫芬达尔指数(HHI)衡量市场竞争程度，研发投入/营业收入衡量研发强度，通过对1 260个观测值的全样本实证分析，得到结论:竞争性越强，垄断性越高，则研发强度越大，即两者呈现正相关的关系。2016年，别春晓等[11]以2005—2013年《中国高技术产业统计年鉴》和《工业企业科技活动年鉴》相关数据为基础，采用因子分析回归法研究医药行业中企业竞争程度等与中国医药子行业研发投入的相关性，得出医药行业中企业竞争程度与三个行业研发投入存在正相关性。

1.4 双向影响说1984年，Scott[12]通过对1974年全美的437个工业企业共计3 388个经营单位的数据进行相关性研究发现，使用四场商集中度作为市场竞争程度衡量指标，市场结构与企业研发活动倒“U”型函数关系成立。2010年，孙晓华与田晓芳[13]基于2006年国家统计局发布的中国工业37个细分行业的统计数据，构建联立方程模型，实证检验了(产业角度)市场力量和技术创新之间的内生性问题，发现市场力量与技术创新存在双向因果关系。

综上所述，国内外学者在市场竞争程度与研发资金投入关系方面的研究，依其研究对象不同，研究的时间结点不同，分别得出了不相关、负相关、正相关、双向影响四种结论。结论差距较大，且研究大多为多因素研究，均未对两个变量在时间序列上的长短期关系及因果关系进行深入研究。2018年1月,笔者采用《中国高技术产业统计年鉴》中1995—2015年我国医药制造业的相关时间序列数据，运用协整检验，格兰杰因果检验及误差修正模型，对我国医药制造业市场竞争程度与研发资金投入之间长、短期关系及格兰杰因果关系进行系统研究，为未来研发资金投入和医药制造业创新能力提升提供参考。

2 研究设计

2.1 指标选取与数据来源本文分别选取企业数(X)和研发经费内部支出(Y)来衡量我国医药制造业的市场竞争程度与研发资金投入。考虑到除市场竞争程度外，其他因素也会对研发资金投入产生影响，所以本文根据数据的可获得性以及借鉴相关文献，引入企业规模作为控制变量，以主营业务收入(Z)衡量，从而尽量确保结果的真实性。本文选取1995—2015年间，中国医药制造业的相关数据，数据均选取自《中国高技术产业统计年鉴》。由于时间序列变量可能存在异方差，因此将变量对数化处理以增强结果的可靠性。对数化后的变量记为LNX，LNY和LNZ。相关原始数据见表1。

2.2 研究方法本文运用Eviews 7.2统计分析软件进行实证研究，主要步骤为：首先对相关变量进行平稳性检验(augmented dickey-fuller，ADF)；其次在数据平稳的基础上进行协整检验，以确定变量之间是否存在长期协整关系，并用普通最小二乘法(OLS)进行回归分析；然后建立误差修正模型(error correction model，ECM)，以描述两者之间的短期动态均衡；最后选取最优滞后阶数并进行格兰杰(Granger)因果检验，确认两者间究竟存在哪种因果关系。

表1 1995—2015年中国医药制造业企业数、研发经费内部支出与主营业务收入相关数据

注：X为企业数，Y为研发经费内部支出，Z为主营业务收入，LNX、LNY、LNZ为各种指标对数化后的变量

3 实证分析

3.1 ADF检验经济时间序列大都是非平稳的，采用时间序列数据建立计量经济学模型，首先必须对用统计数据构造的时间序列进行平稳性检验，有效减少伪回归。同时平稳性检验可以检验出变量是否具有同阶单整性，是否能进行回归分析。运用Eviews7.2软件对对数化的变量LNX，LNY和LNZ分别进行ADF检验，检验结果见表2。由表2可知，原时间序列经过一阶差分后，D(LNX),D(LNY)和D(LNZ)在 10%的显著水平下拒绝原假设，即I(1)序列为平稳序列，3个变量序列为一阶单整序列，具备协整检验条件。

表2 变量的ADF检验结果

注：c,t,k分别表示检验类型中的截距项、时间趋势项、滞后阶数；D(LNX)、D(LNY)、D(LNZ)是LNX、LNY、LNZ的一阶差分序列；a表示变量差分后在1%～10% 的显著性水平下通过ADF平稳性检验

3.2 协整检验协整检验的目的是为了衡量单独的变量之间长期的平稳线性和均衡关系，当两个变量经过平稳性检验，结果为同阶单整后，可以合理推测这两个变量在长期内是平稳的时间序列线性组合并可能存在协整关系，会对该序列继续进行协整分析[14]。EG 两步法和 Johansen检验是协整分析中常用的两种方法，Johansen检验法适用于检测多个变量之间的关系[15]。本文采用Johansen检验为协整检验方法，对变量间长期均衡关系进行协整检验，由表3可知，在5%的显著性水平下，变量迹(Trace)检验和最大特征根 (Maximum Eigenvalue)检验结果表明变量间存在协整关系。

表3 Johansen协整检验结果

分别以LNY和LNX作为被解释变量，用普通最小二乘法建立变量间的长期回归模型，回归结果见表4，表5。

表4 以LNY为被解释变量的回归结果

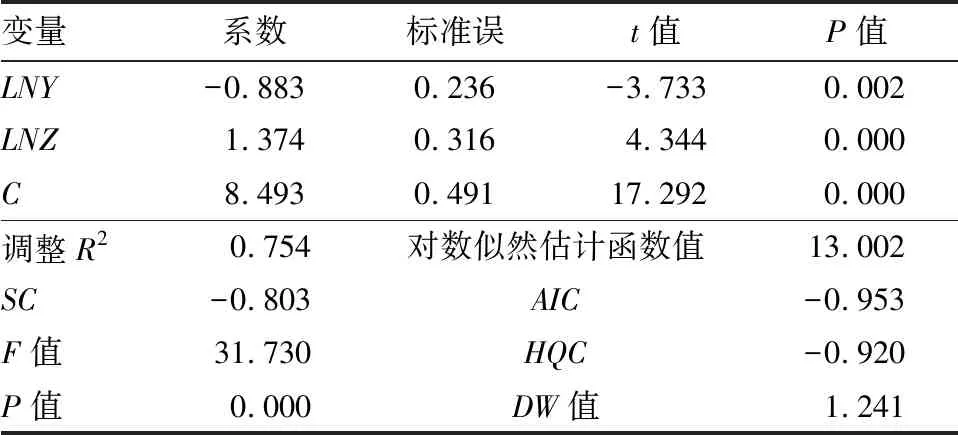
表5 以LNY为被解释变量的回归结果

根据结果得出以下长期回归方程，分别记为方程(1)和(2)：

LNY=-0.494LNX+1.430LNZ+5.223

(1)

LNX=-0.883LNY+1.374LNZ+8.493

(2)

回归结果中，调整R2均接近1，表明方程的解释程度较高，方程拟合度良好。F值也较高，对应的P=0.000，说明整个模型是显著的，两组回归方程是基本有效的。从长期来看，LNX对LNY的弹性为-0.494，LNY对LNX的弹性为-0.883。由于两者的因果关系并未明确，所以做出以下两种假设：假设1：企业数每增加 1%，研发经费内部支出就降低 0.494%；假设 2：研发经费内部支出每增加 1%，企业数就减少 0.883%。

3.3 建立误差修正模型根据格兰杰表述定理，一组具有协整关系的变量一定具有一个误差修正模型(ECM)，用以描述两者之间的短期动态均衡。故利用上述检验结果，可建立我国医药制造业企业数(LNX)与研发经费内部支出(LNY)之间的误差修正模型，模型结果见表6。

表6 误差修正模型结果

模型记为方程(3)：

ΔLNX=-0.441ΔLNY+1.325ΔLNZ-

0.441ECM(-1)-0.103

(3)

式(3)中，误差修正项系数为-0.441<0，符合反向修正机制，表明我国医药制造业研发资金投入数在短期内每变动1个单位，相应的企业数将向反向变动0.441个单位，且变量之间偏离长期均衡状态时，会以0.441的调整速度向长期均衡状态调整。3.4 格兰杰因果关系检验为进一步验证在协整检验中做出的假设，确认两者间究竟存在哪种因果关系，采用Granger 因果检验法对滞后1期到滞后5期LNY和LNX的因果关系进行检验，结果见表 7。结果表明，当滞后阶数为1时，LNY是LNX的Granger原因，LNX不是LNY的Granger原因。LNZ作为控制变量，在此不做结果讨论。不同滞后期下，上述协整检验中假设1，2均成立，即滞后1～3期，在95%的置信度水平下研发经费内部支出是企业数的格兰杰原因，研发经费内部支出每增加1%，企业数减少0.884%。滞后5期，在83.1%的置信度水平下，研发经费内部支出是企业数的格兰杰原因，企业数每减少1%，研发经费内部支出增加0.494%。

4 结果与建议

4.1 结果本文采用 《中国高技术产业统计年鉴》中1995—2015年我国医药制造业的相关时间序列数据，通过协整检验，格兰杰因果检验及误差修正

表7 格兰杰因果检验结果

模型，对中国医药制造业市场竞争程度与研发资金投入之间的长、短期及格兰杰因果关系进行系统研究，得到以下结论：(1)研究期间内，滞后1～3期，研发经费内部支出是企业数的格兰杰原因，即研发资金投入的变动会导致市场竞争程度的变化；滞后5期，企业数是研发经费内部支出的格兰杰原因，即市场竞争程度的变化会导致研发资金投入的变动。说明医药制造业市场竞争程度与研发资金投入存在双向影响关系，药企可以通过研发投入的增加，进而在短期内提高企业核心竞争力；而在较长时间内，企业数的减少会促使企业加大研发资金的投入。(2)研发经费内部支出与企业数间存在协整关系，即长期稳定的均衡关系。滞后1～3期，研发经费内部支出每增加 1%，企业数减少 0.883%。即中国医药制造业市场竞争程度会在研发资金投入的拉动下，呈现长期负向的影响结果。随着研发资金投入的降低，行业中企业数会减少，市场竞争程度会提高；但短期内，研发经费内部支出每增加1%，企业数减少0.441%。与长期稳定的均衡关系相比，短期内研发资金投入并不会使市场竞争程度产生较大改变，但随着时间的推移，短期关系会逐渐向长期均衡关系调整修正，市场竞争程度对研发资金投入的拉动作用将变得显著。说明医药制造业企业长期持续的研发资金投入会逐渐改变市场竞争程度，且随着时间的推移，行业的重组整合加快。(3)滞后5期，研发经费内部支出是企业数的格兰杰原因，企业数每减少1%，研发经费内部支出增加0.494%。即市场竞争程度对研发资金投入有负向拉动作用，随着医药制造业企业数减少，市场竞争程度降低，会大幅降低企业在无效竞争上的投入，增加在创新研究方面的投入。

4.2 建议(1)相关政府部门应加强对我国医药制造企业的有效监管，促使规模以上医药企业实力不断增强，发挥规模以上医药企业对行业的引领作用。在保护市场竞争的同时，鼓励市场适度竞争，加快行业重组整合，进一步促进我国医药制造业的研发资金投入，提高创新能力。(2)我国各医药企业应进一步加大研发资金投入力度，在提高医药企业创新能力的同时促进行业的良性竞争，根据企业竞争力的不同进行优胜劣汰，从而促进我国医药制造业的持续健康发展。

4.3 研究的局限性本研究仅对整个医药制造业市场竞争程度与研发资金投入之间的长、短期关系及格兰杰因果关系进行了系统的研究。为确保研究的可靠性，在后续研究中还应对医药制造业分类进行深化分析，以增强研究的针对性。