电液位置伺服系统的设计与仿真分析
2019-05-24盛夕正钟晓勤纪琦强
盛夕正, 钟晓勤, 徐 轶, 纪琦强
(上海应用技术大学 机械工程学院, 上海 201418)
0 引 言
电液伺服系统是一种由电信号处理装置和液压动力机构组成的反馈控制系统[1],综合了电气和液压双方面的优点,具有控制精度高、响应速度快、输出功率大、信号处理灵活、易于实现各种参量的反馈等优点[2-3]。因此,电液伺服系统在负载力(矩)大、响应速度快的场合最为适合,其应用已遍及工业制造、航空航天、交通运输等工程领域[4-5]。为了使在校学生对电液伺服系统及其应用有更深刻的理解,设计了电液位置伺服系统试验台。
1 电液位置伺服实验系统的组成及工作原理
电液伺服系统一般由控制、执行、反馈、能源等装置组成[6]。控制装置接受输入信号,通过转换后,变成液压参量,对执行机构进行控制、驱动负载按期望轨迹运动。
电液位置伺服实验系统控制原理框图如图1所示,由计算机给定位置指令输入信号ui和反馈输入信号uf进入伺服控制器,信号经过放大转换后使伺服阀的阀芯产生相应方向且与此偏差成正比的开口量,在负载压力一定的情况下,对应于一定流量的液流进入双作用伺服缸,实现对被控制量位移的控制。同时,由位移传感器将活塞杆的位置x以反馈电压uf实时反馈到系统的输入端[7-8]。
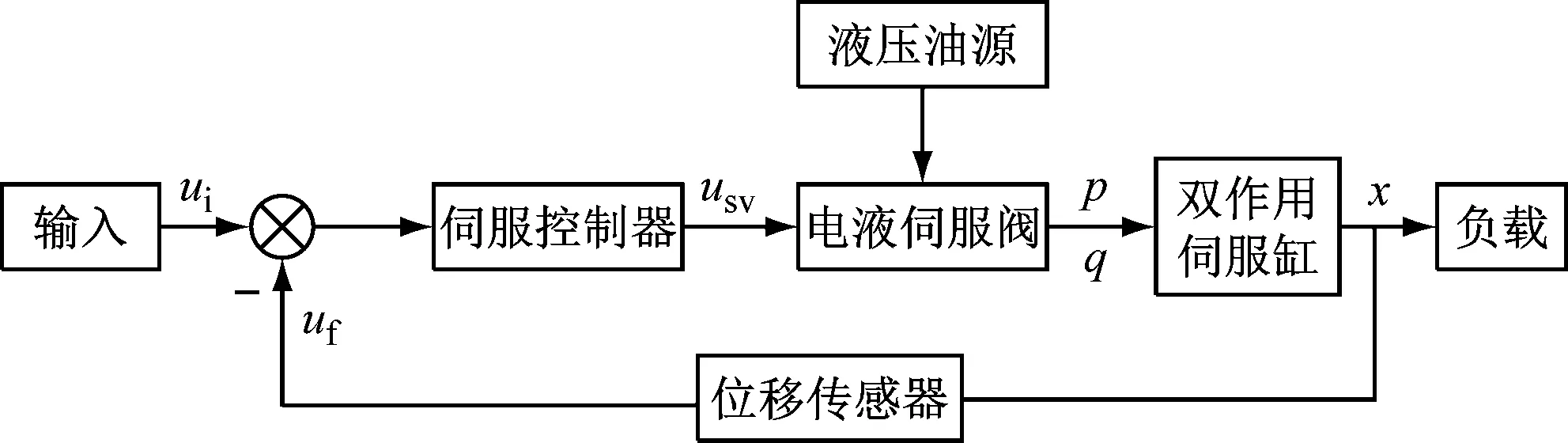
图1 电液位置伺服实验系统原理框图
2 电液位置伺服系统的设计
电液位置伺服系统的液压回路如图2所示。系统使用两套独立能源装置,以减少伺服控制部分与比例加载部分间相互干扰。双作用伺服缸活塞的一端与惯性负载固连,另一端接阻尼器,加载缸将比例加载力通过质量负载作用到伺服缸。

1-电动机; 2-变量柱塞泵; 3-电磁溢流阀; 4-蓄能器; 5-电液伺服阀; 6-压力传感器; 7-阻尼器; 8-双作用伺服缸; 9-质量负载; 10-定量液压泵; 11-比例溢流阀; 12-电磁换向阀; 13-加载缸; 14-风冷却器
图2 电液位置伺服系统工作原理图
伺服控制部分由变量柱塞泵、电磁溢流阀、电液伺服阀、压力传感器、蓄能器、双作用伺服缸及阻尼器等元件组成。系统的工作压力由电磁溢流阀3-1进行调节[9]。电液伺服阀5是系统的核心部件,将输入到伺服控制器的信号放大转换后输入电液伺服阀5的控制线圈。在双作用伺服缸8的两腔各有一个压力传感器6-1和6-2用于实时监测液压缸两腔的压力变化,反映系统工作压力状态。阻尼器7提供阻尼力和缓冲作用。
液压加载部分由定量液压泵、单向阀、比例溢流阀、电磁溢流阀、蓄能器、3位4通电磁换向阀、压力传感器、加载缸等组成。加载部分用于施加载荷,选用定量液压泵驱动。电磁溢流阀3-2为安全阀,加载压力由比例溢流阀11调节。
3 系统元件选型
3.1 负载分析与计算
(1)
经过负载以及活塞的运动计算,得到如图3所示的液压缸端的负载-速度关系,由计算可得系统的最大负载功率Nmax,L=2.6 kW,最大负载功率时的液压缸负载力和速度分别为:Fmax,L=32.557 kN,vmax,L=0.08 m/s,amax,L=1.5 m/s2。
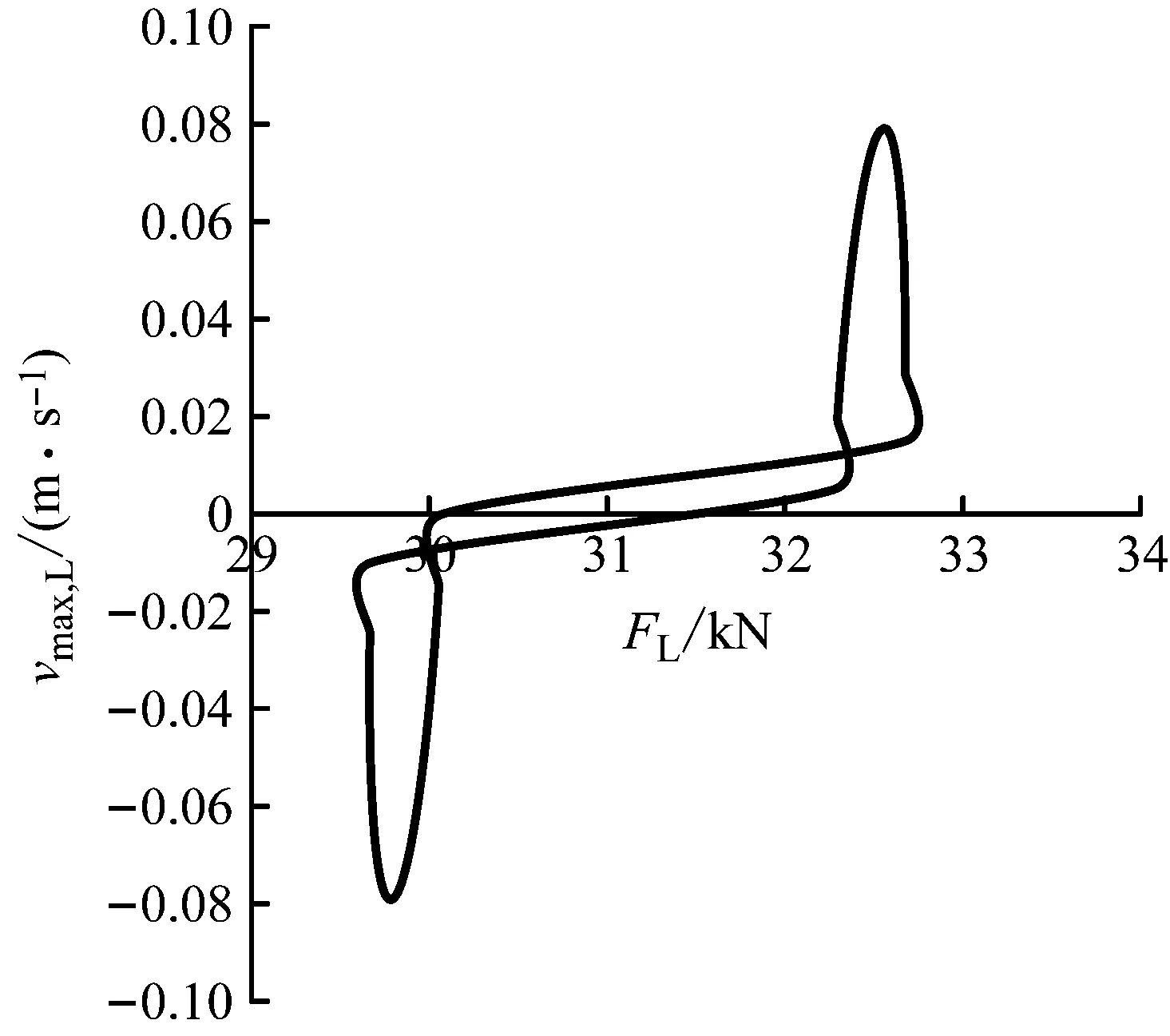
图3 负载-速度关系
3.2 确定供油压力及双作用伺服缸
为了使液压动力元件能与负载做到最佳匹配,初步确定液压缸有效作用面积为:
(2)
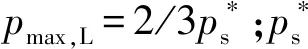
按照液压工程手册进行修正,取活塞杆直径d=63 mm,取液压缸内径D=90 mm,液压缸作用面积Ap1=32.44 cm2,活塞有效行程为0.24 m,确定电液位置伺服系统供油压力ps=15 MPa。
3.3 确定电液伺服阀型号
电液伺服阀流量应满足液压缸活塞杆最大运动速度,故根据最大功率点的速度计算此时的额定负载流量qmax,L,同时为了保证系统的可靠性将数值增大15 %。
qmax,L=115%×Ap1·vLm=17.91 L/min
(3)
最大负载功率时的阀口总压降为:
pv=ps-Fmax,L/Ap1=5 MPa
(4)
为保证系统的响应速度,考虑伺服阀的固有角频率高于液压动力元件的固有角频率3倍以上,根据MOOG D661系列电液伺服阀的响应频率特性曲线,选用型号为D661-3035C G30HOAA4NSM2HA的电液伺服阀。该阀的最高工作压力为35 MPa,流量增益Ksv=1.12 cm2/(s·V),阻尼比ξsv=0.7;阀口压降为5 MPa时的最大流量qom=67 L/min,对应的阀开口量占比为26.7%,响应角频率为ωsv=1 100 rad/s。
磁致伸缩位移传感器型号为CI8P-2A60R03770240 SA4201A,增益为Kf=83.33 V/m。
4 电液位置伺服系统的数学模型及性能分析
4.1 双作用伺服缸传递函数的建立
由于双作用液压缸上的负载为惯性负载、干摩擦负载及加载力,故忽略弹性负载和结构柔度的影响[12-13],双作用伺服缸活塞位移xp(t)对负载流量qL0(t)的传递函数为:
(5)
式中:ωh为动力元件的液压固有角频率,经计算ωh=346.1 rad/s;ξh为动力元件的阻尼比,取ξh=0.2。
液压缸活塞位移xp(t)对负载力FL(t)的传递函数为:
(6)
式中:Kce为动力元件总量-压力系数,经计算Kce=2.10×10-12m3/(s·Pa);βe为油液的等效体积弹性模量,取βe=7×108;Vt为液压缸的总容积,经计算Vt=820 cm3。
4.2 电液伺服阀传递函数的建立
由于电液伺服阀的响应角频率大于3倍液压动力元件的固有角频率,即ωsv>3ωh,电液伺服阀的传递函数可以看成是惯性环节,其传递函数为:
(7)
4.3 电液位置伺服系统传递函数
电液位置伺服系统的传递函数方块图如图4所示。
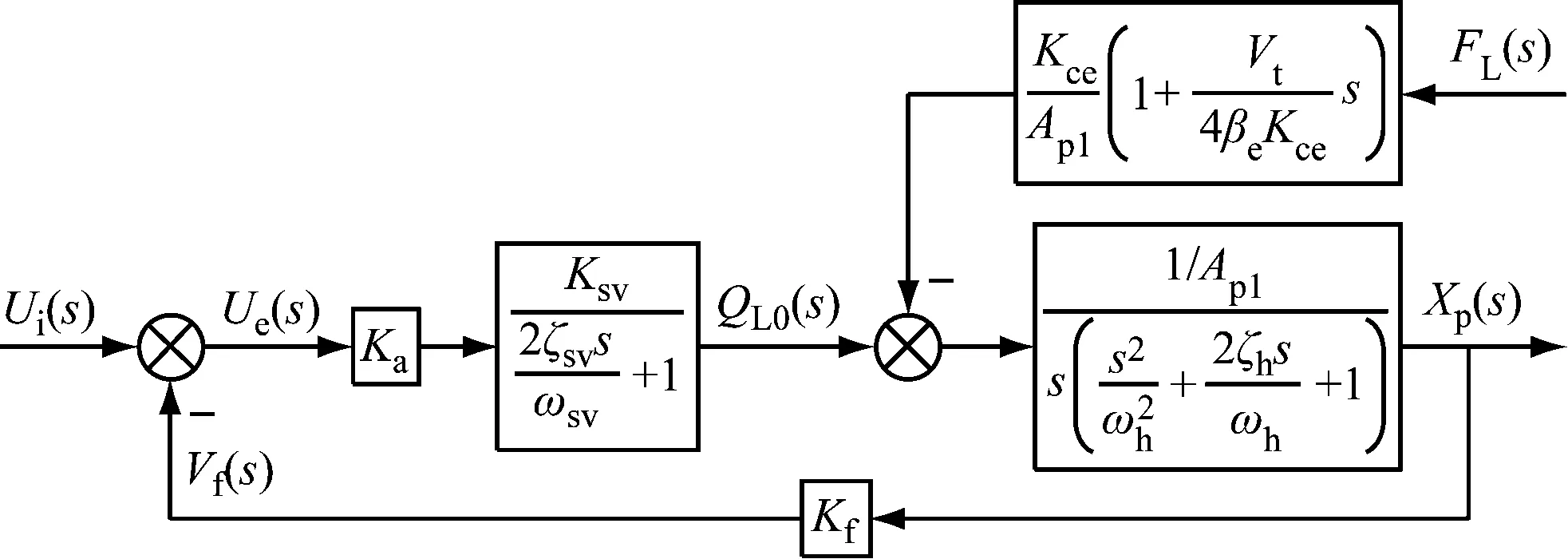
图4 系统传递函数方块图
电液位置伺服系统的传递函数为:
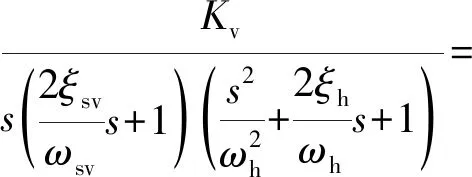
(8)
式中:Kv为系统的开环放大系数,Kv=KfKaKsv/Ap1,经计算伺服放大系数Ka<48.1,按照系统的精度要求,经仿真试验取Ka=30。
4.4 电液位置伺服系统仿真及性能分析
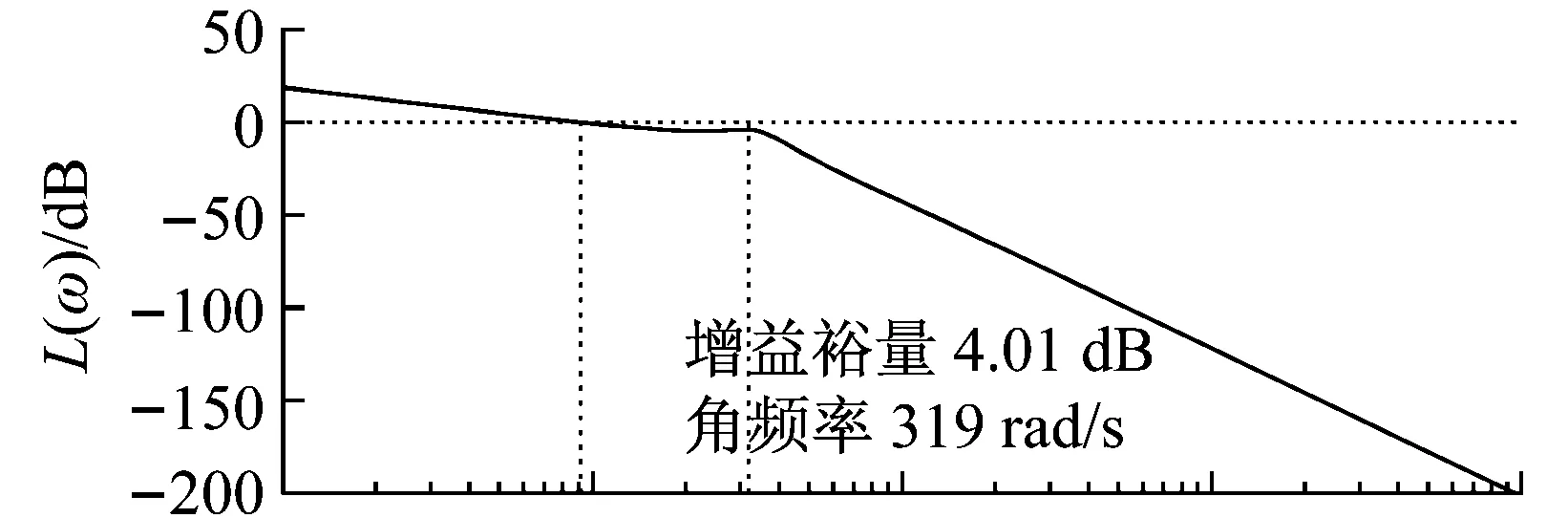
利用Matlab软件建立系统仿真计算程序并运行,对系统做线性分析[14],得到仿真结果如图5所示。系统在穿越角频率ωc=91.7 rad/s,相位裕量Pm=76.8°,在角频率ωc=319 rad/s处增益裕量Gm=4.01 dB。相位裕量和增益裕量均在较为合理的范围内,能够保证系统的稳定性,满足系统稳定性要求。

为了对系统输出性能进行预估,利用Matlab/Simulink仿真软件对系统进行仿真[15]。建立如图6所示仿真模型,输入1 mm位移的阶跃信号指令,运行仿真模型。仿真结果如图7所示,系统最大超调量为6.75 %,位移上升95 %时间约为30 ms,峰值时间为37 ms,在55 ms后系统达到稳定状态(响应曲线衰减到与稳态值之差不超过稳态值的±5 %)。输入相关正弦信号得出系统的输入、输出曲线,如图8所示。仿真结果的系统最大误差为54 μm,满足系统控制精度的要求,系统的输出能够稳定跟随输入信号的变化[16]。电液位置伺服系统实验台如图9所示。
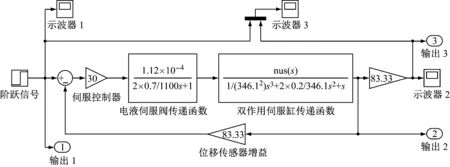
图6 电液位置伺服系统的Simulink模型
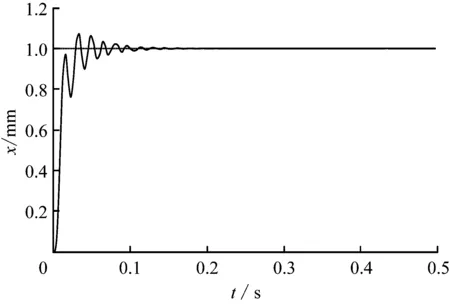
图7 阶跃响应图
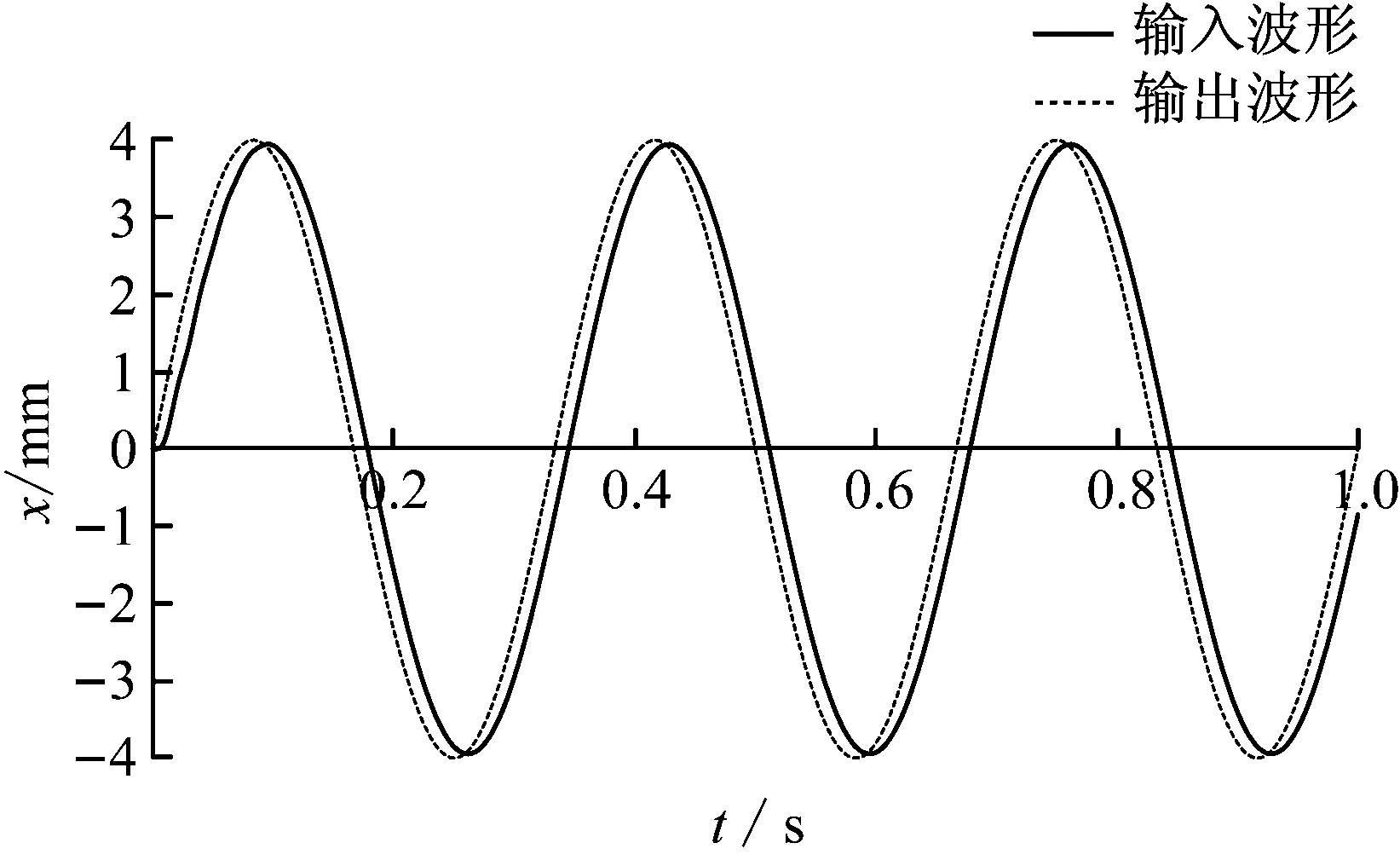
图8 系统输入输出波形图

图9 电液位置伺服系统实验台
5 结 语
本设计建立了基于电液伺服控制技术的试验平台,实现了对输出量的位置控制,伺服控制系统组成合理完整,并应用Matlab/Simulink软件对系统进行仿真分析,仿真结果表明,系统满足位置控制的精度要求,达到设计目标。该电液伺服系统的实验平台已成功应用于教学科研研究,解决了电液伺服控制技术在生产、应用实施过程中产生的关于实验研究及训练的真空区域问题,有较好的实用价值。
