一类流水线车间调度模型及其算法研究

张元康 齐雪

(安徽科技学院信息与网络工程学院， 安徽 凤阳 233100)

1 问题重述

程远方等人曾研究过一种最基本的流水线车间调度问题[1]。我们将在此基础上进一步探讨置换流水线车间调度问题。问题描述如下：某车间生产汽车用金属管件，车间有3台机器，分别用于完成弯折金属管、焊接连接处、装配各单元3道工序；加工6种加工件，加工件分类为1#、2#、3#、4#、5#、6#；每种加工件都需要经过3道工序，首先进行弯折，然后进行焊接，最后进行装配；在进入工序之后，每项加工工序都不允许打断，但前后两道工序之间可以等待一段时间；每台机器每次只能处理1个加工件。各工序下每种加工件所需耗时如表1所示。

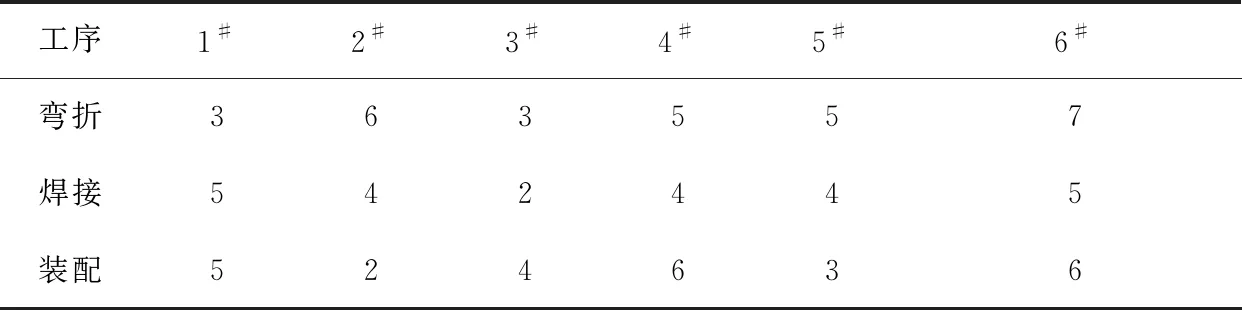
表1 各工序下每种加工件所需耗时 min

假定，在等待进入下一台机器处理的过程中，不允许排在后面的加工件“插队”。通常，总加工时间越短，成本越低，因此，需要设计合理的加工顺序使总加工时间最短。

2 模型的假设、符号说明与问题分析

2.1 假设

(1) 每个加工件按特定的加工顺序进行加工，即弯折→焊接→装配。

(2) 进入工序之后，每项工序不允许打断，但紧邻的工序之间可以等待。

(3) 每台机器每次只能处理1个加工件，特定机器处理特定的工序。

(4) 等待下一台机器处理时，不允许排在后面的加工件插队。

(5) 所有机器同时运转，工件在机器之间的转移时间不计，即机器的准备时间不计。

(6) 所有机器正常运行，不会出现故障。

(7) 所有工件同时到达，到达时间设为0。

2.2 符号说明

模型中各符号代表的含义如下：n表示工件数；m表示机器数；T表示3×6的加工时间矩阵；tij表示第j个工件在第i台机器上的加工时间；cti表示第i个工件的完工时间；ctmax表示最长完工时间，ctmax=maxi=1，2，…，n(cti)；Fmax表示最长流程。

2.3 问题分析

求最短完工时间，陈蓉秋曾研究了这个问题的解法[2]。假设所有工件同时到达，且到达时间为0。最长完工时间最短，则ctmax达到最小。即，最后加工工件的停留时间及最长流程最短。在车间调度的专业术语中，最长完工时间为Makespan指标。建立以最长完工时间为函数值、工件加工顺序为自变量的模型，再根据适当的算法求出加工顺序，两者结合可以得到最优顺序，最后求解得到最短的完工时间。

针对多阶段排序问题，可以建立快速求解的贪婪算法，但该算法仅在解决计算量小的问题时操作才比较简单。我们必须寻求一种可信度较高，且能够简单求解较复杂问题的算法。在解决流水作业排序问题时，可应用启发式算法、遗传算法、模拟退火算法和粒子群优化算法，各算法单独或融合应用。遗传算法、模拟退火算法和禁忌搜索算法效果较好，迭代计算量较大，且需算法操作、参数结构选取得当。神经网络算法是一种效果良好的调度求解法，但是应用中需对网络参数和能量函数进行精心设计。启发式算法因其计算量较小的优点，更适用于比较简单的流水线调度问题。当求解要求较高时，可采用遗传算法。

3 算法及ctmax计算

3.1 Johnson算法

根据张鹏等人的Johnson算法研究可知[4]，Johnson算法主要用于n/2/P/ctmax这种情况，为m台机器的启发式算法提供了理论基础。当m为2、3时，流水作业排列与排序问题具有相同的最优解，所以这里是P或F是一样的，与原问题保持一致，所以用P表示。

若T表示2×n的加工时间矩阵，Johnson最优调度法则为：如果min{t1i,t2j}≤min{t1j,t2i}，则工件i排在工件j之前加工。按Johnson法则，则时间复杂度为O(2n)。对Johnson算法作如下改进：

Step1：U1={i/t1i≤t2i}，U2={i/t1i>t2i}

Step2：对U1中的工件按t1i非减顺序调度得到A

Step3：对U2中的工件按t2i非增顺序调度得到B

Step4：将A放在B之前，得到最优加工顺序

3.2 启发式算法

Johnson算法的优点是，操作简单，计算量小。但是，对于m>3的情况，无法用Johnson算法来解决，且Johnson算法只能作为解决问题的一个充分条件。在实际生产当中，大量的多机器生产问题亟待解决，因此人们开始研究启发式算法。应用启发式算法可得到多机器生产的近似最优解，而计算量较小，非常实用。

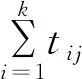
(2) Palmer启发式算法。1965年，Palmer提出了基于工件的加工时间按斜度顺序指标排列工件的启发式算法。聂艳芳曾在VRP的数学模型及其算法中应用了这种算法[6]。该算法的基本思想是，给每个工件赋优先权数，按机器的顺序，机器加工时间趋于增加的工件得到较大的优先数。工件的斜度指标λj为：

(1)

按照斜度不增的顺序排列作业顺序，可以得到1个较优解。另外，Gupta提出了另一种类似于Palmer方法的启发式算法，基于3台机器的Johnson规则最优性，定义工件j的斜度指标λj，然后以与Palmer相同的原则排列工件顺序。

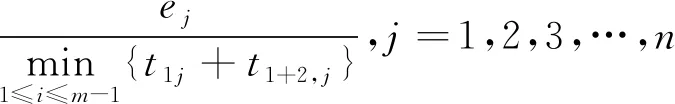
(2)

其中

3.3 ctmax的计算

基于以上算法，得到最优排序的完工时间。假设当前加工顺序为O={o1，o2，…，on}，oi表示排在第i位的工件代号。对于o1，在机器k上的完工时间为其在机器k之前的累计工序时间；对于oi，在机器k上的完工时间取决于前一个工件在机器k上的完工时间，以及oi在前一台机器上的最大完工时间。ci，oj表示工件oj在机器i上的完工时间。于是有(3)(4)(5)递推公式：

c1,o2=t1,o2,ck,o2=ck-1,o2+tk,o1,k=2,…,m

(3)

c1,o1=c1,o1-i+t1,o1，i=2，…，n

(4)

(5)

s1,o1=c1,oi-1=s1,oi-1+t1,oi-1,i=2，…，n

(7)

sk,o1=max(ck,oi-1,ck-1,o1)

(8)

=max(sk,oi-1+tk,oi-1,sk-1,o1)

i=2，…，n，k=2，…，m

根据以上公式，可以排列出最优排序，并通过算法编程计算出最短时间。

4 启发式算法的实现及分析

4.1 CDS算法计算

首先完成CDS算法编程，输入加工时间矩阵，T=[3 6 3 5 5 7；5 4 2 4 4 5；5 24 6 3 6]；接着，调用Matlab程序，由[makespan,sort]=CDS(T)得到计算结果：

makespan= 35

sort=[1 3 4 6 5 2]

sort=[3 1 4 6 5 2]

其中，makespan返回值就是makespan指标的值，sort返回值是近似最优排序。此时这2个sort返回值均为最优解，其makespan指标都为35 min。

为了绘制甘特图，我们对程序稍作改进，得到每个工件在每道工序上的起止时间。为了方便起见，在此只给出程序结果。两种最优解的加工时间如表2、表3所示。表中数据含义，以第二行第4列的(11,15)为例，表示第3个工件从第11 min开始进入第二道第15 min 加工完成。

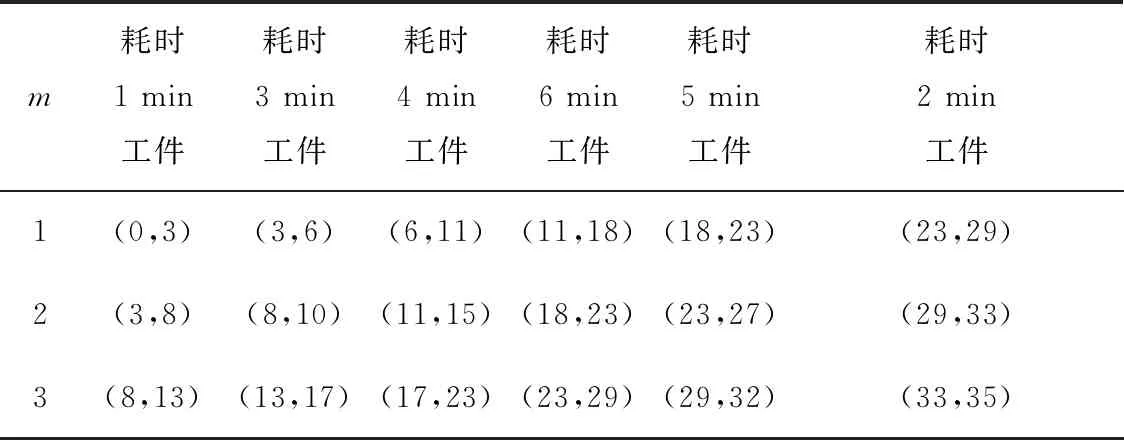
表2 最优解sort=[1 3 4 6 5 2]下的加工时间安排 min

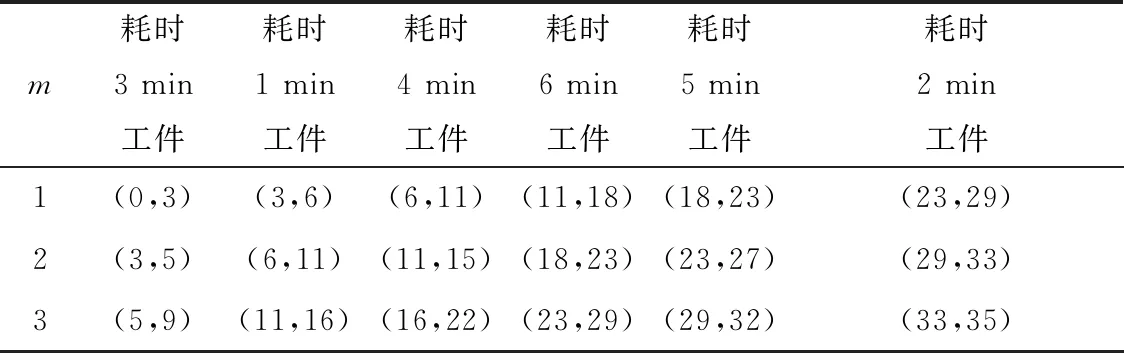
表3 最优解sort=[3 1 4 6 5 2] 下的加工时间安排 min

4.2 Palmer算法和Gupta算法

调用Palmer算法的程序palmer.m，得到如下结果：

λ=[4 -8 2 2 -4 -2]

sort = [1 3 4 6 5 2]

由此得到了与CDS同样的最优顺序，最长完工时间同样为35 min。同时，工件3和工件4的斜度指标均为2。设想一下，如果将这两个任务颠倒，也许结果更优。

然后，将sort = [1 4 3 6 5 2]代入程序Fmax=zxct(T,s)，得到最长完工时间为35 min，从而得到新的最优解。

根据上述Gupta算法的不同斜度指标，编写程序gupta.m，得到最优排序为

sort =[3 1 4 6 5 2]

此最优解与应用CDS算法得到的顺序相同，其中λ=[1.250 0E-001 -1.666 7E-001 2.000 0E-001 1.111 1E-001 -1.428 6E-001 -9.090 9E-002 ]，最长完工时间也为35 min，并且所有的λ都不一样。

4.3 关键工件法

运行程序keygj.m，得到结果：

sort =[1 3 4 6 5 2]

与应用CDS算法所得到的sort 相同，所有其他元素和加工时间矩阵等也都相同。

4.4 讨论分析

根据以上几种启发式算法，得到3个近似最优解(见表4)。

表4 3个近似最优解

在表中，每个sort 出现的次数均不相同，这与算法的设计有关。如排序为小于等于，等于号也可以放在大于之列，而变成大于等于；如排序相等，也可以调换顺序得到不同的调度结果。也就是说，只要对上述算法程序稍加改变，就可以求出达到最优的另一个解。

应用启发式算法，可以一次求出1个全局最优解。由于存在N-P问题，它的全局最优性无法保证，往往只能得到1个近似最优解。选择不同的启发式算法，通过更多的实践检验，才能发现其优缺点。我们可以加大m和n的值，从而进一步了解这些算法的优缺点。

通过对相关文献的梳理，发现关于知识优势的研究主要集中在微观层面(如企业)，而中观层面的研究(如知识链、企业联盟)刚刚起步，至于宏观层面(如国家知识优势)更鲜有研究。鉴于此，本文拟通过引入VRIO模型，从价值性、稀缺性、难以模仿性和组织四个维度探讨知识链知识优势的来源，并分析这四者对知识优势形成的不同作用，以期为知识链知识优势的评价和测量提供一个基本框架。

这里给出一个结论：CDS 算法和关键工件法的解为较优解，Palmer 算法与Gupta 算法适用于只需求解1个快速近似解的问题，当要求较高时可以采用CDS 算法和关键工件法。当然，解决这类问题时除了采用启发式算法，还可以采用其他算法，如遗传算法等。

当m=3,n=6时，这是一个比较简单的问题，可用计算机枚举法求出所有达到最优的加工顺序。根据龚纯等人研究的Matlab最优化算法[7]，运行Matlab程序meiju.m，得到表5所示结果。

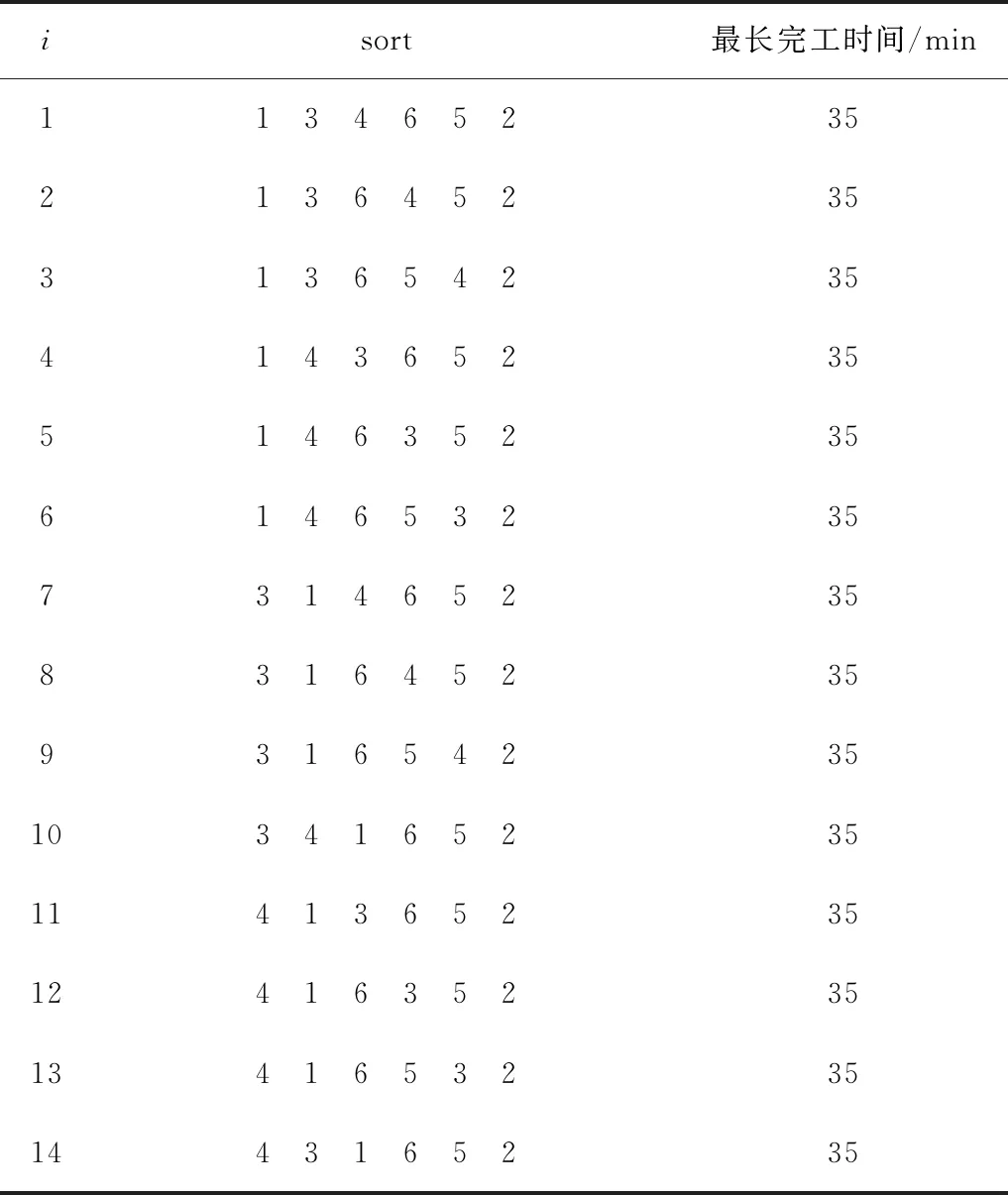
表5 meiju.m程序运行结果

最后,对比启发式算法与枚举法在此问题上的运算时间(见表6)。

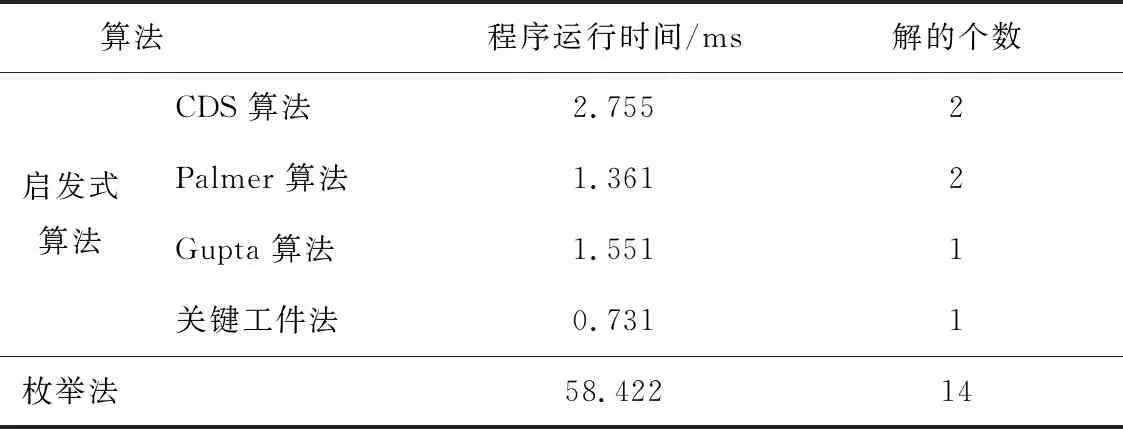
表6 启发式算法与枚举法的运算时间比较

枚举法比启发式算法的运行时间会长很多，但是就所求解的质量而言，枚举法所得解为最优。为了与遗传算法进行对比，我们列出了这些算法的运算时间，也可以通过理论方法计算这些算法的时间复杂度。

5 遗传算法

5.1 遗传算法设计

遗传算法(GA)是Holland于1975年受生物进化论的启发而提出。遗传算法是一种基于自然选择原理和自然遗传机制的搜索算法，其自组织、自适应、自学习和群体进化等能力较强，适用于求解大规模复杂优化问题。运用该算法，可将问题的求解表示成“染色体”适者生存的过程。遗传算法的实现流程包括编码/解码部分和遗传操作部分。其中，遗传操作部分又包括选择、复制、交叉和变异等步骤。受车间调度及其遗传算法的启发[8]，我们运用遗传算法完成以下求解过程。

设定种群大小为M，分别取50、60、80。因为解的结果不唯一，所以用不同的M运行多次，得到全部的全局最优解。迭代代数为N，取1 000。为了使得群体充分进化，设交叉率为1，变异率P为0.1，变异发生的可能性比较小。初始种群随机生成。算法流程分解如下：

(1) 编码与解码。用数字1 — 6分别代表6个任务。

(2) 交叉。在此采用以下交叉方式：

Step 2：从前到后选择父代个体f1中属于S1的基因，以及父代个体f2中属于S2的基因，构成子代个体。

Step 3：类似Step 2，得到子代个体B2,从而得到子代B。

(3) 变异。 按照给定的变异率，对选定的变异个体，随机选择3个整数，1≤u1

(4) 选择。在[f：B：C]中选择适应度最大的M个体作为下一代的父代，可以保证父代的优良基因被保存下来。

(5) 适应度函数。因为目标函数是使得ctmax达到最大，因此，选择上限值为79-ctmax。建立适应度函数，FITNESS=79-ctmax，将使得目标函数最小的M个体作为下一代。

遗传算法步骤如下：随机产生初始种群f；随机两两交叉染色体产生子代B；根据变异概率在子代B中随机选择变异个体，进行变异得到子代C；计算父代与子代的适应度函数，选择最大的前M个体作为下一代父代。为方便起见，直接计算个体在目标函数中的值，选择最小的前M个体作为下一个父代。

5.2 遗传算法计算机模拟结果

对不同取值的M进行迭代，并且针对每个M值运行程序[f,mm,OPT]= ycsf(T,P)，得到表7所示结果。

表7 程序运行结果

种群个体越大，运行时间也越长。我们也可以使得N增大而M不变。但计算机模拟结果表明，当N=10 000，M=50时，可以得到解的个数为12，而运行时间已经达到了72 s。这显然没有使M变化后的计算复杂度变小，且其解也不是最优。

遗传算法中，选用的参数及结构一定要适宜，不同的结构会导致不同的结果。

6 结 语

启发式算法是一种构造方法，3台机器以上即形成N-P问题。目前尚没有出现解决多项式复杂性全局问题的最优化算法，而采用启发式算法可以快速得到次优解。若我们需要快速得到近似解时，Palmer 算法和Gupta 是很好的选择。若需要得到更好的解时，CDS算法和关键工件法是很好的选择。启发式算法以其特别方便，操作简单赢得人们的关注。启发式算法中，还有几种较优算法，限于篇幅未能逐一介绍。如NEH 算法以及在其基础上改进的Rajendran算法，都是优秀算法。遗传算法给出了全部的最优解，并且GA 解的质量往往比启发式算法更好。对于较复杂的车间调度问题，用GA 算法是一个好的选择。车间调度问题限制较多，目标函数也极为明确，所得目标函数相对固定。采用启发式算法找到最优解，且通过枚举给出了所有的解，使该车间调度问题得以完美解决。

本模型及其算法的不足之处是，一般的启发式算法是一种构造性方法，只能给出充分条件。同时，在大数据问题上启发式算法只能给出近似解，而不能达到全局最优解，若对解的要求不高，也可以采用。运用遗传算法虽然可以得到较优的解，但是算法操作和参数结构设定应合适，且需要大量的迭代运算，时间复杂度和空间复杂度都相当高。