基于等价压缩快速聚类的Web表格知识抽取

吴小龙， 曹存根

(1. 中国科学院 计算技术研究所 智能信息处理重点实验室，北京 100190；2. 中国科学院大学，北京 100049)

0 引言

Web表格知识抽取是一种重要的获取高质量知识的途径，在知识获取、知识图谱、网页挖掘、信息检索、问答系统等方面都有广泛的研究意义与应用价值。

Web表格作为一种简洁有效的知识表现形式，富含结构化和半结构化的知识，并且大量存在于网页之中。Google的一项研究表明，大概有1.5亿高质量的关系表存在于万维网之中[1]。Web表格资源丰富，具有结构化和半结构的特点，使得Web表格成为重要的知识抽取来源，并被广泛应用于大规模知识库的构建之中[2]。大型知识库DBpedia和YAGO以维基百科的Infobox表、维基表格 Wikitable 作为主要知识来源之一，Google的知识图谱也将Web表格作为知识融合的主要对象[3]。

传统的Web表格知识抽取方法主要依赖于良好的表格结构和足够的先验知识，但在复杂的表格结构及先验知识不足等情形下难以奏效。针对这类方法的问题，充分利用表格自身的结构特点，以无监督的聚类方法挖掘表格结构共性，从而推测语义结构共性来获取知识，是一条解决问题的新思路。

然而，据作者所知，在目前的文献中尚未发现专门用于Web表格聚类的相关算法，传统的经典聚类方法如密度峰值聚类方法[4](clustering by fast search and find of density peaks，DPC)直接用于表格聚类又将面临相似性度量困难、时间复杂度较高、聚类中心较难选取等问题。

因此，本文提出了一套可面向大规模数据的基于等价压缩快速聚类的Web表格知识抽取方法，通过发掘表格的形式结构类型与特点，并从相似形式结构的表格中推测表格的语义结构，以“同类结构相同抽取方法”的办法从中抽取知识。具体地，本文的主要工作和贡献如下：

(1) 针对重复的DOM(document object model)子树结构造成的表格相似性度量困难问题，本文基于表格形式上的伸缩与语义结构无关的假设，提出了基于DTW(dynamic time warping)的方法来构造两棵DOM树的相似性度量，使得表格相似性度量更符合表格的形式特点。

(2) 通过构造等价距离，将绝大部分的复杂的两个Web表格之间的距离计算等价为构造的基准坐标空间下的欧氏距离计算，缩短单个点对的距离计算时间，并提出了一种自压缩Canopy算法进行预聚类，剔除等价表格，并减少大量不必要的距离计算，以降低聚类时间复杂度。

(3) 为避免半自动选择聚类中心带来的主观性和不确定性，提出了一种确定聚类中心点的启发式算法，解决了聚类中心难以选取的问题。

(4) 结合上述工作提出了一种可面向大规模数据的基于等价压缩的Web表格快速聚类算法，并针对聚类结果构造模板化的抽取算法来抽取知识，所抽取的知识三元组的准确率也达到了令人满意的结果。

1 相关工作

本节将介绍传统的Web表格知识抽取方法以及候选的可用于Web表格聚类的相关算法。

1.1 Web表格知识抽取方法

传统的Web表格知识抽取研究主要通过先验知识库的本体映射、实体对齐，或以大量的人工标记数据作为有监督学习手段，在默认的良好的表格结构下，发掘表格内的实体、概念及其关系，从而抽取知识。

用已存在于知识库中的实体、概念去识别表格的元素，该过程可称之为表格注释[5-6]。基于人之所以能理解表格是因为人脑中拥有对知识的认识，Wang等[7]通过使用知识库Probase的通用概率分类体系(本体)，构造了一种基于表头识别和实体识别的框架，以用于从网页表格中获取新知识。类似地，Ritze等[8]也运用了大型知识库DBpedia，将表格的行和列的内容映射到DBpedia知识库中，以寻找相对应的实体和关系模式，从而推测剩余表格的新实体和关系。另外，Hogan等[9]运用已有的开放链路数据去识别维基百科表格中已有的实体关系，并推测表中其他未被链接的实体和已被链接的实体具有相同的关系，从而获取新的实体关系。Nagy等[10]通过挑选空白、单元格字符数等7个单元格特征，提供了一个可训练的关键单元格定位算法来学习表格的关键单元格的特征。Pinto等[11]将文本文档中ASCII表的每一行标记为非知识行、表头行、数据行、注脚行等，结合空白特征、文本特征、分隔符特征等，构建并训练条件随机场模型，用于表格定位、单元格类型判断等，进而推测表格的知识分布，用以表格抽取。

此外，在良好的表格结构下，可以根据表格内各单元格内容自身的特点及其与附近单元格内容的关系来分析表格内的语义关系。Chen等[12]利用表格的单元格、行和列元素之间的字符串、命名实体以及数字类型的相似性来识别表格的内容模式。Dalvi等[13]通过聚类同类项并结合Hearst模式获得的概念来给这些同类项分配相对应的概念从而获取新的概念实例对。Pivk等[14]将Web表格转化为一个逻辑表格，描述表格元素之间的关系，达到区分表格中的属性单元格和实例单元格的目的。

综上所述，传统的Web表格知识抽取方法主要依赖于良好的表格结构和足够的先验知识，也未能充分利用表格自身的形式结构特点，难以应对复杂的表格结构以及先验知识不足等问题。

1.2 Web表格聚类方法

Web表格由Lautert等[15]根据经验分为如图1所示的类型。一般而言，相似形式结构的表格拥有相似的语义结构。Web表格聚类避免了大量数据标注的资源依赖性问题以及复杂的特征工程问题，通过无监督聚类，发掘表格形式结构的共性，从而发现表格的语义结构，便于将表格分类处理。

图1 Web表格分类图

对于海量的、形式多样的Web表格，具备解决大规模数据问题、发现任意形状簇等关键能力的聚类算法尤为必要。在目前的文献中我们尚未发现专门用于Web表格聚类的相关算法，然而在候选的可用的相关算法中，密度峰值聚类DPC是常见的、较为有效的大规模数据聚类方法。在该方法中，聚类中心是那些相对于它们的邻居有着高密度且它们之间的相对距离较大的点[16]，由两个变量来刻画： 每一个样本点的局部密度ρi，以及它与最近邻高密度点之间的相对距离δi。

局部密度的定义如式(1)所示。

相对距离δi定义如式(2)所示。

总体说来，DPC算法思想简单直观，能够快速有效地发现任意形状的簇，但是其时间复杂度为Ο(N2)，且聚类中心需要人工判断选择。因此，有效降低时间复杂度，实现DPC算法全自动化，对于解决大规模数据聚类、发挥DPC简洁有效的优势有着重要的现实意义。

2 基于等价压缩快速聚类的Web表格知识抽取

本节中，我们从改善Web表格相似性度量、降低时间复杂度以及自动聚类中心选取三个方面提出了基于等价压缩的Web表格聚类算法，以进行表格聚类，然后对聚在同一类的具有相似结构的表格分别使用相同的模板化的抽取方法抽取知识。

2.1 基于等价压缩的Web表格聚类

针对多数聚类算法如密度峰值聚类方法DPC的相似性度量困难、时间复杂度较高、聚类中心较难选取等问题，我们提出了以下三个方法予以解决。

(1) 通过DTW算法，改善表格相似性度量；

(2) 通过自压缩Canopy聚类，降低时间复杂度；

(3) 通过启发式聚类中心选取，提高算法自动性。

2.1.1 基于DTW的Web表格相似性度量

对于常见的经典聚类算法而言，相似性度量/距离度量是必不可少的，是决定聚类算法效果的关键。Web表格以行和列的形式组织而成，其中若干行和列在形式上是重复的，这种重复结构不影响表格形式特点，但极为影响表格的相似性度量，如传统的树编辑距离[17]、最长公共子串[18]、简单树匹配算法[19]都较难解决该问题。因此，解决重复子结构带来的问题是Web表格相似性度量的关键。

为解决问题，我们首先给出以下定义：

定义1Web表格。对于具有表格形式的显式结构，并以DOM(HTML标签树)为隐式结构的网页内容组织形式，我们称之为Web表格(Web table)。

定义2Web表格相似度。任意两个表格的DOM树的相似度Sim(Treei,Treej)，等于该两个Web表格的相似度 Sim(Tablei,Tablej)。

定义3叶子路径。DOM树的根节点到叶子节点的HTML标签序列称为DOM树叶子路径pathi。

定义4叶子路径相似度。任意两个叶子路径的相似度ψ(pathi,pathj)的计算如式(3)所示。

(3)

其中，Max(γ)=a×min{|pathi|,|pathj|}，Min(γ)=-a×min{|pathi|,|pathj|}-b×ΔL，其中ΔL=||pathi|-|pathj||。a表示字符串编辑距离的匹配操作的权重，b表示替换、插入或删除操作的权重。

接着，结合表格结构特点，我们引入一个假设：

假设1表格形式上的伸缩(重复子结构的多少)与语义结构无关[20]。

然后，我们通过对DOM树以先序遍历的方式获得叶子路径，计算任意两两叶子路径相似度。基于假设1，使用DTW[21]的方法计算两棵树的累积距离，如式(4)所示。

其中，Φ[i,j]表示一个(m+1)×(n+1)的矩阵，m和n分别表示两个表格的路径数，将Φ[i,0] 和Φ[0,j] 初始化为，Φ[0,0]=0，以及进行等价转换φ(pathi,pathj)=1-ψ(pathi,pathj)，另外，Min=min {Φ[i,j-1],Φ[i-1,j],Φ[i-1,j-1]}，因此Φ[m,n]可表示两棵DOM树的累积距离。设N为动态规整路径的节点数。

最终，可得两棵树的相似度，如式(5)所示。

2.1.2 自压缩Canopy预聚类

对于样本集，通过“相似去重”可以缩小数据集规模，消除同质化样本的集体效应，以更好地发现样本间的相互关系与存在模式，这种思想我们称之为等价压缩。

为降低聚类算法的时间复杂度，我们基于等价压缩的思想提出了自压缩Canopy预聚类方法，具体如下：

(1) 通过构造等价距离，将复杂的两个Web表格之间的DTW距离计算等价为构造的基准坐标空间下的欧氏距离计算，从而缩短单个点对的距离计算时间。

(2) 通过提出一种自压缩Canopy聚类算法进行预聚类，在聚类的过程中剔除等价表格，以降低聚类规模。在预聚类的结果下，缩小点对距离计算范围，即只计算在同一个类内的点对距离，从而减少不必要的点对距离计算。

为了“相似去重”，刻画表格等价性，我们给出了以下两个定义。

定义5等价表格。设定一个极小的数ε，ε>0，如果两个表格Tablei和Tablej的距离小于ε，那么我们认为这两个表为等价表格。因此，对于第三个表格Tablek，如果已知Tablei和Tablek的距离为dik，那么Tablej和Tablek的距离djk等于dik。

由2.1.1节内容可知，设有S个表，则所有表格DTW距离所产生的时间复杂度为ΟD((SMNmn)2)(M和N分别表示两棵DOM树的叶子路径总数，m和n分别表示两条叶子路径的长度)。通过使用等价距离，时间复杂度变为ΟD(KSMNmn)+ΟE((KS)2)(即Ο(KS)的DTW距离计算加上Ο(S2)的K维向量之间的Euclidean欧氏距离计算)，其中K远小于S，且ΟE(S2)的欧氏距离计算时间远小于ΟD(S2)的DTW距离计算时间。由以上时间复杂度分析可知，等价距离极大地缩短了单个点对的距离计算时间。

在构造等价距离之后，基于等价压缩的思想我们提出了自压缩Canopy聚类算法，如算法1所示。

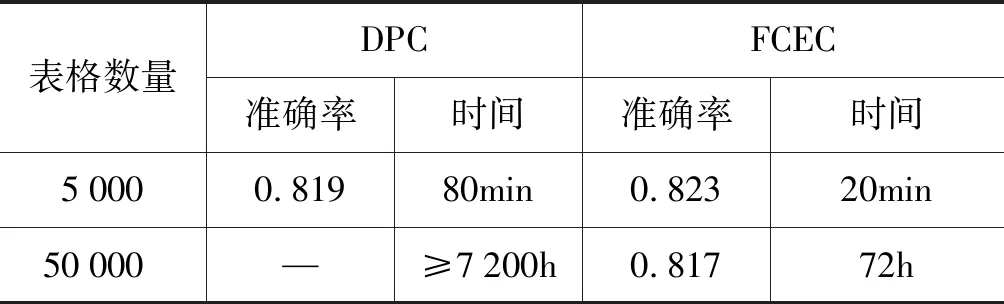
算法1 自压缩Canopy聚类算法输入: 样本集S=Xi{}Ni=1,两个距离阈值T1,T2,并且T1>T2输出: Canopyi{}Ki=1,每个Canopy包含的样本点(1) 从样本集S中随机选出一个小样本集S′=Yi{}Mi=1;(2) 调用Canopy原始聚类算法[22]求得小样本集S′的L个Canopy中心Ci{}Li=1;(3) 结合中心Ci{}Li=1在S对应的样本点,对S进行排序,将包含样本集数量多的Canopy的中心点优先处理,从而形成一个有优先处理顺序的新样本集S″,并都标记为1;(4) 从新样本集S″中依次选择一个标记为1的样本点Xj作为一个Canopyi的中心,并将其标记改为0;(5) 计算样本集S″中除Xj之外的所有标记为1的样本Xi{}Ni=1Xj到Xj的等价距离d′ij;(6) 如果d′ij<ε, 该样本Xi为Xj的等价样本(等价表格),保存该等价关系,并将该样本Xi标记改为0;如果d′ij

其中，步骤(2)、步骤(3)的目的在于通过随机构造小样本集得到一些初始预聚类中心，使得这些中心对应的样本点能在循环步骤(7)的前若干次能找到大量的等价表格，从而减少步骤(5)中距离的计算次数，即当越多的样本被标记为0时，样本规模就不断缩小，算法的执行速度加快。

通过自压缩Canopy聚类，可以得到若干个Canopy，由于Canopy预聚类旨在说明出现在同一个Canopy里的样本点才有可能被聚在同一个类[23]。因此我们只需要计算同一个Canopy里的任意样本点之间的点对距离，在满足一般的聚类过程和结果前提下，减少不必要的点对距离计算。

2.1.3 启发式聚类中心选取

在DPC算法中，聚类中心通常是那些局部密度ρi和相对距离δi都比较大的点。因此通过构造γi=ρi×δi，找出γi值比较突出的点，对于自动识别聚类中心有重要的启发式作用。由于局部密度ρi和相对距离δi可能不在一个数量级，所以为使γi值更合理，需要对ρi和δi进行归一化，如式(7)所示。

由图2可知，UCI的Aggregation和Flame数据集的γi，γi值比较突出的点分别有7个和两个(如图2中虚线上方的稀疏的圆圈所示，因为个别γi值较为接近，两图中都有两个几乎重叠的圆圈)，与这两个数据集的实际类别数保持一致。由此可见，γi值比较突出的点正是候选的聚类中心点，找出γi值比较突出的点是解决问题的关键。

图2 UCI的Aggregation和Flame数据集的γi散点图

如图2所示，γi值比较突出的点在图中较为稀疏，而不突出的点则较为密集且平滑，在某一点处发生阶跃(如图2中虚线所示)。因此确定产生“阶跃”的位置，在“阶跃”点前的所有较大的γi值所对应的点即为聚类中心点。

由上分析，我们根据聚类中心的特点，提出了启发式聚类中心选取算法，具体流程如算法2所示。

算法2 启发式聚类中心点选取算法输入: 样本集S=Xi{}Ni=1中所有样本点的局部密度ρi和相对距离δi,截断距离d′c输出: 聚类中心点Ci{}Mi=1(1) 计算每一个样本点Xi的γi值;(2) 对γi值进行降序排序,使得γq1≥…≥γqN;(3) 计算每个γqi的密度ργqi;(参考公式(1))ργqi=∑jχdγqiγqj-d′c(), dγqiγqj=γqi-γqj(4) 计算相邻两ργqi值之差Spaceqi=ργqi-ργqi-1;(5) 找出“阶跃点”位置qj～j:argmaxSpaceqj{};(6) 从前qj-1个γi找出相应样本点作为聚类中心Ci{}Mi=1;

基于自压缩Canopy聚类和启发式聚类中心选取算法，我们提出了基于等价压缩的Web表格快速聚类算法(fast clustering with equivalent compression，FCEC)，如算法3所示。

算法3 基于等价压缩的Web表格快速聚类输入: 表格样本集S=Xi{}Ni=1,截断距离dc输出: 每一个表格样本点Xi的类别标签Lj{}Kj=1(1) 对样本集S执行算法1(自压缩Canopy聚类),得到K个Canopy即Canopyi{}Ki=1;(2) 计算每个Canopy所包含的样本点的点对等价距离d′ij;(3) 计算每个样本点Xi的局部密度ρi;(4) 计算每个样本点Xi的相对距离δi;(5) 分析γi=ρi×δi,执行算法2,即通过启发式算法自动选择聚类中心点;(6) 给每个样本点Xi选择最近的聚类中心,赋予类标签Lj;(7) 计算每个类的平均密度上界ρUpK,判断每一个样本点Xi是否为离群点。

2.2 基于FCEC的表格知识抽取

通过基于FCEC的Web表格快速聚类，我们把具有相似形式结构的表格聚在一类，针对每一类，采用相应的抽取算法(模板化)进行知识抽取。

例如，对于水平表格这一类表格，我们可以依据算法4从表1中抽取出知识三元组<伊夫林卡西尔，职位，出纳员>。如表1所示，“姓名”和“职位”为属性行，由HTML的“th”标签标识，而其他行用“tr”标识，具体到每个单元格用“td”标识。对于第一列中的实体，我们可以在第二列的“职位”属性中找到对应属性值，构成“姓名→职位”的语义结构。

表1 水平表格示例

在算法4中，对于水平表格这一类型的表格来说，属性或实体关系(Predicate(k))一般出现在首行，主实体(Subject(k))出现在首列，其他列为客体或属性值(Object(k))。根据大量实验观察，过滤规则可为： 第一列为主实体列，如果第一列为字母或者数字序列，则依次向右找到第一个实体列作为主实体列。

算法4 面向水平表格的模板化知识抽取算法输入: 通过算法3聚类得到的水平表格(M行N列)输出: 三元组< Subject(k), Predicate(k), Object(k)>(1) For i=0 to M do(2) For j=0 to N do(3) if th[i=0, j] 且td[i,j=0]满足过滤规则 do P(k)‰ th[i=0, j]; O(k)‰ td[i, j]; S(k)‰ td[i, j=0];(4) End for(5) End for

3 实验与分析

为了验证所提算法的可行性和性能效果，我们采用不同类型的数据集进行实验。

(1) UCI公开数据集： Aggregation、Iris、Flame数据集；

(2) 人造Wiki数据集： 爬取50万个维基百科网页，通过Jsoup网页解析和清洗，随机选择5 000和50 000个维基表格分别作为Wiki数据集S1和S2。

实验条件和实验过程：

(1) 实验采用的硬件条件： Intel E5-2640 2.40 GHz×2，64 GB RAM；软件环境： Windows 7 64 bit，Java 1.7.0，Matlab 2014b。

(2) 实验过程： 首先在UCI数据集上验证等价距离的有效性，然后验证自压缩Canopy算法的预聚类性能，最后验证基于FCEC的表格知识抽取的效果。

3.1 等价距离的有效性

为验证等价距离在一般数据集上的有效性，我们分别对UCI的Aggregation、Iris、Flame数据集进行不同K基准点下(K=0/5/10/20)的聚类测试。其中，K=0时表示不使用等价距离，即用常见的距离计算方式进行计算，并使用DPC聚类。聚类结果如图3所示。

图3 不同K下Aggregation、Iris、Flame数据集的聚类

由图3可知，在不同的K基准下都能呈现较好的聚类形式，由于基准的不同，导致聚类的形状有所区别，存在伸缩、翻转等现象，但基本都能将各类有效区分。再者，选取哪K个基准点具有随机性，我们在K=5/10/20下分别做了20次试验，求得平均聚类准确率如表2所示。在此，我们使用准确率(正确聚类样本数/样本总数)来衡量在3个数据集上的聚类效果。

表2 不同K下的不同数据集的聚类准确率

由表2可知，对于不同的K，P值在原来的基础上上下浮动。因此，等价距离在某种程度上为了提高聚类速度对聚类准确率有所改变，但基本能达到原有的、不使用等价距离的聚类效果，还可能超越，这取决于K的基准数的选择以及基准表的选择。事实上，在实验中我们发现，如果K选择的那K个基准点正好是聚类中心时能达到比较稳定的、近似等价的聚类结果。

3.2 自压缩Canopy算法的预聚类性能

自压缩Canopy算法主要通过预聚类，在聚类的过程中剔除等价表格，以降低聚类规模，然后在构造好的Canopy集中，只计算在同一个Canopy内的点对距离，从而减少不必要的点对距离计算，并将计算好的点对距离保存，为后续的表格聚类算法提供输入。以K=20基准表进行等价距离转换，对 5 000 和50 000个Wiki表格进行自压缩后，剔除掉的等价表格占将近90%，分别剩余590和4 357个表格。这种现象可能是因为Wiki表格本身相对模板化、风格较为统一，从而导致存在大量的等价表格出现。

由于自压缩Canopy算法还需要首先设定两个超参数： 距离阈值T1，T2，在此，我们使用交叉检验的方式求得5 000个表格下的距离阈值T1，T2，如表3所示。因为T1的大小决定了样本点的重复迭代次数，影响自压缩Canopy算法时间；T2的大小决定了每个Canopy内样本点的数量，从而影响了需要计算的样本点的点对距离计算的时间。因此，对于5 000个表格，当我们选择T1=0.4，T2=0.3时，可以得到79个Canopy，且最终FCEC聚类算法所用时间为20min，且达到了最好的聚类准确率0.823。而使用DPC聚类实际所用时间为72h(主要为计算5 000个样本点任意点对之间的DTW距离所用时间)。

表3 对超参数T1,T2(T1>T2)的交叉验证

其中，79个Canopy意味着平均每个Canopy有5 000/79个点，因此，每个Canopy内的点对计算量为5 000/79×(5 000/79-1)×1/2≈1 971次，所有Canopy内的点对计算量为1 971×79≈155 728次，考虑等价距离、自压缩效果和重叠部分的不重复计算等因素，总计算量将远小于原始计算量的5 000×(5 000-1)×1/2=12 497 500次。同样地，对于50 000个表格，FCEC聚类算法所用时间为80min，而使用DPC聚类实际所用时间预计为7 200h左右，如表4所示。

表4 不同数据量下两算法的聚类准确率与时间消耗比较

由表4可知，在不同的数据量下，两个聚类算法的聚类平均准确率接近，但在时间性能上，FCEC聚类有明显的大幅度提升。可见，通过自压缩Canopy算法，大幅度减少了样本点点对距离计算时间，为实现大规模表格聚类提供了可操作的可能。

3.3 基于FCEC的表格知识抽取的效果

通过对5 000和50 000个Wiki表格执行基于等价压缩的Web表格聚类(算法3)，分别得到自动确定聚类中心的决策图和聚类效果图，如图4所示。图4中可见，不同灰度的点代表样本点形成的不同的簇，簇与簇之间有所区分，当选择K=20时，二者的平均聚类准确率分别为82.3%和80.5%。对于每一个簇，我们随机选择50个样本点，并统计被归属到该簇但事实上并不属于该簇的样本点(已识别的离群点不计算在内)。聚类准确率如式(8)所示。

图4 聚类中心决策图和聚类效果图(N=5 000和50 000)

由于表格聚类效果直接影响表格知识抽取算法的结果，如果不通过聚类而直接执行算法4抽取知识三元组，平均抽取准确率不超过10%。而基于FCEC聚类的表格知识抽取后，通过随机选取100个Wiki表的知识三元组抽取结果，可得所抽取的知识三元组的准确率为67.3%，在不依赖良好的表格结构和足够的先验知识的情况下，该抽取方法达到了令人满意的结果，且从对不正确的知识三元组的分析来看，尚有可提升的空间[24]。

不正确的知识三元组主要有以下三种情形：

(1) Case 1 (35%)： 表格聚类错误。聚类后的水平表格里含有少数标题或多级表头的表格，而不是如表1中所示的纯粹的水平表格。如表5所示Predicate (“2011”) 和 (“1970”) 需要相应地加上表格标题 (“人口数量最大的十个大都市区的人口” 和 “亚利桑那人口的种族比例”) 才具有一定的意义，但其中的概念属性关系获取较为复杂，是表格知识抽取的难点之一。

(2) Case 2 (33%)： 主体不出现在表格内，它可能是维基条目名称或出现在表格上下文的小标题中。如表5所示，Subject (“葡萄牙语”) 需要该表的上文小标题(“印尼语起源”)结合, 而Subject (“Jennifer Lewis”) 需要该表的上文小标题(“杜克女子足球项目获得的NSCAA全美荣誉”)，这类情况主要因为主实体属于表格下文中的父类概念下的子概念或整体与部分关系。类似地，Subject (“US Billboard Adult Top 40”) 属于该表所在的维基主题 (“拯救我 (Remy Zero歌曲)”)的子属性。和Case1相似，这类情况涉及表格上下文的非结构化文本数据，目前尚未有理想的解决方案。

表5 知识三元组示例

4 总结

针对大规模Web表格数据，本文主要通过改善Web表格相似性度量、降低时间复杂度、自动判断聚类中心三个方面，提出了一种基于等价压缩的Web表格快速聚类算法，用以发掘表格的形式结构类型与特点，然后从相似形式结构的表格中推测表格的语义结构，从而在模板化的结构中抽取知识，最终形成一套基于FCEC的Web表格知识抽取方法。从实验效果上看，在保证聚类准确率的前提下，新方法相比原始方法在时间效率上有大幅度提升，在表格聚类后利用表格模板所抽取的知识三元组的准确率也达到了令人满意的结果，但在结合NLP方法提高所抽取的知识三元组的准确率上仍有较大的提升空间。

此外，对于超大规模的Web表格，所提算法仍具有局限性，因此如何将所提算法进行分布式计算以更快的速度处理超大规模数据值得探讨。