蕉园自走式压穴施肥机设计与试验
2019-05-24张卓伟金莫辉孙健峰
杨 洲,张卓伟,李 君,金莫辉,孙健峰
(华南农业大学 工程学院,广州 510642)
0 引言
香蕉是我国5大经济粮食作物之一,主要产区分布在云南、海南、广西、广东和福建等省份。2014年,我国香蕉种植面积为39.55万hm2,总产量达到1 179.19万t,总产量和消费量均居世界第二位[1]。香蕉施肥主要采用撒施肥、穴施肥、沟施肥、喷灌及滴灌等方式[2-8]。其中,喷灌与滴灌主要用于施用液体肥料。撒施肥容易造成肥料的浪费,受降雨天气的影响[9];沟施肥作业效率高,但容易破坏香蕉根系致其发病,不利于香蕉的长期生长[10~12];穴施肥作业灵活,对香蕉根系影响小,易于实现科学施肥。目前,我国蕉园的穴施肥机械基本是便携式穴施机,人工劳动强度大[5],因此开发一种适合蕉园穴施肥的高效作业机械,对于推动我国香蕉产业的发展有着重要的意义。本文基于可变位、变深、变量施肥的设计要求,采用压穴施肥的作业方式,对蕉园自走式压穴施肥机的关键部件和液压系统进行设计,通过开展压穴性能试验和排肥稳定性研究,并进行主要作业参数和试验指标之间的多元回归分析,以期为蕉园变量穴施肥作业提供参考依据。
1 整机结构及工作原理
蕉园自走式压穴施肥机主要由发动机、机架、电控箱、液压系统、压穴机构及施肥机构等组成,如图1所示。工作时,控制电控箱驱动蕉园自走式压穴施肥机行驶至作业位置,进行压穴施肥作业;在此过程中,控制系统控制压穴机构与施肥机构实施变深、变位、变量施肥。
蕉园种植的窄行1.2~2.0m,宽行约4m,株距1.8~2.5m ,施肥深度200~400mm[10-11,13]。为保证施肥机在蕉园的通过性,施肥机纵向和侧向外形尺寸应小于1.2m,结合施肥农艺的要求确定施肥机的压穴深度应在0~400mm区间可调[3-4,9-10]。设计的蕉园自走式压穴施肥机主要参数,如表1所示。
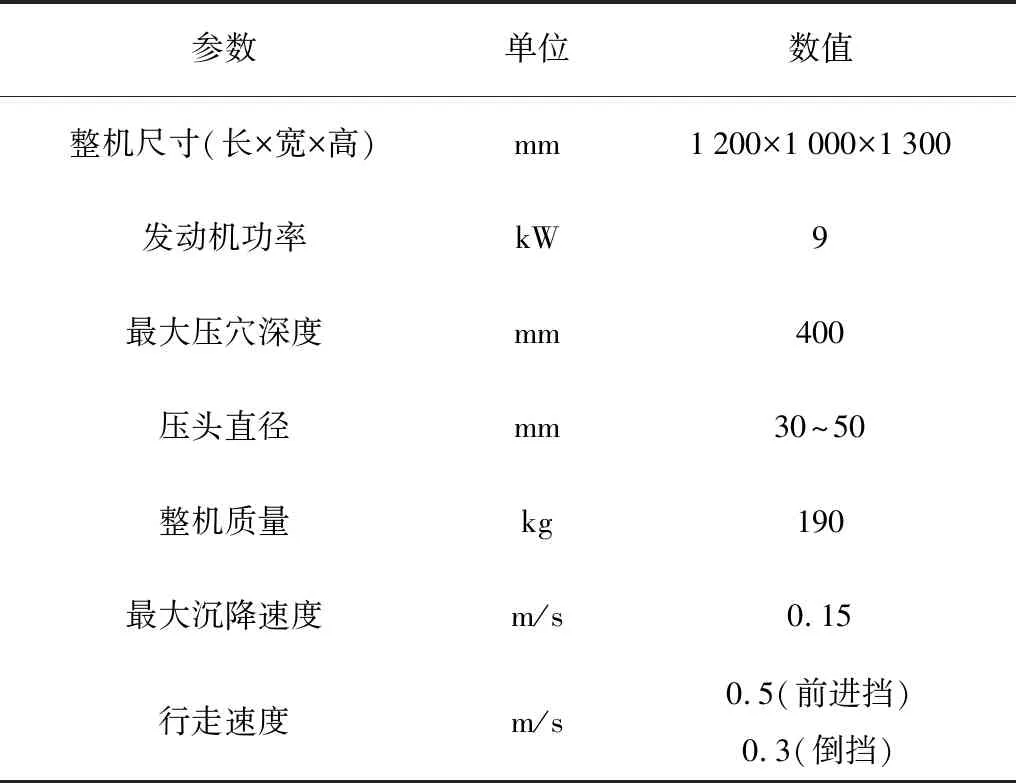
表1 施肥机主要参数Table 1 Main parameters of fertilizer applicator
2 关键部件设计
2.1 压穴机构设计
为实现变深与变位施肥功能,将压穴部件设计成具有垂直和水平方向二自由度平移运动的机构,如图2所示。
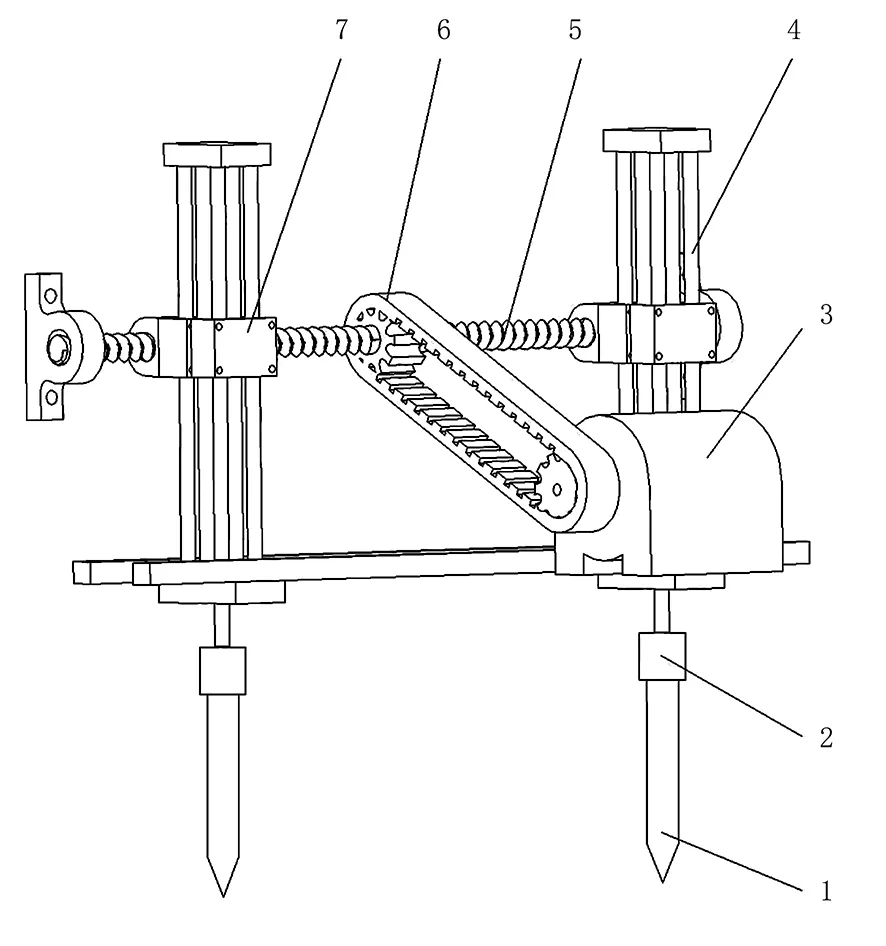
1.压头 2.转接螺母 3.液压马达 4.液压缸 5.双向丝杆 6.皮带 7.滚动轴承图2 压穴机构示意图Fig.2 Structure diagram of punching mechanism
压头与液压缸通过转接螺母连接,两液压缸通过螺钉分别固定在双向丝杠的两个丝杆螺母上,液压马达与双向丝杠通过带传动连接。液压缸驱动压头在垂直方向上实现变深的压穴运动,而双向丝杠可实现压头在水平方向的变位。香蕉最大单次施肥量为2.0kg/株[3-5,10-11],肥料颗粒密度在900~1 200g/cm3区间。基于香蕉栽培模式特征、施肥农艺技术要求及施肥机的结构尺寸,确定压头直径范围为30~50mm,长度取400mm。
2.2 施肥机构设计
施肥机构是实现精量施肥的关键,其结构如图3(a)所示。施肥箱固定于机架,电机通过转轴连接外槽轮排肥器,施肥管连接施肥套筒与外槽轮排肥器。在施肥作业时,电机根据预设的压穴深度,实施定量排肥的精准控制。
根据排肥原理,外槽轮每转的排肥量q1按下式计算,即
(1)
式中d—外槽轮外径(cm);
L—槽轮的有效工作长度(cm);
γ—肥料密度(g/cm3);
α0—槽内肥料充满系数;
fq—单个凹槽的截面积(cm2);
t—槽轮凹槽节距(cm),t=πd/z,z为槽数。
λ—带动层特性系数。
fq可由槽轮的几何图形求得,如图3(b)所示。圆弧形凹槽截面积计算式为
(2)
根据施肥机0.15m/s的沉降速度、压穴深度100~400mm、施肥机作业位置2~4个/株(即8~16个洞穴每株),以及香蕉的养分需求[13,16,18],结合外槽轮排肥器的标准尺寸,代入式(1)计算。取外槽轮外径d为61.6mm,槽数z为6,凹槽半径为9~14mm,槽轮的有效工作长度L为63mm,电机的工作转速40~100r/min。
2.3 液压系统设计
液压系统由液压工作站及电控系统组成。液压工作站的执行元件有3个液压马达及2个液压缸,每个执行元件均可单独工作。液压回路如图4(a)所示,参数如表2所示。电控系统如图4(b)所示,核心控制器选用了三菱PLC Fx3U。系统通过触摸屏进行参数化设置,PLC根据给定的操纵指令和传感器反馈信息,通过控制马达转速、液压比例换向阀电流及电磁阀通断,实现施肥机进退、液压缸升降和双向丝杠正反转等功能。
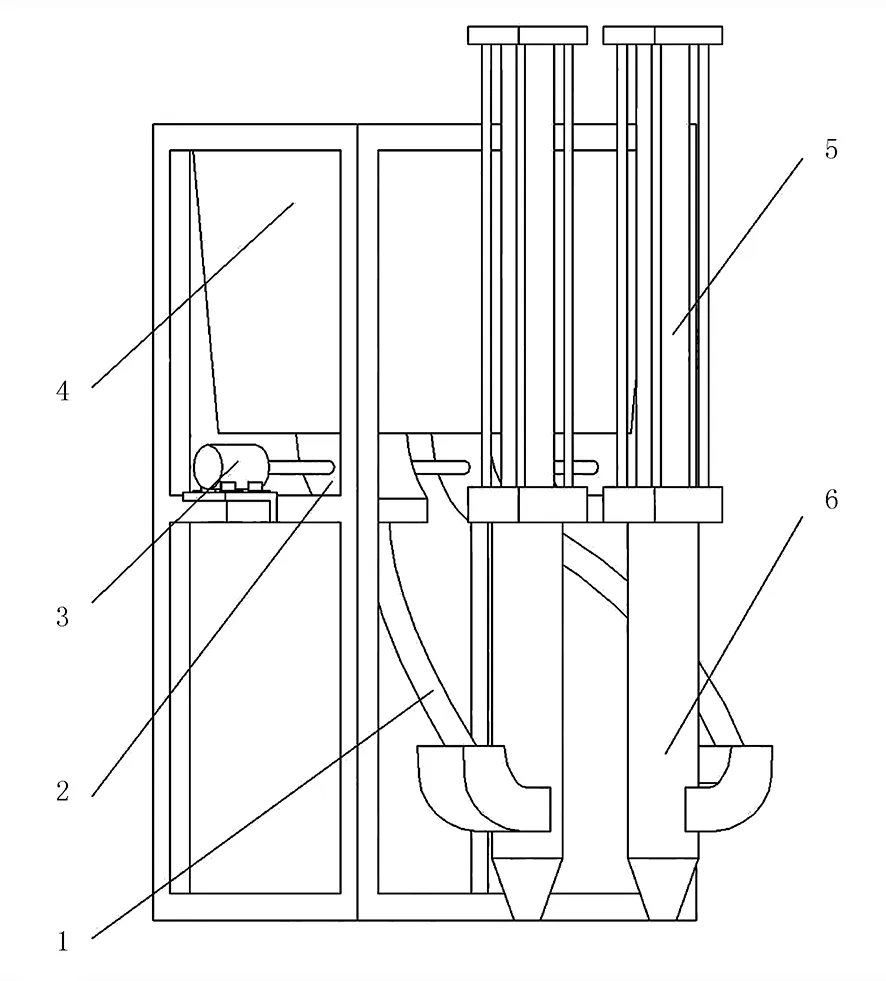
1.施肥管 2.外槽轮排肥器 3.电机 4.施肥箱 5.液压缸 6.施肥套筒 (a) 结构示意图

(b) 外槽轮凹槽断面图3 施肥机构Fig.3 Fertilizing mechanism表2 液压系统参数Table 2 Parameters of hydraulic system

参数单位数值工作压力MPa24流量m3/s24液压缸活塞杆直径mm18液压缸最大下降速度m/s0.15油管直径mm6油箱容积m30.05

1.发动机 2.液压油箱 3.液压泵 4.溢流阀 5.两位两通电磁阀 6.两位四通电磁阀 7.液压马达 8.液压比例换向阀 9.液压缸 (a) 液压回路
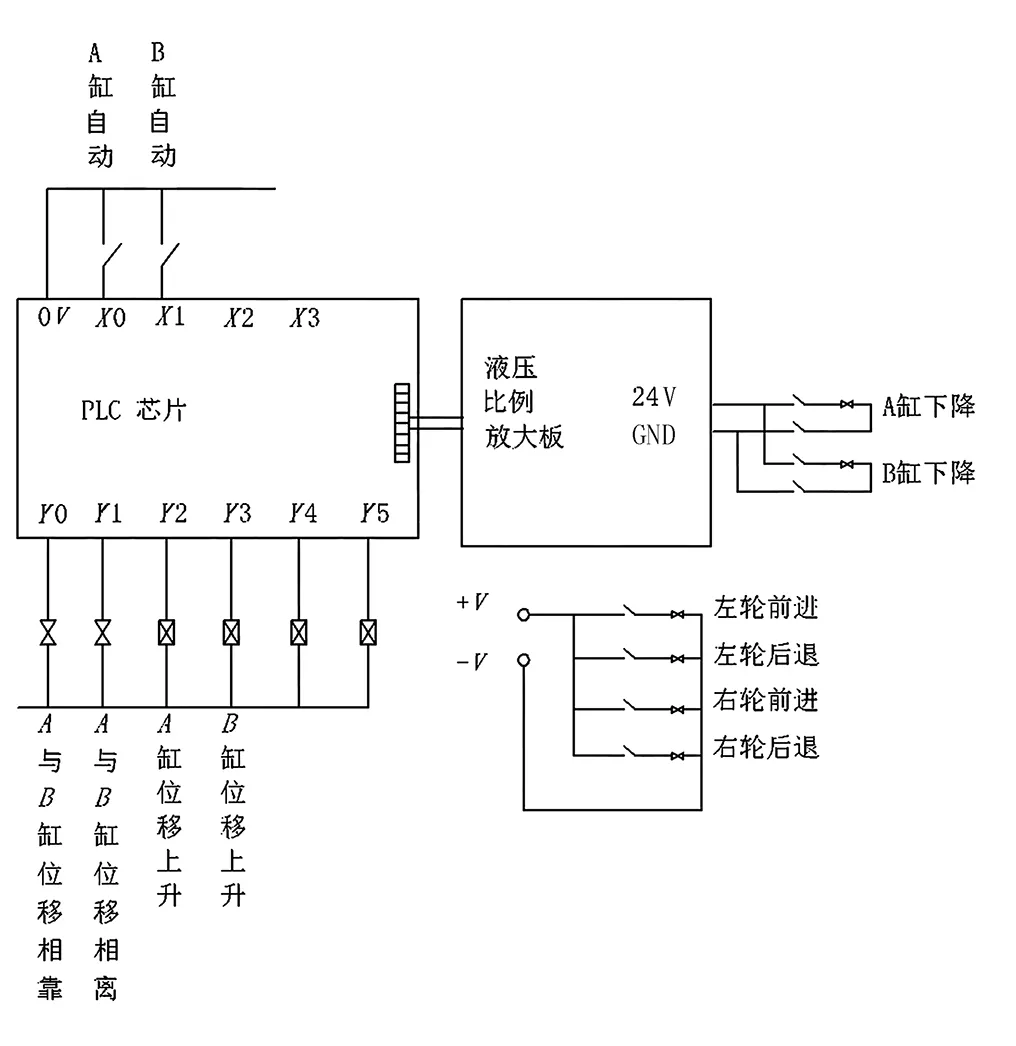
(b) 电控系统图4 液压系统Fig.4 Hydraulic system
3 压穴性能试验与排肥稳定性试验
试验仪器与设备:土槽试验台(华南农业大学工程学院试制)、拉压力传感器(北京龙鼎金陆测控技术有限公司LDCZL-Z型,500kg)、位移传感器(北京龙鼎金陆测控技术有限公司LDPS-L型,0~2000模拟)、重量变送器(北京龙鼎金陆测控技术有限公司LDST-I(V)-SP型,0~10V)、数据采集卡(研华USB-4711A,100ks/s)、土壤硬度计(浙江托普仪器有限公司TYD-2型)、土壤湿度检测仪(浙江托普仪器有限公司TZS型),以及夯实机(上海嘉本园林设备有限公司90T汽油嘉陵本田型)。蕉园自走式压穴施肥机(华南农业大学工程学院试制)、电子天平(北京赛多利斯仪器系统有限公司ALC-210.3型)、非接触式转速计(东莞市耀锋电子设备有限公司SM2234A型)、PVC管(φ80×500),以及收纳盒(300×180×100)。
3.1 压穴性能试验
施肥效率是衡量压穴施肥机性能的重要指标,施肥效率与峰值压穴阻力密切相关,因此采用峰值压穴阻力作为压穴功耗的评价指标,优化压头结构,并构建多元线性回归模型,为压穴作业提供决策依据。试验测量方法:用土壤硬度计与土壤湿度检测仪监测土壤,翻整土槽试验台中的土壤并用夯实机夯实多次,使土壤硬度在300~380N、含水率在20%~25%区间范围内;启动蕉园自走式压穴施肥机进行压穴作业,通过上位机采集压穴过程中的位移和压力,每处理重复6次。
压头沉降过程的受力曲线如图5所示。由图5可知:压穴过程中的压穴阻力主要来自压头的端部压力;端部压力在初始阶段与深度呈正相关关系,当端部压力到一定值后趋于稳定;压穴过程初始阶段,压头基本没有摩擦阻力,但沉降一定深度后,摩擦阻力与深度呈正相关关系。
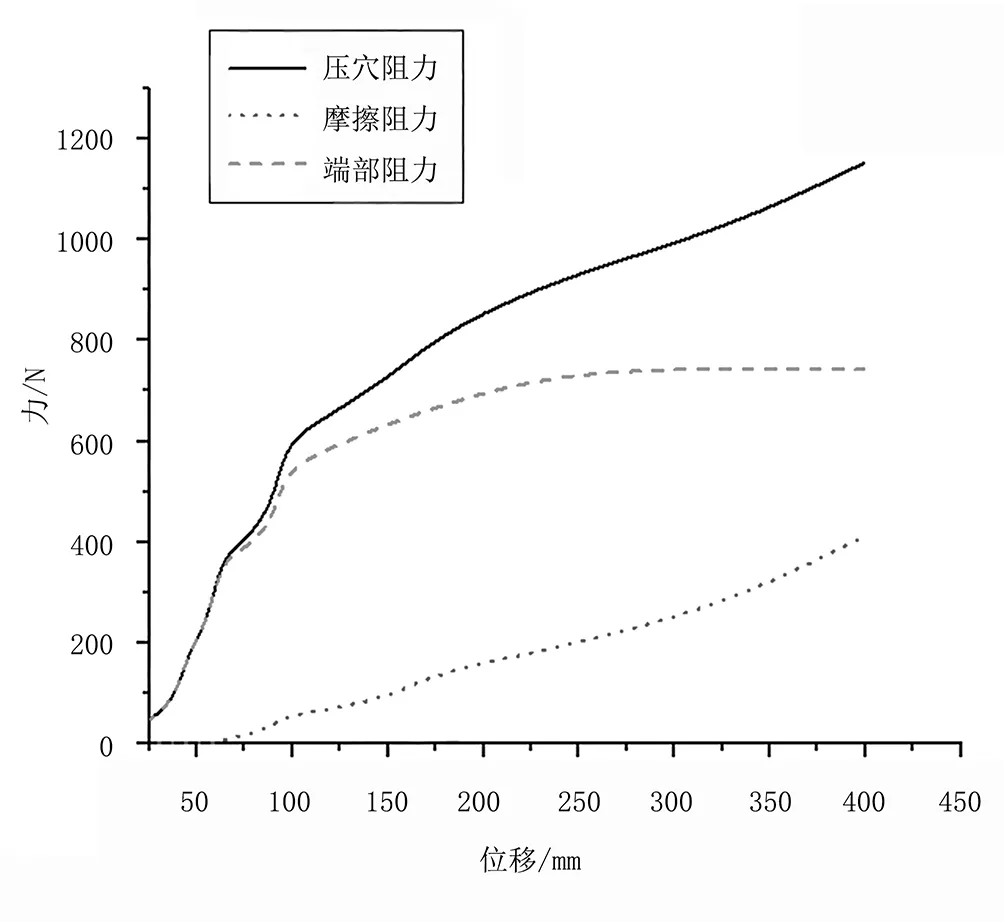
图5 压头沉降过程受力曲线Fig.5 Force curves of punching head in falling process
3.1.1 单因素试验
以压穴阻力峰值为指标对压头直径进行单因素试验,试验时沉降速度0.15m/s,压头锥度40°。试验结果如图6(a)所示。由图6可以看出:峰值压穴阻力与压头直径呈正相关性。方差分析结果表明:压头直径对压穴阻力峰值有极显著影响(sig.<0.01)。
以压穴阻力峰值为指标对压头锥度进行单因素试验,试验沉降速度0.15m/s,压头直径30mm。试验结果如图6(b)所示。由图6可知:峰值压穴阻力与压头锥度呈正相关性,减少锥度能有效降低施肥机作业能耗。方差分析结果表明:压头锥度对压穴阻力峰值有极显著影响(sig.<0.01)。
以压穴阻力峰值为指标对压头沉降速度进行单因素试验,试验时压头直径30mm,压头锥度40°。试验结果如图6(c)所示。方差分析结果表明压头沉降速度对压穴阻力峰值无显著影响(sig.>0.05)。
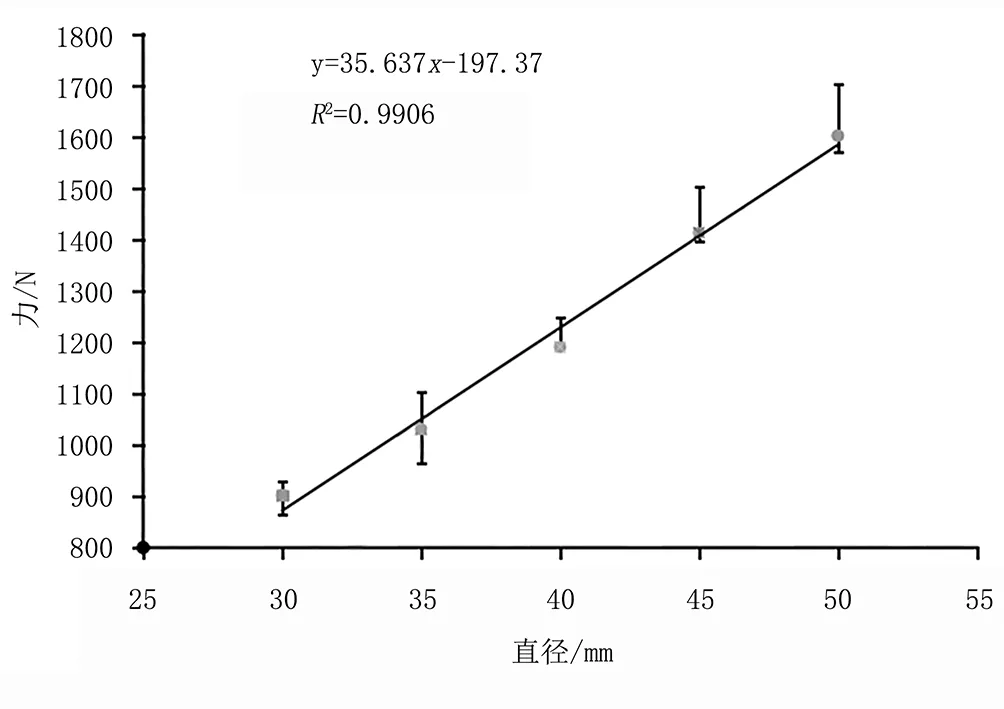
(a) 压头直径

(b) 压头锥度
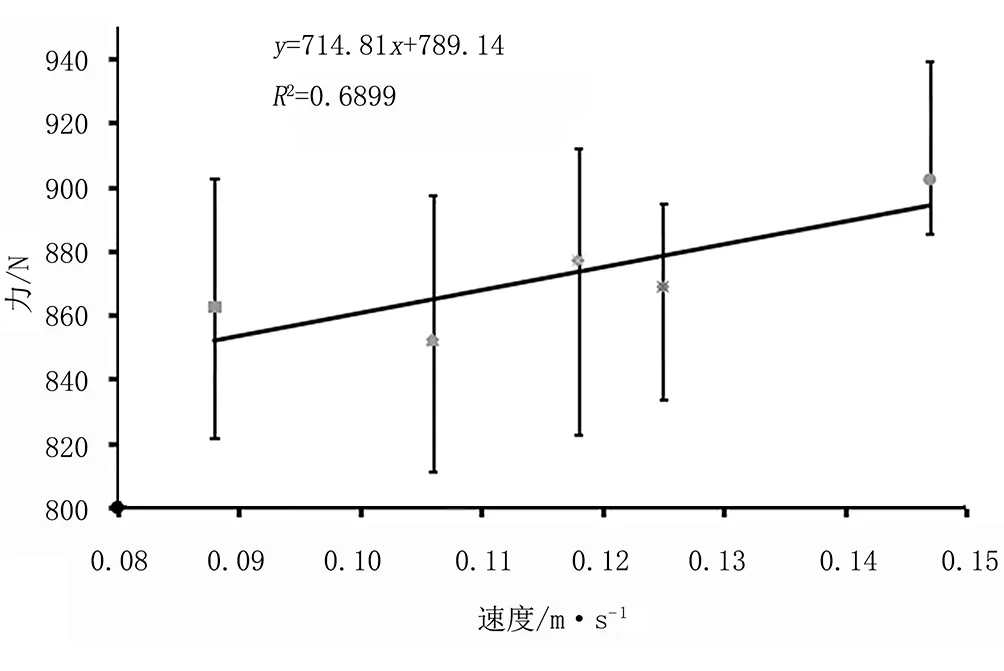
(c) 沉降速度图6 峰值压穴阻力单因素试验结果Fig.6 Single factor test results of peak punching resistance
3.1.2 多元回归试验
单因素试验结果表明:压穴阻力峰值受压头直径、压头锥度的影响极显著,而压头沉降速度对峰值压穴阻力无显著影响;基于施肥效率最大化的要求,确定压头锥度40°和压头沉降速度0.15m/s为压穴机构的最佳参数组合。以峰值压穴阻力y为试验指标进行回归试验,试验结果如表3所示。
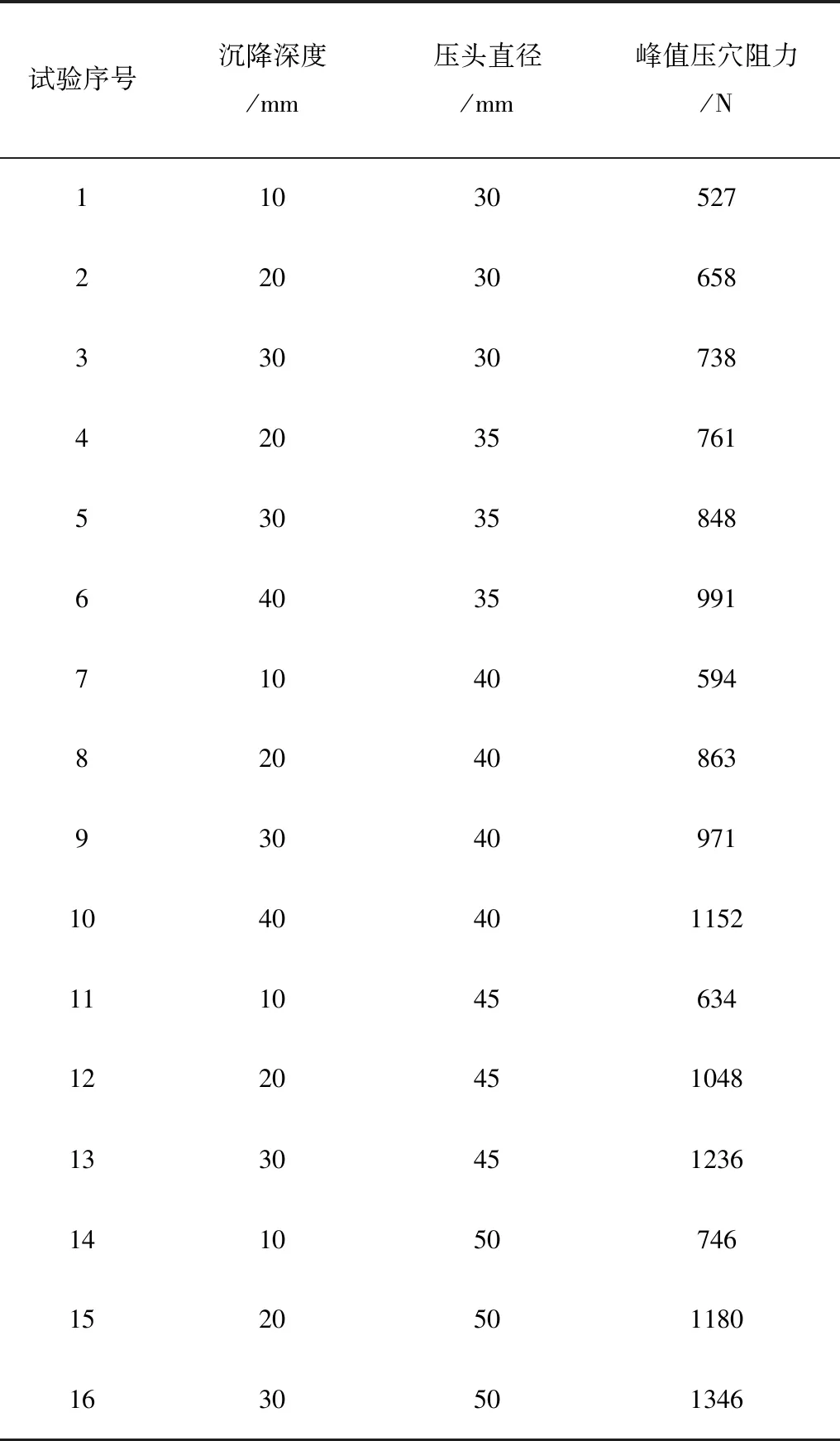
表3 回归试验结果Table 3 Regression test results
采用SPSS软件进行回归分析,计算得峰值压穴阻力在因素空间范围内的回归方程,即
y=18.227x1+23.752x2-478.254
(3)
其中,x1为沉降深度(mm);x2为压头直径(mm);相关系数R2=0.873。
实际施肥过程中,可根据香蕉植株的施肥量要求以及施肥机的载重状况,由式(3)选定不同沉降深度和压头直径组合,进而完成变深、变位和变量施肥的参数组合决策。
3.2 排肥稳定性试验
排肥稳定性是衡量施肥机作业效果的重要指标。排肥稳定性试验采用排肥量的变异系数作为评价指标,用于描述在相同工作条件下排肥量的变异程度。试验方法:启动蕉园自走式压穴施肥机进行压穴施肥作业,使压穴机构的压头下降直至穿过收纳盒,施肥机构的电机按预设的转速与时间转动将定量的肥料排出并积于施肥套筒内,压穴压头抬起使肥料落入PVC管内,如图4所示。记录落入PVC管内肥料的质量,每处理重复6次。
变异系数的计算公式为
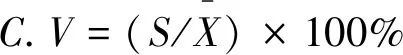
(4)
其中,C.V为变异系数(%);S为样本施肥量标准差(g);X为样本施肥量平均值(g)。
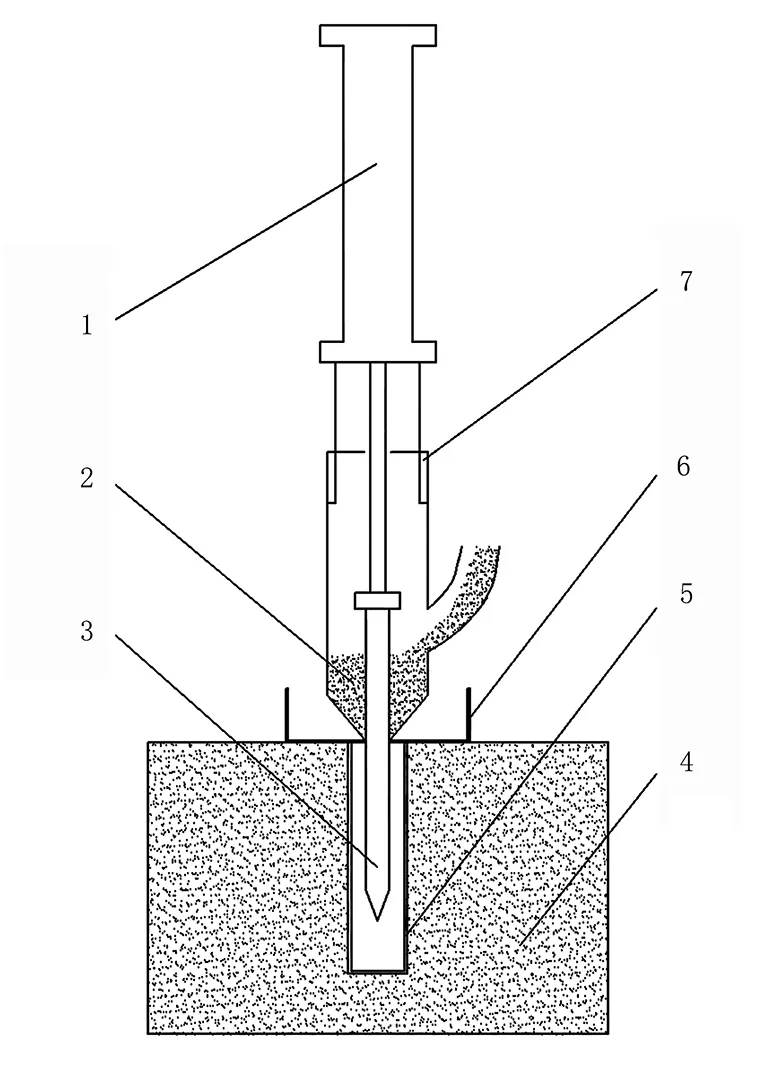
1.液压缸 2.肥料 3.压穴压头 4.土壤 5.PVC管 6.收纳盒 7.施肥套筒图7 施肥试验原理图Fig.7 Schematic diagram fertilizing test
由文献[14-18]可知:外槽轮转速、排肥量和螺旋升角均对排肥器的排肥变异系数有显著影响。为研究施肥机的排肥稳定性,进行了三元一次回归正交试验,试验的水平编码表如表4所示,结果如表5所示。
用SPSS软件进行回归分析,计算得施肥量变异系数的回归方程为
y=5.907+1.3x2-6.35x3-0.625x1x2-
1.35x1x3-0.325x2x3
(5)
其中,x1为外槽轮转速(r/min);x2为施肥量(g);x3为外槽轮螺旋升角(°)。
当施肥量与外槽轮参数一定时,根据式(5)可确定施肥稳定性最佳的电机转速,从而为施肥的决策提供参考。

表4 因素水平编码表Table 4 Coding of factors and levels
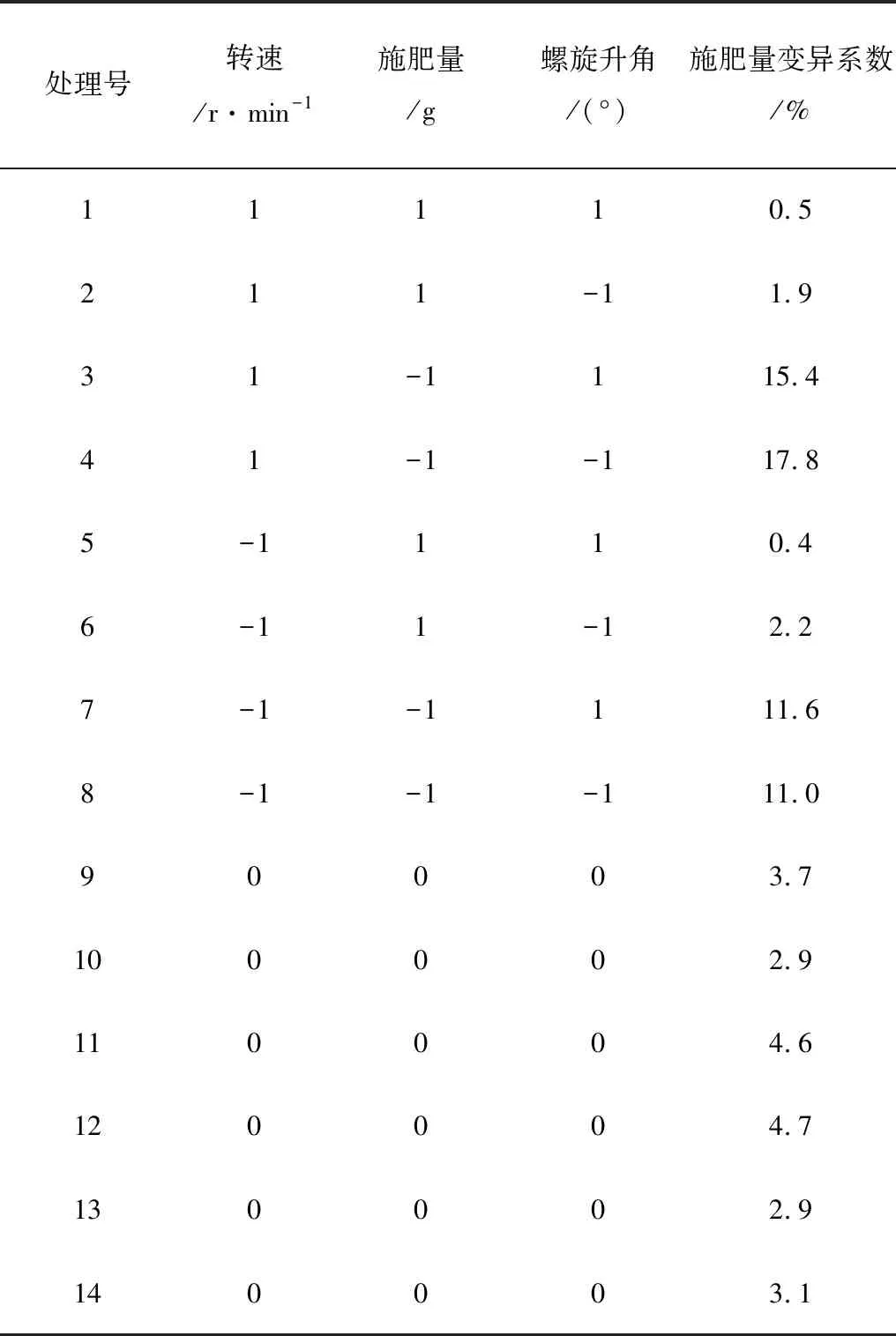
表5 回归试验方案及结果Table 5 Scheme and results of regression test
4 结论
1)压头的直径和锥度均对峰值压穴阻力的影响极显著,呈正相关关系,减少锥度能有效降低施肥机作业能耗。
2)峰值压穴阻力与沉降深度、压穴压头直径之间的关系式为
y=18.227x1+23.752x2-478.254
3)施肥量变异系数与外槽轮转速、外槽轮螺旋升角、施肥量之间的关系式为
y=5.907+1.3x2-6.35x3-0.625x1x2-
1.35x1x3-0.325x2x3
