基于RVM的配比变量排肥掺混均匀度离散元仿真及验证

苑 进，辛振波，牛子孺，李 扬，刘兴华，辛 帅，王建福，汪力衡



基于RVM的配比变量排肥掺混均匀度离散元仿真及验证

苑 进，辛振波，牛子孺※，李 扬，刘兴华，辛 帅，王建福，汪力衡

（山东农业大学机械与电子工程学院，泰安 271018）

采用试验测量或现有的间接标定方法很难实现配比变量排肥离散元仿真的参数标定，针对此标定难题，该文提出一种基于肥料掺混均匀度-仿真参数相关向量机模型主动寻优的标定方法。将配比变量离散元排肥过程看作特定的非线性系统，采用相关向量机机器学习方法揭示模型参数与肥料掺混均匀度之间的映射关系，建立回归元模型；基于最优模型参数值对应的肥料掺混均匀度值应与试验值一致，采用建立的元模型结合试验统计结果构建适应度函数；基于约束最优的数学思想建立数学模型，通过最优参数值遗传算法迭代计算，得到最优值。5种排肥转速下（30、40、50、60、70 r/min），排肥器采用碰撞边缘为外凸曲线形的A型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为6.4%，磷肥为4.1%，钾肥为5.9%；标定前氮肥为26.8%，磷肥为28.9%，钾肥为36.1%。采用碰撞边缘为直线形的B型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为5.8%，磷肥为5.6%，钾肥为4.9%；标定前氮肥为21.9%，磷肥为32.5%，钾肥为28.9%；采用碰撞边缘为内凹曲线形的C型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为5.0%，磷肥为3.7%，钾肥为8.7%；标定前氮肥为36.2%，磷肥为31.6%，钾肥为24.4%，该方法能够实现配比变量排肥离散元仿真参数准确有效的标定。

肥料；标定；离散元方法；配比变量排肥；相关向量机；遗传算法

0 引 言

配比变量施肥技术[1-5]考虑土壤肥力的非均匀性，实时配比调整不同种类肥料的施肥量，并实现肥料的均匀掺混，最大程度地满足各类农作物的实际需求，最大限度减少肥料浪费以及过度施肥造成的环境污染。

采用离散元技术[6-15]（discrete element mothod, DEM）建立颗粒肥料撒肥模型可以实施与耗时、费力的试验相匹配的排肥仿真，有效揭示试验无法分析的肥料颗粒微观动力学行为，厘清颗粒之间的动态掺混机理以及排肥时滞等特性，达成从微观机理层面提出施肥机具的最优设计方案。配比变量排肥离散元模型参数（物料本征参数：泊松比、密度、剪切模量以及物料接触参数：碰撞恢复系数、静摩擦系数、动摩擦系数）的标定是建模过程中的重点、难点问题。项目组前期建立的配比变量排肥模型[16-17]仿真结果与真实排肥试验结果存在较大差异，分析发现不正确参数值的采用导致了仿真不能再现真实肥料颗粒的流动行为，模型发生了失真现象。

目前，离散元模型参数标定方法主要有试验测量法和间接标定法。试验测量法通过开展物理试验，直接测定参数值。黄小毛等[18]采用弹跳试验分别对不同含水率的小麦和油菜的恢复系数进行了测定；韩燕龙[19]采用颗粒板法测量了稻谷种间静摩擦系数；González- Montellano等[20]的研究表明，对于球形度高、质地均匀的颗粒，采用直接测量能够较精确地获得微观参数值，但是对于玉米及橄榄核这类外形不规则的颗粒材料，直接测量值变化很大。针对肥料颗粒，目前尚未有测量颗粒间滚动摩擦系数的有效方法[21]，采用颗粒板法测量肥料颗粒间静摩擦系数时，会出现弹跳、碰撞等无法避免的现象，精度难以保证。

间接标定法实施与试验相匹配的离散元仿真，将模型参数作为宏观层面上颗粒团特定动力学行为的调整参数，在待标定参数经验取值域中反复取值，直到仿真颗粒团动力学行与试验现象一致，完成标定。Coetzee等[22]采用剪切和侧限压缩试验对玉米种子的摩擦系数和刚度系数进行了标定；Ucgul等[23]通过休止角和贯入度试验分别标定了土壤干、湿颗粒离散元模型的摩擦系数和恢复系数；王云霞等[24]通过对玉米种子堆积角试验数据回归分析，建立数学模型求取了种间静摩擦系数和滚动摩擦系数。刘凡一等[25]根据Box-Behnken试验结果，建立了模型参数与休止角之间的回归模型，求解得到小麦颗粒之间的接触参数值。上述间接标定方法采用“尝试法”或者二次多项式回归，不适用于多参数值待标定且非线性程度较高的配比变量排肥离散元模型。

本文针对配比变量排肥离散元模型参数标定问题，使用EDEM软件，匹配配比变量排肥试验建立离散元模型；进行了参数敏感度分析，仿真计算了经验值域内单一参数取值变化后对肥料掺混均匀度值的影响程度，确定了影响较大的主因参数；采用相关向量机[26-30]（relevance vector machine，RVM）机器学习方法揭示主因参数与肥料掺混均匀度之间的非线性隐函数关系；以试验与仿真排肥掺混均匀度的逼近程度，构建适应度函数，采用遗传算法（genetic algorithm，GA）主动寻优计算主因参数的最优值；通过试验与仿真误差分析验证方法的有效性，以期为配比变量排肥离散元模型的参数标定提供参考。

1 排肥标定试验

1.1 试验装置与仪器

于2018年6月在山东农业大学农业机械化及其自动化实验教学中心进行试验。试验辅助设备为黑龙江省农业机械研究院研制的JPS-12型综合性能检测试验台，排肥装置固定在安装架上，通过试验台控制电机带动传送带模拟排肥装置与地面的相对运动（图1）。

1. 肥箱 2. 外槽轮排肥器 3. 落肥管 4. B型掺混腔 5. 排肥管 6. 肥料传送带 7. 控制器

试验用配比变量排肥装置由3个肥箱、3个由直流电机驱动的外槽轮排肥器、3根落肥管、1个B型掺混腔[17]、1个排肥管、肥料传送带以及排肥控制器组成，如图1所示。3根落肥管居中一根的长度为450 mm，内径为36 mm；排肥管为波纹管，轴向截面为三角形波浪纹，三角波纹高度为8 mm，内径为36 mm，外径为45 mm，长度为480 mm。试验用肥箱、外槽轮排肥器、掺混腔均为亚克力材质，落肥管和排肥管为PVC材质，传送带材质为橡胶。

以山东农业大学研制的氮磷钾固体包膜控释肥作为试验用肥。试验时，3种肥料放置于不同肥箱内，采用AQMH3615NS直流电机驱动模块，控制3个排肥器外槽轮转速均为50 r/min，排肥器肥舌开度设定为最小，传送带的速度设定为0.6 m/s，排肥后肥料经落肥管下落到达掺混腔内，碰撞掺混后的肥料颗粒经由排肥管下落到肥料传送带，形成排肥带。试验发现采用上述工况多次排肥后，肥料掺混均匀度值较为一致，排肥稳定性较好，有利于开展模型参数标定。

1.2 评价指标测定

本文将肥料掺混均匀度作为配比变量排肥效果的评价指标[17]。在肥料传送带上，预先按照9列多行划分大小相同的统计单元格（70 mm×50 mm），将排肥槽轮启动后2 s确定为统计初始时刻，将此时刻后传送带上的9列20行统计单元格为统计区域。将统计单元格内某种肥料颗粒数与总颗粒数的比值，作为此种肥料当前单元格配比P：

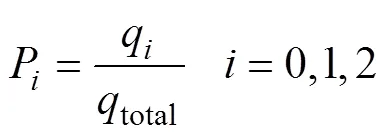
式中q为单元格中某种肥料颗粒数，total为单元格中颗粒总数。=0,1,2分别表示氮肥、磷肥及钾肥。统计区域内某种肥料颗粒数与总颗粒数的比值，作为此种肥料的目标配比V：

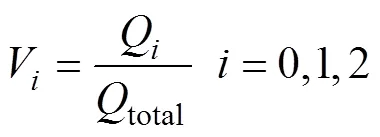
式中Q为统计区域中某种肥料颗粒数，total为统计区域中颗粒总数。某种肥料各个统计单元格配比与此种肥料目标配比的比值，作为统计单元格配比偏离度W：

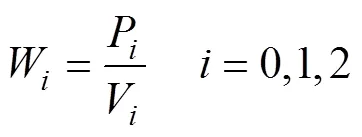
将某种肥料相对应的180个配比偏离度值取标准差，得到此种肥料的配比标准差，定义为肥料掺混均匀度，表示各统计单元格肥料配比偏离度与此种肥料目标配比的总体偏离程度，其值越小表征肥料的掺混及播撒越均匀。

试验后采用人工计数，统计各个单元格及统计区域内的3种肥料的颗粒数，按照式（1）~（3）计算3种肥料的掺混均匀度值；试验重复5次，取平均值，掺混均匀度统计结果为：氮肥为0.431、磷肥为0.758，钾肥为0.542。

2 参数标定方法

2.1 离散元模型

使用Solidwoks建立与试验用配比变量排肥器结构参数相同的模型后，以.igs格式导入到EDEM中，生成一个长为2 000 mm、宽为700 mm的几何平面模拟传送带，设置排肥器外槽轮为旋转运动，设置传送带为直线平动。

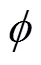
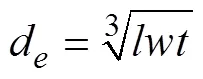
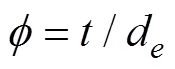
式中、、分别为肥料颗粒的长、宽、厚，且>>。氮肥颗粒等效直径分布在2.87～4.43 mm，磷肥颗粒等效直径分布在3.86～5.41 mm，钾肥颗粒等效直径分布在3.52～5.18 mm。3种肥料的平均球形率均在80%以上，较高的球形率适于采用球形颗粒建模。使用EDEM颗粒工厂功能，在3个肥箱中分别生成3种肥料的球形仿真模型，每个肥箱中生成30 000粒，直径设定为测量得到的3种肥料的平均等效直径：氮肥3.63 mm、磷肥4.65 mm、钾肥4.34 mm，通过选择EDEM中的颗粒Random分布并设定分布系数实现球形仿真模型直径为一定范围的随机分布，分布系数上限为肥料中最大等效直径与等效直径均值的比值，下限为最小等效直径与等效直径均值的比值，分布系数为：氮肥（0.79～1.22）、磷肥（0.83～1.16）、钾肥（0.81～1.19）。建立的配比变量排肥离散元模型，如图1b所示。

肥料颗粒表面无黏附作用，所以模型中肥料之间、肥料与排肥机具之间以及肥料与传送带之间均采用Hertz-Mindlin无滑动接触力学模型。模型的部分参数初始值参考前期研究[16-17]，其余参数初始值根据工程经验给出，如表1所示。以20%的Rayleigh时间步长作为仿真计算步长。匹配排肥试验掺混均匀度统计方法，采用EDEM后处理模块，在虚拟传送带上划分统计单元格，统计肥料颗粒数目，计算掺混均匀度。

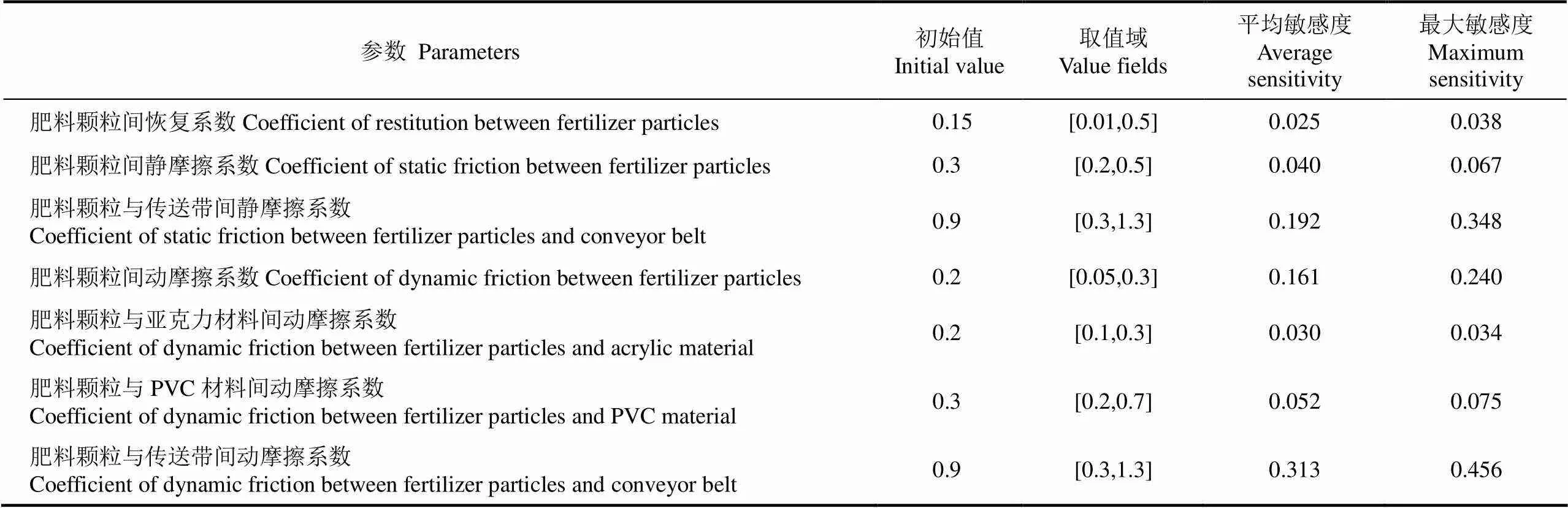
表1 配比变量排肥离散元模型参数初值、取值域及敏感度值

2.2 参数敏感度分析

2.2.1 分析方法

为了降低标定难度，需减少待标定参数数量，首先进行参数的敏感度分析，确定对肥料掺混均匀度影响较大的主因参数，只对主因参数进行标定。

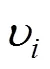
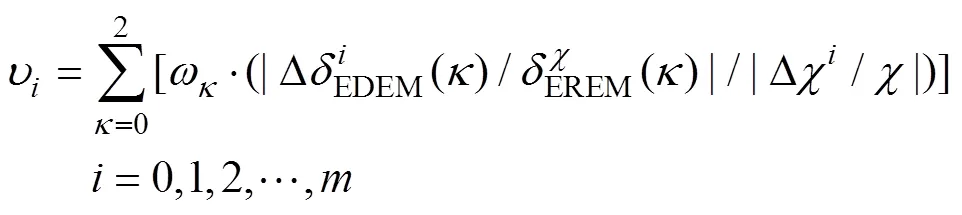
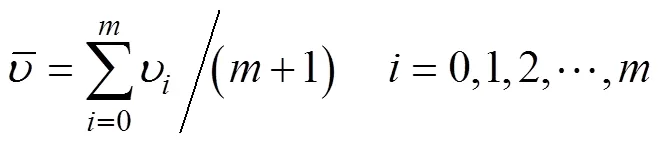
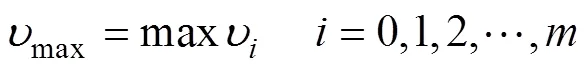
式中为该参数在经验取值域内的任意一个取值的代号；为肥料种类：0代表氮肥，1代表磷肥，2代表钾肥；为该参数的初始值；Δχ为该参数在其经验取值域内的任意一个取值相对于初始值的变化量；ΔδEDEM()为该参数经验取值域内的任意一个取值对应的某种肥料的掺混均匀度值相对于该参数取初始值时对应的同种肥料的掺混均匀度的变化量，δEDEM()为该参数取初始值时对应的某种肥料的掺混均匀度；ω为各种肥料的权重系数。

2.2.2 敏感度分析结果

2.3 掺混均匀度回归模型

标定的目的是建立精准的离散元模型，使配比变量排肥模型与真实排肥器在相同设计、作业参数下具有相同的肥料颗粒流动特征，所以设计、作业参数在标定过程中应为常量；进一步讲标定就是寻找最优模型参数值，保证仿真与试验排肥结果的表征参数值匹配一致。配比变量排肥结果的表征参数为肥料掺混均匀度以及排肥量，仿真中发现改变模型参数值后仿真排肥量与同工况下试验排肥量的相对误差均小于3%，说明排肥量受参数值的影响很小，而仿真排肥后的肥料掺混均匀度受模型参数值的影响很大，所以本文只将掺混均匀度作为配比变量排肥结果的表征。

为了获得最优参数值实现模型标定，需首先建立模型参数与掺混均匀度的映射关系。并且由上文参数敏感度分析可知，选定的3个主因参数对掺混均匀度影响最大，所以本文将主因参数作为输入量，将肥料掺混均匀度作为输出量，采用相关向量机以及二次多项式构建肥料掺混均匀度回归函数。

在选定的3个主因参数取值域内，采用MATLAB/ FieldD函数随机抽样，生成72个输入端训练样本以及24个输入端测试样本，以输入端测试样本中的个体作为离散元模型主因参数值，其他非主因参数值仍根据经验设为初始值，进行72组仿真，工况参数同试验一致，将3种肥料的掺混均匀度值的集合，分别作为该种肥料掺混均匀度回归模型输出端训练样本，采用相同方法生成回归模型输出端测试样本。

2.3.1 RVM回归模型

采用RVM训练3种肥料的掺混均匀度回归模型，训练结果如图2所示。采用生成的输入端测试样本，对训练后的模型进行测试，结果如图3所示。

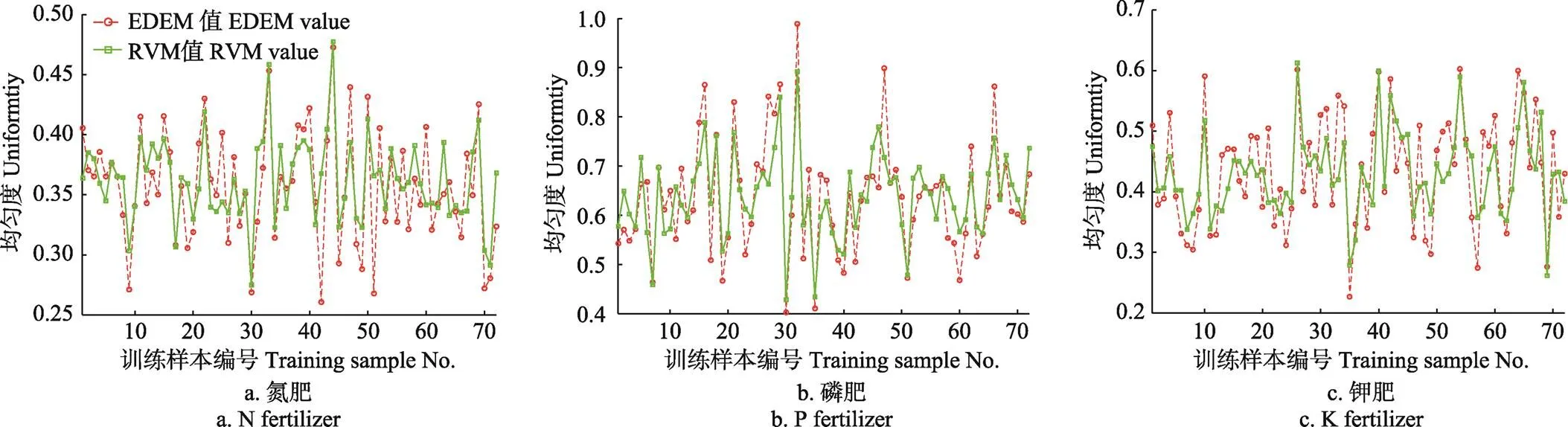
注：训练样本指在主因参数取值域内随机生成的作为离散元模型参数值的输入样本以及采用输入样本仿真生成的作为输出样本的肥料掺混均匀度值。

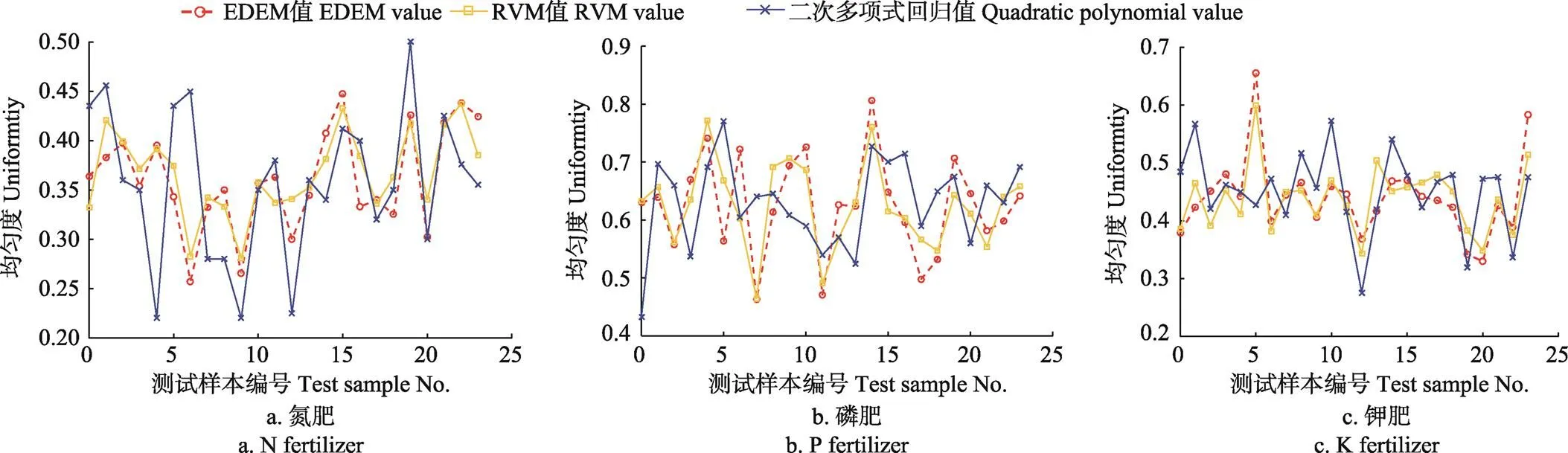
图3 不同肥料掺混均匀度模型测试结果

2.3.2 二次多项式回归模型

使用上述RVM回归模型的训练样本，建立上述3个主因参数与氮磷钾3种肥料掺混均匀度之间的二次多项式回归模型

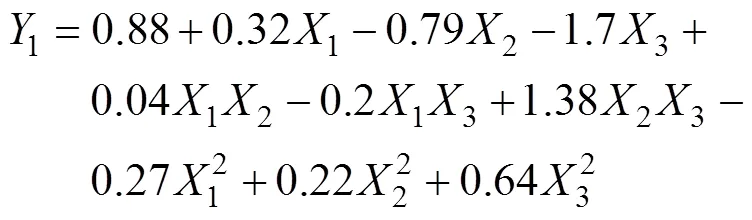
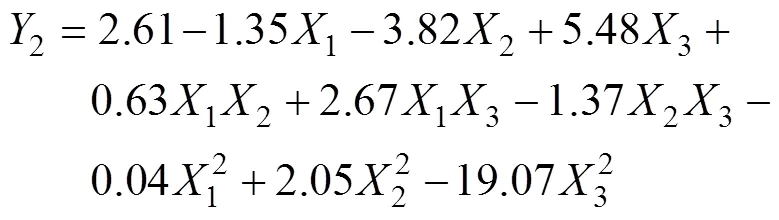
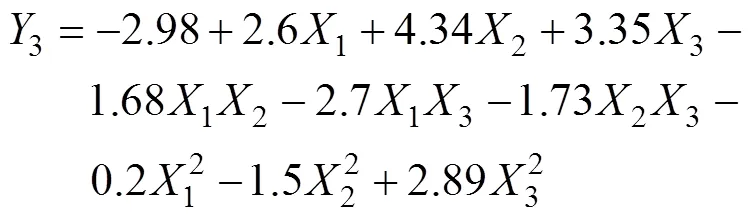
式中1、2、3分别为氮、磷、钾肥料的掺混均匀度，1、2、3分别为肥料与传输带之间的动摩擦系数、静摩擦系数以及肥料颗粒之间的动摩擦系数。采用上述生成的测试样本，对建立的3种肥料的二次多项式回归模型进行测试，结果如图3所示。

2.3.3 回归模型性能分析

比较RVM回归模型、二次多项式回归模型的预测值与EDEM模型仿真值的逼近程度，可以很直观地看出在相同的样本下采用RVM建立的肥料掺混均匀度回归模型预测效果较好。

为了定量分析回归模型性能，计算RVM回归模型以及二次多项式回归模型的预测平均相对误差（mean relative error, MRE）和决定系数（2），如图4所示，MRE和2采用如下公式计算：

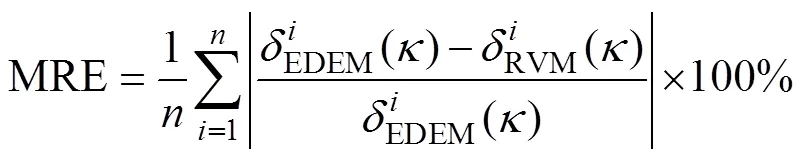
（13）

由图4分析可知，3种肥料掺混均匀度RVM回归模型决定系数为：氮肥0.887、磷肥0.819、钾肥0.849，平均相对误差为：氮肥5.43%、磷肥5.03%、钾肥6.43%；3种肥料掺混均匀度二次多项式回归模型决定系数为：氮肥0.363、磷肥0.123、钾肥0.260，平均相对误差为：氮肥16.35%、磷肥15.61%、钾肥14.64%。上述结果表明，由于配比变量排肥离散元模型非线性程度较高，二次多项式回归不能很好地表征主因参数和掺混均匀度之间的函数关系，RVM回归主因参数与掺混均匀度之间的函数关系是可行有效的，回归后的模型具有较高的精度。

2.4 基于遗传算法对主因参数最优值求解

2.4.1 数学模型

如何有效地获得最优主因参数值，使得标定后的离散元模型的排肥结果与试验值一致，并且实现主因参数标定的主动寻优，这是一个最优化问题。GA是解决最优化问题的有效方法，本文将一组主因参数看作一个染色体，在主因参数的经验取值域内，随机生成多组参数作为种群，主因参数适应度函数基于训练好的RVM回归模型构建，对应某一组主因参数，通过回归模型预测出的肥料掺混均匀度与试验值越接近，表明这一组主因参数越优良，考虑3种肥料的权重，主因参数适应度函数为

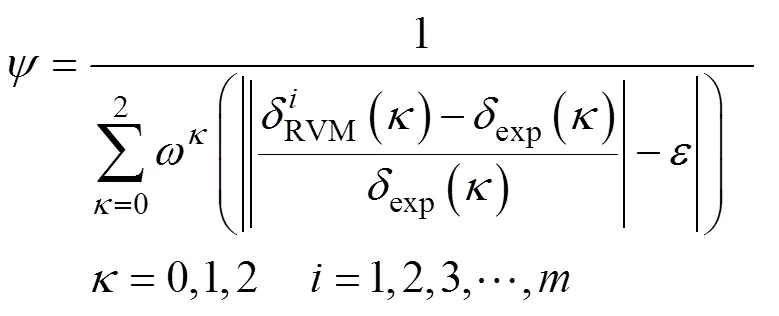
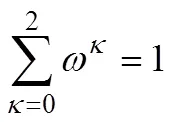
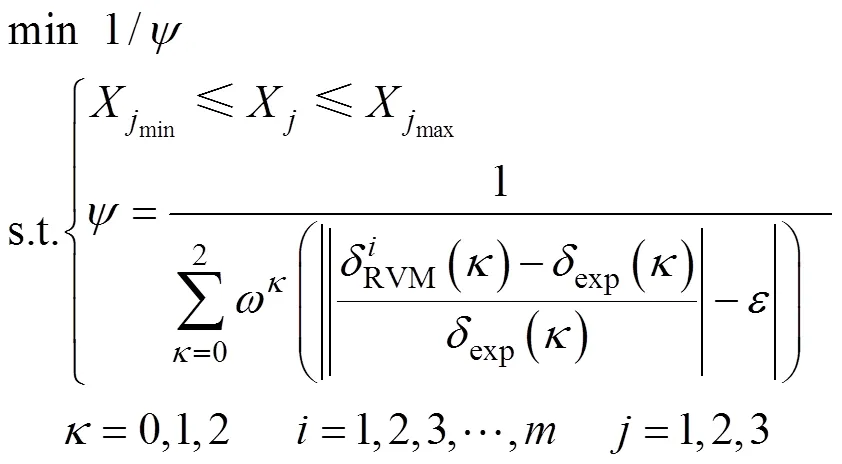
式中X为主因参数，Xmin为主因参数经验取值域下限，Xmax为主因参数经验取值域上限。

2.4.2 模型求解

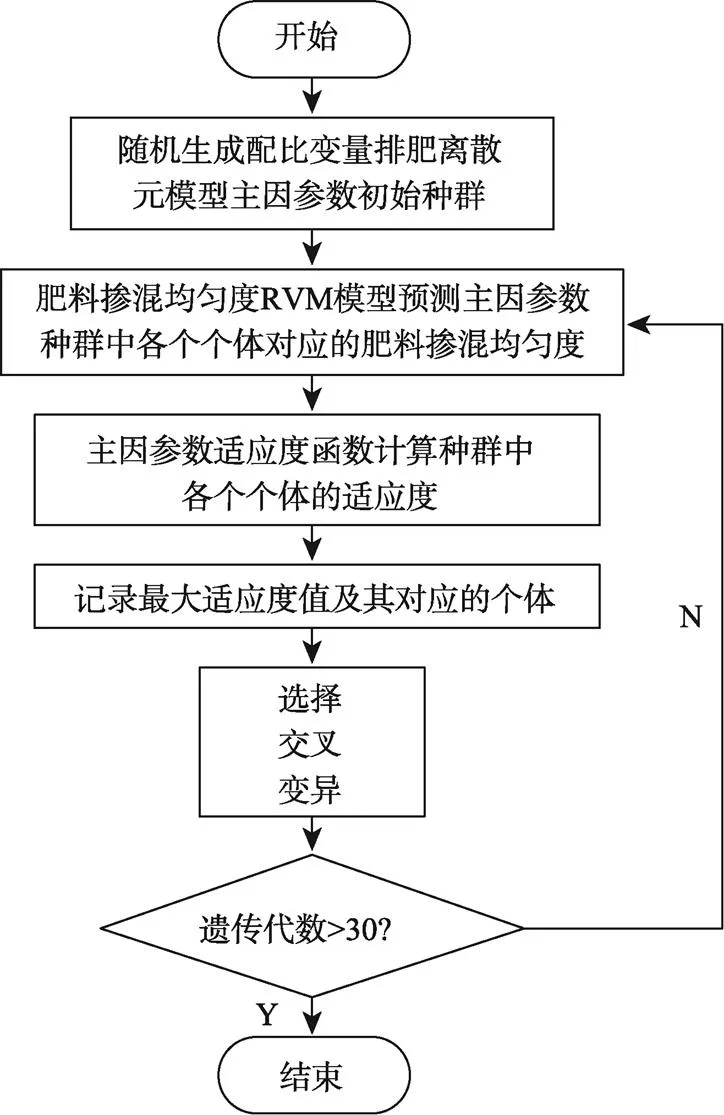
图5 最优主因参数值计算流程

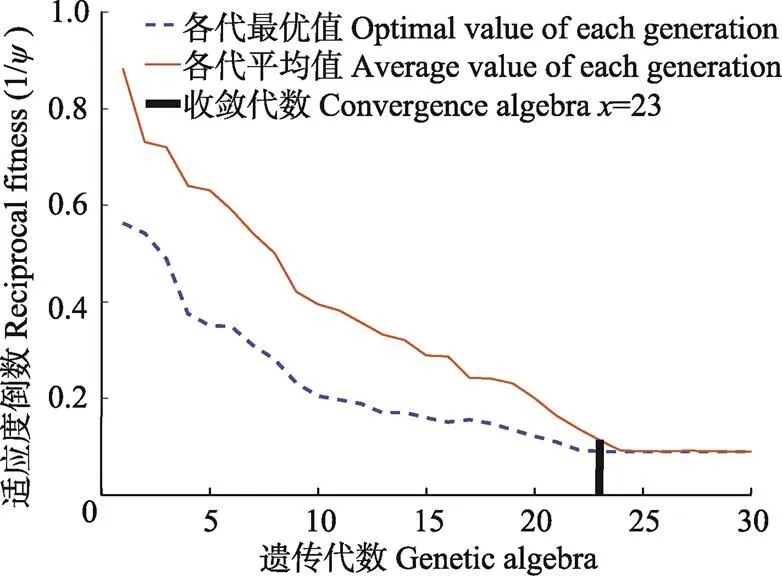
图6 遗传算法进化过程

3 标定参数排肥仿真应用及试验验证

为了验证标定方法及结果的正确性，进行了标定后的配比变量排肥离散元仿真与排肥试验，仿真与试验同工况，具体为：分别采用A型、B型、C型3种掺混腔（如图7），每一种掺混腔下，实施3个外槽轮排肥器转速相同，且分别为30、40、50、60、70 r/min的5组试验，每一组试验中排肥器肥舌开度均设置为最小；传送带的速度设定为0.6 m/s；3根落肥管居中一根的长度均为850 mm，内径为36 mm；排肥管为波纹管，轴向截面为三角形波浪纹，三角纹高度为2 mm，外径为45 mm，内径为42 mm，长度为480 mm。

将采用B型掺混腔的3种排肥转速下的仿真与试验结果进行比较，从图8中可以看出，相同排肥转速下，仿真与试验排肥后的中心肥带的带宽较为一致，且仿真排肥后的中心肥带很好地呈现出与试验相似的由于外槽轮脉动排肥造成的局部不均匀现象。试验排肥后有更多的肥料颗粒远离中心肥带，这可能是由于实际排肥过程中传送带的轻微振动，导致部分颗粒的流动性增强，产生了更显著的横向扩散现象。A型和C型掺混腔排肥后的肥带呈现出与B型掺混腔排肥带相似的特征。由仿真与试验结果的相似性，说明本文标定方法是有效可行的。

a. A型 a. A typeb. B型 b. B typec. C型 c. C type

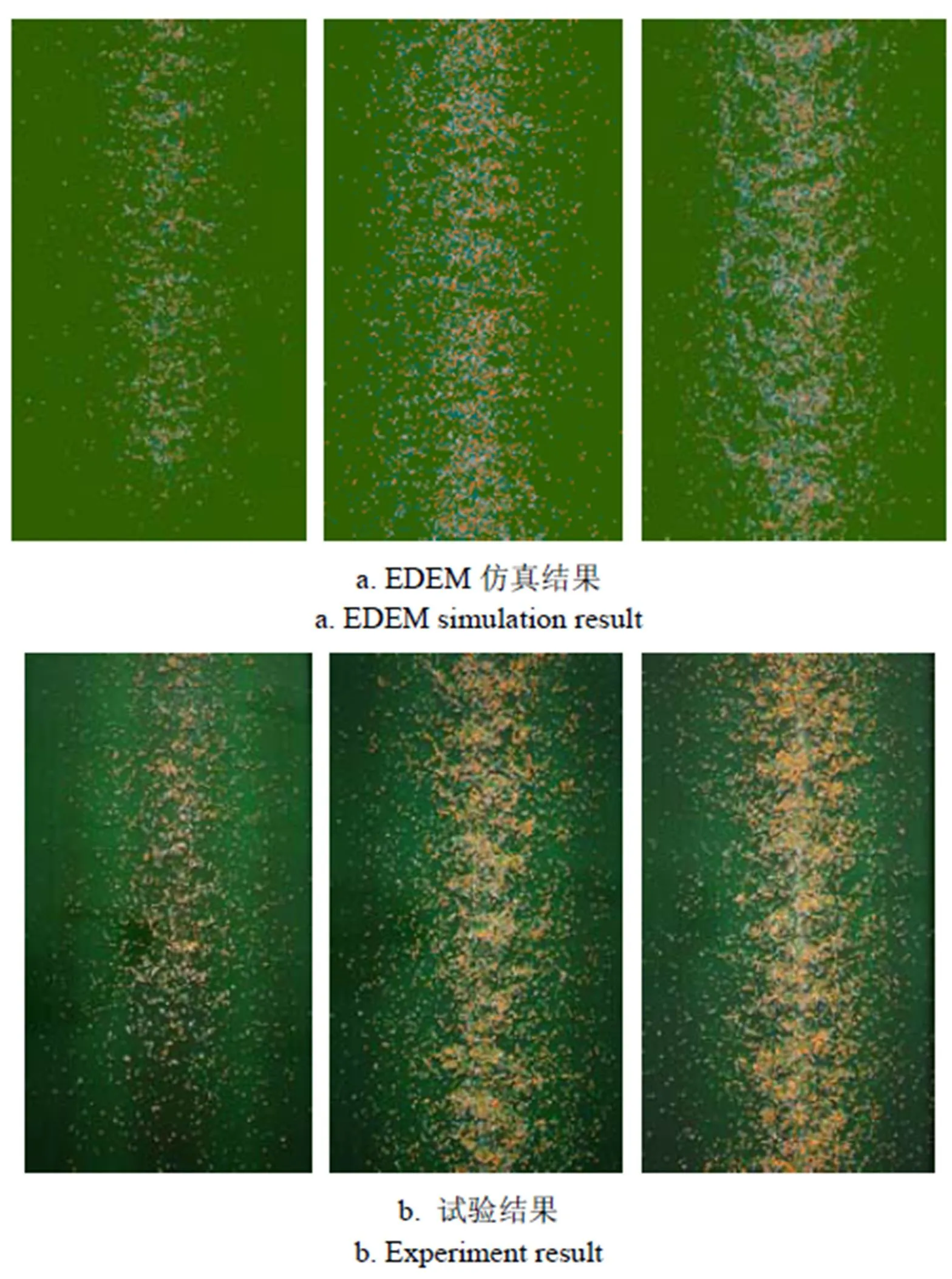
注：从左至右排肥转速依次为30、50、70 r∙min–1。

为了定量分析，同一排肥转速进行5次重复试验，取平均值，作为此排肥转速下的肥料掺混均匀度，仿真及试验排肥后的结果，如图9所示。

5种排肥转速下，排肥器采用碰撞边缘为外凸曲线形的A型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为6.4%，磷肥为4.1%，钾肥为5.9%，模型标定前氮肥为26.8%，磷肥为28.9%，钾肥为36.1%；采用碰撞边缘为直线形的B型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为5.8%，磷肥为5.6%，钾肥为4.9%，模型标定前氮肥为21.9%，磷肥为32.5%，钾肥为28.9%；采用碰撞边缘为内凹曲线形的C型掺混腔时，标定模型排肥后肥料掺混均匀度与试验值的相对误差均值：氮肥为5.0%，磷肥为3.7%，钾肥为8.7%，模型标定前氮肥为36.2%，磷肥为31.6%，钾肥为24.4%。表明该方法能够实现配比变量排肥离散元仿真参数准确有效的标定。

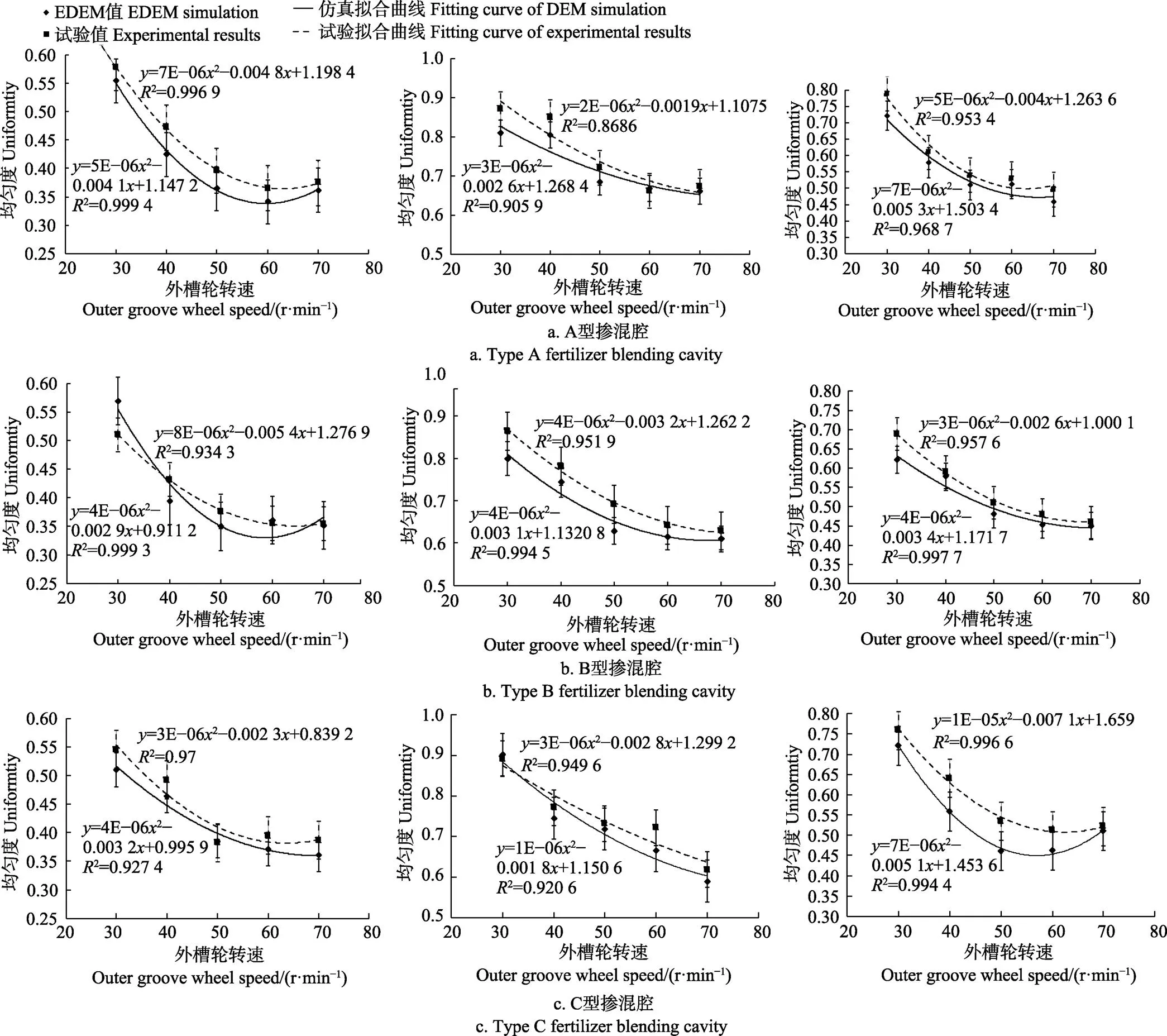
注：从左至右依次为N、P、K肥均匀度。

4 结 论

本文提出一种采用RVM构建肥料掺混均匀度与EDEM排肥模型参数回归函数，并通过GA算法求解最优参数值的配比变量排肥离散元模型参数标定方法。由参数敏感度分析可知，肥料与传输带之间的动摩擦系数及静摩擦系数、肥料颗粒之间的动摩擦系数对仿真排肥后的肥料掺混均匀度影响显著，为主要被标定参数；掺混均匀度对其余离散元模型参数（泊松比、剪切模量、恢复系数等）不敏感。

1）建立了配比变量排肥离散元模型参数与仿真排肥后肥料掺混均匀度的回归模型，3种肥料RVM回归模型的MRE和2值，氮肥为：5.43%、0.887，磷肥为：5.03%、0.819，钾肥为：6.43%、0.849；3种肥料二次多项式回归模型的MRE和2值，氮肥为：16.35%、0.363，磷肥为：15.61%、0.123，钾肥为：14.64%、0.260；结果表明RVM回归模型具有较高的预测精度。

2）依据RVM回归模型预测的肥料掺混均匀度值与试验值的偏离程度，构建了适应度函数，采用遗传算法迭代生成了主因参数最优值；试验结果表明，标定后模型较标定前模型排肥误差有大幅降低，说明了本文方法标定配比变量排肥离散元模型参数的正确性。

[1] Torbett J C, Roberts R K, Larson J A, et al. Perceived improvements in nitrogen fertilizer efficiency from cotton precision farming[J]. Computers and Electronics in Agriculture, 2008, 64(2): 140－148.

[2] 陈贤友，吴良欢，韩科峰，等. 包膜尿素和普通尿素不同掺混比例对水稻产量与氮肥利用率的影响[J]. 植物营养与肥料学报，2010，16(4)：918－923. Chen Xianyou, Wu Lianghuan, Hang Kefeng, et al. Effects of different mixture rates of coated urea and prilled urea on rice grain yield and nitrogen use efficiency[J]. Acta Metallurgica Sinica, 2010, 16(4): 918－923. (in Chinese with English abstract)

[3] 吴巍. 科学施肥技术[M]. 北京：科学出版社，1998．

[4] 何勇. 精细农业[M]. 杭州：浙江大学出版社，2003．

[5] 苑进，刘雪美. 肥量配比全变量施肥装置及其控制方法中国：CN102487644A [P].2012-06-13.

[6] 韩丹丹，张东兴，杨丽，等. 基于EDEM-CFD耦合的内充气吹式排种器优化与试验[J]. 农业机械学报，2017，48(11)：43－51. Han Dandan, Zhang Dongxing, Yang Li, et al. Optimization and experiment of inside-filling air-blowing seed metering device based on EDEM-CFD[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(11): 43－51. (in Chinese with English abstract)

[7] 韩丹丹，张东兴，杨丽，等. 内充气吹式玉米排种器工作性能EDEM-CFD模拟与试验[J]. 农业工程学报，2017，33(13)：23－31. Han Dandan, Zhang Dongxing, Yang Li, et al. EDEM-CFD simulation and experiment of working performance of inside-filling air-blowing seed metering device in maize[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(13): 23－31. (in Chinese with English abstract)

[8] 朱德泉，李兰兰，文世昌，等. 滑片型孔轮式水稻精量排种器排种性能数值模拟与试验[J]. 农业工程学报，2018，34(21)：17－26. Zhu Dequan, Li Lanlan, Wen Shichang, et al. Numerical simulation and experiment on seeding performance of slide hole-wheel precision seed-metering device for rice[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(21): 17－26. (in Chinese with English abstract)

[9] 廖庆喜，张朋玲，廖宜涛，等．基于EDEM的离心式排种器排种性能数值模拟[J]. 农业机械学报，2014，45(2)：109－114. Liao Qingxi, Zhang Pengling, Liao Yitao, et al. Numerical simulation on seeding performance of centrifugal rape-seed metering device based on EDEM [J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(2): 109－114. (in Chinese with English abstract)

[10] 张涛，刘飞，赵满全，等．基于离散元的排种器排种室内玉米种群运动规律[J]. 农业工程学报，2016，32(22)：27－35. Zhang Tao, Liu Fei, Zhao Manquan, et al. Movement law of maize population in seed room of seed metering device based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(22): 27－35. (in Chinese with English abstract)

[11] Elvis López Bravo, Engelbert Tijskens, Miguel Herrera Suárez, et al. Prediction model for non-inversion soil tillage implemented on discrete element method[J]. Computers and Electronics in Agriculture, 2014, 106: 120－127.

[12] Salar M R, Esehaghbeygi A, Hemmat A. Soil loosening characteristics of a dual bent blade subsurface tillage implement[J]. Soil & Tillage Research, 2013, 134: 17－24.

[13] Korné l Tamás, István J Jóri, Abdul M Mouazen. Modelling soil–sweep interaction with discrete element method[J]. Soil & Tillage Research, 2013, 134: 223－231.

[14] Franck Bourrier, Franc ois Kneib, Bruno Chareyre, et al. Discrete modeling of granular soils reinforcement by plant roots[J]. Ecological Engineering, 2013, 61: 646－657.

[15] Leblicq Tom, Smeets Bart, Ramon Herman, et al. A discrete element approach for modelling the compression of crop stems[J]. Computers and Electronics in Agriculture, 2016, 123: 80－88.

[16] 苑进，刘勤华，刘雪美，等. 多肥料变比变量施肥过程模拟与排落肥结构优化[J]. 农业机械学报，2014，45(11)：81－87. Yuan Jin, Liu Qinhua, Liu Xuemei, et al. Simulation of multi-fertilizers blending process and optimization of blending cavity structure in nutrient proportion of variable rate fertilization[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(11): 81－87. (in Chinese with English abstract)

[17] 苑进，刘勤华，刘雪美，等. 配比变量施肥中多肥料掺混模拟与掺混腔结构优化[J]. 农业机械学报，2014，45(6)：125－132. Yuan Jin, Liu Qinhua, Liu Xuemei, et al. Granular multi- flows fertilization process simulation and tube structure optimization in nutrient proportion of variable rate fertilization[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(6): 125－132. (in Chinese with English abstract)

[18] 黄小毛，查显涛，潘海兵，等. 油菜籽粒点面接触碰撞中恢复系数的测定及分析[J]. 农业工程学报，2014，30(24)：22－29. Huang Xiaomao, Zha Xiantao, Pan Haibing, et al. Measurement and analysis of rapeseeds’ restitution coefficient in point-to-plate collision model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(24): 22－29. (in Chinese with English abstract)

[19] 韩燕龙. 碾米机内米粒运动特征及碾白特性[D]. 哈尔滨：东北农业大学，2017. Han Yanlong. Study on the Movement Characteristics and the Whitening Behavior of Rice Grains in a Friction Type Mill[D]. Harbin: Northeast Agricultural University, 2017. (in Chinese with English abstract)

[20] González-Montellano C, Fuentes J M, Ayuga-Téllez E, et al. Determination of the mechanical properties of maize grains and olives required for use in DEM simulations[J]. Journal of Food Engineering, 2012, 111(4): 553－562.

[21] 贾富国，韩燕龙，刘扬，等. 稻谷颗粒物料堆积角模拟预测方法[J]. 农业工程学报, 2014, 30(11)：254－260. Jia Fuguo, Han Yanlong, Liu Yang, et al. Simulation prediction method of repose angle for rice particle materials[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(11): 254－260. (in Chinese with English abstract)

[22] Coetzee C J, Els D N J. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling[J]. Computers & Electronics in Agriculture, 2009, 65(2): 198－212.

[23] Ucgul M, Fielke J M, Sarnders C. Three-dimensional discrete element modeling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil[J]. Biosystems Engineering, 2014, 121(2): 105－117.

[24] 王云霞，梁志杰，张东兴，等. 基于离散元的玉米种子颗粒模型种间接触参数标定[J]. 农业工程学报, 2016, 32(22)：36－42. Wang Yunxia, Liang Zhijie, Zhang Dongxing, et al. Calibration method of contact characteristic parameters for corn seeds based on EDEM[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(22): 36－42. (in Chinese with English abstract)

[25] 刘凡一，张舰，李博，等. 基于堆积试验的小麦离散元参数分析及标定[J]. 农业工程学报, 2016, 32(12)：247－253. Liu Fanyi, Zhang Jian, Li Bo, et al. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 247－253. (in Chinese with English abstract)

[26] 苑进，刘成良，古玉雪，等. 基于相关向量机的双变量施肥控制序列优化[J]. 农业机械学报, 2011, 42(增刊1)：184－189，171. Yuan Jin, Liu Chengliang, Gu Yuxue, et al. Bivariate fertilization control sequence optimization based on relevance vector machine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 41(Supp.1): 184－189,171. (in Chinese with English abstract)

[27] 苑进. 贝叶斯学习框架下非线性制造过程建模及多目标优化关键技术研究[D]. 上海：上海大学，2008. Yuan Jin. Research on Some Key Issues of Bayesian Learning Framework Based Nonlinear Manufacturing Process Modeling and Multiobjective Optimization[D]. Shanghai: Shanghai University, 2008. (in Chinese with English abstract)

[28] Liu Xuemei, Zhang Xiaohui, Yuan Jin. Relevance vector machine and fuzzy system based multi-objective dynamic design optimization: A case study[J]. Expert Systems with Applications, 2010, 37: 3598－3604.

[29] 刘雪美，张晓辉，刘丰乐，等. 喷杆喷雾机风助风筒相关向量机多目标优化设计[J]. 农业机械学报，2010，41(6)：75－80. Liu Xuemei, Zhang Xiaohui, Liu Fengle, et al. Multi- objective dynamic design optimization for air duct of air-assisted boom sprayer based on RVM[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(6): 75－80. (in Chinese with English abstract)

[30] Yuan J, Wang K S, Yu T, et al. Integrating relevance vector machines and genetic algorithms for optimization of seed-separating process[J]. Engineering Applications of Artificial Intelligence, 2007, 20(7): 970－979.

[31] Coetzee C J, Lombard S G. Discrete element method modelling of a centrifugal fertilizer spreader[J]. Biosystems Engineering, 2011, 109(4): 308－325.

[32] Ding Shangpeng, Bai Lu, Yao Yuxiang, et al. Discrete element modelling (DEM) of fertilizer dual-banding with adjustable rates[J]. Computers and Electronics in Agriculture, 2018, 152: 32－39.

[33] Holland J. Searching nonlinear functions for high values[J]. Applied Mathematics and Computation, 1989, 32(23): 255－274.

Discrete element model simulation and verification of fertilizer blending uniformity of variable rate fertilization based on relevance vector machine

Yuan Jin, Xin Zhenbo, Niu Ziru※, Li Yang, Liu Xinghua, Xin Shuai, Wang Jianfu, Wang Liheng

(271018,)

With the development of computer simulation technology, the model establishment of variable rate fertilization with EDEM, demonstrates effectively the microcosmic dynamics behavior of fertilizer particles which can’t be analyzed by experiments. The calibration of discrete element model parameters mainly includes experimental determination and indirect calibration. When method of particle board is used to measure the static friction coefficient between particles, particle bounce and collision are inevitable and accuracy is difficult to pursue. The method of indirect calibration, using try-and-error method or quadratic polynomial regression, isn’t appropriate for the discrete element model of variable rate fertilization with nonlinear as well as multiple parameter values to be calibrated. Aiming at the problem above, a calibration method based on relevance vector machine is proposed. The discrete element simulation process of variable rate fertilization is a nonlinear system regarding model parameters as input and uniformity of fertilizer blending as output (when a group of parameters are given, certain uniformity value of fertilizer blending can be gotten by fertilization simulation). Firstly, the model parameter influencing the fertilization outcome of the discrete element simulation most can be defined as the main parameters by sensitivity analysis. The value domain of each main parameters are found and then the sample of parameters are got. The sample of parameters and the corresponding uniformity of fertilizer blending are regarded as training and test sample. The relevance vector machine is used to reveal mapping relationship between model parameters and the uniformity, and the regression model is established. The uniformity based on the optimal model parameters should be consistent with the that in experiment, the model parameters fitness function is constructed combined the established models with experimental statistical results. Based on the mathematical thought of the constraint optimization, the mathematical model of optimal parameters calculating is established, and the optimal parameters are generated by the genetic algorithm. For A-type mixing cavity whose the collision edge is the outer convex curve, the mean relative error of uniformity between test values and simulation values from model calibrated: for nitrogen fertilizer is 6.4%, phosphate fertilizer of 4.1%, and potash fertilizer of 5.9%. While nitrogen fertilizer is 26.8%, phosphate fertilizer is 28.9% and potash fertilizer is 36.1% for the model before calibration. For B-type mixing cavity whose the collision edge is the straight-line, the mean relative error of uniformity from model calibrated: nitrogen fertilizer is 5.8%, phosphate fertilizer of 5.6% and potash fertilizer of 4.9%. While nitrogen fertilizer is 21.9%, phosphate fertilizer is 32.5% and potash fertilizer is 28.9% for the model before calibration. For C-type mixing cavity whose the collision edge is the concave curve, the mean relative error of uniformity from model calibrated: for nitrogen fertilizer is 5.0%, phosphate fertilizer of 3.7%, potash fertilizer of 8.7%. While nitrogen fertilizer is 36.2%, phosphate fertilizer is 31.6% and potash fertilizer is 24.4% for the model before calibration. The above results show that the method can be used to realize accurate calibration of discrete element model parameters of variable rate fertilization.

fertilizers; calibration; discrete element method; variable rate fertilization; relevance vector machine; genetic algorithm

2018-09-03

2019-02-24

山东省重点研发计划项目（2018GNC112017）；国家重点研发计划资助（2017YFD0701103-3）；国家自然科学基金资助项目（51475278、51675317）；山东省“双一流”奖补资金资助（SYL2017XTTD14）

苑 进，教授，博士，主要从事智能农机装备相关研究。 Email：jyuan@sdau.edu.cn

牛子孺，副教授，博士，主要从事智能农机装备、数字设计与制造相关研究。Email：cherokeesaab@163.com

10.11975/j.issn.1002-6819.2019.08.005

S220.1

A

1002-6819(2019)-08-0037-09

苑 进，辛振波，牛子孺，李 扬，刘兴华，辛 帅，王建福，汪力衡.基于RVM的配比变量排肥掺混均匀度离散元仿真及验证[J]. 农业工程学报，2019，35(8)：37－45. doi：10.11975/j.issn.1002-6819.2019.08.005 http://www.tcsae.org

Yuan Jin, Xin Zhenbo, Niu Ziru,Li Yang, Liu Xinghua, Xin Shuai, Wang Jianfu, Wang Liheng.Discrete element model simulation and verification of fertilizer blending uniformity of variable rate fertilization based on relevance vector machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(8): 37－45. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.08.005 http://www.tcsae.org