冷连轧过程中间辊弯辊力设定策略研究

谷 田 ，王海涛 ，冯运莉，周国平 ，刘春雨

（1.唐山钢铁集团有限责任公司，河北 唐山 063000；2.华北理工大学，河北 唐山 063210）

冷轧带钢尺寸精度高，表面质量好，机械、工艺性能优越，被广泛的应用于国民经济的各个领域，其中板形是衡量冷轧带钢质量的重要指标。针对冷连轧过程的板形控制，国内外众多学者都进行了深入的研究。陈金山等[1]分析了最佳弯辊力对成品带钢板形的影响规律，并建立了最佳弯辊力计算模型。Wang等[2]提出了一种冷连轧穿带过程的动态模型，模拟计算结果表明，提出的模型与实际值吻合较好，提高了板形控制精度。

学者们对板形执行机构与带钢轧后板形的关系进行了深入研究，但是均忽略了中间辊弯辊的重要性。本文基于影响函数法，分析了中间辊弯辊与中间辊横移位置对板形的影响规律，提出了冷连轧过程中间辊弯辊设定策略。

1 冷轧带钢板形预测模型建模

1.1 轧辊弹性变形模型

承载辊缝的形状直接决定带钢轧后断面分布，因此轧辊弹性变形模型在板形控制理论中的地位相当重要。使用影响函数法计算了辊系弹性变形，带钢轧后厚度分布如下：

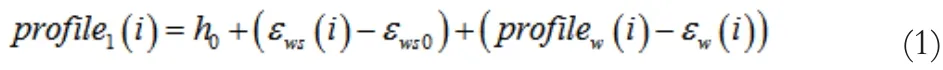
1.2 轧后带钢残余应力计算模型

根据胡克定律，带钢轧后残余应力分布可按式(2)计算得到：

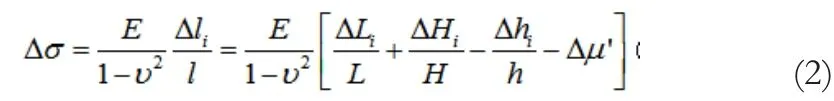
式中：为轧后带钢残余应力；为带钢弹性模量；为带钢泊松比。

2 中间辊弯辊力设定策略研究

2.1 中间辊弯辊力对轧后带钢断面分布和板形的影响

为了研究中间辊弯辊力对轧后带钢断面分布和板形的影响，基于某厂冷连轧机的参数进行模拟计算。弯辊力分别选择300，400，500kN。当计算工作辊弯辊力时，中间辊弯辊力为400kN不变。当计算中间辊弯辊力时，工作辊弯辊力设为400kN不变。

工作辊弯辊力(WRB)对带钢断面分布的影响如图1(a)所示。工作辊弯辊力由300kN升至500kN，轧后带钢由正凸度向负凸度过渡。图1(b)为不同工作辊弯辊力下轧后带钢板形。可以看出，工作辊弯辊力由300kN升至500kN，轧后带钢由中浪向边浪过渡。图1(c)为不同中间辊弯辊力(IRB)下轧后带钢断面分布，随着中间辊弯辊力的上升，带钢凸度逐渐减小。图1(d)为不同中间辊弯辊力下轧后带钢的板形。可以看出，中间辊弯辊力为300kN时，带钢呈现轻微1/4浪，随着中间辊弯辊力的增加，1/4浪逐渐向中浪转变。中间辊弯辊力对带钢断面分布的影响在带钢边部至距边部1/4处较大，而工作辊弯辊力可以影响至带钢中部。

图1 工作辊弯辊力对(a)带钢断面分布，(b)板形的影响；中间辊弯辊力对(c)带钢断面分布，(d)板形的影响

2.2 中间辊横移对中间辊弯辊板形调控能力的影响

六辊轧机的中间辊横移位置由轧制带钢的宽度决定，为了消除工作辊的有害弯矩，中间辊一端会横移至距离带钢边部δmm的位置。计算了不同δ值下的轧后带钢板形及凸度。δ分别为0，50，100mm，每个δ下分别选择300，400，500kN三种中间辊弯辊力进行模拟计算[3-5]，计算结果如图2所示。

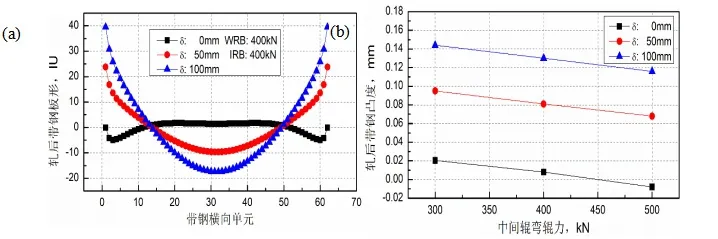
图2 (a)δ对轧后带钢板形的影响；(b)δ对轧后带钢凸度的影响

图2 (a)为工作辊、中间辊弯辊力均为400kN时，中间辊横移位置δ对轧后板形的影响。随着δ的增加，中间辊端部与带钢的距离增加，由于轧制力引起的轧辊挠曲增加，轧后带钢板形由良好向边浪缺陷转变。图2(b)为不同δ下，中间辊弯辊力的变化对轧后带钢凸度的影响。可以看出，随着中间辊弯辊力的增加，带钢凸度降低，δ越高，带钢凸度越大，这也是由于轧辊挠曲的增大而引起的。

2.3 中间辊弯辊力设定策略

综上所述，中间辊弯辊力对板形的调控能力虽然较弱，但由图1可知，中间辊弯辊对带钢断面1/4处的影响较工作辊弯辊明显，中间辊弯辊可用于对较小四次浪形的调控。由图2可以看出，增加中间辊横移位置δ可用于控制板形中浪缺陷。

中间辊弯辊对板形的调控能力远小于工作辊弯辊，所以在板形控制系统的设定计算中，调控能力弱的应该先计算，保证板形控制计算效率，所以中间辊弯辊的设定计算优先级应高于工作辊弯辊。而在板形控制系统的反馈控制中，与设定计算的顺序相反，调控能力强的应该先进行调节，保证板形缺陷能够迅速消除，所以中间辊弯辊的反馈控制调节优先级应低于工作辊弯辊。

3 现场应用及效果

将本文提出的中间辊弯辊设定策略应用在某冷连轧机组中。将反馈控制调节优先级设定为中间辊弯辊低于工作辊弯辊，并将S2机架中间辊弯辊力由340kN改为550kN，将S3机架中间辊弯辊力由370kN改为550kN，将S4机架中间辊弯辊力由420kN改为650kN。从应用效果来看，成品板形由11IU降至5IU以内，优化效果明显。

4 结论

①增加中间辊弯辊力，提升了工作辊弯辊的调控能力，可缓解带钢1/4浪板形缺陷；②中间辊横移位置δ增加，带钢凸度显著增加。随着δ的升高，带钢板形由中浪向边浪过渡；③将得到的控制策略应用于现场，板形质量显著提升；④采用影响函数法建立了六辊冷轧机辊系弹性变形计算模型，用于分析各种主要因素对最佳变辊力的影响规律；⑤建立了很多因素影响的工作辊弯辊力非线性回归模型，根据轧机的特性建立了基于工作辊弯辊力的中间辊弯辊力设定模型，从而简化了模型形式，降低了现场模型的调试和维护难度；⑥弯辊力设定值与实测值在20%以外的仅占总数的5.25%，这表明模型具有较高的设定精度[6]。