基于深部软弱煤岩条件下巷道蠕变规律的数值模拟分析

陈前款，吴德义

(安徽建筑大学，安徽 合肥 230022)

中国是世界上最大的发展中国家，特别是近几十年的快速发展，每年对资源的需求量都在快速增长。我国煤炭资源丰富，一直都是我国使用的主要能源，在全国大部分地区都有分布。但是，在已知的煤矿中，大约有一半的煤炭资源分布在地面以下一千多米的深度。而且由于我国煤炭资源分布广泛，地下深部岩石环境复杂等原因使得深部开采受到很多的制约因素。另外，我国东部煤矿的浅部煤炭资源已逐渐衰竭，从长远考虑，为了实现煤炭工业的可持续发展，深部开采已成为煤炭工业必须攻克的重大课题[1]。在深部煤矿开采过程中，大部分巷道布置在软弱煤层中。由于开挖后巷道周围岩石环境的改变，导致巷道表面的应力应变产生改变，超过一定的限值后就会产生巷道的蠕变变形破坏。大量的现场测量和室内试验表明:煤岩的蠕变属性更为显著[2]。目前巷道变形破坏成为我国深部开采的重要制约因素，严重影响巷道安全使用，保持围岩变形稳定已成为深部煤炭可持续安全高效开采的关键[3]。

数值模拟技术作为岩石力学研究的一种新的方法和手段，已经在诸如大尺度岩石力学试验模拟以及岩石工程的力学行为仿真中得到了广泛运用[4]。在地底深部软弱煤岩条件下，本文利用FLAC 3D数值模拟软件并采用控制变量法对不同环境下(不同巷道尺寸、原岩应力和围岩黏聚力)巷道围岩水平和竖直方向的蠕变特征进行模拟分析，从而总结分析出巷道围岩蠕变规律。

1 数值分析模型的建立

在深部软弱煤岩条件下，当围岩的应力场达到煤岩强度极限时，围岩就会产生蠕变[5]。巷道实际的蠕变规律是多种影响因素共同作用下的结果，在实际分析中不可能也没有必要将所有影响因素全部考虑在内。在本文中，简化的数值分析模型(图1)是综合矿上工程实际以及相关的理论知识，总结出主要的影响因素后建立起来的。

图1 数值分析模型

在图1的模型中，以矩形作为巷道的断面形式，并以矩形中心点作为原点建立模型。整个模型尺寸为60 m×2 m×60 m，计算范围内的网格划分从里向外的渐变比例设定为1.1，共有12544个计算单元。模型上边界设定受到原岩应力，其余边界受到相应方向的刚性约束。由于巷道开挖后周围原岩性质的改变，选用粘塑性(cvisc)蠕变本构模型能得到更好的模拟效果[6]。

2 数值分析计算

采用控制变量法分别分析不同巷道尺寸、原岩应力和围岩黏聚力下巷道各个方向的蠕变位移值，根据软件模拟出来的不同条件下的结果，研究水平和竖直方向的位移随时间变化的关系，通过总结分析得出规律性的结论。

2.1 不同巷道尺寸下蠕变位移变化规律

保持原岩应力为20 MPa和围岩黏聚力为1.5 MPa不变，并以120 d作为蠕变的发展时限。选取巷道尺寸分别为3 m×3 m、5 m×3 m、6 m×5 m得出的水平和数值方向的位移图如图2、图3、图4所示。

由于直接分析以上图形中蠕变位移随时间变化规律不够方便，利用Origin分析软件来分析以上数据得出图形如图5、图6所示。

图2 3 m×3 m下巷道表面位移图

巷道水平方向蠕变位移随时间变化曲线如图5所示，从图中可以看出在初始蠕变时期(蠕变前10 d内)三种巷道尺寸下的水平位移均发展较慢，且没有明显的差别；在10 d至25 d期间发展速度较快，但巷道尺寸对此阶段蠕变位移的影响较小，三条曲线接近重合；25 d之后巷道尺寸的对位移的影响开始明显地表现出来，三条曲线出现较大的区别，位移逐渐增大但蠕变位移发展速度逐渐降低直至位移趋于稳定。

巷道竖直方向蠕变位移随时间变化曲线如图6所示，与水平位移类似，在初始蠕变时期(蠕变前10 d内)三种巷道尺寸下的竖直位移均发展相对缓慢，且没有明显的差别；蠕变时间到10 d后位移发展速度相对前10 d较快，且与水平位移不同的是此时由于巷道尺寸的不同影响三条曲线开始出现分离；25 d之后位移逐渐增大但蠕变位移发展速度逐渐降低直至位移趋于稳定。

图3 5 m×3 m下巷道表面位移图

图4 6 m×5 m下巷道表面位移图

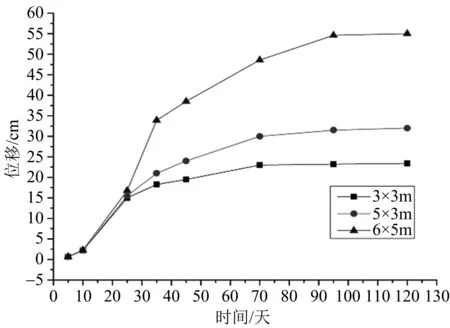
图5 巷道水平位移变化曲线

综合水平和竖直方向的位移变化特征可以看出，在蠕变前期蠕变量都比较小，且巷道尺寸对蠕变量的影响不大，在蠕变中前期之后巷道尺寸对位移的影响逐渐明显。同一时间点尺寸较大的巷道相对尺寸较小的巷道其蠕变位移和蠕变速度都较大，且较大巷道尺寸下的蠕变稳定时间也较长。相比竖向位移，同一时间点的水平位移也都比竖向位移大了许多，说明巷道帮部的蠕变要比顶板的更明显[7]。所以在深部软弱煤岩中，大尺寸巷道的蠕变现象较为显著，其导致的蠕变破坏风险比小尺寸巷道下的高很多，且帮部产生的破坏一般多于顶板。

2.2 不同原岩应力下蠕变位移变化规律

保持巷道尺寸为3 m×3 m，围岩黏聚力为1.5 MPa不变，并以120 d作为蠕变的发展时限。选取原岩应力分别为14 MPa、16 MPa、20 MPa得出的水平和竖直方向的位移图，运用 FLAC 3D 软件蠕变模块分析了不同应力条件下，无支护巷道的蠕变特性[8]。直接给出处理后的水平和竖直方向的位移与时间关系曲线如图7、8。

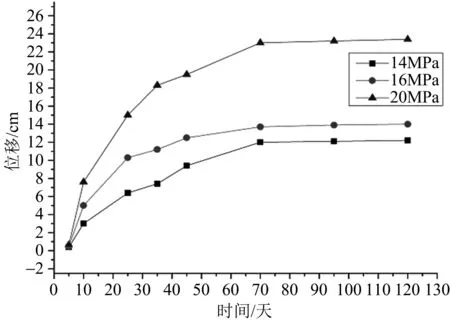
图7 巷道水平位移变化曲线

图6 巷道竖直位移变化曲线

不同原岩应力下巷道水平位移随时间变化关系如图7。蠕变前期位移发展速度最快，且一开始原岩应力的不同就对位移发展产生明显的影响，即应力越大，位移大小和发展速度都越大；10 d之后三条曲线分离明显且蠕变发展速度逐渐减小，直至70 d后蠕变位移逐渐稳定。

不同原岩应力下巷道竖直位移随时间变化关系如图8。蠕变前期位移发展速度也是最快的，且不同应力下竖直方向位移初始值就有了相对明显的区别，并且也表现出应力越大，位移大小和发展速度都越大的现象；10 d之后三条曲线分离明显且蠕变发展速度总体上是降低趋势，期间蠕变速度也会有短暂的回升；相对水平位移，竖向位移稳定时间较长，大概在一百天时趋于稳定。

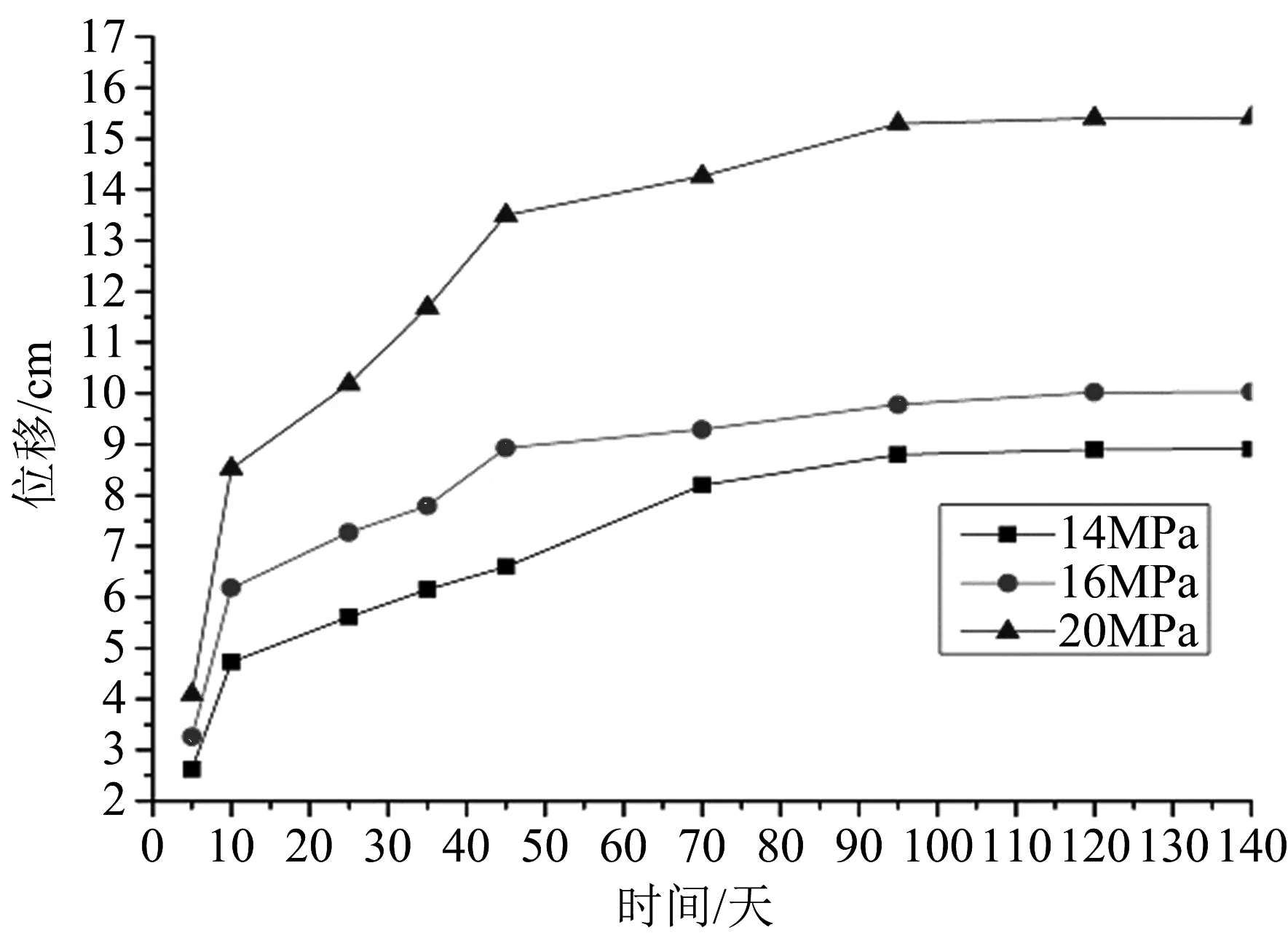
图8 巷道竖直位移变化曲线

综合比较不同原岩应力条件下水平和竖直方向的蠕变量随时间变化曲线，在蠕变整个过程中原岩应力对蠕变量的影响都比较大。同一时间点应力较大的巷道相对应力较小的巷道其蠕变位移和蠕变速度都较大，且较大应力下的蠕变稳定时间也较长。相比竖向位移，同一时间点的水平位移都比竖向位移大了许多，说明巷道帮部的蠕变要比顶板的更明显。在前70 d，蠕变速度变化较大，之后速度几乎没有变化，所以在深部软弱煤岩支护中，要重点做好前70d的检测和加固。深度越大的巷道其蠕变现象也越明显，其导致的蠕变破坏风险也很高。

2.3 不同围岩黏聚力下蠕变位移变化规律

保持巷道尺寸为3 m×3 m，原岩应力为20 MPa不变，并以120 d作为蠕变的发展时限。选取三种不同岩性其黏聚力分别为08 MPa、1.0 MPa、1.5 MPa得出的水平和竖直方向的位移图，直接给出处理后的水平和竖直方向的位移与时间关系曲线如图9、10。

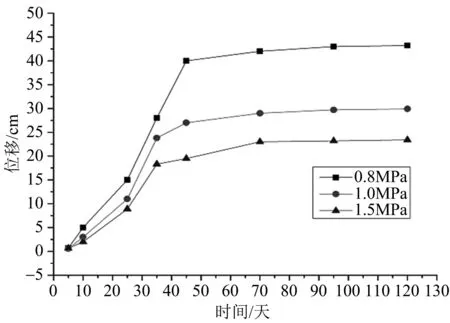
图9 巷道水平位移变化曲线

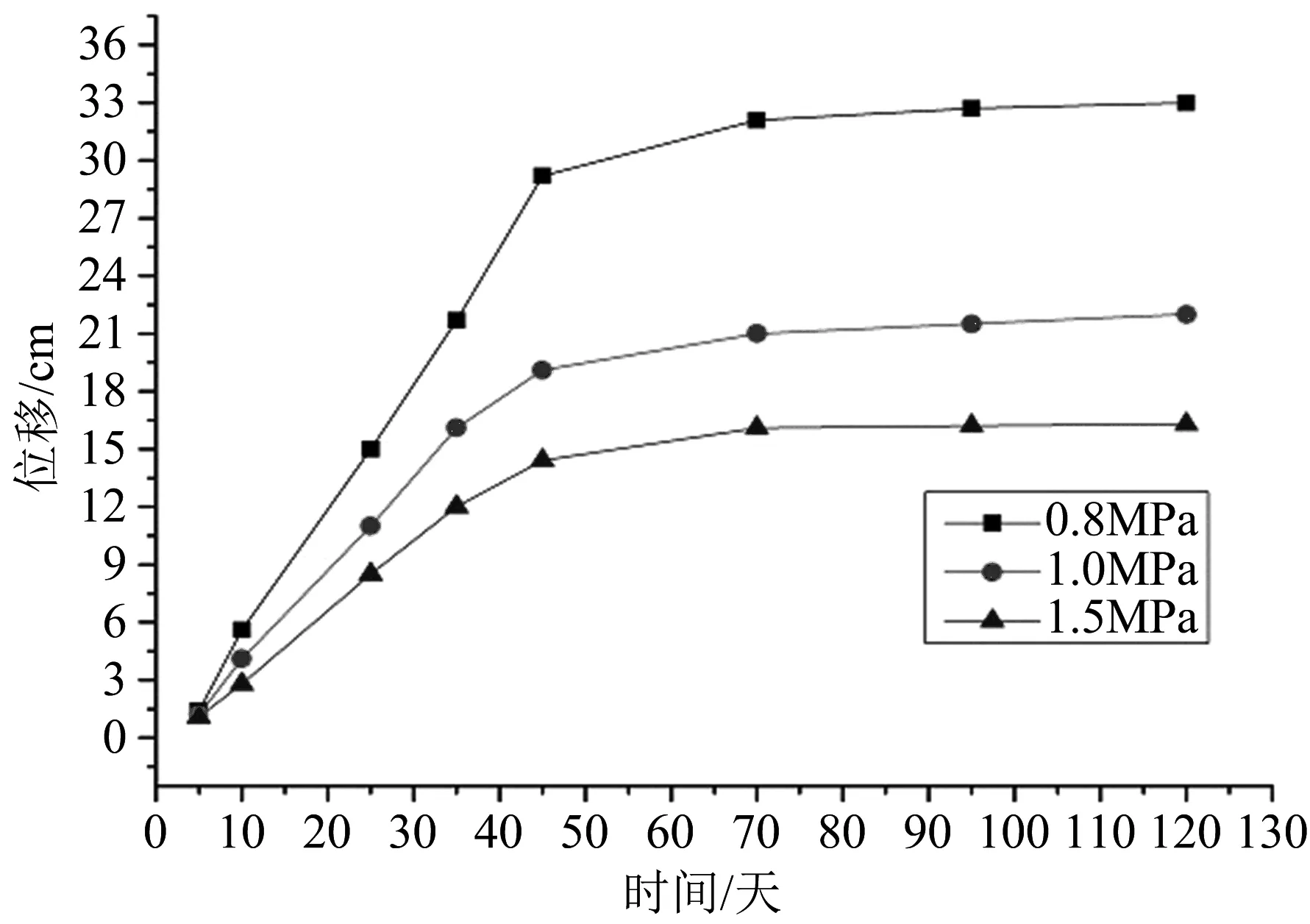
图10 巷道竖直位移变化曲线

从图9中可以看出，在不同围岩黏聚力下巷道水平方向的位移在起始阶段都比较小，三者位移值都相差不多。10 d至50 d之间巷道水平方向蠕变量快速增加，蠕变速度也快速增加到最大值；之后蠕变速度急剧下降，水平位移趋于稳定；随着围岩岩性的变差(即围岩黏聚力的减小)，蠕变量和蠕变速度逐渐增加，并且蠕变达到稳定的时间也相对增加。

图10显示，在不同围岩黏聚力下巷道舒适方向的位移在起始阶段也都比较小，三者位移值都相差不多，蠕变量在前50 d增加速度较快。但与水平方向不同的是，在前50 d内位移发展速度几乎保持不变并于45 d左右骤减直至围岩稳定。与水平方向相同，随着围岩岩性的变差(即围岩黏聚力的减小)，同一时间点蠕变量和蠕变速度都相对较大，并且蠕变达到稳定的时间也相对增加。

综合图9和10分析，在蠕变的起始阶段至稳定的全过程中围岩黏聚力对蠕变量、蠕变速度以及蠕变稳定时间的影响都比较大。无论是在水平还是竖直方向，同一时间点时岩性较差的巷道其蠕变位移和蠕变速度都较大，且蠕变稳定时间也较长。相比竖向位移，同一时间点的水平位移也都比竖向位移发展明显，说明巷道帮部的蠕变要比顶板的更明显。在前45 d，竖直方向蠕变速度没有明显变化，而水平方向速度变化较明显，之后两者速度几乎没有变化。深部软弱煤岩支护中，针对不同岩性的围岩前45 d的观测和支护尤为重要。

3 结语

(1)随着巷道尺寸、原岩应力增大以及围岩岩性的降低，巷道表面的蠕变位移发展程度大、速度快，且水平方向上的蠕变位移大于竖直方向的蠕变位移，趋于稳定的时间也增加。

(2)围岩的初始蠕变以及加速蠕变阶段一般在巷道开挖后70 d之内，故在工程实际中要加强前70 d的监测以及支护。

(3)当巷道尺寸发生变化，稳定时的蠕变量增加最多，增加幅度也较大。由此可见，在深部软弱煤岩中，巷道尺寸的大小对围岩表面蠕变量的影响较大。工程中应根据实际需要，在保证工程效率和需要等的条件下尽量选择较小的巷道尺寸。