基于AHP和排序比的高校本科教学质量评价方法

2019-05-24邓晓衡刘铁雄郑静益沈海澜

计算机教育 2019年5期

邓晓衡，刘铁雄,郑静益,沈海澜

（1.中南大学信息科学与工程学院，湖南长沙 410083；2.中南大学本科生院，湖南长沙 410083）

0 引言

教学质量是高等学校的生命线。教学质量评价是高等学校实现高校教学科学管理的重要保证。然而高校教学系统涉及主体多，影响因素多，具有开放性、复杂性等特征，给建立科学、有效的高校本科教学质量评价方法带来了难度。用哪些指标去评价，以及用什么样的方法去评价是教学质量评价的基本问题。学者针对教学质量评价从不同角度已经展开了许多有效的研究[1-4]。

1 总体方案

AHP层次分析法由美国著名的运筹学家、匹兹堡大学萨迪( T.L.Saaty) 教授提出[5]，其基本思想是通过对系统的多个因素的分析，划出各因素间相互联系的有序层次，并对每一层次的各因素给出相对重要性的定量表示，进而建立数学评价模型，计算出每一层次全部因素的相对重要性的权值。AHP层次模型主要包括目标层、中间层和方案层。

利用AHP层次方法研究本科教学质量评价问题的总体方案是：第一步，对专家通过座谈、问卷调查的方式确定本科教学质量评价指标，建立指标体系层次化框架；第二步，利用AHP方法，结合专家自身经验和专业知识，基于1-9标度法[6]分别对每一层内各项指标进行两两比较和重要性评价，建立判断矩阵；第三步，对判断矩阵进行一致性检验，计算得到每一层评价指标相对于上一层评价目标的量化权重；第四步，综合考虑指标的权重和被评目标的相对优势，建立综合考虑指标权重和相对排序的评价模型。

2 评价方法和过程

2.1 构建评价指标体系

在对专家进行问卷调查的基础上，依据AHP层次化模型，建立本科教学质量评价指标体系，见表1。其中包括一级指标6个（B1～B5），二级指标18个（C1～C18）和三级指标44个（D1～D44）。按照AHP模型，将本科教学质量G定义为目标层，一级指标、二级指标、三级指标分别定义为准则层1、准则层2和准则层3。

2.2 计算评价指标权重

根据AHP方法，首先采用1-9标度法分别对每一层内各项指标进行两两比较和重要性评价，建立判断矩阵。然后对判断矩阵进行一致性检验，计算该矩阵的最大特征值和其对应的特征向量。一致性检验通过，特征向量即为该层指标相对于上一层指标的权重；一致性检验没有通过，需要重新构造判断矩阵。以目标层G与准则层B的判断矩阵G-B表构造为例，见表2。

表1 高校本科教学质量评价指标体系层次框架

表2 目标层G与准则层1的判断矩阵G-B

计算该矩阵的最大特征值λmax和其对应的特征向量，得到λmax=6.11，特征向量w=（0.083 0.083 0.333 0.083 0.333 0.083）。

根据公式（1）和（2）以及平均随机一致性指标R.I.的取值[6]（表3）计算得到C.I.=0.000,C.R.= 0.000。

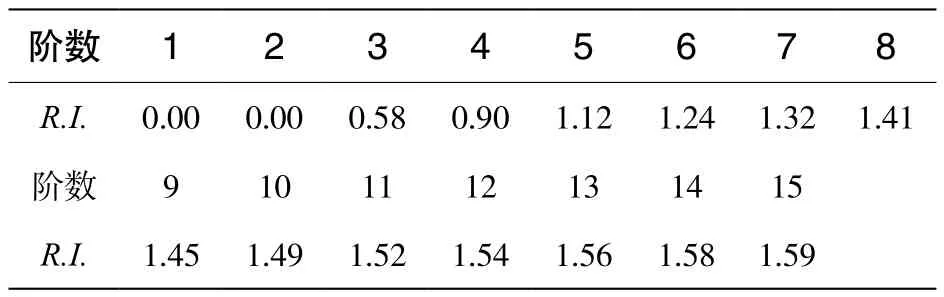
表3 平均随机一致性指标R.I.的取值

由于C.R.=0.000＜0.1表明判断矩阵具有可接受的一致性，所以最终优化后准则层1中各指标的权重为w=（0.083 0.083 0.333 0.083 0.333 0.083）按照上述方法依次计算出各层指标对其上一层指标的权重。各层指标相对于目标层G的权重则为该目标每一层的权重之积，如C1对B1的权重为0.333，B1对G的权重为0.083，则C1对G的权重为0.333×0.083=0.028。

2.3 建立考虑权重和排序比的综合评价模型

经典的加权平均模型如公式（3），其中k为评价指标个数，xi为F在指标qi上的指标值，φi为指标qi对应的权重系数，S为个体F在加权平均模型下的综合评价值。

加权平均模型考虑了评价指标的重要性和被评价单位在该指标上的评分两个因素，但是加权平均模型无法体现出被评价个体在群体中同一指标上的相对优劣情况。

比如：两个被评价单位F1和F2在权重相同的两个评价指标B1和B2上的评分均为90分，利用加权平均模型在综合评分中看不出两者区别。但是F1的90分位于100个评价个体中的前1%，而F2的90分位于100个评价个体中的后1%。如何在加权平均模型基础上体现出被评价个体在全体中的相对表现情况，我们引入一个排序比因子，并将排序比因子、权重和评分3个因素综合考虑构建评价模型。

定义1（排序比因子）：设被评价群体个体总数为N，待评价个体为F，F在指标q上的得分值为s，群体中指标q上得分值低于s的个体个数为N(F,q)，则F在指标q上的排序比因子Q(F,q)为：

综合考虑权重和排序比因子的综合评价模型如公式（5）：

其中Snew为个体F在综合模型下的综合评价值，k为评价指标个数，xi为F在指标qi上的指标值，φi为指标qi对应的权重系数，Q(F,qi)为个体F在指标qi上的排序比因子值，λ为排序比因子对评价结果的影响程度参数，由人工设定。当λ=0时，综合模型等价于加权平均模型。

以表4的数据为例，共有F1～F4四个参评单位，q1～q4四个评价指标，F1～F4 在q1～q4的评价结果分为A、B、C、D四个等级。q1～q4四个评价指标的权重分别为0.2、0.3、0.3、0.2，λ设为0.2，等级A～D对应的分值分别为100、80、60、40。则加权平均模型下F1的综合评价值为

S=0.2×80+0.3×80+0.3×100+0.2×60=82 ；综合权重和排序比模型下F1的综合评价值为

类似地，可以计算出F2～F4在两个模型下的综合评价值，见表4。

表4 两个评价模型的评价结果

从表4中可以看到，利用权重和排序比综合模型可以进一步获得个体在群体中的相对表现，比如个体F1和F3，虽然两者的加权平均值相同，但是F1的综合模型值更高，表明F1在某些指标上具有更好的相对表现。同时，利用两个模型评价值之差，也可以判断出个体在群体中的相对表现的整体情况。差值越大，表明相对表现越好。

3 方法实现和应用情况

根据上述定义的指标体系和评价模型，实际应用中开发了本科教学状态数据采集平台，完成数据采集和质量评价。数据采集平台框架见图1。

数据来源于两个方面：一方面与学校教学管理系统对接，由系统自动收集各二级学院各年度的客观性教学状态基础数据，比如四级率、毕业率等；另一方面，需要专家评定打分的数据，由专家在平台在线进行评分。最后依据本文模型进行二级学院本科教学质量的综合评价。

图1 教学基础数据采集平台框架

我们所提方法在我校已经进行了实际应用，对教学管理发挥了较好的支持作用。方法有如下优势：①评价指标体系比较完整地概括了学校的主要教学质量监测点，也受到被评价单位的认可。层次化的指标体系与专家的指标设定习惯相符，易于扩充和变更，1-9标度法的定性比较适合以专家经验为基础的初值设定。②利用AHP评价方法将定性和定量结合起来的优势，在专家定性比较的基础上给出量化的权重值，能够既充分发挥专家的宏观判断优势，又能弥补专家精确数值量化评价的困难，适合教学这样复杂系统的特性。③在加权平均模型的基础上引入排序比因子构建评价模型，评价人员不仅能获得个体的总体表现，同时能够获得更多的个体在群体中的相对表现信息。