不确定航迹自适应预测模型

2019-05-24崔亚奇熊伟何友

航空学报 2019年5期

崔亚奇，熊伟，何友

海军航空大学信息融合研究所，烟台 264001

航迹预测主要是基于目标历史运动航迹，对目标未来可能的位置进行预测，是当前进行正确判断和科学决策的主要依据。作为一项极为关键的基础支撑技术，航迹预测在民用和军事领域具有广阔的应用场景[1-3]。例如，在民用领域，对船舶的航迹趋势做出正确的判断，就可以采取相应的措施，趋利避害，使目标船舶和附近其他船舶处于安全的运行环境中，对民航飞机航迹进行精确的预测，就可以提高空中交通管制的效率，提供及时、最优的冲突解决方案，提高空域容量。在军事领域，目标航迹预测更是贯穿目标识别、目标跟踪、目标打击等作战全环节当中，譬如可用于异常航迹检测，识别不明目标；可用于雷达目标跟踪，提高目标跟踪连续性；可以用于导弹对移动目标火力打击，提高导弹命中概率等。

鉴于目标航迹预测技术重要作用和广泛需求，当前对目标航迹预测技术进行了多方面、多角度的研究尝试，取得了大量研究成果。根据是否需要对目标运动模型进行建模，现有航迹预测技术可分为无模和有模两大类。其中，无模技术把航迹预测问题单纯地视为时间序列预测问题，忽略问题领域知识，直接选取匹配的方法进行预测，譬如基于灰色模型的航迹预测方法[4]，基于BP神经网络的航迹预测方法[5-6]等。此类方法具有前提假设少、模型简单、所需样本数据少的优点，但对所采用时序方法的合理性，与实际问题的契合性，缺乏必要理论论证。同时由于所采用时序模型较为简单、能力有限，现有无模类方法还存在适用范围窄、泛化能力弱、预测精度低的问题。

有模技术则基于假定的目标运动模型，采用统计估计理论，对航迹进行预测。根据假定的目标运动模型数量，有模技术还可进一步划分为单模[7-9]和多模两大类[10-13]。单模技术基于目标仅做一种模式运动的假设进行航迹预测，常见的目标运动模型有匀速、常加速、协同转弯、Singer、当前统计和Jerk等模型，相匹配的统计估计方法有卡尔曼滤波[7]、扩展卡尔曼滤波[8]、粒子滤波[9]等。多模技术[10-13]则假定目标依据一定概率，按照模型集里面的有限运动模式进行交替运动，其假定的模型集一般比较小，主要包括匀速、常加速、协同转弯等3种模型，相匹配的统计估计方法有交互多模型和高斯和等。有模技术具有理论严谨，性能有保证，实现简单的优点，但由于实际目标运动模型未知多样，此类方法存在先验假设过多，前提条件严苛的问题，进而导致其适用范围有限、通用性差，实际运用效果时好时坏。虽然多模方法一定程度上弱化了目标模型假设，但与实际情况仍存在较大差距，尚没有完全有效解决问题。

综上所述，现有航迹预测技术存在的问题可归纳如下：

1) 无模技术假设简单、通用性强，但其合理性目前缺乏理论分析支持，同时现有方法采用的时序模型较为简单、能力有限，存在适用范围窄、泛化能力弱、预测精度低的问题。

2) 有模技术理论严谨、性能有保证、实现简单，但存在先验假设过多、前提条件严苛的问题，实际运用效果时好时坏、通用性差。

针对上述问题，研究提出不确定航迹自适应预测模型。该模型具有无模与有模两类技术的优点与长处，具备理论严谨、先验假设少、适用范围广、通用性强的优点，无需对目标可能的运动模型进行提前明确，适用于目标运动具有规律性、但具体运动模式不确定的航迹预测问题，可完全有效解决航迹预测问题。

本文首先通过理论推导，构建不确定航迹自适应预测基本理论框架，然后基于神经网络，建立不确定航迹自适应预测(Uncertain Track Adaptive Forecast, UTAF)模型，并生成典型的实现方法，最后通过仿真与实测数据，对其有效性进行验证。

1 模型研究

首先对需要解决的问题进行描述建模，然后根据实际情况，进行合理必要假设。基于此，利用全概率公式，构建问题的基本解决框架，最后采用神经网络设计出有效的模型。

1.1 问题建模

航迹预测主要是由前多个时刻的位置，预测下一时刻的位置。从概率的角度看，航迹预测就是要求取p(yt+1|{x1,x2,…,xt})，并进行最大化，以得到

(1)

1.2 基本假设

受目标自身性能、或操纵人员习惯、以及其他外部条件影响限制，目标在运动过程中存在一定的规律，并不是毫无章法、随机运动的，譬如受目标自身性能限制，目标的最大加速度、最小转弯半径、巡航速度基本上是确定的，受操纵人员习惯和其他外部条件影响，目标何时加速、何时减速、何时转弯、加速方式、减速方式等，也有特定规律。因此，目标运动是有模式的，但什么类型的目标，具有什么样的运动模式，相应运动模式的多少、规模以及具体内容，以及目标在何时以何种模式运动，对预测者来说，是不确定的，也是难以确定的。

假设目标以一定模式c运动，并且目标下一时刻的位置完全由当前的模式c确定，即

p(y|c,{x1,x2,…,xt})=p(y|c)

(2)

式中：c为实数向量，包含所有与预测下一时刻相关的信息，由c构成的空间{c}为目标运动模式空间，表示目标所有可能的运动模式。

1.3 基本框架

对于条件概率p(y|{x1,x2,…,xt})，由全概率公式，可得

p(y|{x1,x2,…,xt})=

p(c|{x1,x2,…,xt})

(3)

基于假设，根据式(2)，可进一步得到

p(y|{x1,x2,…,xt})=

(4)

(5)

(6)

I({x1,x2,…,xt})

(7)

(8)

式中:I-step主要是根据前多个时刻的位置提取目标可能的模式信息，而E-step则根据模式(8)信息，对目标可能的预测位置进行估计生成。

1.4 模型设计

如果能根据I-step和E-step过程的信息处理特点，直接设计出既具有相应功能特征，又不涉及目标具体运动模式，同时还能方便求解的一般表示，则可构建UTAF模型，如图1所示。

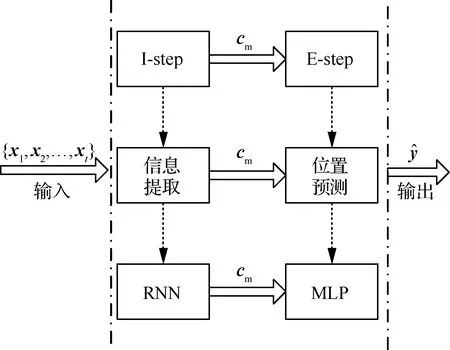
图1 不确定航迹预测思维图Fig.1 Thinking map of uncertain track forecast

鉴于神经网络强大的信息提取、模式识别和函数逼近能力，考虑采用神经网络结构对I-step和E-step进行一般表示：

1) 循环神经网络(Recurrent Neural Network, RNN)是专门处理变长序列数据的网络结构[14-16]，具有强大的信息记忆、信息提取、信息表示以及模式识别能力，因此可采用RNN对I- step进行一般表示:

hi=f(xi,hi-1)

(9)

c=q({h1,h2,…,ht})

(10)

2) 多层神经网络(Multi-Layer Perceptron, MLP)具有很强的函数逼近能力，两层MLP即可逼近任意一个连续函数[17-21]，因此可采用MLP对E-step进行一般表示:

(11)

因此，用RNN表示I-step，用MLP表示E-step，串联起来，即为UTAF模型，如图2所示。

与现有航迹预测模型方法相比，UTAF模型具有如下显著特点：

1) 几乎不存在任何先验假设，唯一要求是目标运动有模式，即目标运动事件本身是可预测的，这与实际情况是相符的。

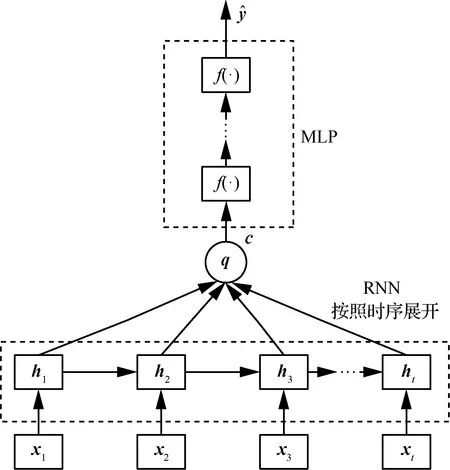
图2 UTAF模型Fig.2 UTAF model

2) 推导严谨，有理论支撑。

3) 采用神经网络结构，模型表达能力强，涵盖维度高，泛化能力强。

4) 能利用大量历史观测数据进行模型训练，符合当前大数据、人工智能技术发展潮流。

2 典型方法

基于已建立的通用模型，采用具体RNN和MLP结构，通过参数寻优，构建生成典型不确定航迹自适应预测方法(Basic Uncertain Track Adaptive Forecast Method, Basic-UTAFM)。

首先，采用典型RNN结构，实现I-step。典型RNN结构包括Simple-RNN，LSTM(Long Short-Term Memory)以及GRU(Gated Recurrent Unit)等不同网络结构。其中Simple-RNN存在长时间信息衰减问题，LSTM与GRU则通过门结构建立了长时间信息保持通道，可有效保留提取长时间信息，并且相对于LSTM，GRU结构更加简单有效。因此这里采用GRU，详细构建如下:

(12)

(13)

ri=σ(Wrxi+Urhi-1)

(14)

zi=σ(Wzxi+Uzhi-1)

(15)

式中：运算∘表示对应元素相乘；σ为Sigmoid函数；hi、ri、zi∈Rn，hi为RNN第i时刻隐藏层向量,ri、zi为相应时刻的重置门和更新门；n为隐藏层单元数量，代表GRU的表示能力；W、Wr、Wz∈Rn×o、U、Ur、Uz∈Rn×n为权重矩阵；o表示输入层xi的维度。

需要说明的是，为了简化表达，在式(13)～式(15) 中，省略了偏置项。在MLP层，按照相同的原则进行处理，不再另行交代。

由于ht基本包含了历史观测{x1,x2,…,xt}模式信息，可以把其直接作为模式，即

c=q({h1,h2,…,ht})=ht

(16)

然后，采用典型MLP结构，具体实现E- step。由于GRU结构已经包括一定量非线性单元，MLP可以采用简单的一层结构进行目标位置预测，即

(17)

式中：Wy∈Ro×n为权重矩阵。

最后利用训练数据集，通过参数训练优化，生成典型的不确定航迹自适应预测方法。由于航迹预测是回归问题，可采用均方差作为损失函数，如式(18)，而后利用梯度下降法进行W、U、Wr、Ur、Wz、Uz、Wy权重矩阵参数和偏置项参数寻优。另外训练数据集主要通过历史观测数据来构建，在构建时，应注意数据的广泛性和规范性。

(18)

采用简单的一层RNN和两层MLP结构，示范性生成了Basic-UTAFM。在实际运用中，应根据问题的复杂程度，参照神经网络模型设计、调节、优化的步骤和方法，依据数据验证结果，对RNN基本结构，RNN和MLP层数，每层神经元个数，激励函数类别、正则化、Dropout等影响神经网络性能的主要配置与选项进行选择和优化。

3 实验验证

为充分验证UTAF模型的有效性，分别进行仿真实验和实测实验，并与Baseline方法进行性能分析比较，其中仿真实验主要验证UTAF模型是否具备多模航迹预测能力，实测实验主要是在实际问题中对模型的性能表现进行验证分析。Baseline方法采用时间序列预测中的Persistence Algorithm，用t时刻数据预测t+1时刻数据。

整个实验主要采用Python语言，基于Keras和Tensorflow深度学习库，进行UTAF建模、训练、优化，以及与Baseline的性能比较分析。

3.1 仿真验证

用余弦、斜三角、阶跃、抛物线等常见基本函数，表示目标不同的运动模式，并以其为基础，混合构建4种不同数据集，分别为不同频率余弦数据集(Different Frequent Cosine data set, DFC)及添加噪声版(Different Frequent Cosine with Noise data set, DFCN)，不同类型函数数据集(Different Kinds Function data set, DKF)及添加噪声版(Different Kinds Function with Noise data set, DKFN)。每种测试数据集包含4 000条训练数据，每种模式1 000条，打乱混合在一起，具体构建方法见表1。其中仿真数据集每条数据的具体构成方法为：按照200 Hz的采样频率对不同模式函数进行采样，每种模式的连续7个点作为一条训练数据，前6个点为输入，第7个点为输出。

对于4种不同数据集，分别进行Basic-UTAFM的训练、验证和测试。由数据集的构成可知，Basic-UTAFM输入和输出维度o=1，设置RNN隐藏层神经单元数量为n=10。数据集按照9:1比例划分为训练集、验证集，采用Adam(Adaptive moment estimation)寻优方法，按每批10条数据进行Basic-UTAFM参数更新，共训练遍历20次数据集。

首先，以情况较为复杂的DKFN数据集为例，通过直观展示预测结果，进行Basic-UTAFM预测性能定性分析，如图3所示。基于DKFN数据集，训练生成的Basic-UTAFM，能对数据集里面的阶跃函数和抛物线函数进行较为准确的预测，对其他两个函数的预测结果类似。同一个Basic-UTAFM，相同的参数配准，清晰地表明了UTAF和Basic-UTAFM能提取识别数据的模式信息，并基于模式进行预测。

进一步对Basic-UTAFM预测性能进行定量分析。Basic-UTAFM在不同数据集的训练误差曲线如图4所示，Basic-UTAFM预测均方误差(MSE)如表2所示。在表2中，性能提升数据列是表示相对于Baseline，Basic-UTAFM预测精度提升的百分比，其计算公式为(1-MSEBasic-UTAFM/MSEBaseline)×100，单位为%。

表1 仿真数据集Table 1 Simulation datasets

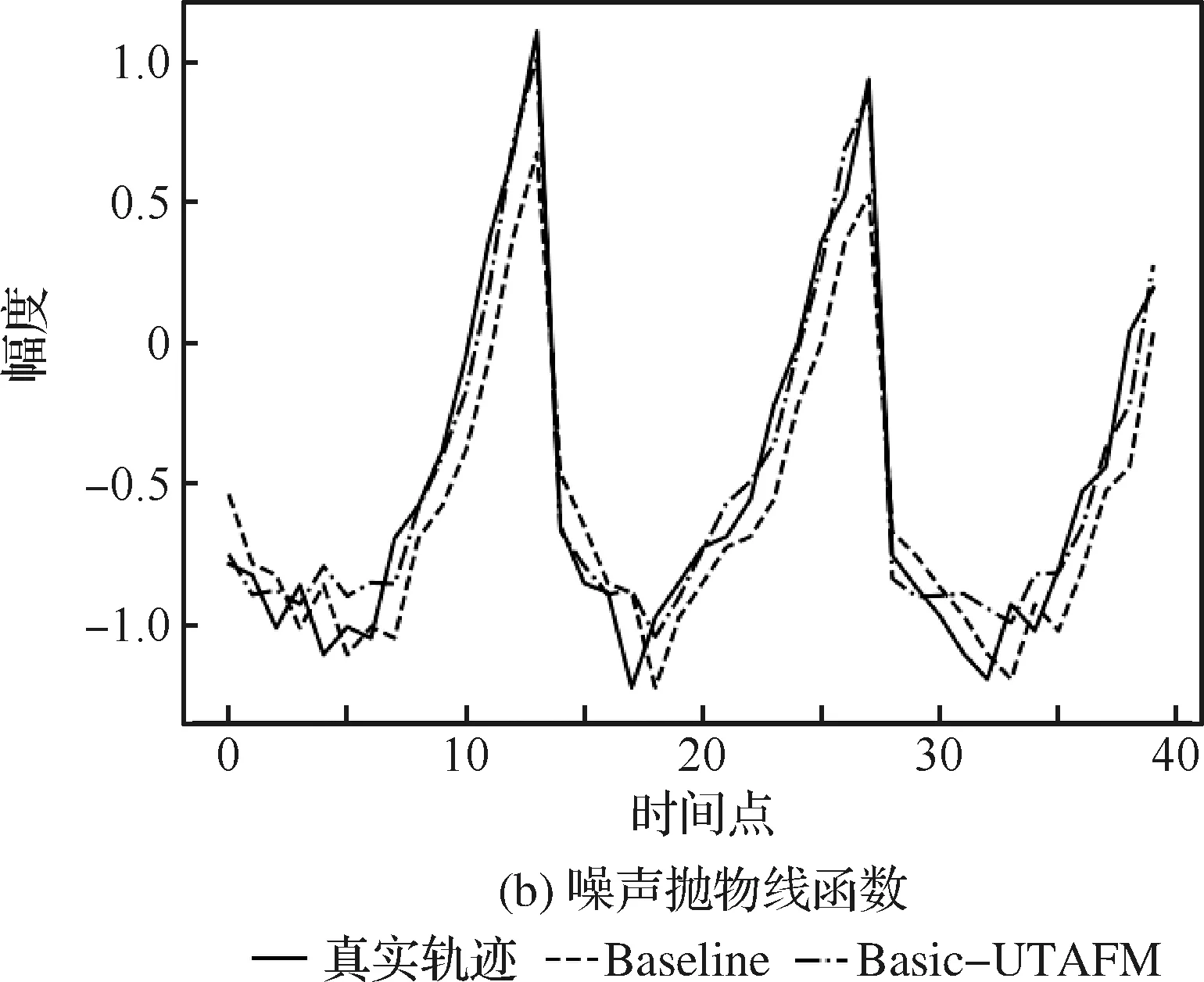
图3 Basic-UTAFM与Baseline预测结果对比Fig.3 Comparison of forecast results between Basic-UTAFM and Baseline method

由图4和表2可知，Basic-UTAFM在4种数据集下均能得到收敛的结果，并且与Baseline方法相比，预测性能提升明显：① 在DFC数据集上，误差曲线下降趋势明显，训练曲线与验证曲线基本重合，与Baseline相比，性能提升99.86%，表明在数据变化连续、模式清晰可辨的情况下，Basic-UTAFM具有很好的预测效果；② 在DFCN数据集上的表现，与DFC数据集上基本相同，但由于噪声的影响，模式的可辨性变差，性能存在一定程度下降，变为69.24%，并且在模式1数据上性能提升为-15.11%，分析主要是由于“模式1”周期为1 Hz，在相同200 Hz数据采用频率下，相邻时刻采样点间数值差别较小，如果进一步受噪声影响，则相邻时刻数值表现为来回摆动，变化趋势微弱、不明显，模式不易被Basic-UTAFM识别，导致模式1预测存在一定困难，Basic-UTAFM预测性能有一定程度下降问题。但是可以肯定，在噪声情况下，如果数据模式仍旧可辨，则Basic-UTAFM仍能取得较好的预测效果；③ 在DKF和DKFN数据集上，误差曲线下降趋势同样比较明显，与Baseline相比，性能分别提升36.37%和33.61%。但验证曲线围绕训练曲线存在一定上下波动，表明此类数据集下，Basic-UTAFM在部分数据上有较差表现。结合表2可知，Basic-UTAFM主要是对模式2阶跃函数的预测效果差，相对于Baseline，性能仅提升16.57% 和17.61%，不及整体平均水平。分析主要是由于阶跃函数存在突变，模式辨别存在困难所导致的，而噪声情况下性能1%的提升，也主要是由于噪声一定程度上缓解了阶跃函数突变效果的原因。

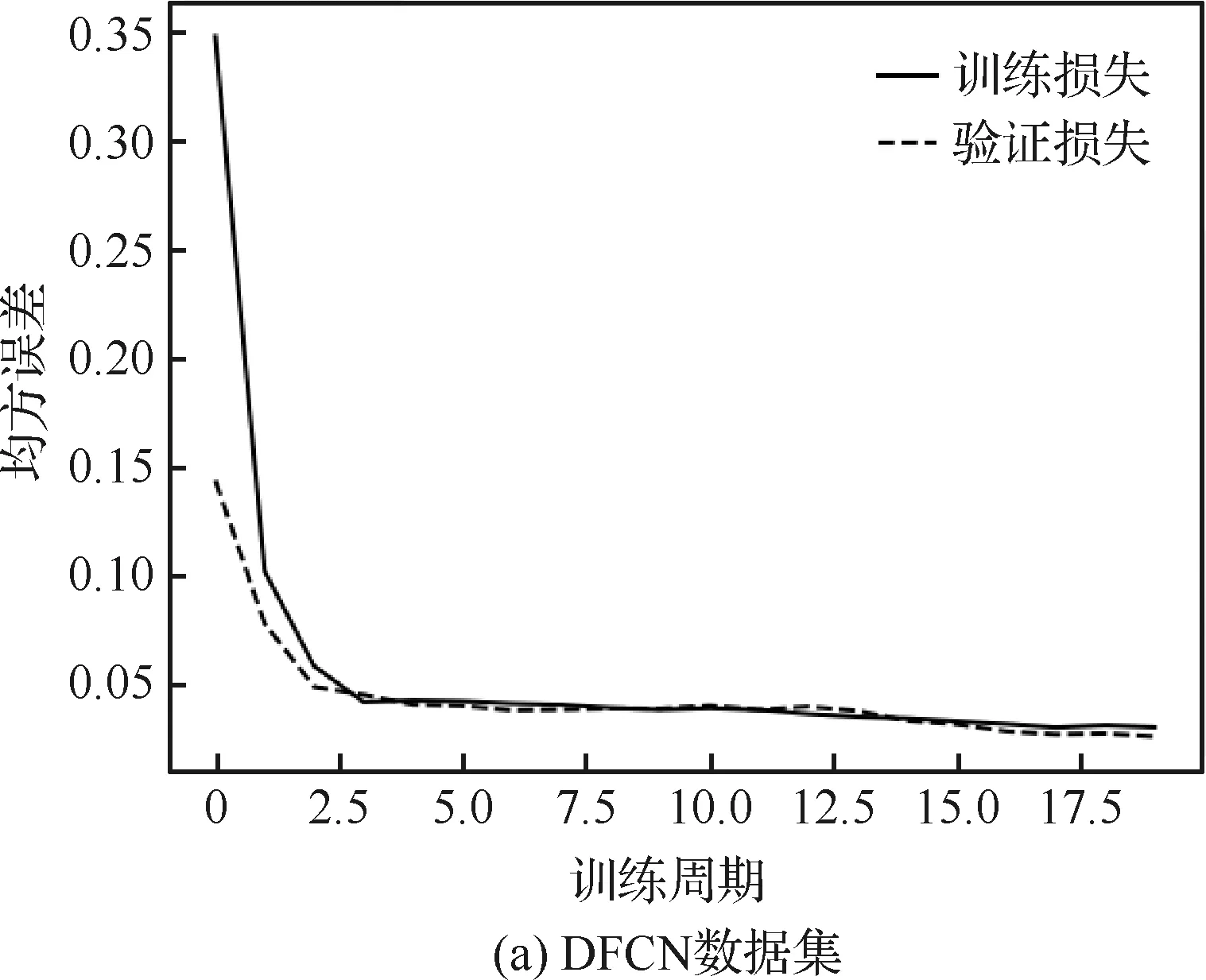
图4 不同数据集下Basic-UTAFM训练误差曲线Fig.4 Curves of basic-UTAFM training error using different datasets

进一步，DFC数据集下100次蒙特卡罗仿真结果如图5所示。可知，除了在模式1数据上，存在少量与Baseline性能相当的异常点外，Basic-UTAFM在大部分仿真中对模式1预测性能，所有仿真对其他模式预测性能，和在所有仿真中的整体预测性能，均明显优于Baseline，有力地说明了Basic-UTAFM的有效性和稳定性。

表2 Basic-UTAFM预测性能比较(仿真数据)Table 2 Comparison of Basic-UTAFM with baseline forecast performances (simulation data)

下面对Basic-UTAFM训练耗时和预测耗时进行分析，如表3所示，共设置4种不同大小数据集，采用与上面相同的模型设置和训练设置，每个数据集上训练模型20次，训练所用计算机CPU为至强E5-1620 v4 3.5 GHz，内存为16 G，没有利用GPU加速运算。

由表3可知，当数据集大小为4 000时，总训练耗时、单次训练耗时和每1 000次的预测耗时分别为74.24、3.71、0.110 s，训练耗时大，预测耗时很小，并且随着数据集增大，训练耗时线性增加，而预测耗时有一定程度下降，稳定在0.063 s，符合神经网络训练特点。按照神经网络实际运用方法，由于模型训练耗时比较大，预测耗时比较小，可以在线下对模型进行训练，训练成功后，在线上进行部署预测。

图5 DFC数据集下100次蒙特卡罗仿真Basic-UTAFM预测MSE箱形图Fig.5 Basic-UTAFM MSE boxplot through 100 Monte Carlo using DFC dataset

表3 Basic-UTAFM耗时分析Table 3 Basic-UTAFM time-consuming analysis

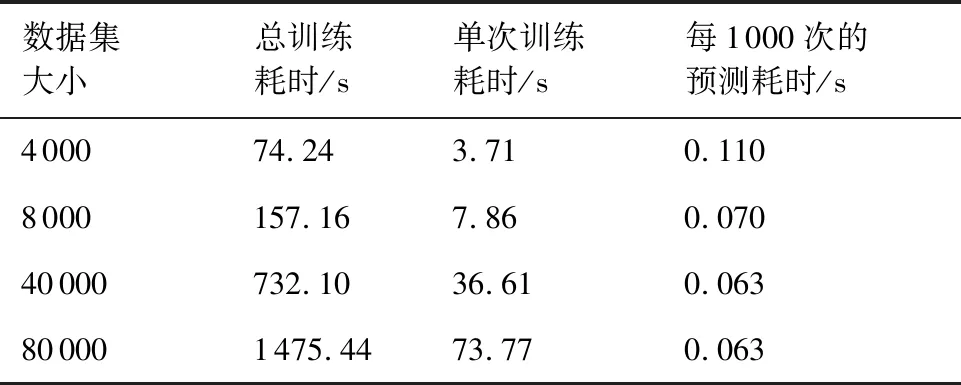
数据集大小总训练耗时/s单次训练耗时/s每1000次的预测耗时/s400074.243.710.1108000157.167.860.07040000732.1036.610.063800001475.4473.770.063

综合上述分析，可以肯定：在数据集包含多种模式，并且不同模式间清晰可辨情况下，UTAF模型和具体Basic-UTAFM能很好地提取识别出数据模式，并基于模式，进行正确有效地预测。

3.2 实测验证

进一步，通过民航飞机空中位置预测，对UTAF模型和具体Basic-UTAFM进行实测数据验证。由于飞机当前航迹点位置是由上时刻位置、加航速与时间差乘积得到的，存在确定趋势，是非平稳的，不能直接作为神经网络输入，而飞机航速的变化是平稳的，因此这里通过对航速的预测，来实现飞机航迹的预测，同时由于经度方向速度和纬度方向速度基本是不相关的，可以对其进行分别预测。

利用ADS-B设备，采集民航飞机航行轨迹数据，见图6，构建民航飞机航迹数据集(Civil Aviation Flight Track data set, CAFT)，具体构建方法见表4。其中Tmax表示所有航迹内航迹点间的最大时间间隔。航迹点间时间间隔越小，航速可能的变化也就越小，信息的不确定性相应也比较小，因此需要根据Tmax把CAFT分成存在包含关系的5类数据集，即CAFT-60包含CAFT-50、CAFT-50包含CAFT-40等。另外，在实际训练时，还需要设定最大航速，对航速数据进行归一化处理，把航速限定在[0,1]或[-1,1]范围内。其中实测数据集每条数据的具体构成方法为：对每条目标航迹，按照时间先后，求取经度方向和纬度方向航速序列，然后顺序取6个连续时刻航速数据作为输入，相邻的后一个航速数据做输出，进而构成一条数据，一条目标航迹可构成多条数据。

表4 民航飞机航迹数据集Table 4 Civil aviation flight track data set

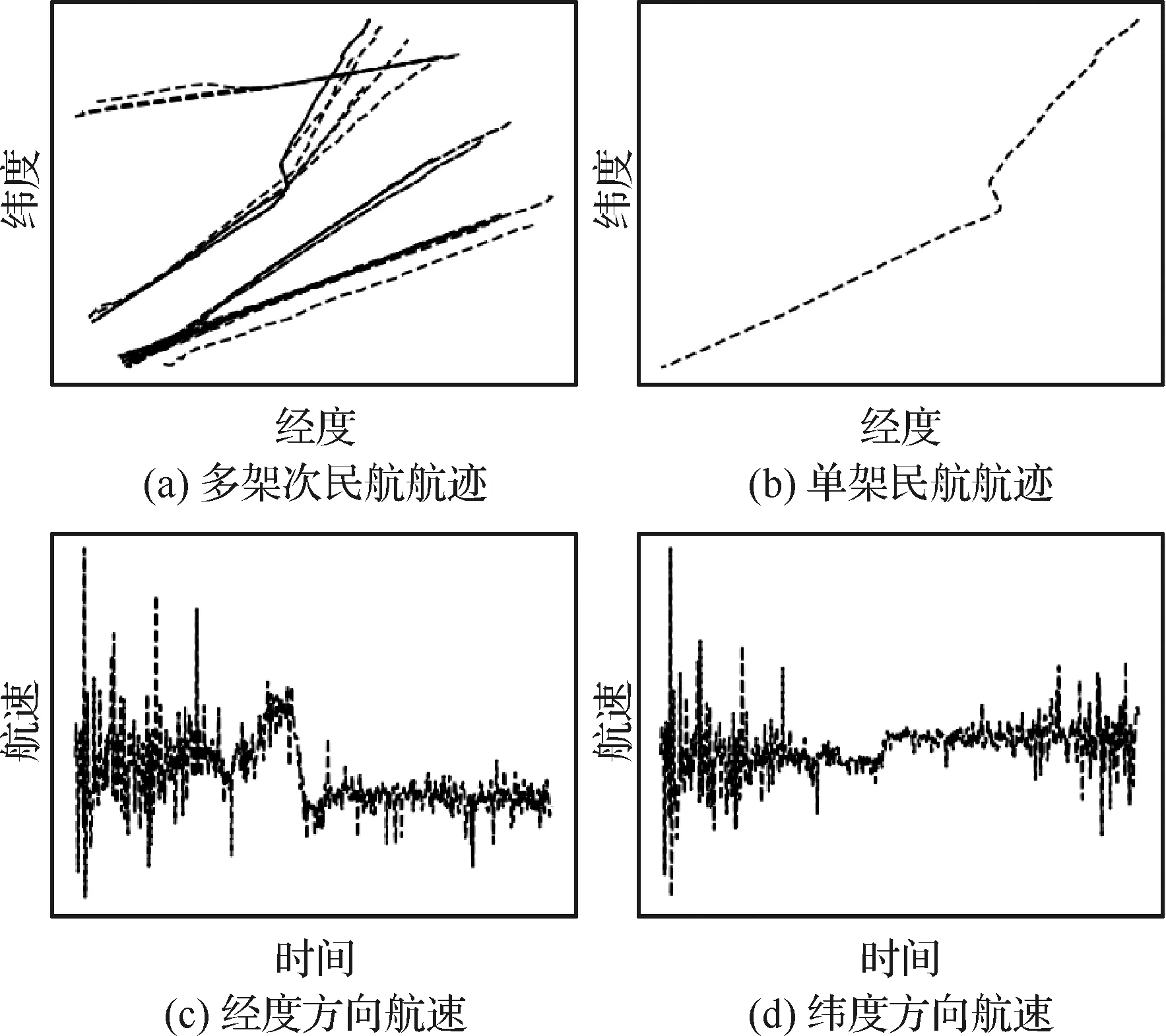
图6 民航飞机航迹和航速示意图Fig.6 Schematic diagram of civil aviation flight track and velocity

对于5类CAFT数据集，分别进行Basic-UTAFM的训练、验证和测试。由数据集的构成可知，Basic-UTAFM输入和输出维度o=1，设置RNN隐藏层神经单元数量为n=10。采用Adam自适应寻优方法，按每批5条数据进行Basic-UTAFM参数更新，共训练遍历10次数据集，Basic-UTAFM在CAFT-20数据集下的训练过程误差曲线如图7所示。由图可见，Basic-UTAFM收敛速度快、稳定性强，训练曲线与验证曲线也基本吻合，表明Basic-UTAFM能实现飞机航迹的预测，能解决实际的航迹预测问题。

Basic-UTAFM预测MSE如表5所示，其中纬度方向和经度方向航速分别采用两个不同的Basic-UTAFM进行预测，合成表示两个Basic-UTAFM对绝对速度的预测结果，即对纬度方向与经度方向速度的L2范数的预测结果。

由表5可知，Basic-UTAFM在5类实测数据集，10个航速预测问题中均能得到良好的结果，并且与Baseline方法相比，最低提升30.91%，最高提升36.87%，大部分提升33%左右，预测性能提升明显。

综合上述分析，实测实验结果有力地表明Basic-UTAFM具有较强的适应性，能有效地解决不同实际环境中的航迹预测问题，效果明显。

图7 CAFT-20数据集下Basic-UTAFM训练误差曲线Fig.7 Curves of Basic-UTAFM training error using CAFT-20 dataset

表5 Basic-UTAFM预测性能比较(实测数据)

Table 5 Comparison of Basic-UTAFM with baseline forecast performance (measured data)

名称类别Basic-UTAFM/10-2Baseline/10-2性能提升/%CAFT-20纬度1.752.7836.87经度1.462.1230.91合成1.873.1440.44CAFT-30纬度1.492.2533.83经度1.372.0533.11合成1.572.5638.65CAFT-40纬度1.241.8432.58经度1.171.7633.36合成1.241.9436.37CAFT-50纬度1.081.6132.47经度1.191.7331.53合成1.101.7236.13CAFT-60纬度1.031.5232.03经度1.131.7233.99合成1.001.6238.17