基于Kriging模型梯度解析解的改进一次二阶矩方法

李宝玉，张磊刚，裘群海，余雄庆

1. 南京航空航天大学 航空宇航学院，南京 210016 2. 中国运载火箭技术研究院，北京 100076

一次二阶矩(First Order and Second Moment, FOSM)方法是结构可靠性分析中一种简单易操作的方法，作为一种实用方法在工程问题中得到了广泛应用[1-3]。FOSM方法的基本思想就是将非线性的功能函数进行线性化，然后通过输入变量的一阶矩和二阶矩来计算线性化后的功能函数的一阶矩和二阶矩，使用其求得结构可靠度指标，进而近似得到功能函数的失效概率。随着方法精度的研究与发展，FOSM方法包括均值一次二阶矩(Mean Value FOSM，MVFOSM)方法和改进一次二阶矩(Advanced FOSM, AFOSM)方法。MVFOSM方法和AFOSM方法的区别在于二者线性化的点是不同的，前者是在输入变量的均值点处对功能函数进行线性化，而后者则是在对失效概率贡献最大的点，即最可能失效点—设计点处线性化。由于设计点是对失效概率贡献最大的点，因此在设计点处线性展开比在均值点处线性展开对失效概率的近似具有更高的精度[3]。

值得注意的是，不论是AFOSM方法还是MVFOSM方法，对于非线性功能函数问题，2种方法均需要将非线性功能函数进行线性展开，因此均需要求解功能函数的导函数，获取功能函数对各输入变量的梯度信息。对于显式功能函数，其导函数求解较为容易，而对于复杂工程结构可靠性分析中常见的隐式功能函数问题，其导函数则较难求解。有限差分法是求解隐函数的导函数的通用方法，但对于高度非线性问题，有限差分法的步长较难确定，而且计算梯度信息所花费的计算量相当大，特别地，对于以有限元形式表征的功能函数而言计算代价在工程问题中难以接受。

鉴于AFOSM方法的工程适用性，同时考虑到Kriging代理模型技术在结构可靠性工程及优化领域的应用广泛性，本文研究并提出了一种基于Kriging代理模型的AFOSM可靠性分析方法。在众多代理模型中，Kriging模型是一种应用较为广泛且精度较高的代理模型[4-9]。例如：Simpson等[6]将Kriging与响应面法的计算精度与计算效率进行了对比，并将其应用于航天飞机的设计中；Sakata等[7]改进和发展了抽样方法，并将Kriging模型应用于薄壁管和机翼等结构的优化设计中；Lucifredi等[8]将动态Kriging模型与神经网络进行了对比，然后将其应用于水电力系统的预测维护中。Kriging模型可以表示为张量积基函数的形式[10-11]，因此可以通过张量积基函数来解析地推导功能函数对输入变量导函数的表达式，进而利用较少的训练样本得到较高精度的Kriging代理模型后，直接得到功能函数对输入变量梯度信息的近似解，也即以较高的效率为AFOSM提供了较高精度的梯度信息，很好地解决了隐式问题梯度信息难以获取的难题。

1 改进一次二阶矩方法

(1)

(2)

设功能函数的均值和标准差分别为μg和σg，上述线性极限状态方程的可靠度指标βR和失效概率Pf可以由式(3)和式(4)精确求解[3]：

(3)

Pf=Φ(-βR)

(4)

式中:Φ(·)为标准正态分布的累积分布函数。

对于输入变量为非正态分布的情况，Rackwitz和Fiessler[12]提出了一种等价正态变量算法，简称为R-F法，将非正态变量转化为等价的正态变量，然后再采用AFOSM法求解可靠度指标，进而得到失效概率。

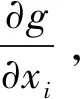
2 Kriging代理模型的梯度解析解

Kriging代理模型是一种半参数插值技术，Sacks等[4]将Kriging模型表达为线性回归部分和非参数部分2部分组成，即

g(x)=fT(x)β+Z(x)

(5)

式中：f(x)=[f1(x)f2(x)…fm(x)]T为输入向量x的多项式基函数，可以是0阶、一阶或二阶多项式，提供模型模拟的全局性近似；β=[β1β2…βm]T是需要确定的回归系数，m为线性回归部分基函数的个数；Z(x)为随机过程实现的非参数部分，提供线性回归部分fT(x)β的偏差，服从N(0,σ2)的正态分布，协方差为

Cov[Z(xi),Z(xj)]=σ2R(xi,xj)

i,j=1,2,…,N

(6)

式中：xi与xj为第i和第j个训练样本点；N表示训练样本点个数；σ2是随机分布误差的方差；R(xi,xj)为表征训练样本点之间的空间相关性的相关函数，表达为

(7)

式中：n是输入向量x的维数；xik和xjk分别为向量xi和xj的第k个分量；τk是相关性参数；d决定了函数在第k个坐标方向的光滑性。Kriging模型中的一元相关函数有多种形式[4-5]。

未知参数β和σ2可以通过式(8)和式(9)进行估计：

(8)

(9)

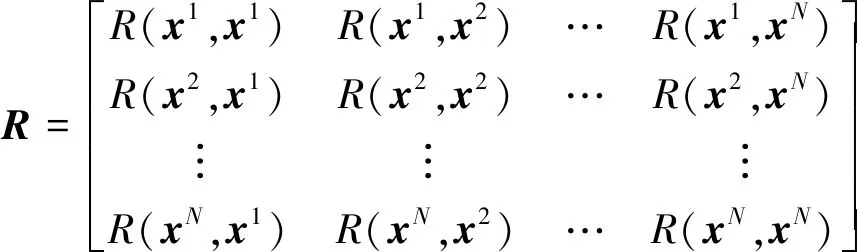
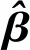
(10)

Kriging模型对于结构输入输出关系具有较高的拟合精度，已经被广泛运用于结构可靠性分析与优化设计中。关于模型详细的描述，可以参阅文献[4]。

Kriging模型表达为张量积基函数为[5,10]

(11)

式中：λi(i=0,1,…,N)为常系数。在Kriging模型的多种相关函数中，Gaussian相关函数被广泛选择使用，即hik(xk)=exp(-τk(xk-xik)2)，τk为变量xk对应的相关参数。式(11)中，Kriging函数的多项式基函数取0阶，因此，本文所采用的Kriging模型解析表达式为

(12)

分别对式(12)中等号两边输入变量xq求导数，推导如下：

(13)

3 基于Kriging解析解的可靠性分析方法

本文提出一种基于Kriging解析解的AFOSM可靠性分析方法，传统AFOSM方法中的导函数梯度信息由Kriging模型解析求得。值得注意的是，要采用改进的一次二阶矩方法求解可靠度指标和失效概率，必须先知道设计点。显然对于一个给定的非线性功能函数，其设计点是不可能预先知道的，这就必须采用迭代或者直接寻优的方法来进行问题的求解，一般是通过迭代前后两次的可靠度指标的相对误差满足设定的精度要求为止。对于成熟的AFOSM的迭代求解步骤的详细信息可查阅文献[3]。本文所提方法的简要步骤如下文所述，流程图如图1所示。

1) 鉴于拉丁超立方抽样(Latin Hypercube Sampling, LHS)[13]样本具有低偏差特性，采用LHS方法产生N个训练样本点构建Kriging模型。

图1 可靠性分析流程图Fig.1 Flow chart of reliability analysis

4) 采用式(4)求解结构失效概率。

4 算例分析

本节将所提的基于Kriging解析解的AFOSM法应用于数值及工程算例中以验证所提方法的正确性。4.1节利用简单的数值算例来验证所推导的Kriging梯度解析函数的正确性。4.2节将所提的基于Kriging解析解的AFOSM法应用于某航空发动机涡轮盘模型的可靠性分析中，以验证所提可靠性分析方法的正确性与高效性。在此基础上，4.3节将其应用于以有限元隐式形式表征的某导弹舵面结构的可靠性分析中，进一步验证本文所提方法的正确性与工程适用性。

4.1 数值算例

考虑2个非线性功能函数g1(x)和g2(x)，均包含4个基本随机变量xi(i=1,2,3,4)，且均服从正态分布xi～N(1,0.12)。功能函数表示为

(14)

易得2个功能函数对各输入变量偏导数在其均值点处函数值的精确解分别为

(15)

运用式(13)所推导的Kriging梯度解析函数进行上述导数值求解，分别抽取一定数量的训练样本建立2个功能函数的Kriging代理模型，代理模型建立后，将输入变量均值点代入可直接得到相应的梯度信息如表1所示。

由表1所示的结果可以看出，本文所推导的Kriging梯度解析解具有较高的精度，通过对比验证了所推导的基于Kriging代理模型的梯度解析公式的正确性。同时可看出，借助于Kriging代理模型的优势，仅需要少量的训练样本即可以获得高精度的结果，计算代价小。

表1 数值算例的Kriging梯度解析结果

Table 1 Results of Kriging based gradient analysis of numerical example

项目导函数值误差/%训练样本Ng1(x)/x11.0000g1(x)/x23.0000g1(x)/x35.0000g1(x)/x47.000020g2(x)/x12.0030.15g2(x)/x25.9990.017g2(x)/x39.9970.03g2(x)/x414.0020.01425

4.2 航空发动机涡轮盘算例

本算例分别抽取50、100、300个训练样本点建立Kriging代理模型，获取相应的梯度解析结果，进而采用AFOSM法进行涡轮盘可靠性分析。从表3可以看出，3种情况下，采用本文所提的基于Kriging解析解的AFOSM方法的可靠性分析结果均与Monte Carlo(MC)方法比较吻合，验证了该方法的正确性。随着训练样本的增加，Kriging模型的精度也随之增加，相应的梯度解析解精度也随之增加。然而，随着训练样本数量的增加，可靠性分析结果的精度提高程度很小，可见Kriging模型本身已经具有较高的精度，然而其可靠性分析结果的结果受限于AFOSM方法本身的精度。

图2 某型航空发动机涡轮盘示意图[14]Fig.2 Schematic diagram of an aero-engine turbine disc[14]

表2 某型航空发动机涡轮盘模型输入变量分布信息

Table 2 Input variable distribution information of an aero-engine turbine disc

输入变量分布类型均值变异系数ρ/(kg·m-3)正态8 2400.1C/(kg·m)正态5.670.1A/m2正态6.2×10-30.1J/m4正态1.22×10-40.1n/(r·s-1)正态2000.05

表3 某型航空发动机涡轮盘模型可靠性分析结果

表3中所示方法的计算量也显示出基于Kriging解析解的AFOSM法的计算效率，针对一般工程问题，只需少量的计算成本即可得到较高精度的可靠性分析结果，很大程度降低了计算代价。

4.3 飞行器舵面算例

图3为某型飞行器舵面结构示意图[15-16]，其由5条桁条、6条翼肋、蒙皮以及用于和机体相连接的固定端所组成。各个部件的材料均为某钛合金材料，材料的杨氏模量为E，泊松比为ν。翼肋与桁条的厚度均为trs，蒙皮的厚度为tsk。在飞行器的飞行过程中，舵面用于调节以及稳定飞行姿态，其所承受的载荷主要为气动载荷，大小为P，垂直作用于上蒙皮。舵面结构材料的弹性模量、泊松比，桁条、翼肋、蒙皮的厚度以及所承受的气动载荷均为服从正态分布的随机变量，详细分布信息见表4。以舵面结构在承受气动载荷情况下的最大变形不超过δc=8 mm为门限值，建立结构系统的功能函数为

g(E,ν,P,tsk,trs)=δc-max(δ)

(16)

由于此算例为以有限元形式表征的隐式问题，舵面结构在气动载荷作用下的位移无法解析求解，本节采用有限元分析软件MSC.Patran/Nastran对结构的变形进行求解，有限元模型如图4[15-16]所示。一次响应计算时间较长，若采用Monte Carlo法进行可靠性分析，其计算代价是无法接受的。为了结果对比，在建立Kriging模型后，采用MC方法(Kriging_MC)针对建立的代理模型进行结构可靠性分析，以此结果作为参照解进行对比。

如图5所示，抽取200个训练样本建立舵面结构功能函数的Kriging代理模型，进而抽取106个样本代入建立的代理模型中进行舵面结构的可靠性分析，以此结果作为参照解。在抽取80个训练样本的情况下，采用本文所提方法的可靠性分析结果与参照解较为接近，再次验证了所提结构可靠性分析方法的正确性，结果的差异性主要来源于AFOSM方法本身对于高度非线性问题的适用性。然而值得指出的是，若直接采取数值模拟法进行有限元隐式问题的可靠性分析的计算代价是无法承受的，进行200次有限元模型分析同样需要花费较长时间，计算成本相对较高，本文方法在80次模型调用的情况下，所得结果精度较高，进而进一步验证了本文所提方法的工程适用性。

图3 某型飞行器舵面结构示意图[15-16]Fig.3 Schematic diagram of an aircraft rudder structure[15-16]

表4 某型飞行器舵面结构输入变量分布信息

Table 4 Input variable distribution information of an aircraft rudder structure

输入变量分布类型均值变异系数E/MPa正态1176000.1ν正态0.30.1P/MPa正态0.160.1tsk/mm正态10.05trs/mm正态30.05

图4 某型飞行器舵面结构有限元模型[15-16]Fig.4 Finite element model for an aircraft rudder structure[15-16]

表5 某型飞行器舵面结构可靠性分析结果

Table 5 Reliability analysis results of an aircraft rudder structure

方法失效概率计算量Kriging_ANA_AFOSM0.008980Kriging_MC0.0092200

5 结 论

1) 针对工程广泛应用的AFOSM法对于隐式功能函数问题存在梯度信息较难求解的现状，尤其是对于以有限元形式表征的工程复杂问题，梯度计算难度大、计算代价大，本文提出了基于Kriging模型梯度解析解的AFOSM可靠性分析方法，为AFOSM法提供了高精确的梯度信息，有效地解决了AFOSM方法的工程应用难题。

2) 鉴于Kriging模型在工程应用中的优势以及考虑到Kriging模型可以很好地表征为张量积基函数的形式，本文研究推导出了基于Kriging代理模型的功能函数对输入变量导函数的解析表达式，Kriging模型建立好后可直接得到梯度解析结果。

3) 本文提出的基于Kriging代理模型梯度解析解的AFOSM法拓宽了AFOSM方法的应用范畴，成为AFOSM方法的补充，为工程复杂问题的结构可靠性分析提供了可供选择的方法。算例验证了基于Kriging模型的梯度解析结果具有较高精度，因此，基于Kriging模型解析解的AFOSM方法的精度与适用性与AFOSM本身密切相关。