基于风险差分运算的电网调控操作风险快速评估研究

李功新， 李泽科， 林文彬， 陈建洪， 唐志军

(1. 国网福建省电力有限公司, 福建 福州 350003； 2. 国网福建省电力有限公司电力科学研究院, 福建 福州 350007)

0 引言

随着电力市场的改革和电力系统规模扩大， 电网结构必然呈现区域间互联、 远距离大容量送电、 交直流混合运行、 大规模新能源接入等特点， 电力网大多运行在临近安全极限的情况下. 操作越频繁， 误操作引起的事故也越严重. 由于工作人员缺少操作精度满足需求的工具， 只能依据工作经验进行调度决策， 目

前SCADA/EMS系统的原始数据大部分属于“仪表式”堆砌， 工作人员面对海量的电网运行“生数据”， 只能依托多年工作经验积累的大数据分析能力. 一旦发生紧急事故， 若工作人员单纯根据以往工作经验进行操作， 极可能错过事故处理操作的最佳时机， 若提前几秒操作就可能避免一次重大的事故； 有时可能所选择的操作措施并非本次事故的最佳操作方式， 导致调控操作的效果大大降低. 因此， 对调度操作风险进行量化分析， 可以为工作人员提供重要参考.

当前对电网调控操作的风险评估正处于高速发展的阶段， 现有研究针对电网调度运行过程中的调控操作风险问题， 基于相关风险评估理论， 并建立相关风险评估指标， 从安全性、 经济性、 电网质量等多方面量化事故所引发的后果， 以期建立风险评估模型， 并给出相应的解决措施[1-7]. 对电网的运行状态进行准确评估具有重要的实际意义， 国内外专家学者已在该领域做了相关的研究， 但仍然存在评估速度慢、 精度低、 模型不全面等一系列问题[8-13]， 因此本研究提出一种基于差分运算的电网运行状态快速评估方法， 以实现电网调控操作风险评估， 保证电网安全稳定运行.

1 风险评估理论及步骤

图1 风险理论示意图Fig.1 Schematic diagram of the theory of risk

风险理论的核心是评估风险因素对所分析系统产生的影响， 如图1实线箭头所示， 当某外在因素具备一定的概率分布特性， 且对该系统的存在状态产生影响时， 若系统存在若干条满足一定概率分布的发展轨迹， 则系统存在一定的不确定性风险. 若系统只有一条发展轨迹， 则该系统所有的影响因素都是明确的， 即不存在任何不明确的风险.

电网风险评估主要涉及以下5个步骤.

1) 建立系统元件的概率模型. 电力系统中存在大量的电源、 输配电线路、 变压器等元件， 每一类元件都有自己的计算模型， 而且都能基于马尔可夫模型进行模拟， 只是侧重点不同而已.

2) 选择系统状态并计算其概率. 选择系统状态的方法可以概括为两类， 一类是蒙特卡罗模拟法， 另一类是状态枚举法.

通常情况下， 大电网中所包含的元件不计其数， 因此要枚举所有的运行状态其工作量巨大， 且不易得出. 蒙特卡罗仿真法虽然能够得到较准确的运行结果， 但需要大量的计算， 计算过程时间长， 不是处理实际问题的最佳方式. 因此本研究采用枚举法.

3) 故障预扫描. 通过故障状态预扫描方法降低需要分析的故障状态数量， 缩短计算时间.

4) 评估系统故障状态的后果. 故障后果评估又称故障损失评估， 根据不同的研究对象， 其过程可能包括功率平衡， 系统的连通性及识别、 最优潮流、 电压稳定性控制等.

5) 计算风险指标. 根据步骤2)、 3)所计算的结果， 进行全局分析， 形成一套能够反映系统运行状态的风险评估指标， 基于不同的侧重点， 所计算的指标值也不尽相同. 研究针对实际电网进行风险评估， 因此将采用多个风险指标全面评估系统面临的风险.

2 基于风险差分运算的调控操作风险快速评估的指标体系

当前运行风险评估中风险指标的计算都是针对某一电网运行状态进行， 而调控操作风险评估与传统电网运行风险评估最大的不同在于其考虑的是调度操作对电网带来的影响， 因此调控操作风险应该对比操作前后风险， 基于此， 本研究将电网调控操作风险指标定义为操作前后系统运行风险指标的变化量， 提出考虑指数型操作人员实时综合因子的风险差分运算的电网调控操作的量化风险指标体系. 操作人员实时综合因子计及本次操作任务的强度、 时间段以及工作人员的状态. 该指标体系体现了电网调控操作的实质是系统运行状态的变化， 而非某一特定系统运行状态， 能够从本质上反映调控操作对电网产生的影响. 其计算方法为

其中：Rm和Rn分别对应系统操作前后风险；E指系统所有状态集合，E=C0∪C1∪{正常状态}，C0∩C1=∅，C0指筛选出的相应事故集，C1指其他类型事故集；P对应各事故发生的概率；Ib, x(x∈C0或C1)指断开C0或C1中第x条线路对应的后果；Ia, x(x∈C0或C1)指同时断开C0或C1中第x条线路和待操作目标线路的后果；Ib, n表示系统正常状态下的后果；Ia, n表示相应操作引起的后果；Ib和Ia分别指操作前后的事故后果；Kpe为人员风险综合因子.

其中：λ为操作文员操作前已工作小时数；S为本次操作任务强度；S=S1+0.8S2+1.2S3，S1、S2、S3分别对应操作票纯粹单项令、 综合令分解后的单项令及逐项分解后的单项令步骤数；Sav为同类型调度令的平均操作步数；t为本次操作所在的时间段取值0(6:00～18:59)、 0.5(19:00～23:59)、 1.0(00:00～05:59)；em表示人员心理状况： 取值为0.6(差)、 0.8(一般)、 1.0(好)， 一般取0.8.

分析中认为C1中的事故集对应的线路与待操作的目标线路之间的电气距离较远， 仅存在一定的弱耦合. 所以， 不影响断开C1中的线路与目标线路造成的后果， 故有下式

系统处于事故集C1的概率与其他状态的概率之和为1， 故有

则

算法在推导计算公式时考虑了完备事故集， 而且基于筛选出的重要事故集， 能够满足调控操作风险评估实时性要求， 且由于事故集的完备性， 故本算法风险指标的计算是精确的.

研究基于系统潮流过载以及节点电压越限等指标构建调度操作风险评估的指标体系.

当事故集C0中的故障c发生时， 第i条线路的潮流过载系数KS, ci和第j个节点的电压越限系数KV, cj分别由下式得到， 其示意图如图2、 3所示.

其中：Sci是第i条线路的实际功率；SN, i第i条线路的额定功率；Ucj是第j个节点的电压；Uinf, j和Usup, j是第j个节点允许电压的极值.

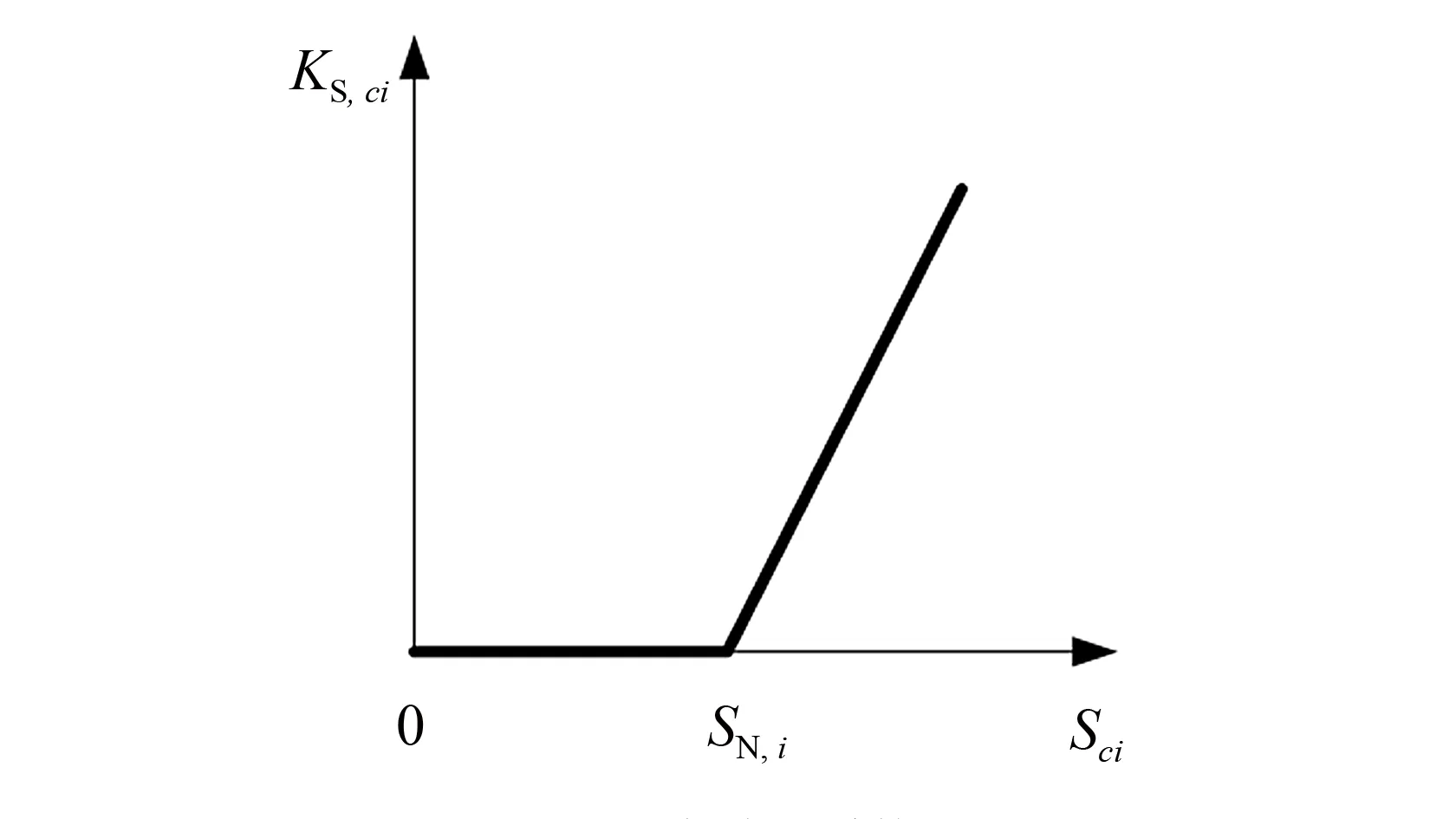
图2 潮流过载系数Fig.2 Power flow overload coefficient

图3 电压越限系数Fig.3 Voltage limit coefficient

线路过载状态IS, ci和节点电压越限状态IV, cj如下式所示， 其示意图如图4、 5所示.

IS, ci=eKS, ci-1，IV, cj=eKV, cj-1

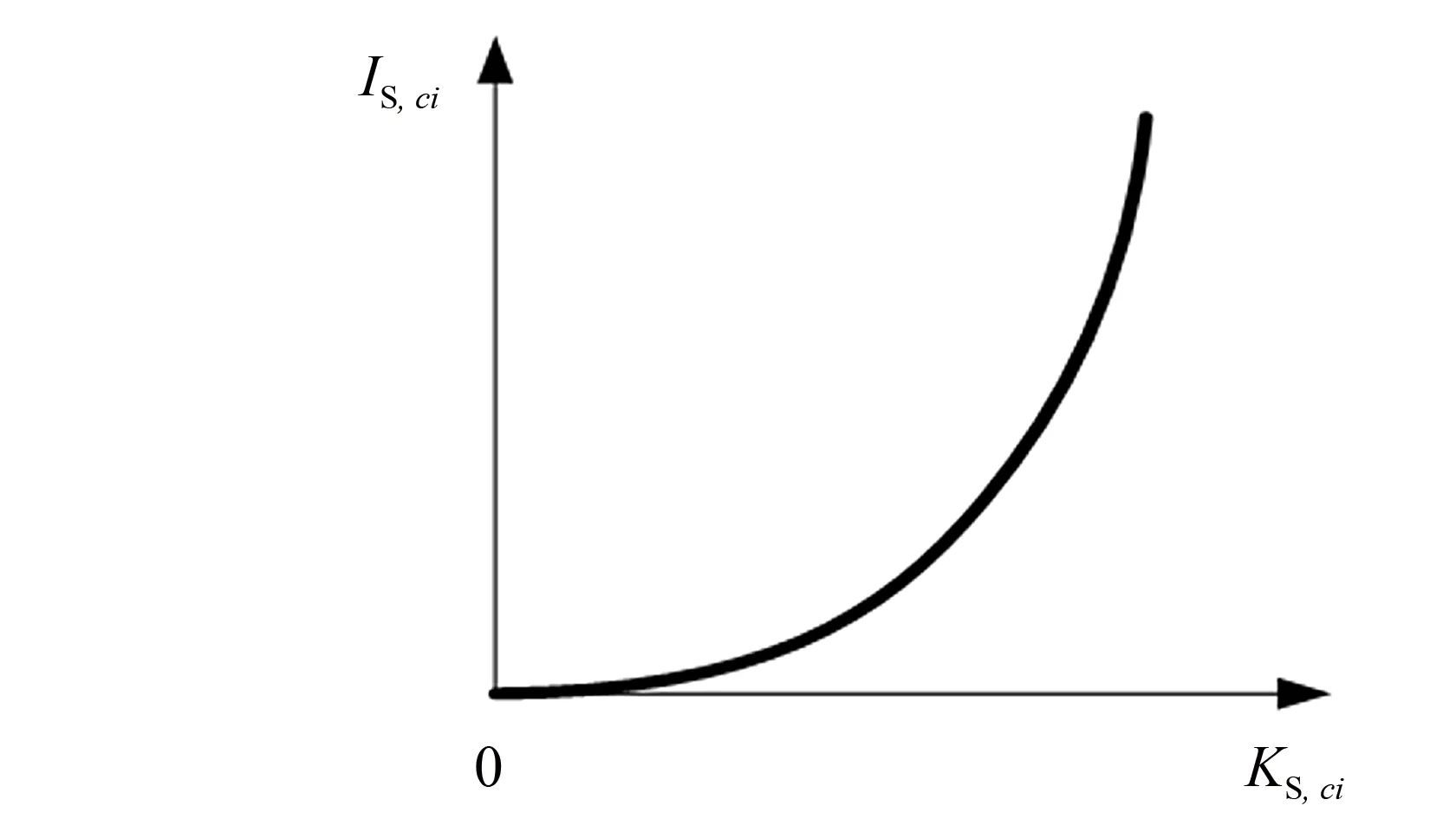
图4 潮流过载后果Fig.4 Consequence of overloading of power flow

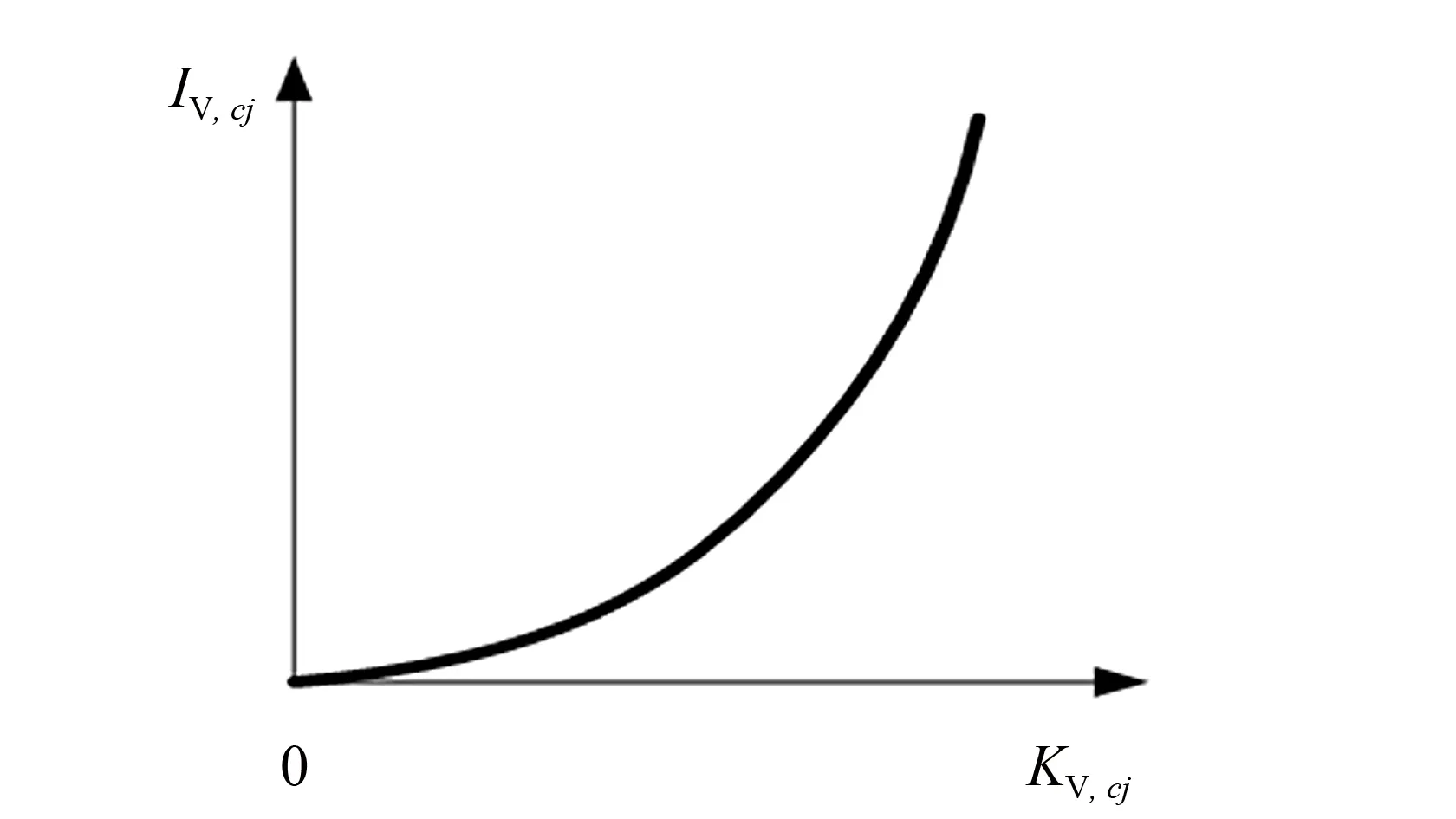
图5 电压越限后果Fig.5 Effect of voltage limit

第i条线路的过载风险评估值RS, ci和第j个节点电压越限的风险评估值RV, cj为

RS, ci=Pc·IS, ci，RV, cj=Pc·IV, cj

其中:Pc是事故c发生的概率.

故第i条线路过载的风险评估值RS, i和第j个节点电压越限的风险评估值RV, j为

其中:nc是事故集C0包含的事故数量.

通过对所有线路的潮流过载风险及所有节点的电压越限风险进行排序， 可以得到风险最大的线路和节点， 从而对其进行最有效的风险控制.

事故c引起的线路过载风险RS, c和第j个节点的电压越限风险RV, c为

其中:nl和nb分别表示系统线路和节点的数量.

通过对所有事故的潮流过载风险及所有节点的电压越限风险进行排序， 可以得到引起风险最大的事故， 从而对该事故进行最有效的风险控制.

系统线路过载和节点电压越限风险分别为

通过对系统的潮流过载风险及电压越限风险进行分析， 可以得出系统风险是否超出可接受风险范围， 从而决定是否执行该项操作.

3 调控操作的事故集筛选及实例分析

研究适用于调度操作的风险分析方法， 考虑到调控操作风险评估实际应用实时性的要求， 结合风险理论在电力系统中的应用， 建立可以满足准确性即能够为操作人员提供准确的风险水平信息以及保证快速性的风险评估的方法， 因为调度操作执行注重实时性， 若耗时过长， 将失去实际意义. 本算法基于调控操作对电网产生的影响， 生成风险评估所需事故集， 从而缩小事故集范围， 提高计算效率.

基于IEEE-118节点对事故集筛选法进行分析研究； 基于调控操作前后电网潮流的变化生成相应的事故集C0， 为电网运行风险评估提供依据. 包括以下两种核心方法.

1)基于局部潮流量化分析的调控操作关键影响设备搜索法.

第一步， 获取电网的实际运行数据和操作指令， 对操作前后的潮流进行对比分析； 第二步， 搜索调控操作关键影响设备. 首先， 判别操作前后的变化量ΔS与额定状态下SN比值绝对值超过δS的线路为调控操作主要影响线路， 即

式中： ΔS是操作前后的变化值;SN是线路额定值；δS为阈值. 然后， 判别操作前后电压的变化量ΔV(p.u.)超过δV的节点为调控操作主要影响节点， 即

ΔV>δV

式中： ΔV是操作前后节点电压的变化量；δV为阈值.

以IEEE-118节点为例进行说明， 其网络结构如图6所示. 两个方案操作的线路分别为8-5、 30-17线路， 相应的基于指数型操作人员实时综合因子差分运算风险评估的参数分别为δS=0.2和δV=2×10-2p.u.， 假定操作两条线路的时间都为20:00， 对应λ为2 h，t取0.5， 操作由一个单项令和一个综合令组成， 其中综合令可分解成6个单项令， 所以S取5.8，Sav取5，em取0.8.

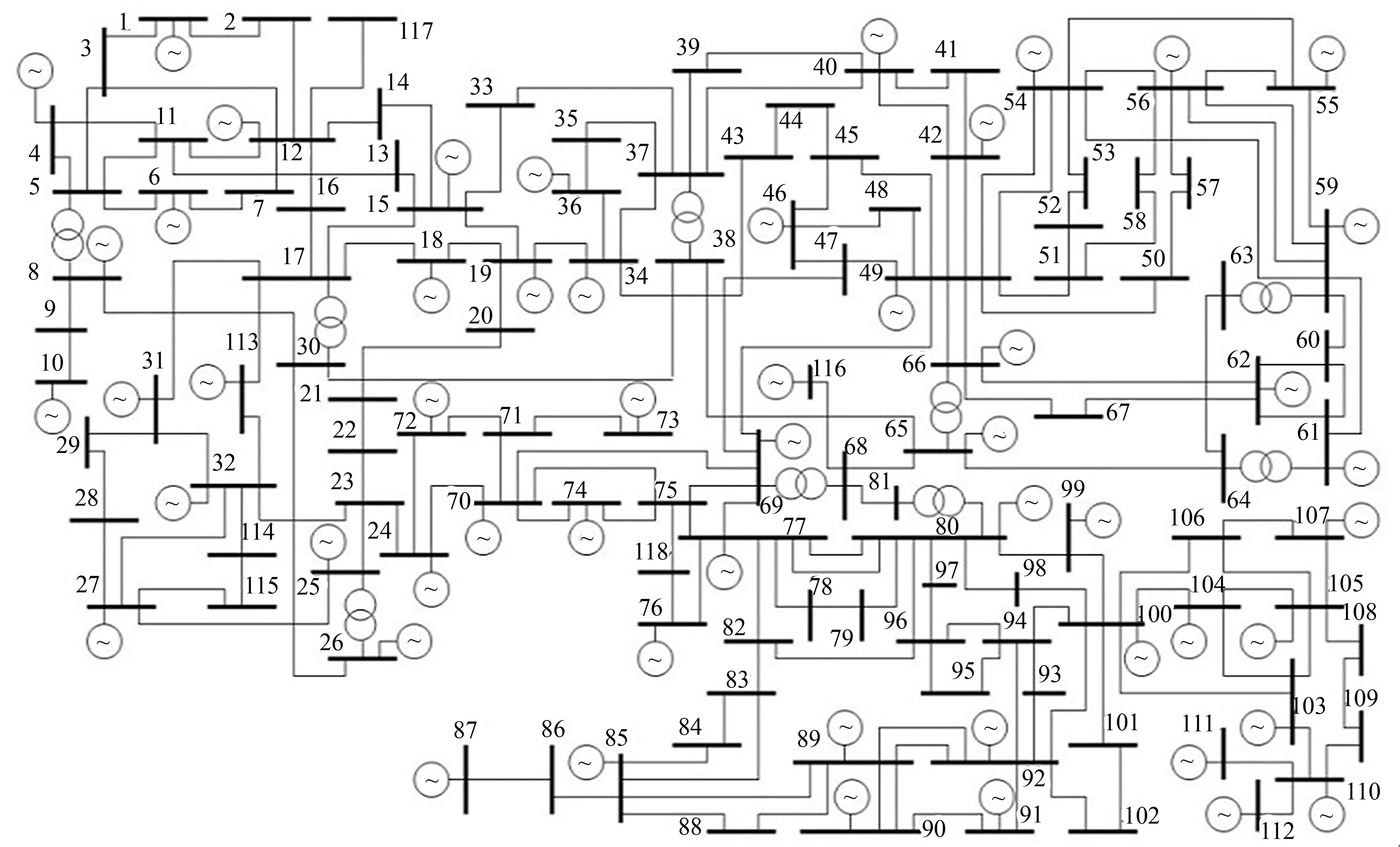
图6 IEEE-118节点系统拓扑结构Fig.6 IEEE-118 node system topology

线路8-5、 30-17操作前后系统的潮流分布情况分别如表1、 2所示. 操作线路8-5时， 线路7-12、 5-6、 12-14、 13-15、 30-17、 15-17、 14-15、 12-16及8-30为关键线路； 操作线路30-17时， 线路12-14、 7-12、 19-20、 16-12、 17-18、 16-17、 18-19、 30-20及30-21为关键线路. 两种方案情况下节点16的ΔV分别为1.951 8×10-2、 2.018 7×10-2p.u.， 都是越限的关键节点， 线路7-12、 12-14、 12-16、 16-17在两个操作方案里都是越限的关键线路， 需要关注.

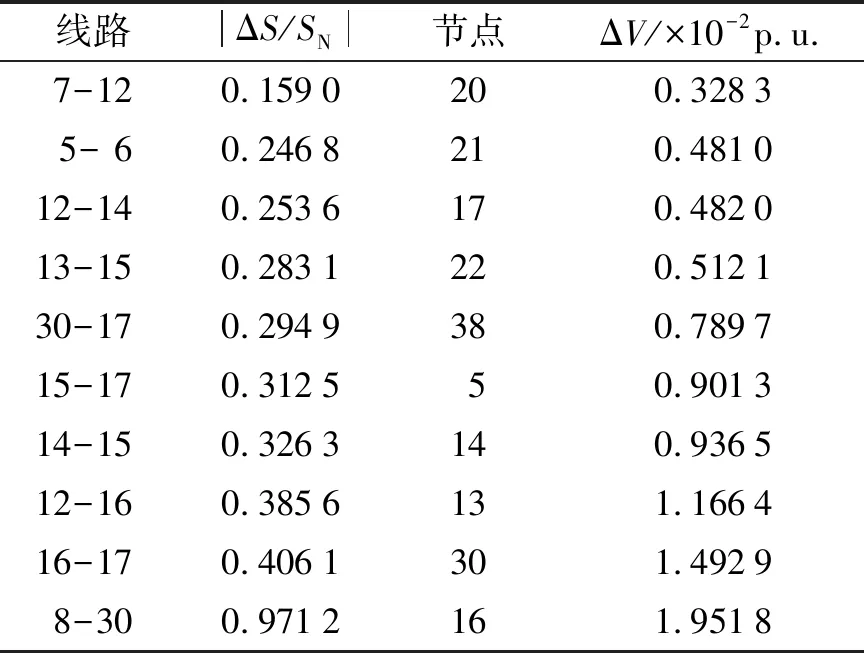
表1 操作线路8-5的ΔS/SN以及节点的 ΔV排序

表2 操作30-17线路的ΔS/SN以及节点的 ΔV排序

2) 基于局部拓扑相关性分析的调控操作重要事故集筛选法.

基于局部拓扑相关性分析的调控操作重要事故集筛选法以广度优先搜索为基础， 广度优先搜索具有搜索与搜索中心关联性最紧密元件的优势[13]. Dijkstra单源最短路径算法和Prim最小生成树算法都融合了宽度优先搜索的思想， 目的是全面展开并搜索所有的节点， 以找到结果.

接下来仍以IEEE-118节点为例进行说明， 在基于深度优先搜索方法对操作8-5线路搜得关键线路和关键节点后， 进行广度搜索， 搜索的深度N为1， 得到相应的事故集如图7所示. 为了更好地说明本研究方法的有效性， 设δS=0.3；δV=2×10-2p.u., 得出相应的风险指标误差和计算时间分布情况如图8所示.

从图8可知, 事故数量N增大时， 相应的计算误差随之减小， 计算误差越小越能反映本文所提方法能够提高找出调度操作敏感元件的准确性， 故所筛选的事故集C0可以满足调度操作风险评估的精度要求.

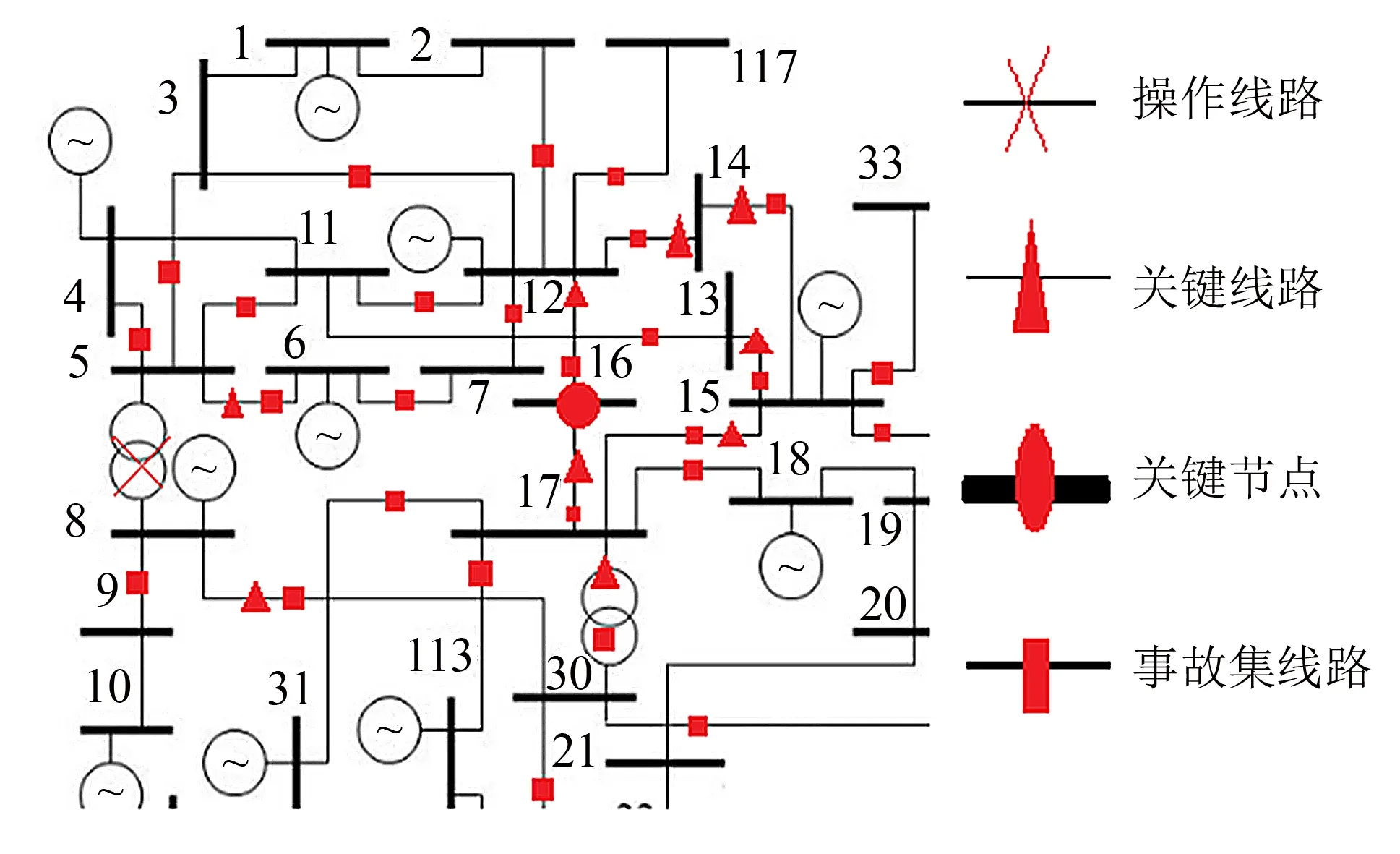
图7 关键设备以及事故集Fig.7 Key equipment and accident set

图8 计算时间及风险指标误差Fig.8 Calculation of time and risk error

针对操作线路8-5的情况， 对N=1时的风险进行分析. 各事故节点电压越限指标排序如表3所示. 由表3可知， 产生ΔRV的主要原因在于关键断面的几条事故线路如12-14、 12-16、 13-15、 30-17、 14-15以及16-17. 如表4所示， 节点13、 16的ΔRV占系统ΔRV的66.92%， 线路8-30的ΔRS占系统ΔRS的99.82%， 断开8-5线路的操作使潮流经过节点13、 16转移， 从而降低其实际电压.

操作8-5线路时， 可采取如下调节手段对防控效果和调控手段进行平衡： ① 增加1、 4、 6、 12号发电机出力60 MW， 降低10号发电机出力240 MW； ② 启用8-30线路的备用线路； ③ 对节点12、 16、 117进行无功功率补偿， 补偿度为90%， 各种方案的风险防控结果如图9所示. 操作30-17线路时， 可采取如下措施： ① 增加1、 4、 6、 12号发电机出力60 MW， 降低10号发电机出力240 MW； ② 启用21-30线路的备用线路； ③ 对节点12、 16、 117进行无功功率补偿， 补偿度为90%， 各种方案的风险防控结果如图10所示.

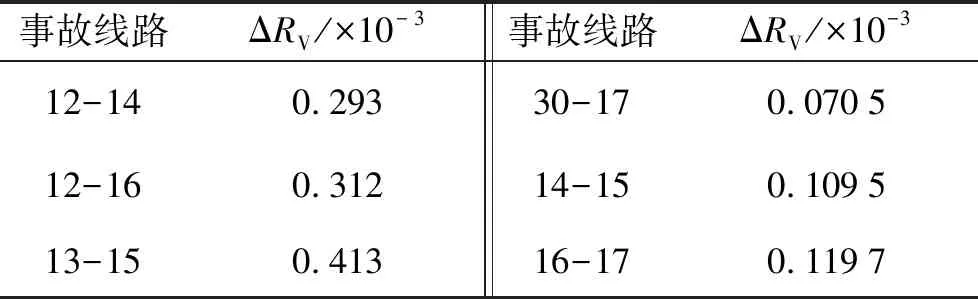
表3 各事故节点电压越限指标排序

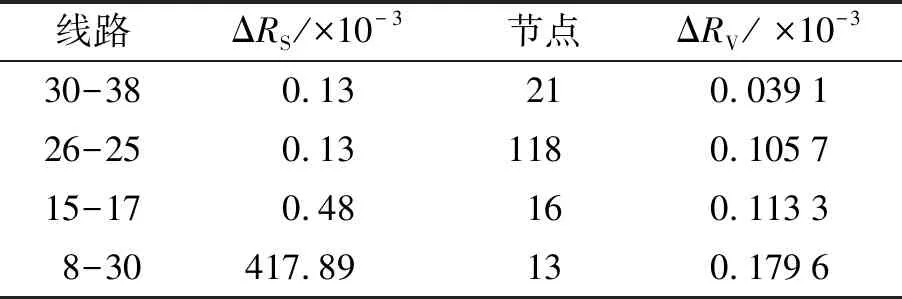
表4 ΔRS和ΔRV排序

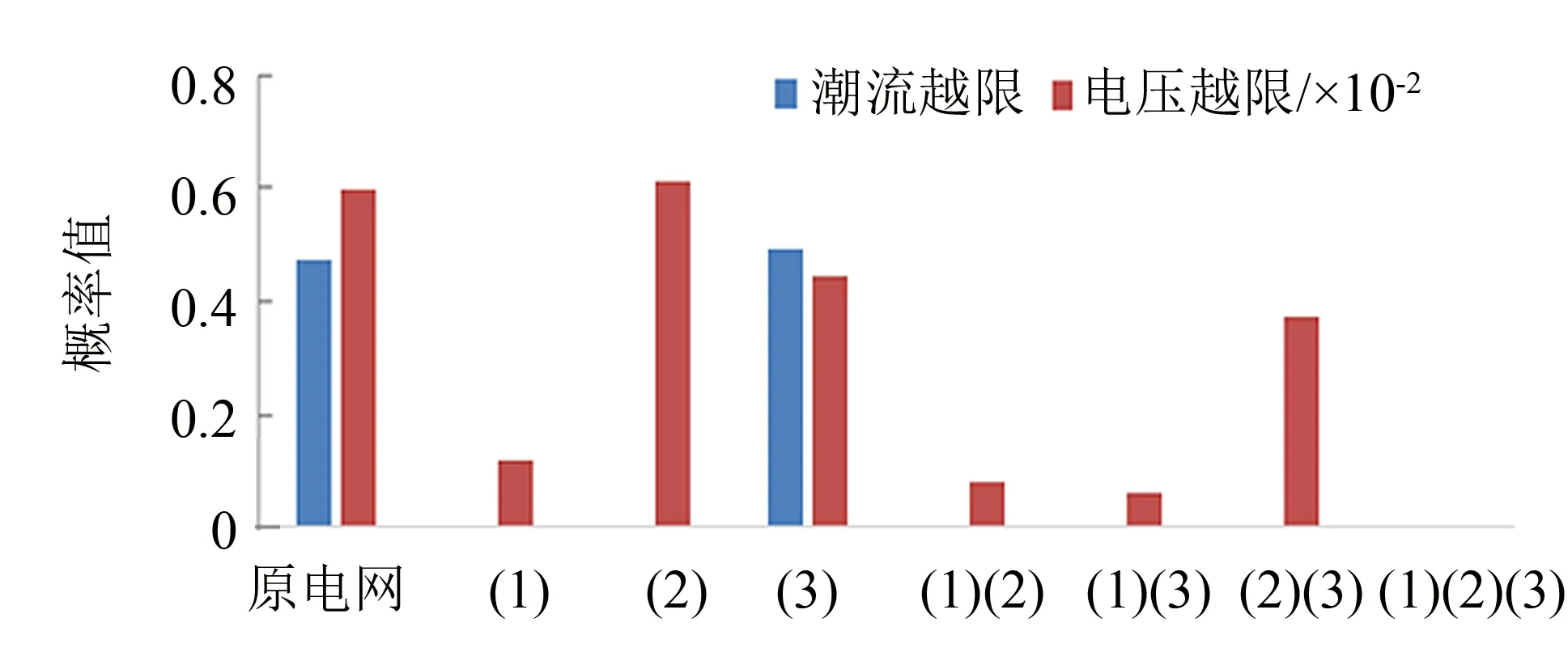
图9 操作线路8-5各调节方案的风险防控效果Fig.9 Risk prevention and control effect of line 8-5 operation

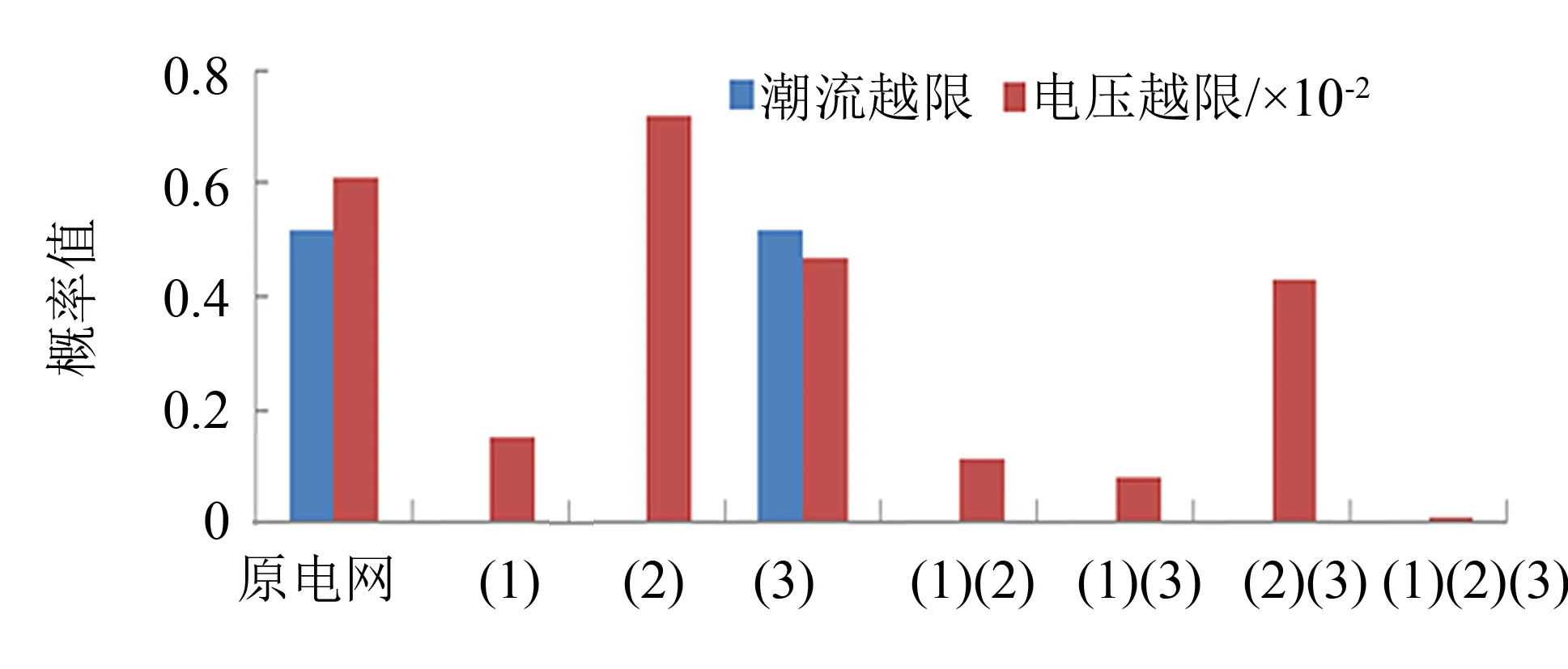
图10 操作线路30-17各调节的风险防控效果Fig.10 Risk prevention and control effect of line 30-17 operation

4 结语

电网调控操作风险评估， 主要是为了及时发现电网运行中的异常状态， 以便于及时得到检修， 从而能够将损失降到最低. 本研究提出并建立考虑指数型操作人员实时综合因子风险差分算法的电网调控操作风险快速评估体系， 实现调控操作风险指标的快速分析， 解决传统风险指标体系无法反映电网运行风险动态变化过程的问题. 通过案例证明所提方法的有效性， 为调控操作人员提供反映目标操作指令对电网风险影响的量化指标， 便于调控操作人员及时判断目标操作对电网运行风险的影响， 进而制定降低操作风险的针对性措施， 为调度人员调度决策工作提供方便， 具有重要的现实意义.