弧底梯形混凝土衬砌渠道冻胀破坏力学模型研究

赵晓磊，王红雨

(宁夏大学 土木与水利工程学院，银川 750021)

宁夏引黄灌区是全国古老的大型灌区之一。随着灌区农业用水的增加，为了减少渗漏损失，提高渠道输水能力，自20世纪70至80年代起，开始对渠道进行防渗衬砌。但由于宁夏地处季节性冻土区，冬季气温低，历时时间长，渠道衬砌工程因冻胀引起的破坏较为严重，特别是地下水位较高的地区更为显著，导致工程效益低，维修费用加大等一系列问题。

许多学者基于土体冻结过程和冻结原理的研究，对土体水热力的耦合进行了模拟[1-2]。但这种方法过于复杂，作为寒区结构冻胀效应的预测性工具不太方便。从土与结构相互作用的角度研究结构的冻胀效应，建立量化、通用的渠道冻胀破坏力学模型得到学者的广泛关注[3-4]。其中，弧底梯形渠道以其良好的抗冻胀性能和水利特性在北方寒旱地区得到广泛应用。王正中、李甲林(2008)通过对弧底梯形渠道冻胀破坏机理和破坏特征的分析，指出渠道整体计算简图是在法向冻胀力、切向冻结力和重力共同作用下的薄壳拱形结构，并通过适当假设建立了弧底梯形渠道混凝土衬砌结构的冻胀破坏力学模型[5]；孙杲辰、王正中(2012)考虑地下水位较高时渠道衬砌各部位的受力特征，通过整体平衡计算法确定渠坡板法向冻结力的位置，建立了高地下水位弧底梯形混凝土衬砌渠道冻胀破坏力学模型[6]；郑源(2015)考虑复合土工膜与土壤间的摩擦力，将渠坡板视为在冻结力、冻胀力和摩擦力作用下的悬臂梁，并建立了进一步的模型[7]。但是上述研究均未考虑渠道冻胀破坏过程中法向冻结力的分布情况，且计算得到的法向冻结力为作用在渠坡板的集中力，而渠底板法向冻结力仍为未知力。因此，本文在总结前人成果的基础上，将法向冻结力分布形式考虑在内，分析应变率、温度等因素对冻结黄土抗拉强度的影响，并考虑到坡板与底板整体性强的特点，建立高地下水位弧底梯形混凝土衬砌渠道的冻胀破坏力学模型，以期能为宁夏引黄灌区弧底梯形衬砌渠道的抗冻胀研究提供参考。

1 弧底梯形渠道的冻胀破坏特征

弧底梯形渠道是一种水利条件接近于U形渠道的断面形式，它具有湿周短、流速快、输水能力大、水量损失小等特点。除此之外，其底部设计为反拱形结构，整体性强，受力条件好，在土壤冻胀力作用下，由于其整体承重及反拱能力，减轻了冻胀破坏及衬砌板裂缝产生的几率，提高了防渗工程的耐久性。弧底梯形渠道渠底板受两端坡板约束，冻胀变形呈中部大、两端小，且整体有上抬趋势，通常在渠底中部容易发生冻胀破坏。但与梯形渠道相比，所受法向冻胀力有所减小，发生冻胀破坏的可能性较梯形渠道亦有所减小。渠坡板顶部所受冻结力和法向冻胀力较小，下部受渠底板约束，所受法向冻胀力较大，随冻胀加剧，冻结力和法向冻胀力增大，使渠坡板产生较大内力，容易在坡板下部产生冻胀裂缝。这也是渠道产生冻胀破坏的关键原因，因此冻结力的分布对渠道冻胀破坏的影响显著。

2 弧底梯形渠道法向冻结力的分布规律

建筑物基础埋入冻土中，通过冰晶将土颗粒同基础胶结在一起，这种胶结力称为土与基础间的冻结强度，简称冻结力[8]。冻土的含水量达到土体饱和含水量，冰晶体几乎充填了土的孔隙，最大可能将土粒胶结，此时的含水量叫做冻结强度的极限含水量。含水量继续增大，原孔隙水和未冻区迁移水分冻结体积膨胀不仅填满土体中全部孔隙，而且使土颗粒发生相对位移，即冻胀。在渠道发生冻胀期间，被约束冻胀的土体产生垂直作用在衬砌板底面的法向冻胀力。当渠道处于极限平衡状态时，法向冻胀力达到冻结强度的最大值，随着温度、含水量等因素的进一步变化，当法向冻胀力大于冻土的抗拉强度时，渠道在垂直于衬砌板方向产生冻胀位移。而冻土的抗拉强度与应变率、温度、含水量和破坏时间有关，以宁夏典型湿陷性黄土为例，分析如下：

1) 研究表明，当应变率在10-6～10-3s-1较低范围内时，饱和冻土的抗拉强度与应变率呈线性关系，并且变化速率随温度的降低而增大。根据《水工建筑物抗冰冻设计规范》(GB50662-2011-T)表8.2.1，弧底梯形混凝土衬砌渠道允许法向位移值为10～30 mm，而宁夏引黄灌区冬季气温低，历时时间长，在一个完整冻融周期内渠道应变率变化范围为1.29×10-5～3.87×10-5s-1，满足冻土抗拉强度与应变率呈线性关系的条件。

2)饱和冻土在低应变速率下，抗拉强度随温度降低呈线性增大趋势；在高应变速率下，增大趋势在-5℃以上温度时加快，低于-5℃时降低。试验资料表明，在高于-5℃时，未冻含水量随冻土区温度降低而急剧较少，使温度对冻土抗拉强度的影响更为显著；在低于-5℃时，未冻水随温度进一步降低而逐渐趋于稳定，同时在较大应力作用下，冰基质变形生成热，导致冻土中未冻含水量的增加。而宁夏引黄灌区弧底梯形混凝土衬砌渠道基土冻胀应变率较低，渠道同一时间，相同层地温值由渠顶至渠底依次降低[9]，满足冻土在低应变速率下，抗拉强度与温度呈线性关系的条件。

3)渠道未发生冻胀破坏时，可不必考虑破坏时间对冻土抗拉强度的影响。

综上所述，弧底梯形渠道渠坡板法向冻结力从渠顶至坡脚处呈线性增大分布。渠底板因受两端坡板约束，法向冻结力呈均匀分布。

3 弧底梯形衬砌渠道力学模型的建立

3.1 基本假定

1)假定冻土和混凝土均为线弹性材料，则不同荷载引起的作用效果和各向形变都在弹性范围内，即可以应用叠加原理。

2)渠道坡板在坡脚处与渠底板相互约束，渠道整体性较强，渠顶呈自由变形，将渠道坡板视为悬臂梁，忽略衬砌板与渠基土间的摩擦力和渠基土对衬砌板的支持力。

3)冻胀量沿渠底板呈均匀分布，沿渠坡板呈线性分布，渠顶为零，于坡脚达到最大值。法向冻胀力分布规律与冻胀量相同，也沿渠底板呈均匀分布，沿渠坡板呈线性分布，渠顶为零，于坡脚达到最大值。

4)渠基土固结已全部完成，不考虑未冻土的压缩效应。

5)渠道坡板法向冻结力从渠顶至坡脚处呈线性增大分布。渠底板受两端坡板约束，法向冻结力呈均匀分布。

6)冻土弹性模量远小于混凝土弹性模量，即冻土不参与衬砌板的弯曲变形，只对混凝土衬砌板施加冻胀力，并提供被动冻结约束。

7)弧底梯形混凝土衬砌渠道可简化为由法向冻结力提供约束，在对称分布的重力、法向冻胀力和切向冻结力作用下，保持静力平衡的薄壳拱形结构。

3.2 渠道断面及受力图

弧底梯形渠道结构断面示意图见图1。其中，渠坡板长为L，弧底中心角为2α，衬砌板厚度为b，弧底半径为R，渠坡顶端设为A点，坡脚处为B点，弧底中心线处为C点。

图1 弧底梯形渠道衬砌结构断面示意图

极限平衡状态时，弧底梯形渠道法向冻胀力分布见图2，并设B点最大法向冻胀力为q。

图2 法向冻胀力分布

弧底梯形渠道切向冻结力分布见图3，并设B点最大切向冻结力为τ。

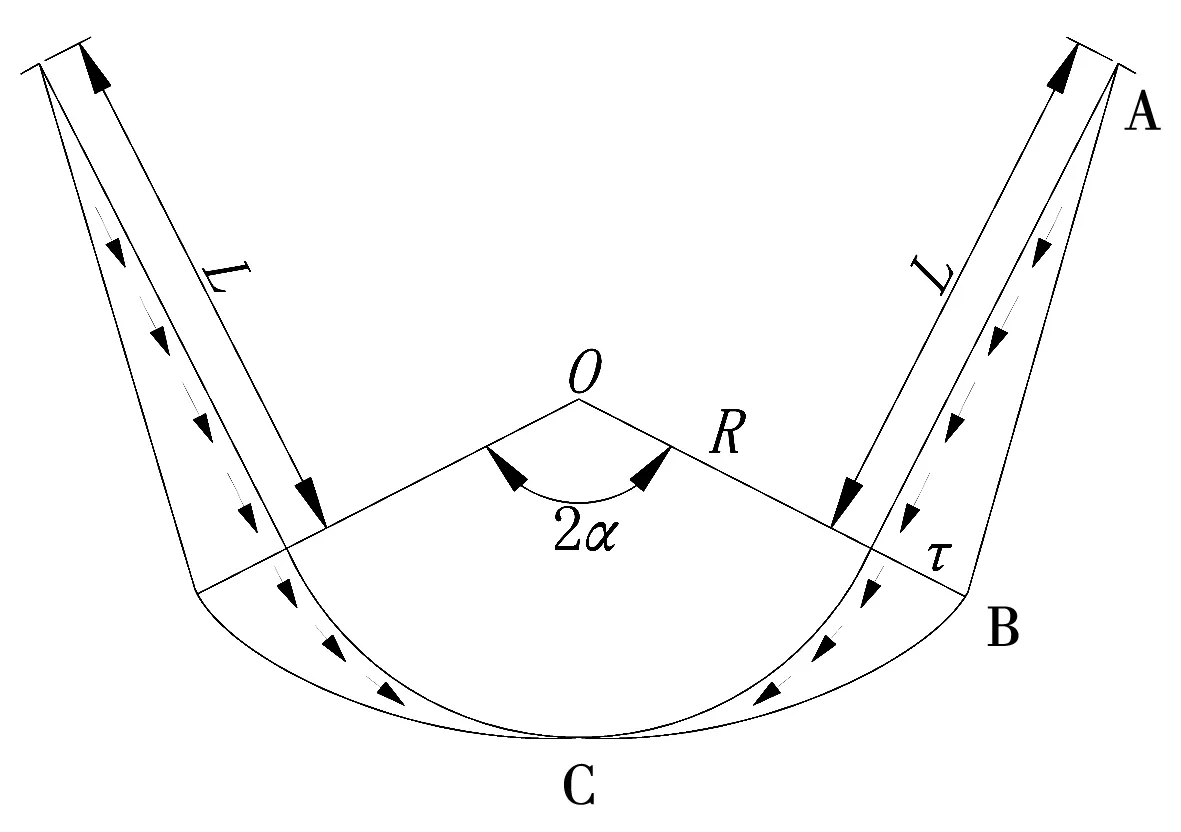
图3 切向冻结力分布

极限平衡状态时，弧底梯形渠道法向冻结力见图4，并设B点最大法向冻结力为F。

图4 法向冻结力分布

渠道达到极限冻胀平衡状态时，渠坡板与基土间切向冻结力在坡脚处达到最大值，其值与土质、温度和含水量等因素有关，可根据渠道具体情况确定，属已知力。渠道受力图中只有最大法向冻胀力q和最大法向冻结力F为未知力。

根据渠道整体在竖直方向的平衡条件，即由∑Y=0得：

(1)

根据渠道整体在水平方向的平衡条件，即由∑X=0得：

(2)

联立以上两个方程，即可得渠道在极限冻胀平衡状态下的最大法向冻胀力和最大法向冻结力表达式分别为：

(3)

(4)

将式(4)代入式(3)可得：

(5)

4 力学模型求解

4.1 渠道坡板内力

以渠顶A点为坐标原点，建立直角坐标系见图5。其中，法向冻结力、法向冻胀力和重力沿坡板线性分布，切向冻结力沿坡长线性分布，M、Q、N为渠底板对坡板的弯矩、剪力和轴力。将渠坡板视为在以上力作用下的悬臂梁，计算简图如下。

图5 渠坡板计算简图

渠坡板支座反力计算如下(假设RBy方向向下，RBx方向向左)：

(6)

(7)

渠坡板内力计算如下：

假定x为从坡顶起的坡板长度，则x∈(0，L)，任意截面弯矩计算式如下：

(8)

任意截面轴力计算式如下：

(9)

任意截面剪力计算式如下：

(10)

渠坡板内力分布见图6。图6表明，弧底梯形渠道渠坡板轴力在坡脚处达到最大值，以受压为主；最大弯矩值在坡脚处，以坡板内侧受压、外侧受拉为主；渠坡板剪力在坡脚处达到最大值，以围绕截面体有逆时针转动趋势为主。渠坡板的内力计算中，规定轴力方向为拉正压负；弯矩方向为使截面体产生下凸变形为正，反之为负；剪力方向为使微段产生左端向上，右端向下错动为正，反之为负。

图6 渠坡板内力图

4.2 渠道底板内力

以渠底C点为坐标原点，建立直角坐标系见图7。

图7 渠底板计算简图

其中，任意截面距渠底中心线角度用θ表示；MB、QB、NB为渠坡板对渠底板的弯矩、剪力和轴力；Mθ、Qθ、Nθ为求解截面弯矩、剪力和轴力。根据渠底板的计算简图，由∑X=0可得任意截面处的轴力计算式为：

Nθ=NBcos(α-θ)+QBsin(α-θ)+

(11)

由∑M=0可得任意截面处弯矩计算式为：

Mθ=QBRsin(α-θ)-MB-NB[R-Rcos(α-θ)]+

(12)

由∑Y=0可得任意截面处剪力计算式为：

Qθ=NBsin(α-θ)-QBcos(α-θ)-

(13)

渠底板内力分布见图8。图8表明，弧底梯形渠道的控制内力在坡脚和弧底位置。渠底板轴力在弧形底部达到最大值，主要以自重和切向冻结力产生的压力为主，法向冻胀力对轴力的影响较小；渠底板弯矩在弧形顶部达到最大值，主要以自重和切向冻结力产生的负弯矩为主，使渠道内侧受拉，体现了弧形底板的反拱作用；渠底板剪力在弧形顶部达到最大值，主要以法向冻结力、自重和切向冻结力产生的负剪应力为主。图8中规定轴力方向为拉正压负；弯矩方向为使截面体产生下凸变形为正，反之为负；剪力方向为使微段产生左端向上，右端向下错动为正，反之为负。

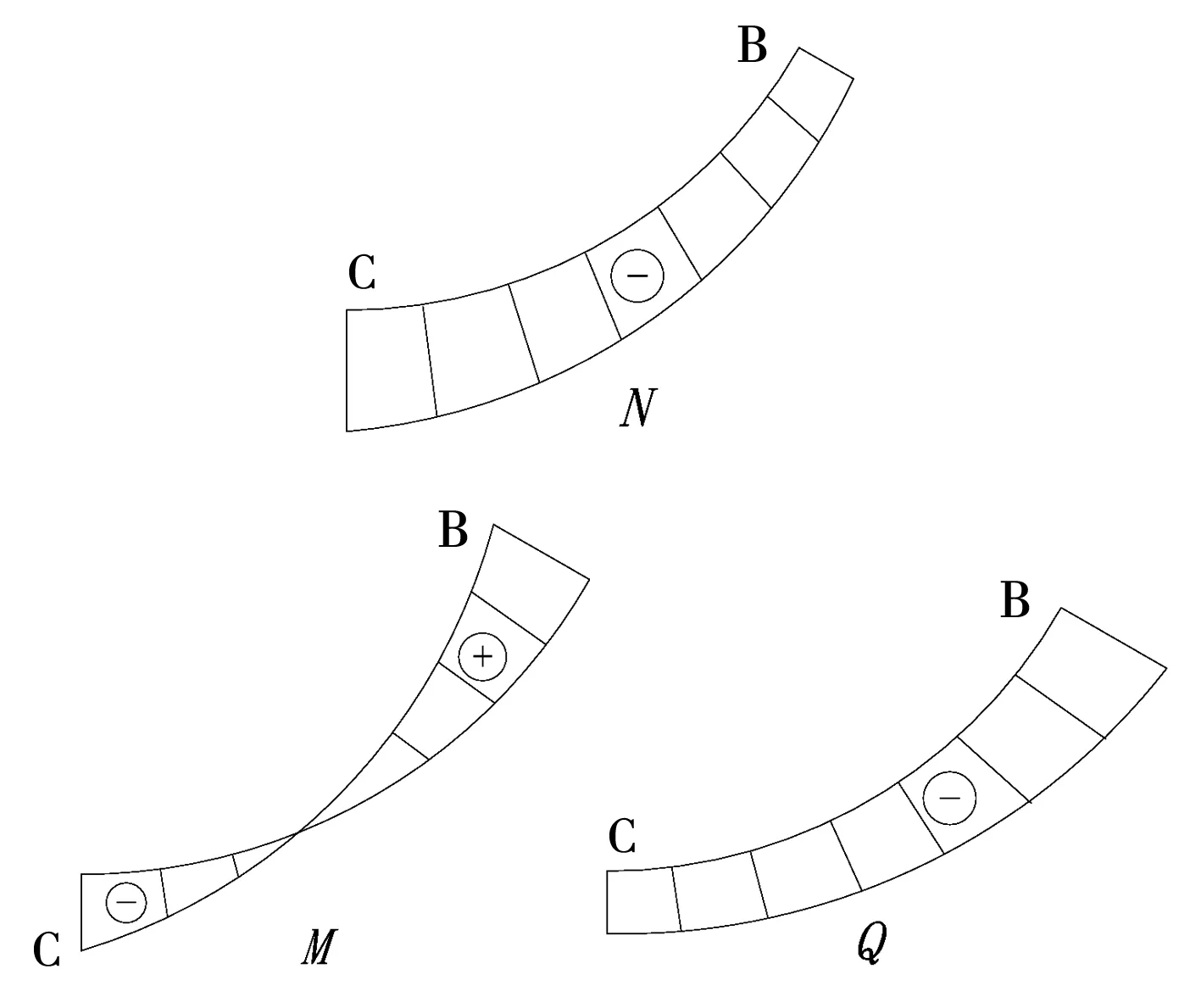
图8 渠底板内力图

4.3 混凝土渠道衬砌板厚度及抗裂验算

弧底梯形渠道的渠坡板和渠底板都可简化为压弯构件，衬砌结构在最大弯矩处的最大拉力及最大拉应变决定渠道是否发生胀裂，此过程一般不考虑剪力的影响，方法如下：

渠坡板最大弯矩处的拉应力最大，计算式如下：

(14)

渠底板最大弯矩处的拉应力最大，计算式如下：

(15)

渠道最大拉应变及抗裂条件计算式如下：

(16)

式中：EC为混凝土的极限拉应变；εt为混凝土的弹性模量。

5 应用实例

已知某弧底梯形渠道，预制砼强度标号为C15，衬砌板厚b=0.07 m，弧底半径R=0.7 m，渠坡板长L=1.4 m，材料密度ρ=2 400 kg/m3，坡脚α=45°，C15砼混凝土极限拉应变εt=0.5×10-4，弹性模量EC=2.2×104MPa。阴阳坡冻土层温度分别为-15℃和-12℃。具体计算如下：

5.1 最大切向冻结力计算

最大切向冻结力可按以下经验公式计算：

τ=c+mt

(17)

式中：t为负温的绝对值；c、m分别为与土质有关的系数，c=0.3～0.6，kPa；m=0.4～1.5，kPa/℃。本例中取c=0.4 kPa，m=0.6 kPa/℃，t=15℃。

由式(17)计算得：

τmax=9.4 kPa

5.2 最大法向冻胀力计算

由式(4)计算得：

Fmax=18.13 kPa

由式(5)计算得：

qmax=8.23 kPa

5.3 渠坡板内力计算

由式(8)计算得：

MB=4.63 kN·m

由式(9)计算得：

NB=-8.25 kN

由式(10)计算得：

QB=-8.6 kN

5.4 渠底板内力计算

当θ=0°时，由式(11)计算得：

N0=-12.28 kN

由式(12)计算得：

M0=-0.9 kN·m

由式(13)计算得：

Q0=-6.84 kN

5.5 衬砌板厚度及抗裂验算

混凝土极限拉应力σt=Ecεt=1.1 MPa，渠坡板最大弯矩处拉应力由式(14)计算得σmax=5.55 MPa>σt，所以渠坡板有可能发生冻胀破坏。

渠底板最大弯矩处拉应力由式(15)计算得σmax=1 MPa<σt，所以渠底板不会发生冻胀破坏。

6 计算结果分析

计算结果表明，渠坡板最大弯矩产生在坡脚位置，衬砌板外侧受拉，坡板以受剪为主。其中，自重和法向冻结力均布加载在不均匀冻胀土上，产生不利用衬砌平衡的剪应力，同时使危险断面弯矩增大，导致裂缝产生。

渠底板以受轴向压力为主，所受弯矩较小，减轻了渠底板冻胀破坏。实例计算表明，渠底板最大法向冻结力大于最大法向冻胀力，且受两端坡板的约束，不易产生冻胀破坏。

7 结 论

1) 弧底梯形渠道未发生冻胀破坏时，在各因素影响下渠坡板法向冻结力从渠顶至坡脚处呈线性增大分布，渠底板受两端坡板约束，法向冻结力呈均匀分布。

2) 在考虑法向冻结力分布情况下建立的力学模型，会导致渠道最大受力发生变化。其中，最大法向冻结力计算公式同时适用于渠坡板和渠底板，相比于将法向冻结力视为作用在渠顶的集中力，更加符合实际情况。本文选取的参变量，即切向冻结力的取值，还有待进一步的研究。

3) 当地下水可以补给到渠顶时，渠坡板以自重和法向冻结力产生的剪应力为主，随冻胀加剧，法向冻结力增大，同时使危险断面所受弯矩值增大，从而促使衬砌板产生裂缝。渠底板以受轴向压力为主，主要由自重和切向冻结力产生。

4) 本文以宁夏引黄灌区的季节性冻土条件和各因素为基础，分析了渠道法向冻结力的分布规律，建立了弧底梯形混凝土衬砌渠道的冻胀破坏力学模型，为宁夏地区渠道抗冻胀破坏设计提供依据和参考。