小样本下装备平均修复时间的非统计估计模型
2019-05-23柯宏发祝冀鲁孙云辉
柯宏发, 祝冀鲁, 孙云辉
(1. 航天工程大学航天保障系, 北京102206; 2. 北京亚美联技术有限公司, 北京100080)
武器装备维修性是指装备在规定的条件下和规定的时间内,按规定的程序和方法进行维修时保持或恢复其规定状态的能力[1]。对装备维修性进行计算、验证和评估[2],通常必须选用一系列定性和定量的维修性参数[3]。由于装备平均修复时间直接影响装备的可用性、战备完好性,且与维修保障费用有关,因此成为描述装备维修性的一个主要参数。
目前,对装备平均修复时间进行估计与验证的常用方法为:在自然故障或模拟故障条件下进行试验,根据试验数据分析判定维修性是否达到标准要求。这种验证方法的理论基础是经典数理统计学,需要假设样本的概率分布特征,且需要较大的样本量才能得到较高的估计精度。针对小样本处理的Bayes方法[4-6]属于一种概率统计方法,需要利用验前信息并确定其概率分布形式,且非常依赖于验前信息的融合正确性[7]。然而,随着武器装备的复杂化、网络化、体系化发展,获取较多装备维修性验证试验样本量的难度越来越大,成本也越来越高,亟需解决未知概率分布前提下小样本数据的扩展生成、参数估计等技术难题。
在未知概率分布前提下,小样本数据处理通常基于以下2种模式:1)基于不确定理论相关方法的直接估计方法[8],但这种方法难以给出参数估计的置信度;2)基于GM(1,1)模型等不确定理论相关方法的间接估计方法[9-13],如灰自助生成方法。均值GM(1,1)模型具有一定的适用范围,对非指数增长或振荡数据序列的均值GM(1,1)模型拟合误差偏大,而装备维修时间虚拟样本原始数据序列往往呈现振荡特征。对于非指数增长或振荡数据序列,应优先选择离散形态的原始差分、均值差分或离散GM(1,1)模型[14-15]。
笔者借鉴灰自助的样本生成思想[10-13],提出通过离散GM(1,1)模型产生虚拟总体样本的新方法,并通过未确知有理数[16-17]对总体样本进行相应的点估计和区间估计,最后对算例进行了对比验证。
1 小样本数据的离散GM(1,1)模型生成
在武器装备试验活动中,由于试验条件和费用的限制,很多测试指标得到的数据样本量很小,其数据集合可以描述为
T′={x(t′),t′=1,2,…,N},
(1)
式中:x(t′)为第t′个测量数据;N为测量数据总数,通常情况下N∈[5,10]。对于此类小样本指标数据,难以确定其概率分布特征,即使假设其服从正态分布,其参数估计的置信度也难以保证。灰色系统理论认为:这N个小样本数据所携带的信息不足以确定测试指标的真实状态和数量关系,但已经部分地反映了测试指标的真实状态。通过“已知部分”推断“未知部分”正是灰色系统技术与方法的优势。
1.1 离散GM(1,1)模型
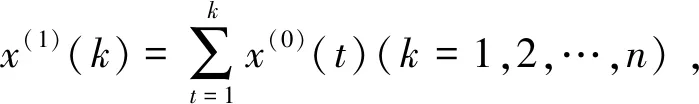
x(1)(k+1)=β1x(1)(k)+β2
(2)
为GM(1,1)模型的离散形式,简称离散GM(1,1)模型。式中:β1,β2均为待估计参数。
由最小二乘法(β1,β2)T=(BTB)-1BTY,得到β1、β2的值。由
(3)
(4)
并结合初始条件x(1)(0)=x(0)(1),即可得到离散GM(1,1)模型的时间响应序列
(5)
再将式(5)累减还原,得到X(0)的预测模型为
k=1,2,…,n。
(6)
在装备维修时间的实际建模过程中,可以取初始序列为X(1),对其一阶累减生成序列X(0)建立离散GM(1,1)模型,从而直接对X(1)进行模拟。
1.2 基于离散GM(1,1)模型的自助抽样生成
根据GJB2072—94《维修性试验与评定》[2]规定:维修作业样本量按选取的试验方法中的统计计算确定,也可选择推荐样本量。在此,将自助抽样生成的样本量选为推荐样本量,即N+A=30。
自助抽样生成原理的基本思路为:从原始数据集合X中等概率可放回地随机抽取1个数据,记为x1(1),该抽取过程重复m次,得到第1个自助样本,记为
X1={x1(1),x1(2),…,x1(m)}。
(7)
根据离散GM(1,1)模型的建模数据需求,确定m=5~8。为获得自助样本,将整体抽取过程连续重复A次,则会得到A个自助样本,可记为
YA={X1,X2,…,Xi,…,XA},
(8)
式中:Xi={xi(1),xi(2),…,xi(m)}。
针对自助样本Xi建立离散GM(1,1)模型,对其时间响应序列进行一次累减生成,即可得到自助样本Xi中第m+1个预测值,记为
(9)
进而得到自助样本集合,即新的装备维修时间数据集合,为
X′={x(1),x(2),…,x(N),…,x(N+A)}。
(10)
式中:x(N+1),x(N+2),…,x(N+A)分别为A个自助样本的离散GM(1,1)模型预测值。
上述自助抽样生成流程如图1所示。基于离散GM(1,1)模型的自助抽样生成,是通过对原始数据序列的随机抽样挖掘,拟合生成了符合参数估计要求的数据信息,而未对原始数据序列的概率分布信息进行假设。然而,其中的自助样本集合依然不能全面反映测试指标的真实状态,在本质上还是“部分已知,部分未知”地实现对测试指标真实状态的认知。与原始N个数据所表征的“部分已知,部分未知”相比,前者的“已知部分”要远远地多于后者,这也是自助抽样挖掘的目的和作用。
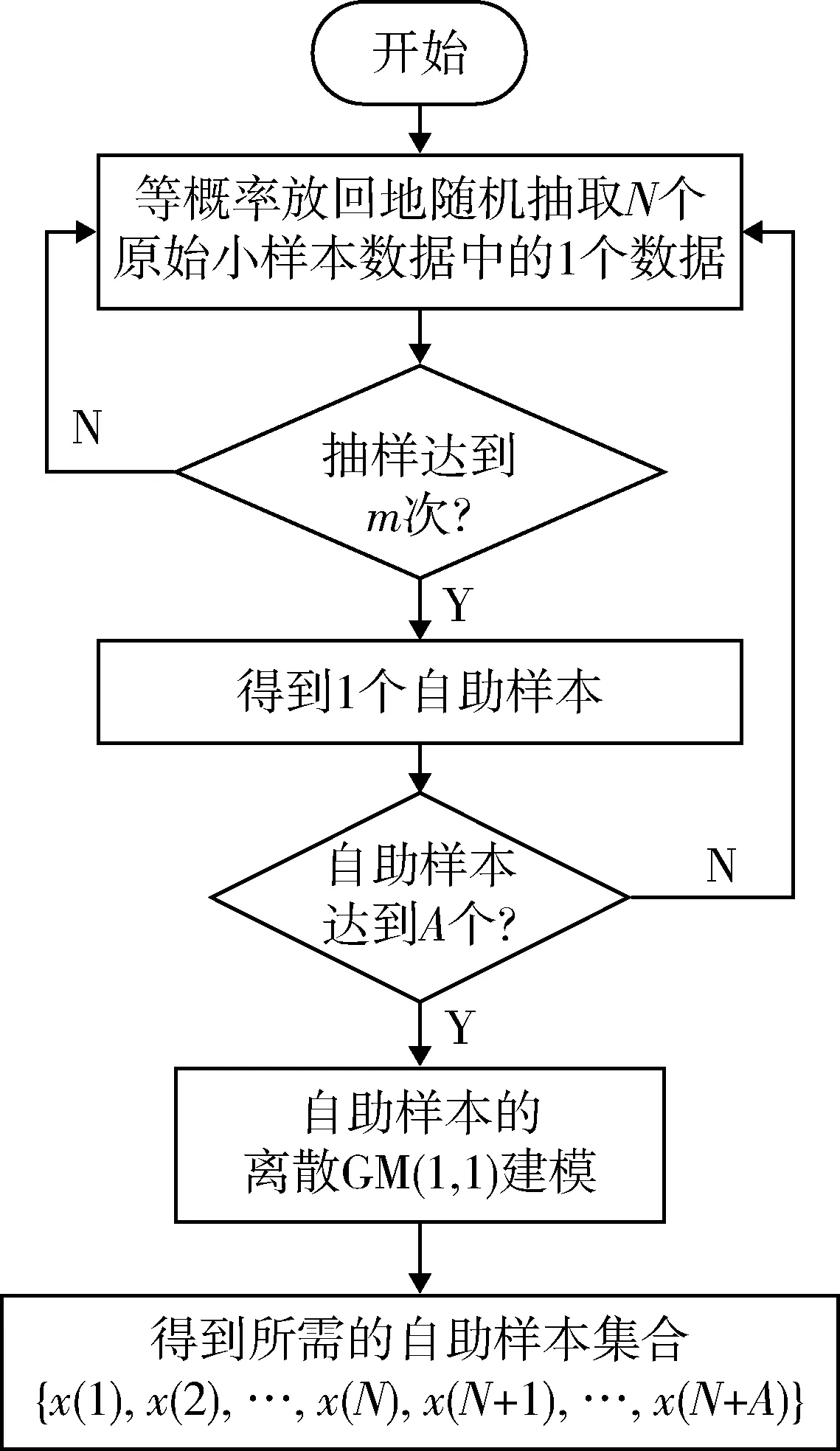
图1 小样本数据的自助抽样生成流程
2 基于未确知有理数的参数估计
对自助样本集合X′中N+A个数据的参数估计,若假设数据的分布特征,需要采用常规的统计方法进行点估计和参数估计,这就失去了自助抽样挖掘的意义,且数据分布特征的合理性和正确性难以验证。因此,不假设生成数据的概率分布规律,而直接引入未确知有理数方法进行参数估计。
2.1 未确知有理数的构造及优化
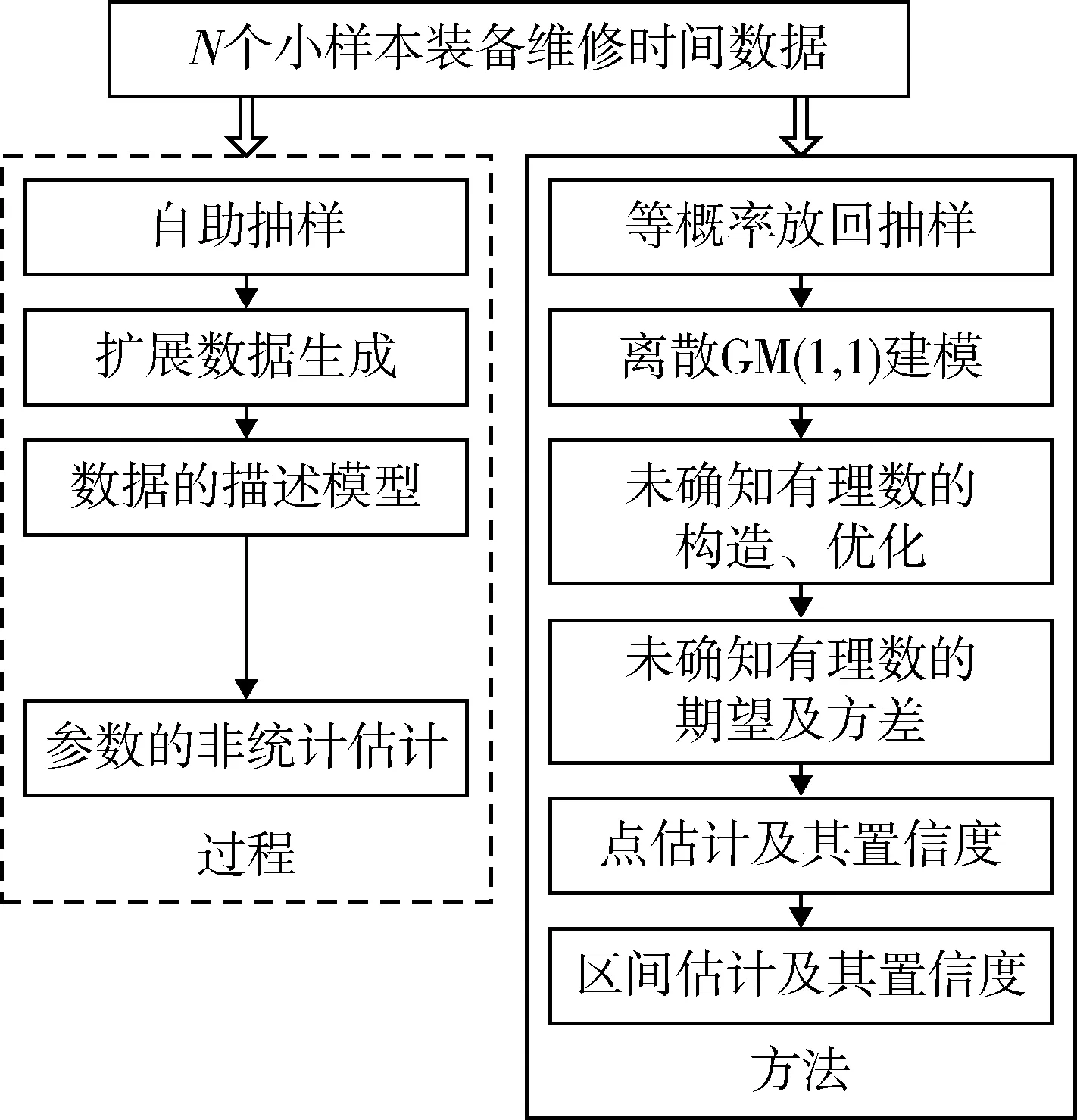
针对自助样本集合X′,构造一个h(h 1) 记 a=min{x(1),x(2),…,x(N), x(N+1),…,x(N+A)}; (11) b=max{x(1),x(2),…,x(N), x(N+1),…,x(N+A)}。 (12) 2) 以小区间的中间值xj(a≤xj≤b,j=1,2,…,h)为中心、λ为控制半径,确定一数据邻域,统计N+A个数据在该邻域出现的频率,则可得到可信度分布密度函数表达式 (13) 3) 大多数情况下,对区间[a,b]进行2h个等值划分,使得自助抽样数据值xj(j=1,2,…,h)的邻域控制半径均相等,则可得到其表达式为 (14) 其可信度αj则用自助抽样数据在xj为中心的控制邻域内出现的频率表示,即 (15) 4) 针对上述h阶未确知有理数的可信度熵 (16) (17) 称该h*阶未确知有理数U为一阶未确知有理数,其数学期望 (18) 式中: 用方差D(U)来描述未确知有理数U到E(U)的离散程度,即 D(U)=E(U-E(U))2= (19) 于是,自助样本的点估计值为 (20) 其估计精度为 (21) 综合未确知有理数期望的可信度,则定义自助样本点估计的置信度 (22) 假设自助样本的分布特征,可以用区间估计法给出样本的取值范围。一般假设自助样本服从正态分布,常用标准正态分布上侧β分位点如表1所示。 表1 常用标准正态分布上侧β分位点表 给定置信水平1-β,从表1中查询u(β/2),则给定置信水平下置信区间半长度 (23) 针对自助抽样挖掘生成的N+A个数据,假设有q个数据位于上述置信区间之外,同时综合估计区间的置信水平,则定义自助样本在上述区间估计的置信度 (24) 需要注意置信水平和置信度2个概念的联系与区别。本文对装备维修时间的非统计估计分为自助抽样生成、参数描述和参数估计等过程,置信水平反映了正态分布假设条件下区间估计的可靠性,覆盖了参数估计过程;而点估计和区间估计的置信度则覆盖了装备维修时间的非统计估计全过程,置信水平对区间估计置信度有一定的贡献率。 基于离散GM(1,1)模型的自助抽样生成和未确知有理数的装备维修时间非统计估计,是在小样本自助抽样生成、参数描述与估计等过程中,应用离散GM(1,1)建模技术,基于未确知有理数的点估计和区间估计等方法论的一种分析方法,其过程和方法论框架如图2所示。 图2 装备维修时间的非统计估计模型的过程和方法论框架 为验证本文算法的有效性,采用GJB 2072—94《维修性试验与评定》[2]D1.5中的装备维修时间数据,即26,14,21,30,70,69,20,21,18,65,16,34,26,16,40,28,42,33,19,19,43,54,12,18,13,26,10,50,21,31,42,30,46,24,总计34个。将自助样本的非统计估计结果与原始34个数据样本的非统计估计结果、GJB2072-94建议估计模型的估计结果进行对比验证。 利用本文非统计估计算法对D1.5中34个装备维修时间原始数据进行处理,其最佳4阶未确知有理数为[[10,70],φ(x)],其中 对原始34个数据,每间隔2个数据取为自助抽样对象,抽样生成小样本数据;而取小样本数据的前10个作为验证数据,即26,30,20,65,26,28,19,54,13,50。对这10个小样本数据进行等概率可放回地随机抽样,重复抽取m=6次视为得到1个自助样本,总共需要得到A=20个自助样本。 分别针对这20个自助样本进行离散GM(1,1)建模,取每个模型的一步预测值,从而得到自助样本集合为X′={26,30,20,65,26,28,19,54,13,50,22.1,13.5,27.5,51.2,24.8,23.4,26.5,34.2,65.8,41.1,32.7,46.0,29.0,16.5,12.1,69.0,51.5,19.5,17.8,29.6}。上述自助样本的最大值为69.0,最小值为12.1。构造h阶未确知有理数,其对应的可信度熵如表2所示。 表2 不同阶数未确知有理数的可信度熵 由表2可以看出:可信度熵最大值为0.137 6,其对应的最优未确知有理数阶数h*=4,则本算例构造的4阶未确知有理数为[[12.1,69.0],φ(x)],其中 假设置信水平为0.95,则β=0.05,计算给定置信水平下的置信区间半长度ε=14.17,则得到装备维修时间的区间估计[18.79,47.13],这时有q=12个点位于上述区间之外,区间估计的置信度p2=57.0%。 本算例中,装备维修时间的概率分布和方差都是未知的。依据GJB2072—94《维修性试验与评定》[2]D2中试验B的估计模型,有: 结合4.1、4.2节可知:针对自助样本、原始数据样本,基于本文非统计估计算法的点估计和区间估计结果均较为接近,且估计置信度也很接近,说明基于离散GM(1,1)模型的样本数据挖掘生成方法有效可行。 结合4.1-4.3节,对原始34个数据样本和自助样本分别进行点估计及位于估计区间之外的点数比较,如表3、4所示。 表3 点估计比较 表4 估计区间之外的样本点数比较 由表3可知:与GJB2072—94[2]建议估计模型的估计结果相比,原始数据样本的非统计估计模型点估计相对误差为1.15%,自助样本估计相对误差为0.39%,这2个数据样本的点估计结果相对误差均较小,而自助样本的误差更小。 由表4可知:同一置信水平下,估计区间覆盖了数据样本的个数,说明本文提出的非统计估计模型要远远好于GJB2072—94[2]估计模型。 上述结果表明:本文提出的小样本装备平均修复时间非统计估计模型有效可行。 针对装备平均修复时间的小样本参数估计问题,提出了一种基于离散GM(1,1)模型和未确知有理数的新方法,构建了装备平均修复时间的点估计和区间估计模型,并与GJB2072—94建议的估计模型进行对比,验证了其有效性。
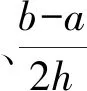
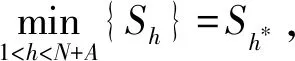
2.2 基于未确知有理数的点估计
2.3 基于未确知有理数的区间估计

3 非统计估计模型的过程和方法框架
4 装备平均修复时间的非统计估计算例
4.1 原始数据非统计估计结果
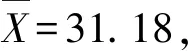
4.2 自助样本的非统计估计结果

4.3 GJB2072—94建议模型的估计结果
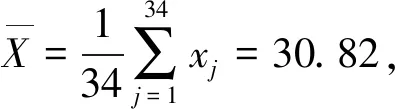
4.4 对比分析


5 结论
