声学回波统计的鱼群密度评估方法∗

梁 镜 许 枫 张 纯 马龙双

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

渔业资源声学评估由于具有快捷方便、可持续观测且不危害生物资源等优点，受到了广泛关注[1−5]。近几十年，除传统的回波积分、回波计数[6−7]评估方法外，学者们提出了诸如多频评估法[8]、基于回波峰值分布反演的方法[9−12]及回波统计评估法[13−17]等。其中，回波积分法是目前应用最为广泛的方法，该方法原理简单，但应用中需要准确计算鱼群回波的声能量，且需要鱼群中个体鱼的平均目标强度先验知识或拖网渔获数据辅助[6,18−19]。由于鱼类活动的随机性，同一尾鱼，在不同测量时刻，其目标强度测量值波动范围可达20 dB以上。而根据经典的回波积分方程，当鱼群回波目标强度测量误差为3 dB时，回波积分法鱼群密度评估结果相对误差就可达到100%[6]。因此，受声呐系统参数误差和鱼群中个体鱼的平均目标强度先验知识误差的影响，回波积分法的鱼群密度评估结果误差往往较大。与回波积分法相比，回波统计评估方法具有无需声呐回波信号绝对量(因而可避免声呐系统参数误差的干扰)与鱼群中个体鱼的平均目标强度先验知识的优点[15−16]，因而具有很好的发展前景。

在回波统计方法进行鱼群密度评估应用的有效性问题上，Weintroub[15]将该方法获得的5 组鱼群密度评估结果与传统的回波积分法评估结果进行了对比分析，发现两种方法下评估结果的线性相关系数高达0.98，但受鱼群密度分布不均匀导致的回波统计方法评估误差和回波积分法评估误差影响，回波统计方法的评估结果整体偏小。Denbigh等[16]提出根据回波信号强度的分布进行分区测量的方法，有效降低了鱼群密度分布不均匀性对回波统计方法评估结果的干扰，但由于可用于对比的不同鱼群密度分组数据较少和回波积分法评估误差大，Denbigh 等认为其处理结果不足以证明该评估方法的有效性。两者的研究中，评估方法模型参数均为经验假设估计值，无实测结果；采用的是走航调查数据，而由于实际水域鱼群分布的复杂性和走航调查对测量区域“一扫而过”的特点，可用于对比分析的不同鱼群密度分组和可用于统计计算的样本数据比较少。

针对以上情况，本文通过控制发射信号脉冲宽度和个体鱼回波检测程序设计，完成了对该统计方法模型参数的实际测量；在实验数据预处理上，提出了一种基于能量阈值的数据筛选方法，以减小鱼群分布的非均匀性导致的统计评估结果误差；在评估方法上，用“线性原则”模型代替常规的回波积分方程，避免了声呐系统误差带来的评估结果偏差。另外，针对走航调查中可能存在的统计样本数据偏少导致回波统计方法评估结果偏差的问题，对回波统计评估方法中样本数据的抽样方法进行了改进，有效提高了样本量偏少情况下该方法鱼群密度评估的精确度。本文利用仿真与实验结合的方式对该评估方法的有效性和样本数据抽样改进方法的性能进行了分析。

1 理论与方法

1.1 回波统计鱼群密度评估方法

对于声呐波束覆盖的某一观测微元(如图1所示)，假设t时刻微元内有N尾鱼对回波有贡献，忽略二次及以上散射，则该微元t时刻鱼群回波幅度AN可表示为

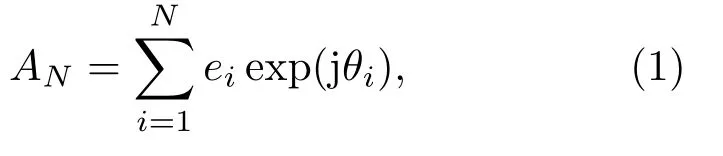
其中，ei为第i尾鱼的回波幅度，θi为由第i尾鱼的位置和散射决定的等效相位。有ei=aibici，其中ai是由该个体鱼本身的散射强度及姿态决定的后向散射幅度，bi是由声呐系统波束响应函数及抽样时刻该个体鱼在波束中的位置决定的波束响应值，ci与回波脉冲包络的波形有关[16]，三者之间是相互独立的。对应的回波信号强度IN可表示为

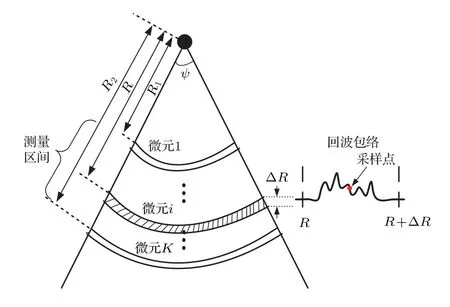
图1 微元与抽样示意图Fig.1 Diagram of resolution cell and data sampling

可以推导得到[16]

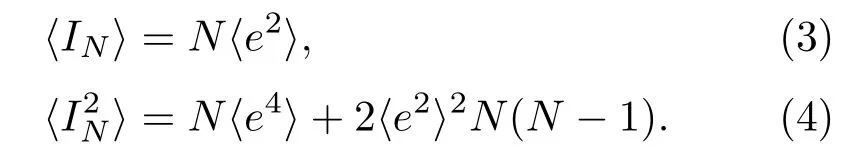
一般可以假设鱼群在测量区间随机游动过程中，在某点出现的概率服从Poisson 分布[14−17]，则微元中鱼的数量N服从Poisson 分布，其均值满足

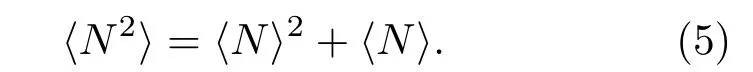
联立公式(3)∼(5)，可以推导得到微元回波信号强度统计特征量与微元中鱼的平均数量满足

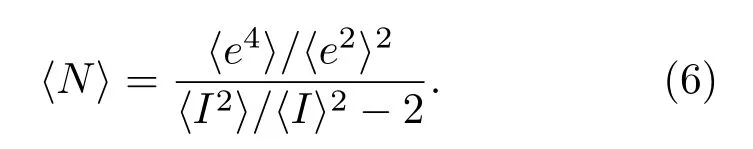
由于ei=aibici，且ai、bi、ci相互独立，因此满足

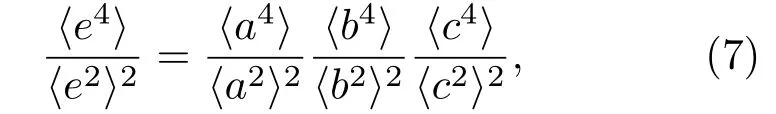
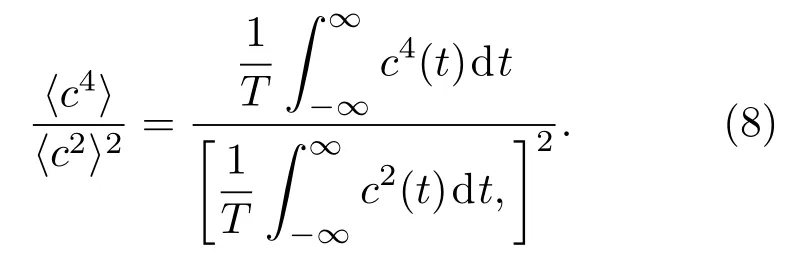
从公式(6)可以看出，该回波统计评估方法的参数与个体鱼回波幅度的归一化分布有关，而与个体鱼的目标强度无关。由于鱼类活动的随机性，个体鱼回波幅度的变化很大，但其归一化分布比较稳定，一般可以用Rayleigh 分布或Rician 分布进行拟合[15−16,20]。另外，由于最终统计量为归一化量因此，I可以是信号的相对强度，即公式(1)中回声信号的幅度可以为换能器输出的原始电压信号的幅度，而不必是真实的声压幅度，从而可以避免声源级、换能器接收灵敏度等参数误差对评估结果的影响。因此，与回波积分法相比，该方法既可以避免声呐工作参数误差对鱼群密度评估的影响，又具有无需鱼群中个体鱼的平均目标强度先验知识的优点。而利用公式(6)，联立声呐参数计算微元的体积，便能实现对鱼群密度的计算。

1.2 统计样本数据抽样方法改进

文献[14–16]的研究指出，该评估方法相对误差与微元值及统计的样本量M满足

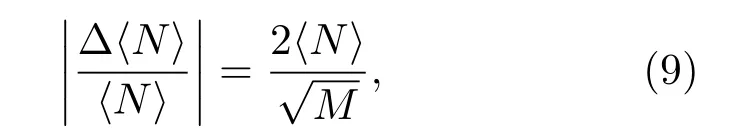
以往研究中一般以微元中间时刻回波信号的包络幅度作为该微元的唯一抽样值[14−16]，如图1所示。为方便表达，本文将该方法记为“单微元单样值(Single cell single sample, SCSS)”抽样方法。注意到由于微元中鱼的位置的随机性，以微元回波包络任意时刻t1或t2的幅度作为微元的抽样值是等效的，因此我们提出在微元中间部位等间隔抽取多个样本的抽样方法，即单微元多样值(Single cell multiple sample, SCMS)的方法。与SCSS 方法相比，微元数量相同条件下，SCMS等效于增加了统计样本量。

2 实验数据与处理方法

2.1 实验概况

网箱鱼群测量实验于2017年11月在黄海日照海域的海上平台完成，图2为实验安装简图。为便于控制鱼群活动范围和鱼群密度，实验选用的网箱体积较小，长、宽、高分别为2 m、2 m和5 m。网箱底部由直径30 mm 的PVC 管作支撑骨架，网衣为直径1 mm 左右、网孔2 cm 左右的尼龙线编织网片。网箱通过底部配重，从平台空隙处悬挂入海。换能器固定安装在网箱中央，距离水面0.5 m，照射方向朝下，其主瓣−3 dB 开角约10◦，发射信号为120 kHz的CW 脉冲信号，脉宽为τ= 0.1 ms。实验对象为长度15 cm∼20 cm的黑鲷鱼。实验过程中首先对空网箱进行了测量，发现除网箱底部外，其他部位几乎无回波，而网箱底部实际距离声呐约4 m，海底距离声呐约8 m，与网箱内鱼群的回波在时域上是可分的。实验测量了多组不同鱼群数量条件下的鱼群回波数据，其中网箱中鱼的数量最少为6 尾，最多为48 尾。考虑到测量过程中鱼群的集群分布特性，这些数据对应的网箱中鱼群的密度变化范围从不足1 尾每立方米，到最高约十尾每立方米，能较好地反映自然水域条件下鱼群的密度。

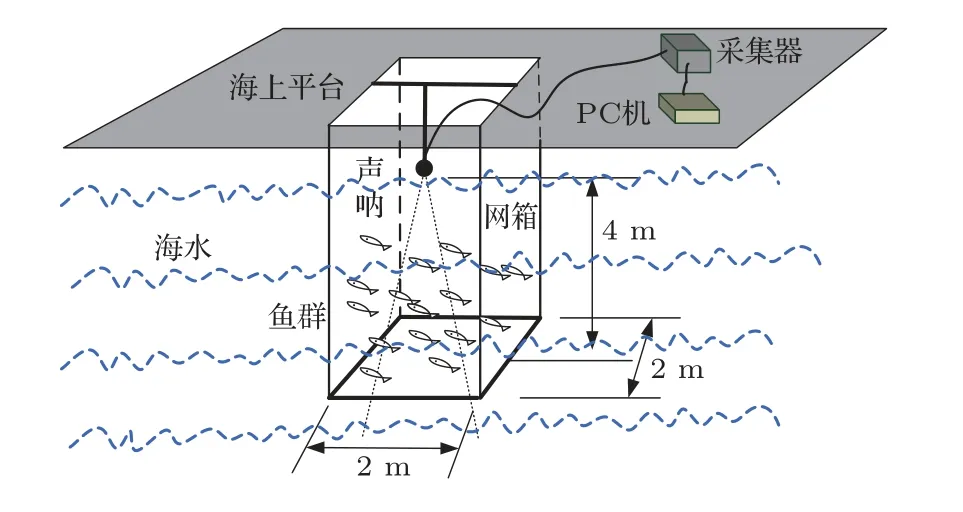
图2 网箱鱼群测量实验示意图Fig.2 Diagram of caged fish measurement experiments

2.2 个体鱼回波提取与模型参数计算

鱼群在网箱中自由游动，当某个体鱼远离其他鱼时，其回波在时域波形上与其他鱼的回波不重叠，此时便能从鱼群回波中提取出该个体鱼的回波。根据MacLennan 的经典文献[21]，可以利用以下准则对个体鱼回波进行判断：(1)目标波形长度T与发射信号脉冲宽度τ相近；(2)目标包络波形光滑。考虑目标回波脉冲展宽的特点，个体鱼回波波形宽度T要大于τ，但由于鱼体散射结构的复杂性以及鱼群活动的随机性，鱼群中不同大小或游动姿态的个体鱼回波的脉冲展宽略有不同。由于是从自由游动状态的鱼群回波中提取个体鱼回波，程序设计中，当目标波形长度T设置得太大时，容易把鱼群回波中脉冲展宽较小的重叠的回波错选为个体鱼回波；而当T设置得太小时，则容易漏选脉冲展宽较大的个体鱼回波。数据处理中，根据实测回波的特点和程序提取个体鱼回波的效果，在“错选”与“漏选”之间折中，最终选择了τT1.5τ作为本实验条件下个体鱼波形的有效长度，并以包络波形有且仅有一个极值点作为包络波形光滑的依据。图3为个体鱼回波的提取示例，可以看出该算法能较好地实现个体鱼回波的提取。利用该算法从鱼群实验回波数据中，共提取了2367例个体鱼回波样本。

对于波束中自由游动状态下的个体鱼，其回波的峰值Ai由鱼的散射幅度及其在波束中的位置决定，即Ai=aibi。图4给出了提取到的2367 例个体鱼样本的回波峰值Ai的分布，可以看出其近似Rician 分布，这与Clay等[2]的测量结果一致。通过对这些个体鱼的回波幅值统计计算得为1.55。另外，由于自身结构的复杂性，个体鱼回波包络呈不规则形状，利用公式(8) 对提取的个体鱼回波计算得到为1.41，利用公式(7)可得利用该计算结果，可以确立本实验条件下回波统计评估方法的表达式为

图3 个体鱼回波提取效果示图Fig.3 Diagram of individual fish echo extract

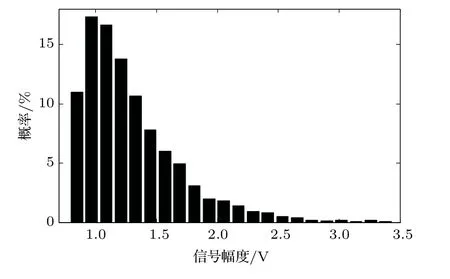
图4 个体鱼回波峰值概率分布图Fig.4 Individual fish echo peak PDF

2.3 数据筛选方法

鱼群在各微元分布的不均匀性会导致回波统计方法鱼群数量评估结果偏小[15]，例如有两个微元，对应的值分别为在鱼群均匀分布假设下，将两个微元回波抽样值作为等效的抽样值，对其进行统计平均，则可计算两微元特征量平均值

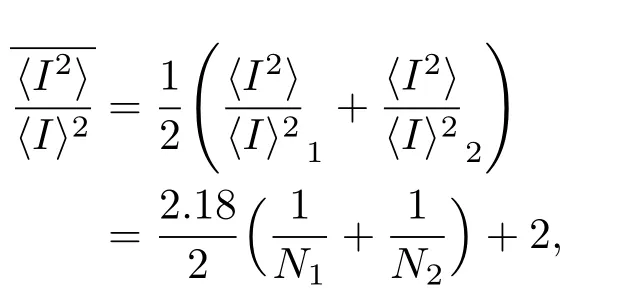
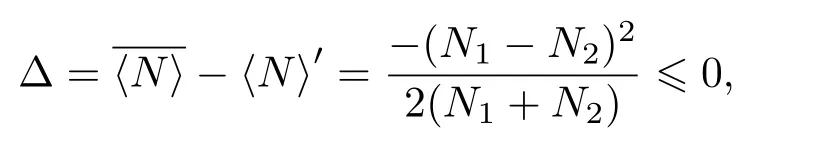
由此可见鱼群在各微元中分布的不均匀性会导致回波统计方法评估结果偏小。

实验每组数据约需半小时测量时间，测量过程中受网箱和外界环境干扰等因素的影响，鱼群虽然整体上集群分布于网箱中下层，但鱼群的活动比较活跃，而声呐波束照射范围仅为网箱中心的部分区域，因此测量过程中对回波有贡献的鱼的数量波动较大。为了减小鱼群分布的不均匀性带来的回波统计法评估误差，提出了一种基于能量阈值的鱼群回波数据筛选的方法：第一步，选择鱼群集中分布的水层作为目标区间；第二步，剔除目标区间内回波能量偏离平均回波能量比较大的数据。具体处理过程如下：(1)绘出每组鱼群回波数据的声图，根据回波声图中鱼群的分布情况，选择声图中鱼群分布集中的区间作为目标区间(如图5所示)。(2)计算目标区间内的回波信号的平均能量，并通过能量阈值设置选择信号能量在的回波数据帧作为模型计算的有效数据。需要指出的是，该能量阈值的选取不是绝对的，主要是考虑样本量大小与鱼群分布均匀性的一个折中结果。阈值范围越窄，筛选出的样本数据就越少，但对应目标区间内鱼数量的波动程度就越小；阈值范围越宽，则相反。通过以上筛选方法，本实验获得的8 组鱼群回波数据的样本量均在5000以上。

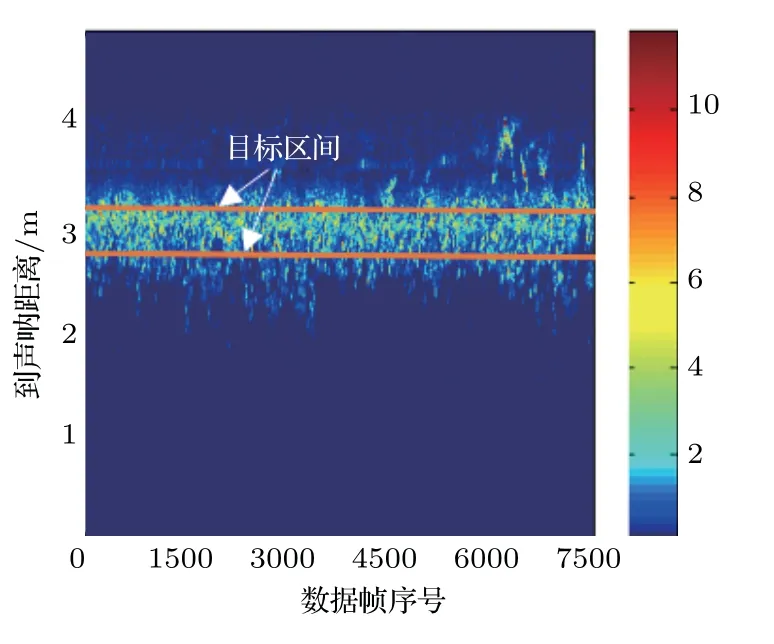
图5 鱼群回波声图与抽样区间Fig.5 Fish echogram and sample interval

2.4 回波积分方法

由于本文实验条件比较理想，从鱼群回波数据中提取到了大量鱼群中个体鱼的回波数据，获得了比较准确的鱼群中个体鱼的平均回波能量先验知识。结合该优势，直接采用鱼类资源评估中的“线性原则”作为回波积分法鱼群密度评估的表达式[6]，可表示为

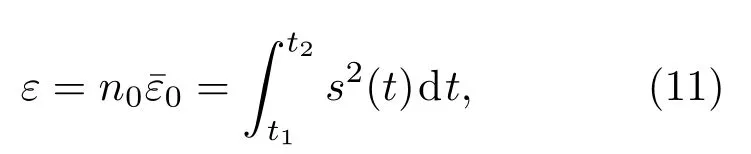
其中，ε为测量区间内鱼群回波总能量，n0为鱼的数量，为鱼群中个体鱼的平均回波能量，t1与t2分别为目标区间上下边界位置在时域回波信号上对应的时间点，s(t)为鱼群时域回波信号。该方法在以往的研究中得到了理论证明与实验验证[21−23]。实验过程中声呐参数始终保持不变，因此公式(11)中ε与可以是相对量，从而避免了声呐参数校准误差带来的回波积分法测量误差。另外，通过求2.2 节中个体鱼回波的平均回波能量，可得到本实验鱼群个体鱼的平均回波能量，从而确保了数据处理中回波积分法评估结果的准确性。

3 结果与分析

3.1 SCMS抽样方法效果验证

以2.2 节中提取的个体鱼的回波波形作为鱼群回波中个体鱼的波形样本，对两种抽样方法下回波统计方法评估效果进行仿真分析。方法如下：给定观测微元理论值后，首先利用目标区间内鱼群的数量服从Poisson 分布的假设，确定目标区间内各微元中个体鱼的数量Mi(i= 1,2,··· ,k)；然后从实测个体鱼波形样本中依次随机抽取Mi数量的个体鱼波形，并通过假设个体鱼在微元内均匀随机分布，实现鱼群回波波形的仿真；最后通过1000 次独立仿真实验取平均的方法，计算不同样本量(样本量=回波数据帧数乘以每帧微元个数)、不同微元值条件下，SCSS与SCMS(每个微元取3个抽样值)两种抽样方式下回波统计评估方法的平均相对误差仿真结果见表1，表中空白表示由于值太大而样本量偏少，导致计算结果中出现比理论值大百倍或者负值这样无效的结果。图6给出了该仿真方法下评估结果分布的一组示例，该图中微元理论值为3.5，采用的样本量为300。

表1 两种抽样方法下回波统计方法评估结果相对误差对比Table1 Mean relative error of the statistic model with the two sampling methods

利用实验实测数据，对两种抽样方式下回波统计方法评估效果进行进一步验证。方法是以2.3 节中筛选的8 组鱼群回波数据中总样本数最大的一组作为对象组(网箱中鱼总数为23 尾，测量样本数为7794)，然后通过随机抽样的方法，每次从对象组中抽取100 帧回波数据(每帧数据包含3 个微元，即总样本量为300)用于统计计算。利用该方法1000 次独立评估结果分布如图7所示。

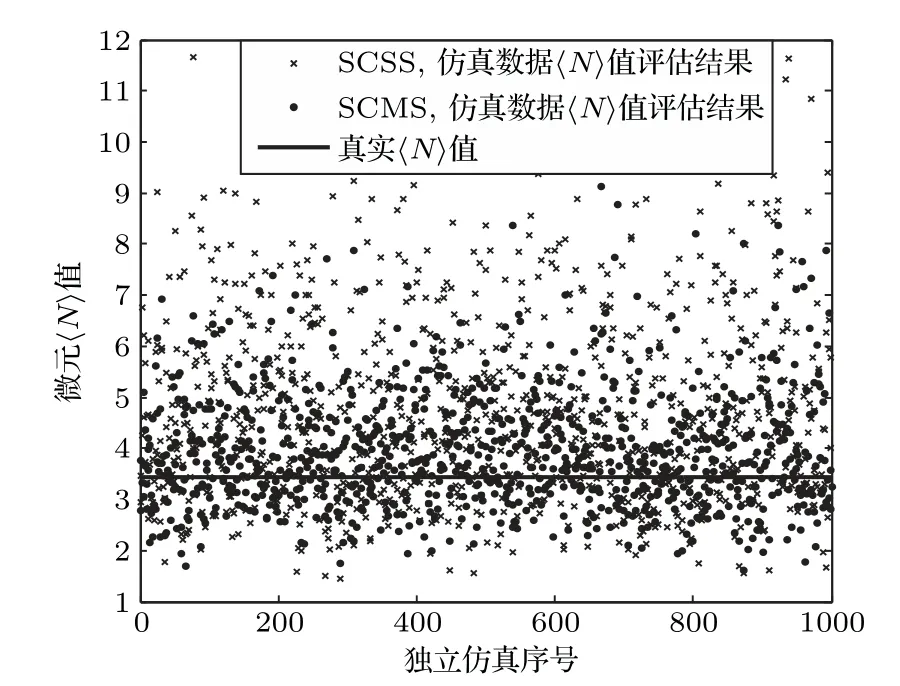
图6 仿真结果Fig.6 Simulation result

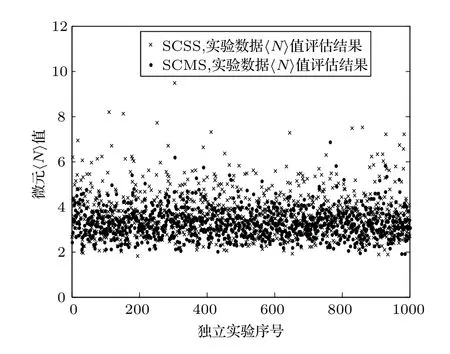
图7 实验结果Fig.7 Experiment result

从表1可以看出，两种抽样方式下回波统计方法评估结果相对误差基本符合随值的增大而增大，随样本量的增大而减小的规律。而从两种抽样方式下评估结果误差对比来看，对于一定的值，当统计样本量偏少时，SCMS抽样方式下评估结果较SCSS 具有更高的精确度，这一点在图6与图7中也有所反映。从图6和图7可以看出，样本量为300 时，SCSS 抽样方式下评估结果发散程度更大，而SCMS 方式下评估结果能更好地收敛于理论值附近。并且值越大，SCMS相较于SCSS的优势就越明显。但也注意到表1中=1时，在样本量充足的条件下，随着样本量的增加，出现了SCMS评估误差反而增大的情况，这可能是因为SCMS 在等效于增加样本的同时，也等效于增加了鱼群在各微元分布的不均匀性，从而导致评估结果偏小。因此，SCMS 抽样方式更适用于微元值大而样本量偏少的情况，此时由于样本量偏少导致的评估结果的不稳定性和偏差要大于由于SCMS 增加的不均匀性带来的偏差。

3.2 鱼群密度评估结果与分析

实验测量了8 组鱼总数量不同条件下的网箱鱼群回波数据，每组数据经能量阈值方法筛选后的样本量均在5000以上。分别利用回波统计鱼群数量评估方法(公式(10))和回波积分法(公式(11))对这8组鱼群回波数据进行评估，结果如图8所示。由于网箱中鱼总数为48 时，样本量约为5400，此时测量区间回波积分法评估结果值约为11，该鱼群密度条件已超出本实验条件下该统计评估方法的测量上限，其计算结果出现了无效值，因此图8中未给出该组测量结果。图8中最后一组数据，回波积分法值为9.3，统计模型评估结果明显偏大。对回波积分评估结果中6 的几组数据的线性相关系数进行了计算，发现两种方法计算结果线性相关系数高达0.99。利用最小二乘法对两种方法计算结果直线拟合，结果如图9所示。拟合直线表达式为其中为统计方法值评估结果为回波积分法值评估结果。可见对于多组不同鱼群密度条件下的鱼群回波数据，两种评估方法计算结果曲线具有很好的一致性，特别是微元值 6 时，两种评估方法计算结果基本相同，说明在该微元值条件下，回波统计方法能够有效地实现鱼群密度的评估。

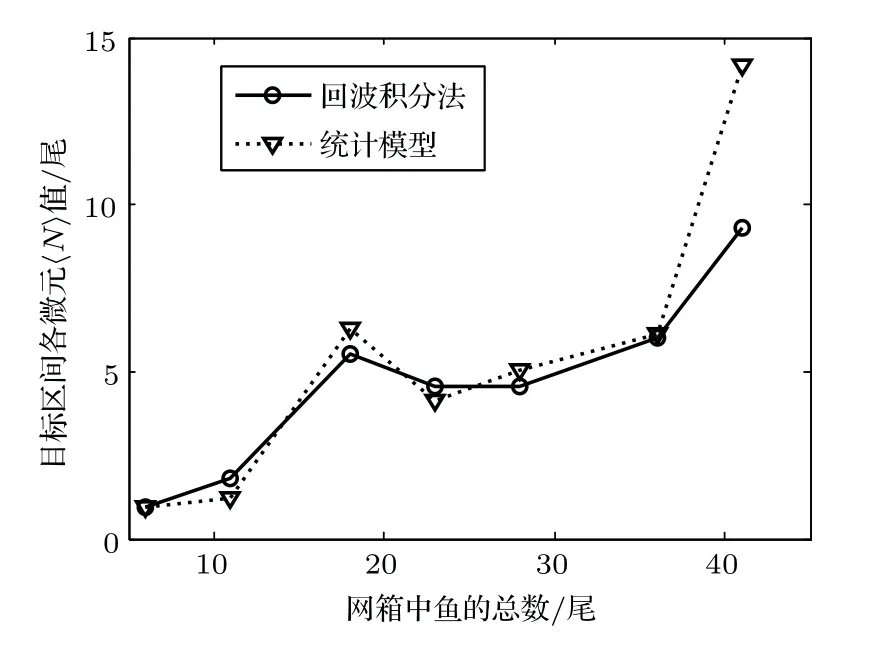
图8 两种方法评估结果对比Fig.8 Estimation result of the two methods

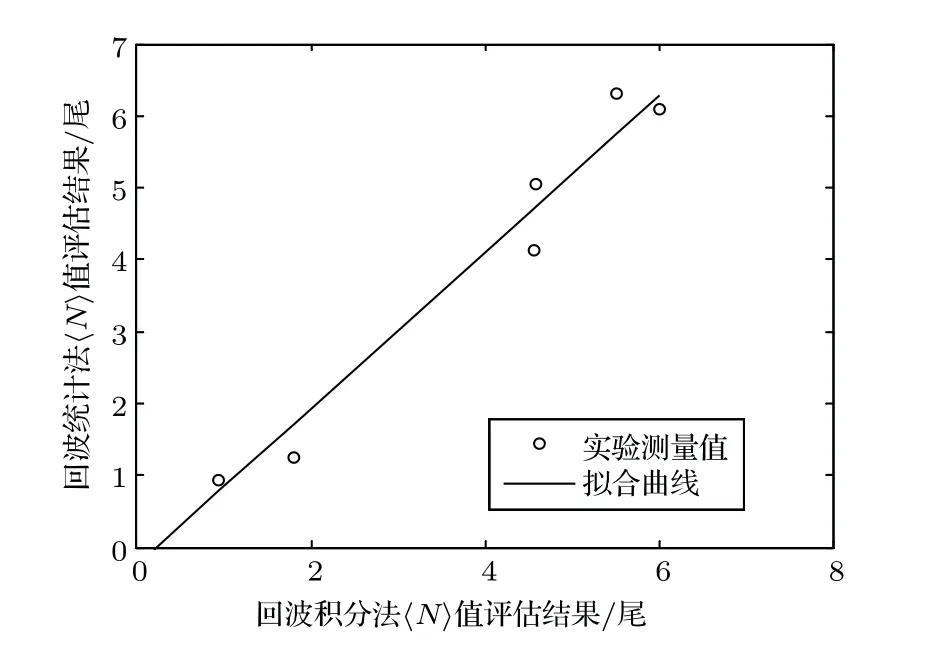
图9 两种方法评估结果线性拟合Fig.9 Linear fitting the result of the two methods

4 讨论与结论

本文对基于回波统计的鱼群密度评估方法进行了实验研究，并针对应用中该方法鱼群密度评估的误差问题，提出了一种基于能量阈值的数据筛选方法与SCMS 改进抽样方法。与以往研究相比，本文利用实验设计提取了大量个体鱼的回波数据，实现了回波统计鱼群密度评估法参数的实际测量计算；通过能量阈值数据筛选方法，获取了不同鱼群密度条件下分布比较均匀的鱼群回波数据。通过仿真和实验结果分析，可以得出以下结论：

(1)在统计样本充足的条件下，微元值越小，回波统计方法评估结果的精确度越高。本文实验条件下，当微元6时，回波统计方法与回波积分法评估结果基本一致。

(2)当微元值较大，或者统计样本量偏少，导致回波统计方法鱼群密度评估结果误差大时，利用本文提出的SCMS 抽样改进方法，能有效地提高回波数据的利用率，减小评估结果误差。